人教版数学九年级下册 27.2.1三角形相似判定3 学案
文档属性
| 名称 | 人教版数学九年级下册 27.2.1三角形相似判定3 学案 | 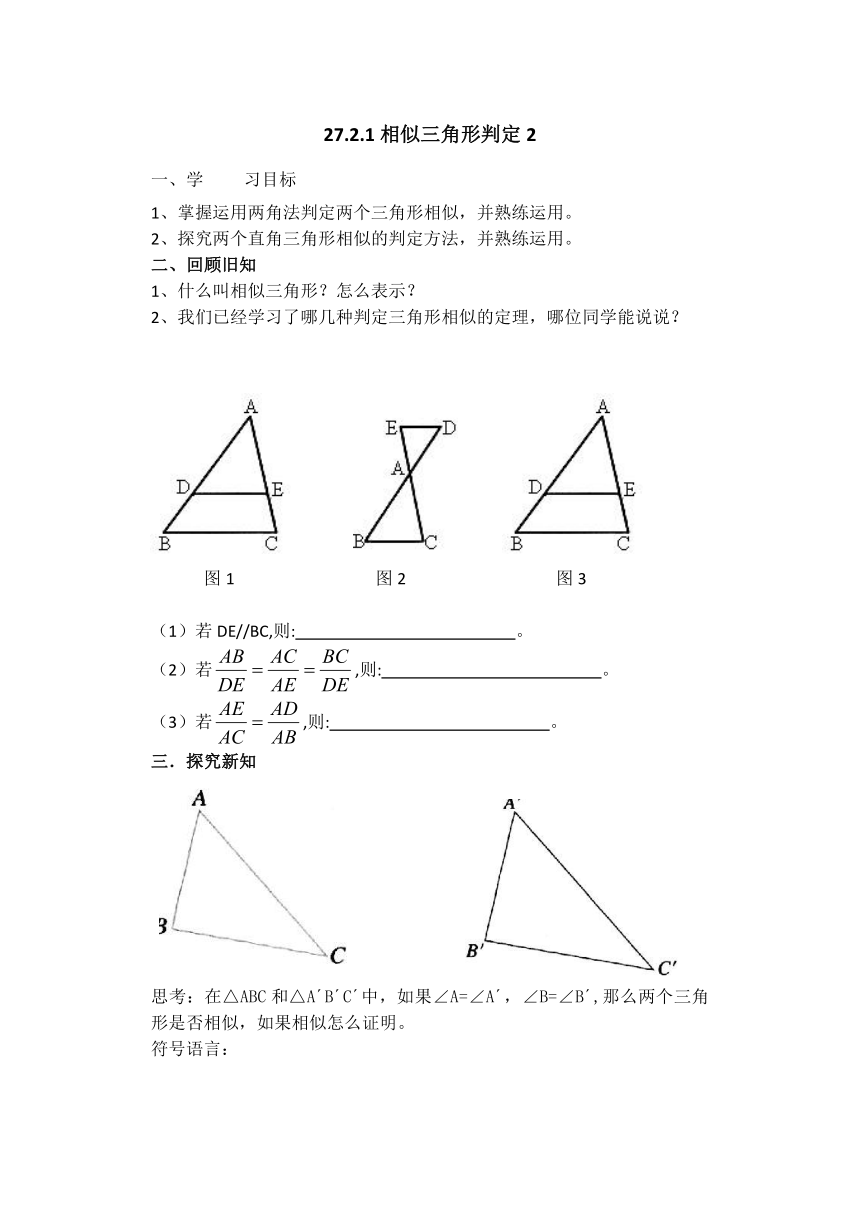 | |
| 格式 | zip | ||
| 文件大小 | 82.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 12:34:46 | ||
图片预览

文档简介
27.2.1相似三角形判定2
一、学习目标
1、掌握运用两角法判定两个三角形相似,并熟练运用。
2、探究两个直角三角形相似的判定方法,并熟练运用。
二、回顾旧知
1、什么叫相似三角形?怎么表示?
2、我们已经学习了哪几种判定三角形相似的定理,哪位同学能说说?
图1
图2
图3
若DE//BC,则:
。
若,则:
。
若,则:
。
探究新知
思考:在△ABC和△A?B?C?中,如果∠A=∠A?,∠B=∠B?,那么两个三角形是否相似,如果相似怎么证明。
符号语言:
跟踪检测1
在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=,AB=3,则BD=
1题
2题
已知:如图,△ABC中,∠A=36°,AB=AC,BD是角平分线。
(1)求证:(2)若AC=a,求AD。
自学指导
例2
如图在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,EDAB,垂足为D,求AD的长。
解:EDAB,
∠EDA=90°
又∠C=90°,∠A=∠A,
△ABC
∽
△AED
由三角形相似条件可知,如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似。
跟踪检测2
如图Rt△ABC,中,CD是斜边上的高,
求证Rt△ACD∽△ABC
△CBD∽△ABC
五.课堂小结
对桌交流本节课学习的判定方法
六、当堂达标
1、如图,在△ABC中,点D在线段BC上,∠BAC=∠ADC,AC=8,BC=16,则CD等于(
)
A
5
B
4
C
3
D
9
如图,D是△ABC的边AB上一点,若∠1=
,则△ADC∽△ACB,若∠2=
,则△ADC∽△ACB
已知:如图,在
Rt△ABC中,∠ACB=90°,CDAB于D
图中有哪两个三角形相似?
求证:
若AD=2,DB=8,求AC,BC,CD;
若AC=6,DB=9,求AD,CD,BC;
求证:
一、学习目标
1、掌握运用两角法判定两个三角形相似,并熟练运用。
2、探究两个直角三角形相似的判定方法,并熟练运用。
二、回顾旧知
1、什么叫相似三角形?怎么表示?
2、我们已经学习了哪几种判定三角形相似的定理,哪位同学能说说?
图1
图2
图3
若DE//BC,则:
。
若,则:
。
若,则:
。
探究新知
思考:在△ABC和△A?B?C?中,如果∠A=∠A?,∠B=∠B?,那么两个三角形是否相似,如果相似怎么证明。
符号语言:
跟踪检测1
在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=,AB=3,则BD=
1题
2题
已知:如图,△ABC中,∠A=36°,AB=AC,BD是角平分线。
(1)求证:(2)若AC=a,求AD。
自学指导
例2
如图在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,EDAB,垂足为D,求AD的长。
解:EDAB,
∠EDA=90°
又∠C=90°,∠A=∠A,
△ABC
∽
△AED
由三角形相似条件可知,如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似。
跟踪检测2
如图Rt△ABC,中,CD是斜边上的高,
求证Rt△ACD∽△ABC
△CBD∽△ABC
五.课堂小结
对桌交流本节课学习的判定方法
六、当堂达标
1、如图,在△ABC中,点D在线段BC上,∠BAC=∠ADC,AC=8,BC=16,则CD等于(
)
A
5
B
4
C
3
D
9
如图,D是△ABC的边AB上一点,若∠1=
,则△ADC∽△ACB,若∠2=
,则△ADC∽△ACB
已知:如图,在
Rt△ABC中,∠ACB=90°,CDAB于D
图中有哪两个三角形相似?
求证:
若AD=2,DB=8,求AC,BC,CD;
若AC=6,DB=9,求AD,CD,BC;
求证:
