人教版数学九年级下册 27.2.3相似三角形应用举例(1) 学案
文档属性
| 名称 | 人教版数学九年级下册 27.2.3相似三角形应用举例(1) 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 63.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 00:00:00 | ||
图片预览


文档简介
27.2.3
相似三角形应用举例(1)
一、学习目标:
1、能灵活建立相似三角形模型解决阳光下测物高问题。
2、能解决实际应用中的求河宽问题。
二、回顾旧知:
1、请同学们回顾相似三角形的判定方法有哪些?
2、常见的相似三角形模型有哪些?
三、探究新知一:阳光下测物高
例4
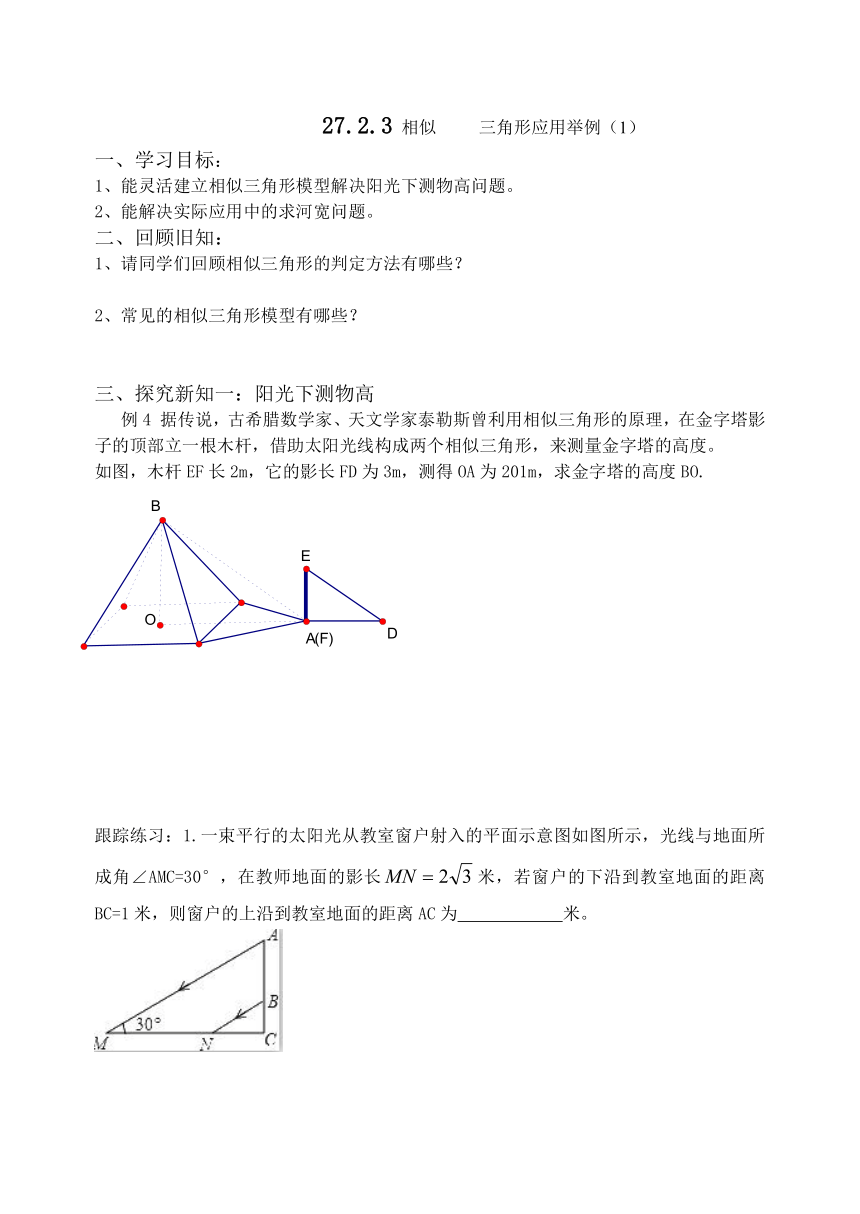
据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度。
如图,木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.
跟踪练习:1.一束平行的太阳光从教室窗户射入的平面示意图如图所示,光线与地面所成角∠AMC=30°,在教师地面的影长米,若窗户的下沿到教室地面的距离BC=1米,则窗户的上沿到教室地面的距离AC为
米。
2.
如图,在某一时刻测得1米长的竹竿竖直放置时影长1.2米,在同一时刻旗杆AB的影长不全落在水平地面上,有一部分落在楼房的墙上,他测得落在地面上的影长为BD=9.6米,留在墙上的影长CD=2米,则旗杆的高度。
探究新知二:求河宽
例5
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m
QR=60m,请根据这些数据
,求河的宽度PQ.
跟踪练习:1.如图,测得BD=120m,DC=60m,EC=50m,求河宽AB
拓展提升
如图,数学兴趣小组想测量电线杆AB的高度,他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量的CD=4m,BC=10m。CD与地面成30°角,且此时测得高1m的标杆的影长为2m,则电线杆的高度为
m(结果保留根号)。
方法归纳:
五、小结:解决阳光下测物高和河宽问题常用的相似三角形模型
当堂达标
如图,小明用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,竹竿与旗杆相距22m,则旗杆的高为(???
)?
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为?_________?米。
如图所示,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找到一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于点B,测出AB=8m,则池塘的宽DE为________.
A.32m
B.36m
C.48m
D.56m
相似三角形应用举例(1)
一、学习目标:
1、能灵活建立相似三角形模型解决阳光下测物高问题。
2、能解决实际应用中的求河宽问题。
二、回顾旧知:
1、请同学们回顾相似三角形的判定方法有哪些?
2、常见的相似三角形模型有哪些?
三、探究新知一:阳光下测物高
例4
据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度。
如图,木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.
跟踪练习:1.一束平行的太阳光从教室窗户射入的平面示意图如图所示,光线与地面所成角∠AMC=30°,在教师地面的影长米,若窗户的下沿到教室地面的距离BC=1米,则窗户的上沿到教室地面的距离AC为
米。
2.
如图,在某一时刻测得1米长的竹竿竖直放置时影长1.2米,在同一时刻旗杆AB的影长不全落在水平地面上,有一部分落在楼房的墙上,他测得落在地面上的影长为BD=9.6米,留在墙上的影长CD=2米,则旗杆的高度。
探究新知二:求河宽
例5
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m
QR=60m,请根据这些数据
,求河的宽度PQ.
跟踪练习:1.如图,测得BD=120m,DC=60m,EC=50m,求河宽AB
拓展提升
如图,数学兴趣小组想测量电线杆AB的高度,他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量的CD=4m,BC=10m。CD与地面成30°角,且此时测得高1m的标杆的影长为2m,则电线杆的高度为
m(结果保留根号)。
方法归纳:
五、小结:解决阳光下测物高和河宽问题常用的相似三角形模型
当堂达标
如图,小明用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,竹竿与旗杆相距22m,则旗杆的高为(???
)?
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为?_________?米。
如图所示,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找到一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于点B,测出AB=8m,则池塘的宽DE为________.
A.32m
B.36m
C.48m
D.56m
