小学数学西师大版六年级上册 阴影部分面积 教案
文档属性
| 名称 | 小学数学西师大版六年级上册 阴影部分面积 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 46.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-10 11:33:05 | ||
图片预览

文档简介
组合图形的周长和面积
一 割补法
割补法和分割法用于几何题之中。割补法就是把图形切开,把切下来的那部分移动到其他位置,使题目便于解答;分割法就是同样把图形切开,但是并不移动,使题目便于解答。
二 等积法
谓“等积法” ,是指某些几何问题中 ,可以通过面积相等关系 ,导出其它几何元素之间的关系 ,从而使问题得以解决
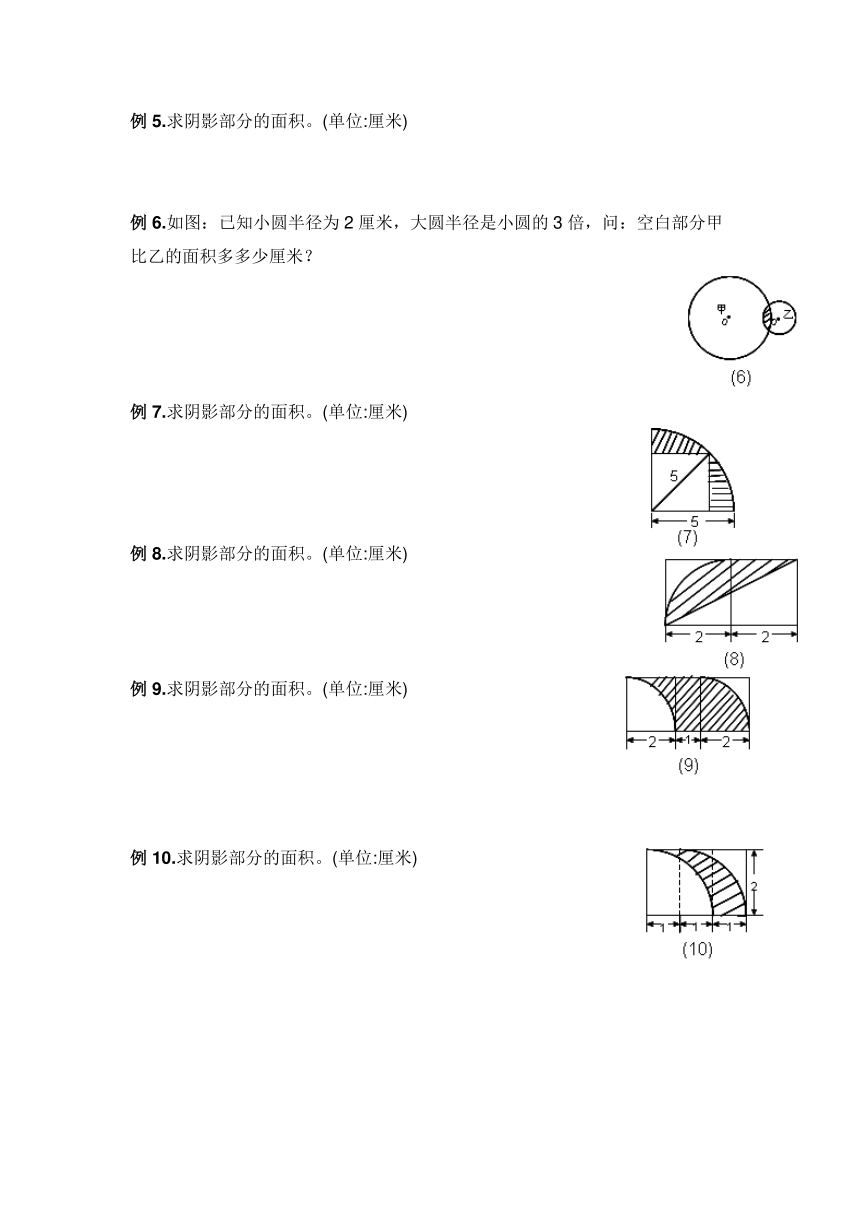
例1.求阴影部分的面积。(单位:厘米)
例2.正方形面积是7平方厘米,求阴影部分的面积。(单位:厘米)
例3.求图中阴影部分的面积。(单位:厘米)
例4.求阴影部分的面积。(单位:厘米)
例5.求阴影部分的面积。(单位:厘米)
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?
例7.求阴影部分的面积。(单位:厘米)
例8.求阴影部分的面积。(单位:厘米)
例9.求阴影部分的面积。(单位:厘米)
例10.求阴影部分的面积。(单位:厘米)
(注: 8、9、10三题是简单割、补或平移)
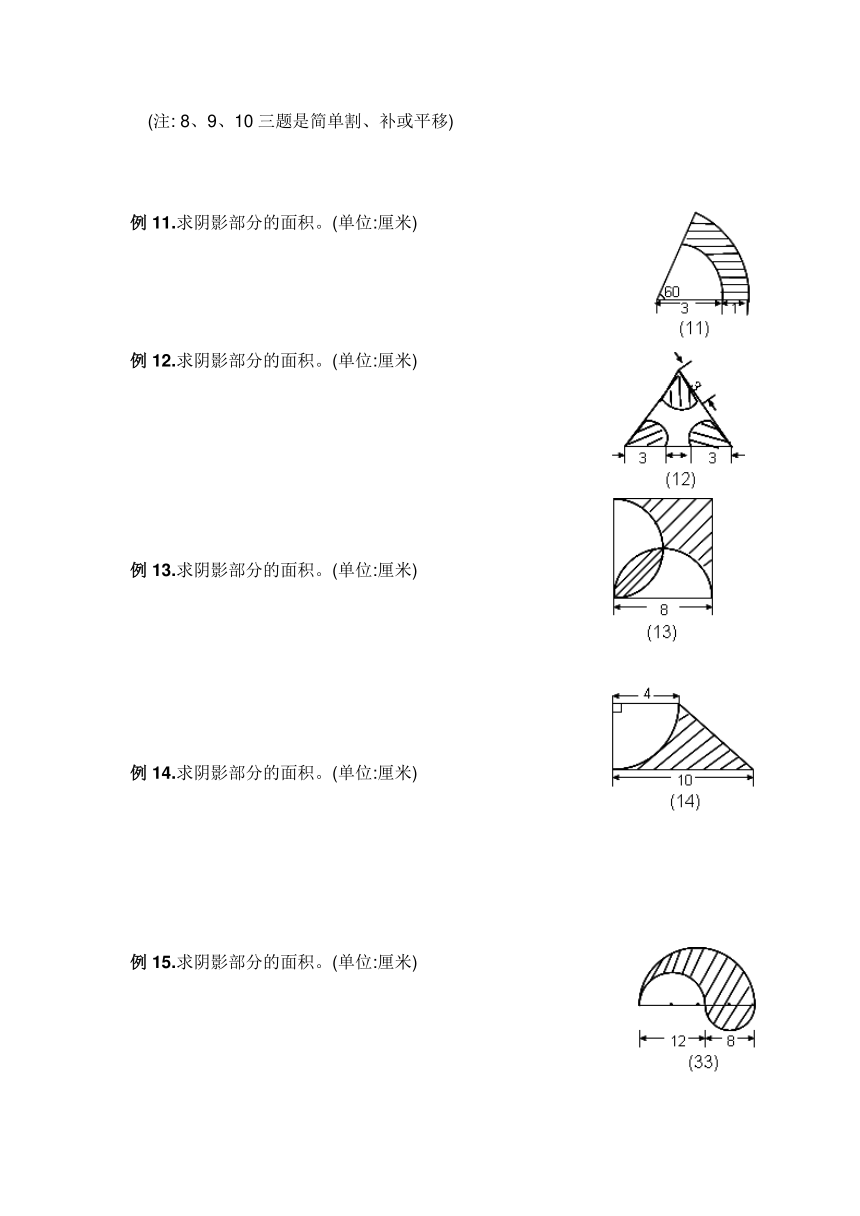
例11.求阴影部分的面积。(单位:厘米)
例12.求阴影部分的面积。(单位:厘米)
例13.求阴影部分的面积。(单位:厘米)
例14.求阴影部分的面积。(单位:厘米)
例15.求阴影部分的面积。(单位:厘米)
例16.图中圆的半径为5厘米,求阴影部分的面积。(单位:厘米)
例17.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例18.正方形边长为2厘米,求阴影部分的面积。
例19.图中四个圆的半径都是1厘米,求阴影部分的面积。
例20.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?
例21.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。求BC的长度。
练习
1.如图,大正方形的边长为6厘米,小正方形的边长为4厘米。求阴影部分的面积。
2.求阴影部分的面积。(单位:厘米)
3.如图,三角形OAB是等腰直角三角形,OBC是扇形,OB=5厘米,求阴影部分的面积。
4、
左图中,阴影部分的面积占总面积的
5、右图中三个阴影部分的面积相比,( )最大。 3
A、平行四边形 B、三角形
C、梯形
7 12 8
7 12 8
一 割补法
割补法和分割法用于几何题之中。割补法就是把图形切开,把切下来的那部分移动到其他位置,使题目便于解答;分割法就是同样把图形切开,但是并不移动,使题目便于解答。
二 等积法
谓“等积法” ,是指某些几何问题中 ,可以通过面积相等关系 ,导出其它几何元素之间的关系 ,从而使问题得以解决
例1.求阴影部分的面积。(单位:厘米)
例2.正方形面积是7平方厘米,求阴影部分的面积。(单位:厘米)
例3.求图中阴影部分的面积。(单位:厘米)
例4.求阴影部分的面积。(单位:厘米)
例5.求阴影部分的面积。(单位:厘米)
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?
例7.求阴影部分的面积。(单位:厘米)
例8.求阴影部分的面积。(单位:厘米)
例9.求阴影部分的面积。(单位:厘米)
例10.求阴影部分的面积。(单位:厘米)
(注: 8、9、10三题是简单割、补或平移)
例11.求阴影部分的面积。(单位:厘米)
例12.求阴影部分的面积。(单位:厘米)
例13.求阴影部分的面积。(单位:厘米)
例14.求阴影部分的面积。(单位:厘米)
例15.求阴影部分的面积。(单位:厘米)
例16.图中圆的半径为5厘米,求阴影部分的面积。(单位:厘米)
例17.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例18.正方形边长为2厘米,求阴影部分的面积。
例19.图中四个圆的半径都是1厘米,求阴影部分的面积。
例20.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?
例21.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。求BC的长度。
练习
1.如图,大正方形的边长为6厘米,小正方形的边长为4厘米。求阴影部分的面积。
2.求阴影部分的面积。(单位:厘米)
3.如图,三角形OAB是等腰直角三角形,OBC是扇形,OB=5厘米,求阴影部分的面积。
4、
左图中,阴影部分的面积占总面积的
5、右图中三个阴影部分的面积相比,( )最大。 3
A、平行四边形 B、三角形
C、梯形
7 12 8
7 12 8
