沪科版(2012)初中数学九年级下册 24.8 综合与实践:射门线路与最佳射门角 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 24.8 综合与实践:射门线路与最佳射门角 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 105.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 15:35:05 | ||
图片预览

文档简介
24.8综合与实践
教学设计
进球线路与最佳射门角
一、教学背景
(一)教材分析
本节课的内容为进球线路与最佳射门角,选自沪科版九年级数学下册第二十四章《圆》第八节的内容,要求学生能理解进球线路和最佳射门角存在关系,结合圆及相关知识,找到最佳射门角。本节内容是本章知识的升华和提高,是数学知识与现实生活的紧密联系。
(二)学情分析
学生已经学习了圆的知识,对圆周角、圆内角、圆外角的比较已经掌握,并有一定的生活经验。但本节内容比较抽象,将结合几何画板进行讲解分析,提高直观性。
二、教学目标
让学生理解能利用圆的知识分析进球路线与射门角度关系,通过观察分类、观察、思考进球路线与射门角度存在关系。通过不同进球路线的分析,结合圆周角的知识找到最佳射门角。让学生感受数学对现实生活的意义,体会分类讨论思想。培养学生积极参与和勇于探索的精神。
三、教学重点与难点
教学重点:理解进球路线和射门角关系。
教学难点:利用圆及相关知识找到最佳射门角。
四、教学方法分析及学习方法指导
多媒体教学,利用几何画板辅助理解,让学生通过观察、思考、讨论、交流结合圆的知识,找出最佳进球角。
五、教学过程
(一)导入新课
足球场上的顺口溜:冲向球门跑,越近就越好;
歪着球门跑,射点要选好!
足球运动已成为一种世界性的运动,也是我们大家喜欢欣赏的一种体育活动。在比赛的过程中,运动员在对方球门前不同的位置起脚射门对球门的威胁是不相同的。
设计意图:从生活中的实际问题入手,使学生认识到数学总是与现实问题密不可分,同时激发学生的学习热情。
(二)新授内容
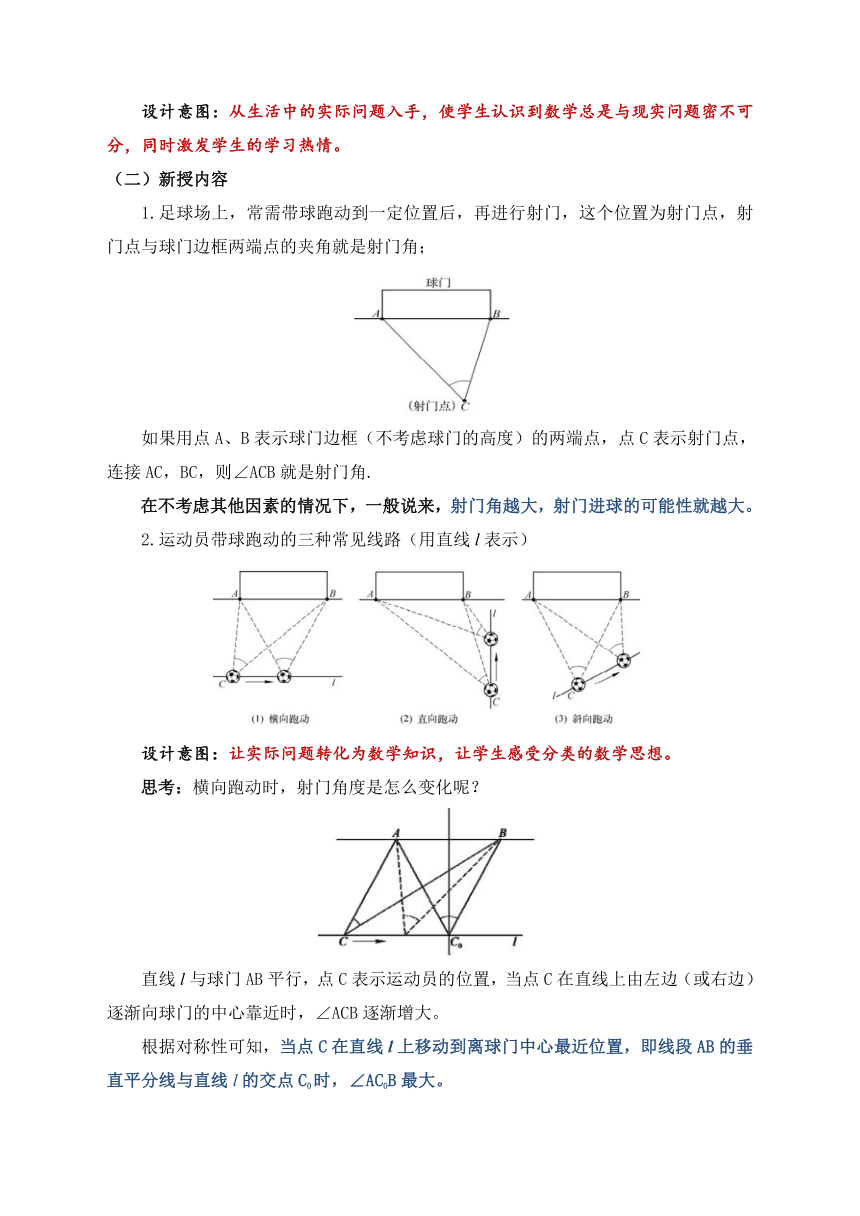
1.足球场上,常需带球跑动到一定位置后,再进行射门,这个位置为射门点,射门点与球门边框两端点的夹角就是射门角;
如果用点A、B表示球门边框(不考虑球门的高度)的两端点,点C表示射门点,连接AC,BC,则∠ACB就是射门角.
在不考虑其他因素的情况下,一般说来,射门角越大,射门进球的可能性就越大。
2.运动员带球跑动的三种常见线路(用直线l表示)
设计意图:让实际问题转化为数学知识,让学生感受分类的数学思想。
思考:横向跑动时,射门角度是怎么变化呢?
直线l与球门AB平行,点C表示运动员的位置,当点C在直线上由左边(或右边)逐渐向球门的中心靠近时,∠ACB逐渐增大。
根据对称性可知,当点C在直线l上移动到离球门中心最近位置,即线段AB的垂直平分线与直线l的交点C0时,∠AC0B最大。
思考:当直线l向上平移到直线l′时,射门角度又是怎么变化呢?
C0
→
C2,∠AC0B
→
∠AC2B,且∠AC2B﹥∠AC0B.
由此可见,当运动员沿直线l横向跑动时,他的位置离球门的中心越近,射门角度越大,离球门的中心最近(点C0)时,射门角最大,我们把点C0称为直线l上的最佳射门点,
∠AC0B
称为直线l上的最佳射门角.
最佳射门角的大小和直线l与AB的距离有关,由图可知,当直线l与AB的距离越近,最佳射门角越大,射门进球的可能就越大,这与我们的踢足球的经验相吻合.
通过上面的知识,我们可以得到这样的结论:
如果⊙O过点AB,而直线AB的同侧的三点C1、C0、C2,分别在⊙O外,⊙O上和⊙O内,则有:
∠AC1B﹤∠AC0B﹤∠AC2B
简单的说:在弦的同侧,同弦所对的圆外角α、圆周角β和圆内角θ的大小关系为:α
﹤
β
﹤
θ
设计意图:结合圆的知识,利用过三点作圆,对圆内角、圆周角、圆外角的大小比较,让实际问题转化为数学知识,让学生理解横向跑动时,射门角度增加,向前跑动时,射门角度最大
。
※当运动员直向跑动时,球门AB与直线l垂直,点C是运动员的位置。
(1)作出过A、B、C三点的圆,猜想当点C在直线l上移动时,直线l与该圆的位置关系;
(2)当直线l与该圆有怎样的位置关系时,∠ACB是直线l上的最佳射门角;
(3)已知AB=m,BD=n,当点C在直线l上的最佳射门点时,求CD的长;
(4)向左平移直线l到直线l′,观察直线l上的最佳射门角与直线l上的最佳射门角之间的大小关系,写出你的结论.
设计意图:结合圆的知识,利用过三点作圆,让实际问题转化为数学知识,当圆与直线l相切时,射门角度最大,并利用相似知识进行计算。让学生理解直向跑动时,何时射门角最大
。以及直线l靠近球门时,最佳射门角度变大。
(三)能力提升
当运动员直向跑动时,直线l垂直穿过球门AB,点C时运动员的位置.
(1)∠ACB的大小是怎么变化的?
(2)直线l上还有没有最佳射门点?说明你的理由.
设计意图:让学生自己主动思考,并结合几何图形理解直线l垂直穿过球门AB时,射门角度增加。
(四)课时小结:
对自己说,你有什么收获?
对同学说,你有什么提示?
对老师说,你还有什么困惑?
设计意图:小结宗旨在于让学生反思自己的学习过程,总结归纳,提高学生的数学素养。
(五)作业
1.对运动员斜向跑动时进行相关探究,或自选一个问题进行探究.
2.与同学合作,将探究的结果写成小论文,并检验你得到的结论是否与足球运动的实际相符合.
设计意图:布置作业的目的在于让学生巩固自己所学的知识,能对新知进行灵活运用。让数学知识与实际想联系,激发学生学习兴趣。
六、板书设计
七、教案反思
教学设计
进球线路与最佳射门角
一、教学背景
(一)教材分析
本节课的内容为进球线路与最佳射门角,选自沪科版九年级数学下册第二十四章《圆》第八节的内容,要求学生能理解进球线路和最佳射门角存在关系,结合圆及相关知识,找到最佳射门角。本节内容是本章知识的升华和提高,是数学知识与现实生活的紧密联系。
(二)学情分析
学生已经学习了圆的知识,对圆周角、圆内角、圆外角的比较已经掌握,并有一定的生活经验。但本节内容比较抽象,将结合几何画板进行讲解分析,提高直观性。
二、教学目标
让学生理解能利用圆的知识分析进球路线与射门角度关系,通过观察分类、观察、思考进球路线与射门角度存在关系。通过不同进球路线的分析,结合圆周角的知识找到最佳射门角。让学生感受数学对现实生活的意义,体会分类讨论思想。培养学生积极参与和勇于探索的精神。
三、教学重点与难点
教学重点:理解进球路线和射门角关系。
教学难点:利用圆及相关知识找到最佳射门角。
四、教学方法分析及学习方法指导
多媒体教学,利用几何画板辅助理解,让学生通过观察、思考、讨论、交流结合圆的知识,找出最佳进球角。
五、教学过程
(一)导入新课
足球场上的顺口溜:冲向球门跑,越近就越好;
歪着球门跑,射点要选好!
足球运动已成为一种世界性的运动,也是我们大家喜欢欣赏的一种体育活动。在比赛的过程中,运动员在对方球门前不同的位置起脚射门对球门的威胁是不相同的。
设计意图:从生活中的实际问题入手,使学生认识到数学总是与现实问题密不可分,同时激发学生的学习热情。
(二)新授内容
1.足球场上,常需带球跑动到一定位置后,再进行射门,这个位置为射门点,射门点与球门边框两端点的夹角就是射门角;
如果用点A、B表示球门边框(不考虑球门的高度)的两端点,点C表示射门点,连接AC,BC,则∠ACB就是射门角.
在不考虑其他因素的情况下,一般说来,射门角越大,射门进球的可能性就越大。
2.运动员带球跑动的三种常见线路(用直线l表示)
设计意图:让实际问题转化为数学知识,让学生感受分类的数学思想。
思考:横向跑动时,射门角度是怎么变化呢?
直线l与球门AB平行,点C表示运动员的位置,当点C在直线上由左边(或右边)逐渐向球门的中心靠近时,∠ACB逐渐增大。
根据对称性可知,当点C在直线l上移动到离球门中心最近位置,即线段AB的垂直平分线与直线l的交点C0时,∠AC0B最大。
思考:当直线l向上平移到直线l′时,射门角度又是怎么变化呢?
C0
→
C2,∠AC0B
→
∠AC2B,且∠AC2B﹥∠AC0B.
由此可见,当运动员沿直线l横向跑动时,他的位置离球门的中心越近,射门角度越大,离球门的中心最近(点C0)时,射门角最大,我们把点C0称为直线l上的最佳射门点,
∠AC0B
称为直线l上的最佳射门角.
最佳射门角的大小和直线l与AB的距离有关,由图可知,当直线l与AB的距离越近,最佳射门角越大,射门进球的可能就越大,这与我们的踢足球的经验相吻合.
通过上面的知识,我们可以得到这样的结论:
如果⊙O过点AB,而直线AB的同侧的三点C1、C0、C2,分别在⊙O外,⊙O上和⊙O内,则有:
∠AC1B﹤∠AC0B﹤∠AC2B
简单的说:在弦的同侧,同弦所对的圆外角α、圆周角β和圆内角θ的大小关系为:α
﹤
β
﹤
θ
设计意图:结合圆的知识,利用过三点作圆,对圆内角、圆周角、圆外角的大小比较,让实际问题转化为数学知识,让学生理解横向跑动时,射门角度增加,向前跑动时,射门角度最大
。
※当运动员直向跑动时,球门AB与直线l垂直,点C是运动员的位置。
(1)作出过A、B、C三点的圆,猜想当点C在直线l上移动时,直线l与该圆的位置关系;
(2)当直线l与该圆有怎样的位置关系时,∠ACB是直线l上的最佳射门角;
(3)已知AB=m,BD=n,当点C在直线l上的最佳射门点时,求CD的长;
(4)向左平移直线l到直线l′,观察直线l上的最佳射门角与直线l上的最佳射门角之间的大小关系,写出你的结论.
设计意图:结合圆的知识,利用过三点作圆,让实际问题转化为数学知识,当圆与直线l相切时,射门角度最大,并利用相似知识进行计算。让学生理解直向跑动时,何时射门角最大
。以及直线l靠近球门时,最佳射门角度变大。
(三)能力提升
当运动员直向跑动时,直线l垂直穿过球门AB,点C时运动员的位置.
(1)∠ACB的大小是怎么变化的?
(2)直线l上还有没有最佳射门点?说明你的理由.
设计意图:让学生自己主动思考,并结合几何图形理解直线l垂直穿过球门AB时,射门角度增加。
(四)课时小结:
对自己说,你有什么收获?
对同学说,你有什么提示?
对老师说,你还有什么困惑?
设计意图:小结宗旨在于让学生反思自己的学习过程,总结归纳,提高学生的数学素养。
(五)作业
1.对运动员斜向跑动时进行相关探究,或自选一个问题进行探究.
2.与同学合作,将探究的结果写成小论文,并检验你得到的结论是否与足球运动的实际相符合.
设计意图:布置作业的目的在于让学生巩固自己所学的知识,能对新知进行灵活运用。让数学知识与实际想联系,激发学生学习兴趣。
六、板书设计
七、教案反思
