直线与圆的位置关系
图片预览



文档简介
(共19张PPT)
25.5 直线和圆的位置关系(2)
-----切线的判定定理和性质定理
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
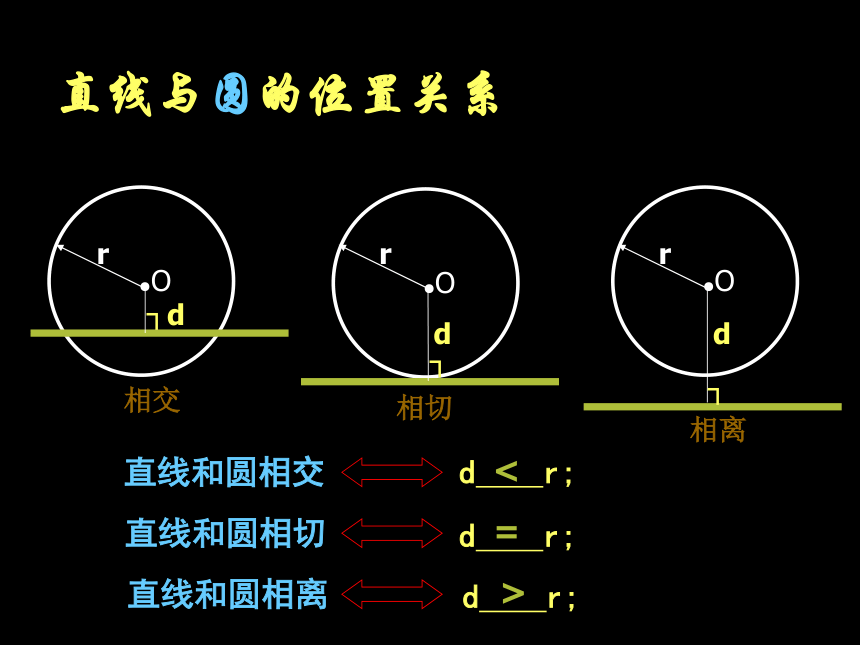
直线和圆相切
d r;
d r;
直线和圆相交
直线和圆相离
d r;
直线与圆的位置关系
<
=
>
目前,我们学过几种方法可以判定直线与圆相切?
1.看直线与圆交点的个数(有且只有一个)。
2.比较圆心到直线的距离与半径的大小。(d=r)
.
O
A
L
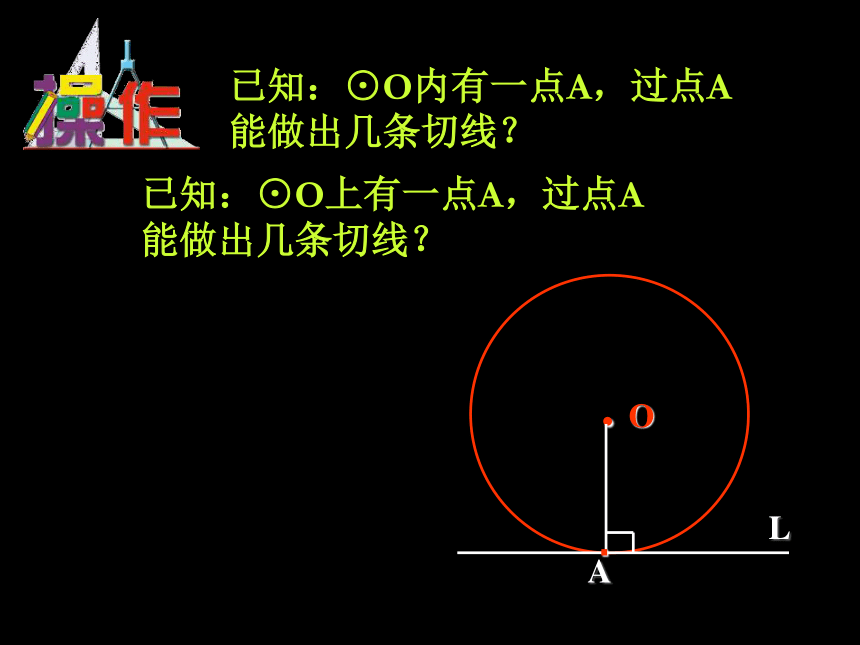
已知:⊙O内有一点A,过点A能做出几条切线?
已知:⊙O上有一点A,过点A能做出几条切线?
.
.
O
A
L
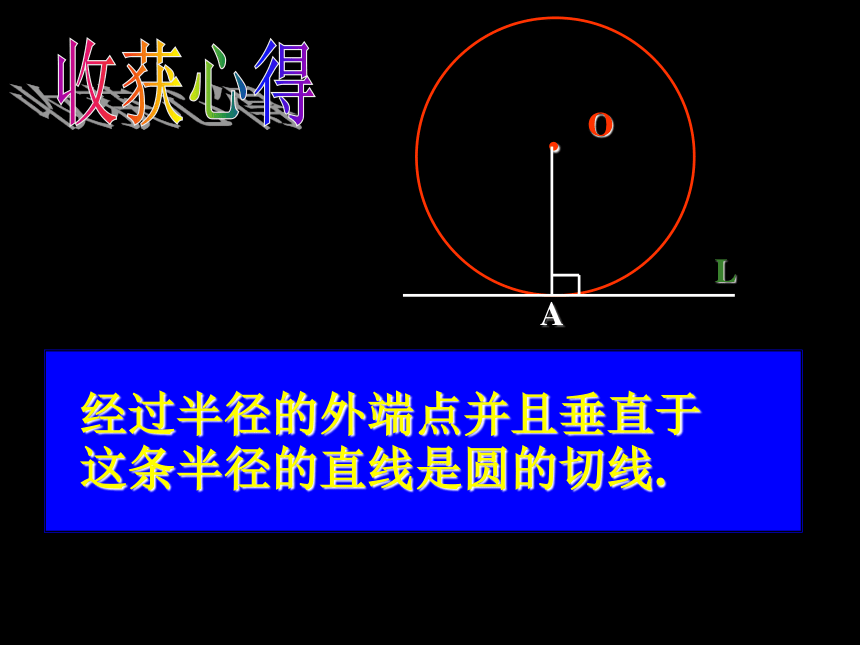
经过半径的外端点并且垂直于这条半径的直线是圆的切线.
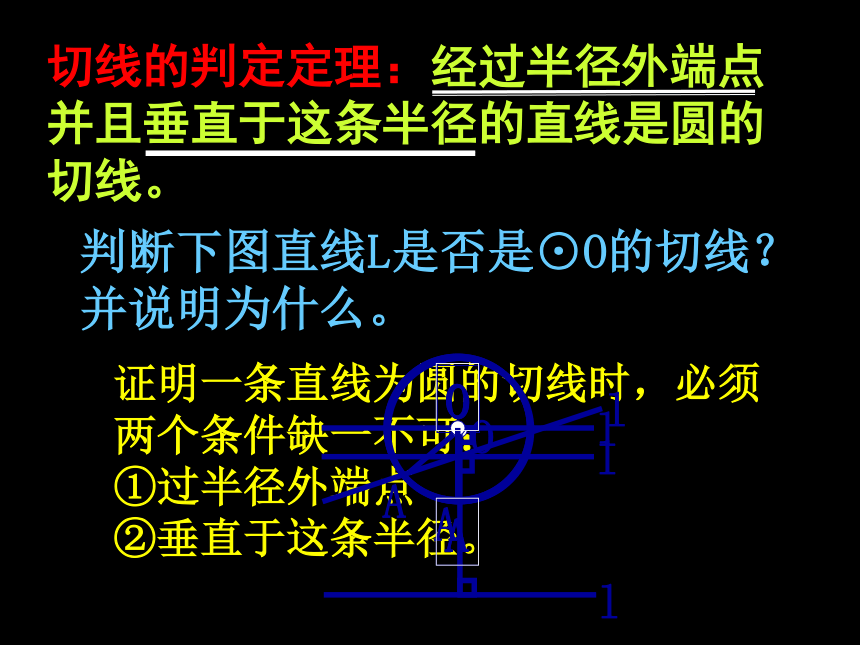
切线的判定定理:经过半径外端点并且垂直于这
条半径的直线是圆的切线.
∟
T
B
A
O
∵直线AB 经过⊙O上的T点
OT⊥AB
∴直线AB是⊙O的切线
这个命题的题设与结论分别是什么?
③是切线(过切点)
②垂直于直线(切线)
①(OT)过圆心
OT是半径
OT⊥AB
∴直线AB是切线
证明一条直线为圆的切线时,必须两个条件缺一不可:
①过半径外端点
②垂直于这条半径。
切线的判定定理:经过半径外端点
并且垂直于这条半径的直线是圆的切线。
l
A
O
O
l
A
O
l
A
O
l
A
O
判断下图直线L是否是⊙O的切线?
并说明为什么。
1.直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
①过半径外端
②垂直于这条半径。
辅助线:
有切点连圆心,证垂直
1.已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC, ∠A=30.
求证:直线AB是⊙O的切线.
B
C
A
练习:
O
2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系,
并证明你的结论。
辅助线:
无切点做垂线,证相等
F
.
O
A
L
已知直线L 是⊙O的切线,切点为A,连接0A,你发现了什么?
切线的性质定理:圆的切线垂直于过切点的半径。
.
O
A
L
切线性质
如图,直线CD与⊙O相切于点A,
直径AB与切线CD有怎样的位置关系
直径AB垂直于切线CD.
C
D
B
●O
A
定理:圆的切线垂直于过切点的半径.
①过半径的外端点
②垂直于这条半径
切线
①圆的切线
②过切点的半径。
切线垂直于半径
判定定理:
性质定理:
1如图, PB切⊙O于点B,PB=4,PA=2,则⊙O的半径多少?
2 如图:PA,PC分别切⊙ O于点A,C两点,B为⊙ O上与A,C不重合的点,若∠P=50°,则∠ABC=___
r=3
65°或 115°
如图(a)AB为⊙O的直径,△ABC
内接于⊙O,且∠CAE=∠B
1、试说明AE与⊙O相切于点A。
2、如图(b),若AB是⊙O的非直径的弦,且∠CAE=∠B,AE与⊙O还相切于点A吗?
F
切线的判定方法
有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.
切线的性质:
定理:圆的切线垂直于过切点的半径.
1、有点连圆心,证垂直
2、无点做垂线,证相等
证明切线时常用辅助线:
25.5 直线和圆的位置关系(2)
-----切线的判定定理和性质定理
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
直线和圆相切
d r;
d r;
直线和圆相交
直线和圆相离
d r;
直线与圆的位置关系
<
=
>
目前,我们学过几种方法可以判定直线与圆相切?
1.看直线与圆交点的个数(有且只有一个)。
2.比较圆心到直线的距离与半径的大小。(d=r)
.
O
A
L
已知:⊙O内有一点A,过点A能做出几条切线?
已知:⊙O上有一点A,过点A能做出几条切线?
.
.
O
A
L
经过半径的外端点并且垂直于这条半径的直线是圆的切线.
切线的判定定理:经过半径外端点并且垂直于这
条半径的直线是圆的切线.
∟
T
B
A
O
∵直线AB 经过⊙O上的T点
OT⊥AB
∴直线AB是⊙O的切线
这个命题的题设与结论分别是什么?
③是切线(过切点)
②垂直于直线(切线)
①(OT)过圆心
OT是半径
OT⊥AB
∴直线AB是切线
证明一条直线为圆的切线时,必须两个条件缺一不可:
①过半径外端点
②垂直于这条半径。
切线的判定定理:经过半径外端点
并且垂直于这条半径的直线是圆的切线。
l
A
O
O
l
A
O
l
A
O
l
A
O
判断下图直线L是否是⊙O的切线?
并说明为什么。
1.直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
①过半径外端
②垂直于这条半径。
辅助线:
有切点连圆心,证垂直
1.已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC, ∠A=30.
求证:直线AB是⊙O的切线.
B
C
A
练习:
O
2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系,
并证明你的结论。
辅助线:
无切点做垂线,证相等
F
.
O
A
L
已知直线L 是⊙O的切线,切点为A,连接0A,你发现了什么?
切线的性质定理:圆的切线垂直于过切点的半径。
.
O
A
L
切线性质
如图,直线CD与⊙O相切于点A,
直径AB与切线CD有怎样的位置关系
直径AB垂直于切线CD.
C
D
B
●O
A
定理:圆的切线垂直于过切点的半径.
①过半径的外端点
②垂直于这条半径
切线
①圆的切线
②过切点的半径。
切线垂直于半径
判定定理:
性质定理:
1如图, PB切⊙O于点B,PB=4,PA=2,则⊙O的半径多少?
2 如图:PA,PC分别切⊙ O于点A,C两点,B为⊙ O上与A,C不重合的点,若∠P=50°,则∠ABC=___
r=3
65°或 115°
如图(a)AB为⊙O的直径,△ABC
内接于⊙O,且∠CAE=∠B
1、试说明AE与⊙O相切于点A。
2、如图(b),若AB是⊙O的非直径的弦,且∠CAE=∠B,AE与⊙O还相切于点A吗?
F
切线的判定方法
有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.
切线的性质:
定理:圆的切线垂直于过切点的半径.
1、有点连圆心,证垂直
2、无点做垂线,证相等
证明切线时常用辅助线:
