2-3变量间的相关关系(2)

(共12张PPT)
2、回归直线方程
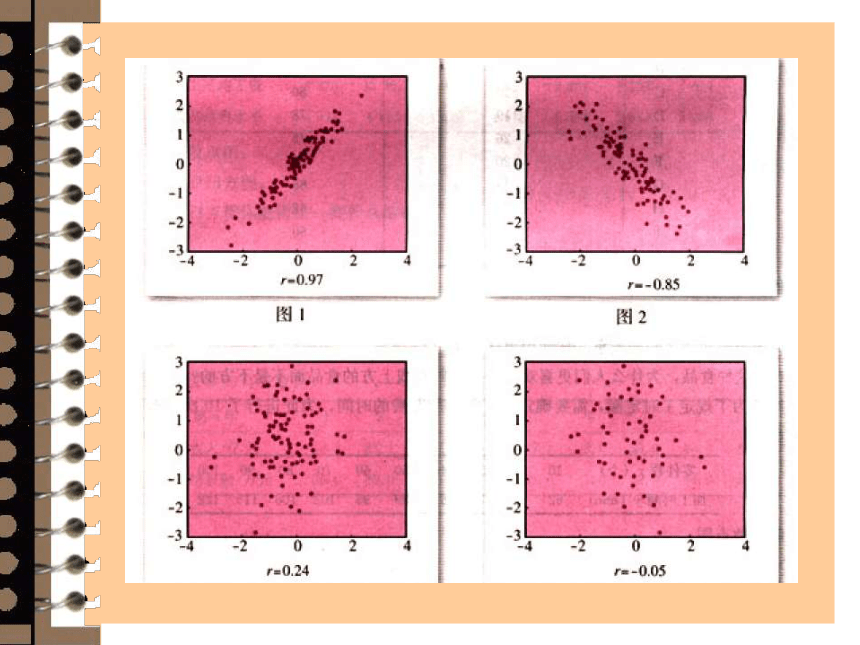
（1）回归直线：观察散点图的特征，如果各点大致分布在一条直线的附近，就称两个变量之间具有线性相关的关系，这条直线叫做回归直线。
（2）最小二乘法
A、定义；B、正相关、负相关。
一、复习: 1、散点图
一、相关关系的判断
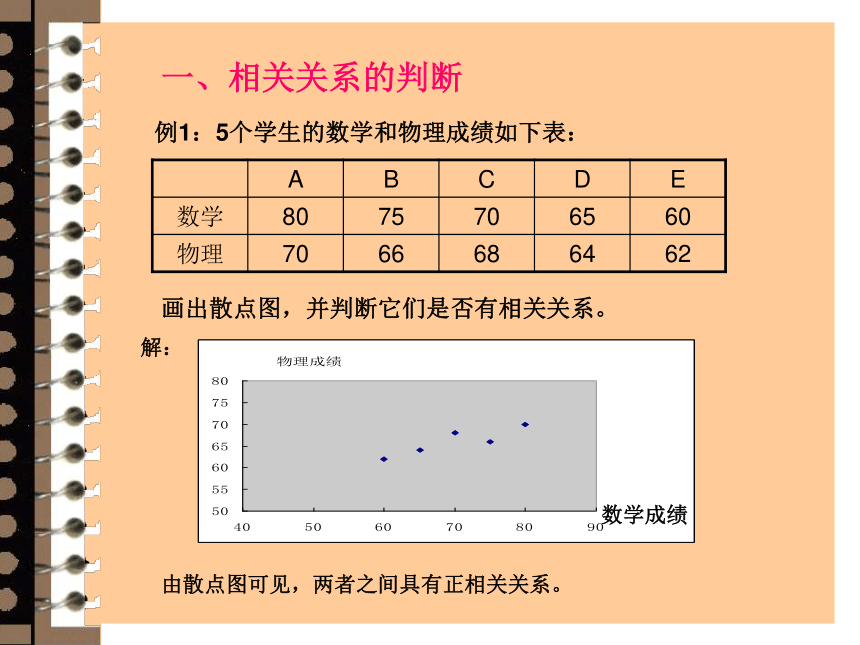
例1：5个学生的数学和物理成绩如下表：
A B C D E
数学 80 75 70 65 60
物理 70 66 68 64 62
画出散点图，并判断它们是否有相关关系。
解：
数学成绩
由散点图可见，两者之间具有正相关关系。
小结：用Excel作散点图的步骤如下 ： (结合软件边讲边练）
（1）进入Excel，在A1，B1分别输入“数学成绩”、“物理成绩”，在A、B列输入相应的数据。
（2）点击图表向导图标，进入对话框，选择“标准类型”中的“XY散点图”，单击“完成”。
（3）选中“数值X轴”，单击右键选中“坐标轴格式”中的“刻度”，把“最小值”、“最大值”、“刻度主要单位”作相应调整，最后按“确定”。y轴方法相同。
二、求线性回归方程
例2：观察两相关变量得如下表：
x -1 -2 -3 -4 -5 5 3 4 2 1
y -9 -7 -5 -3 -1 1 5 3 7 9
求两变量间的回归方程
解1：
列表：
i 1 2 3 4 5 6 7 8 9 10
-1 -2 -3 -4 -5 5 3 4 2 1
-9 -7 -5 -3 -1 1 5 3 7 9
9 14 15 12 5 5 15 12 14 9
计算得:
∴所求回归直线方程为 y=x
^
小结：求线性回归直线方程的步骤：
第一步：列表 ；
第二步：计算 ；
第三步：代入公式计算b,a的值；
第四步：写出直线方程。
解2：用Excel求线性回归方程，步骤如下:
.
（1）进入Excel作出散点图。
（2）点击“图表”中的“添加趋势线”，单击“类型”中的“线性”，单击“确定”，得到回归方程。
（3）双击回归直线，弹出“趋势线格式”，单击“选项”，选定“显示公式”，最后单击“确定”。
例：有一个同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计，得到一个卖出的热饮杯数与当天气温的对比表：
摄氏温度 -5 0 4 7 12 15 19 23 27 31 36
热饮杯数 156 150 132 128 130 116 104 89 93 76 54
(1)画出散点图；
(2)从散点图中发现气温与热饮销售杯数之间关系的一
般规律；
(3)求回归方程；
(4)如果某天的气温是 C,预测这天卖出的热饮杯数。
三、利用线性回归方程对总体进行估计
解: (1)散点图
(2)气温与热饮杯数成负相关,即气温越高， 卖出去的热饮杯数越少。
温度
热饮杯数
(3)从散点图可以看出，这些点大致分布在一条直线附近。
Y=-2.352x+147.767
^
（4）当x=2时，y=143.063,因此，这天大约可以卖出143杯热饮。
^
练习：P86第三题
小结：
（1）判断变量之间有无相关关系，简便方法就是画散点图。
（2）当数字少时，可用人工或计算器，求回归方程；当数字多时，用Excel求回归方程。
（3）利用回归方程，可以进行预测。