同底数幂的乘法
图片预览







文档简介
(共21张PPT)
问题: 光的速度约为3×105千米/秒,太阳光照射到地球大约需要5×102秒.地球距离太阳大约有多远?
解: 3×105×5×102
=15×105×102 (千米)
等于多少呢?
105×102
太阳离我们有多远?
15.1.1 同底数幂的乘法
周老嘴直荀中学 刘梦碧
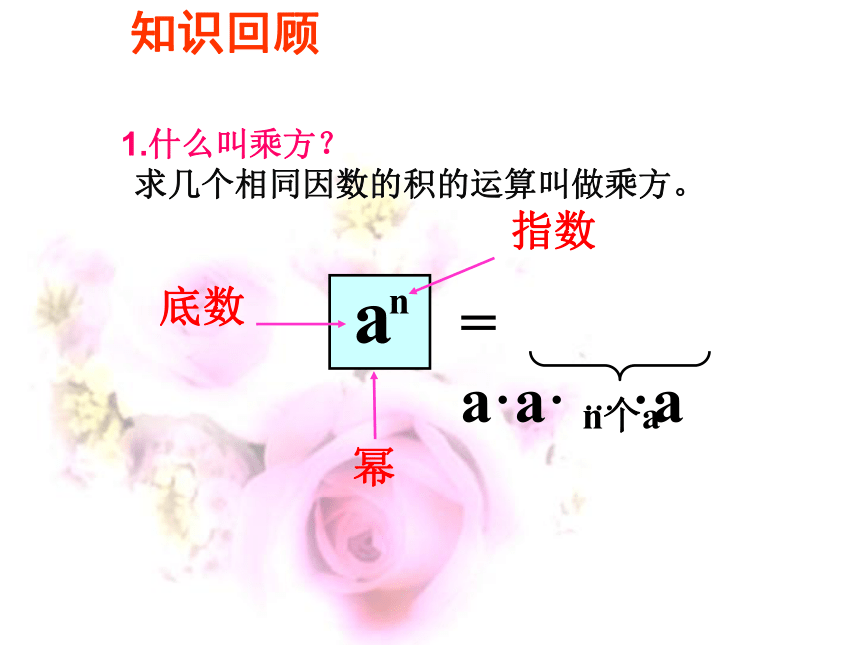
a
n
指数
幂
= a·a· … ·a
n个a
底数
1.什么叫乘方?
求几个相同因数的积的运算叫做乘方。
知识回顾
25表示什么?
10×10×10×10×10 可以写成什么形式
问题:
25 = .
2×2×2×2×2
105
10×10×10×10×10 = .
(乘方的意义)
(乘方的意义)
式子103×102的意义是什么?
思考:
103与102 的积
底数相同 ,指数不同,即同底数幂
这个式子中的两个因数有何特点?
请同学们先根据自己的理解,解答下列各题。
103 ×102 =
(10×10×10)×(10×10)
=10×10×10×10×10
=105
(乘方的意义)
(乘法结合律)
(乘方的意义)
思考:
底数相同
请同学们先根据自己的理解,大胆猜想其结果,再细细想想你的结果有什么依据?
103 ×102 = = 10( );
23 ×22 =
= 2( );
(10×10×10)
5
×(10×10)
5
(2×2×2)×(2×2)
=2×2×2×2×2
a3×a2 = = a( ) 。
(a a a)
5
.(a a)
= a a a a a
3个a
2个a
5个a
思考:
请同学们观察下面各题左右两边,底数、指数有什么关系?
103 ×102 = 10( )
23 ×22 = 2( )
a3× a2 = a( )
5
5
5
猜想: am · an= (当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确。
3+2
3+2
3+2
= 10( );
= 2( );
= a( ) 。
猜想: am · an= (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a).
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
真不错,你的猜想是正确的!
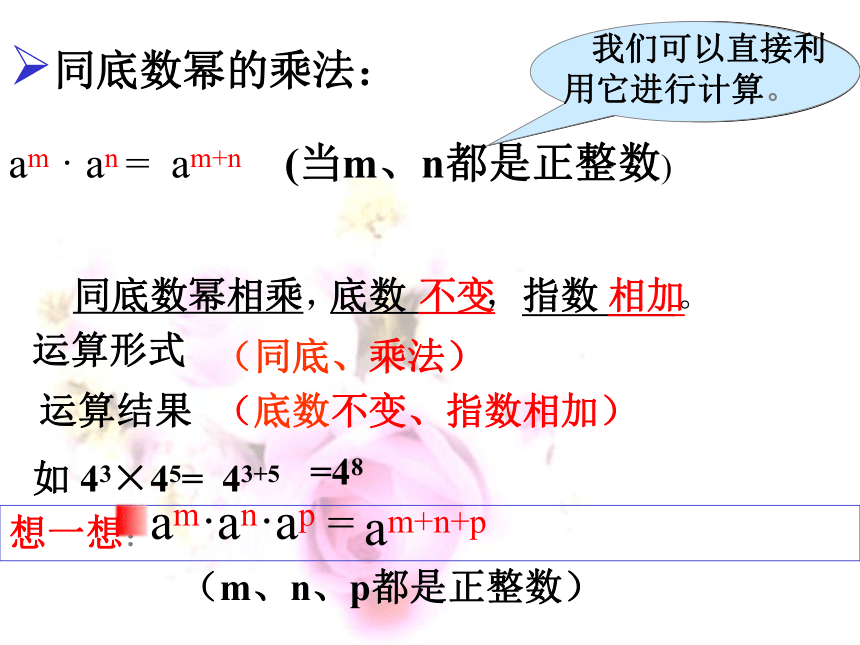
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
想一想:
底数 ,指数 。
不变
相加
同底数幂的乘法:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算。
如 43×45=
43+5
=48
am·an·ap =
am+n+p
(m、n、p都是正整数)
运算形式
运算结果
(同底、乘法)
(底数不变、指数相加)
开头问题中地球距离太阳到底大约有多远呢?
15×105×102
=15×107
=1.5×108(千米)
地球距离太阳大约有1.5×108千米.
飞行这么远的距离,一架喷气式客机大约要20年呢!
=1.5×10×107
例1.计算:
(1)108 ×103 ; (2)x3 · x5 .
解:(1)108 ×103 =108 +3= 1011
(2)x3 · x5 = x3 + 5 = x8
例2.计算:(1)23×24×25 (2)y · y3 · y5
解:(1)23×24×25=23+4+5=212
(2)y · y3 · y5 = y1+3+5=y9
am · an = am+n (当m、n都是正整数) am·an·ap = am+n+p (m、n、p都是正整数)
y的指数是1
指数较大时,结果以幂的形式表示.
练习一
1. 计算:(抢答)
( 710 )
( a15 )
( x8 )
( b6 )
(2) a7 ·a8
(3) x5 ·x3
(4) b5 · b
(1) 76×74
Good!
练习二
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x2 = x10 ( ) (4)y5 +2 y5 =3y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x2 = x7
y5 + 2 y5 =3y5
c · c3 = c4
×
×
×
×
×
×
了不起!
思考题
(1) x n · xn+1
(2) (x+y)3 · (x+y)4
1.计算:
解:
x n · xn+1 =
解:
(x+y)3 · (x+y)4 =
am · an = am+n
xn+(n+1)
= x2n+1
公式中的a可代表一个数、字母、式子等。
(x+y)3+4 =(x+y)7
(-2)3×(-2)5
(2) (-2)2×(-2)7
(3) (-2)3×25
(4) (-2)2×27
( 28 )
(-29 )
(- 28 )
( 29 )
化同底数一
化异为同
化同底数二
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = 。
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
化繁为简
小结
这节课你学到了什么
你有什么收获
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
小 结
我学到了什么?
知识
方法
“特殊→一般→特殊”
例子 公式 应用
不变,
相加.
1.计算
(1)a3.(-a)4 (2)m5.(-m4)
(3)(-x)3.(-x)2.(-x)5
(4)(x-y)2.(y-x)
2.若m=-2求-m.(-m)4.(-m)3的值
3.课本P142 计算
练 习
趣味创新
计算:
2-22-23-24-25-26-27-28-29+210.
原式=210-29-28-27-26-25-24-23-22+2
=2·29-29-28-27-26-25-24-23-22+2
=29-28-27-26-25-24-23-22+2
=…
=22+2=6 .
问题: 光的速度约为3×105千米/秒,太阳光照射到地球大约需要5×102秒.地球距离太阳大约有多远?
解: 3×105×5×102
=15×105×102 (千米)
等于多少呢?
105×102
太阳离我们有多远?
15.1.1 同底数幂的乘法
周老嘴直荀中学 刘梦碧
a
n
指数
幂
= a·a· … ·a
n个a
底数
1.什么叫乘方?
求几个相同因数的积的运算叫做乘方。
知识回顾
25表示什么?
10×10×10×10×10 可以写成什么形式
问题:
25 = .
2×2×2×2×2
105
10×10×10×10×10 = .
(乘方的意义)
(乘方的意义)
式子103×102的意义是什么?
思考:
103与102 的积
底数相同 ,指数不同,即同底数幂
这个式子中的两个因数有何特点?
请同学们先根据自己的理解,解答下列各题。
103 ×102 =
(10×10×10)×(10×10)
=10×10×10×10×10
=105
(乘方的意义)
(乘法结合律)
(乘方的意义)
思考:
底数相同
请同学们先根据自己的理解,大胆猜想其结果,再细细想想你的结果有什么依据?
103 ×102 = = 10( );
23 ×22 =
= 2( );
(10×10×10)
5
×(10×10)
5
(2×2×2)×(2×2)
=2×2×2×2×2
a3×a2 = = a( ) 。
(a a a)
5
.(a a)
= a a a a a
3个a
2个a
5个a
思考:
请同学们观察下面各题左右两边,底数、指数有什么关系?
103 ×102 = 10( )
23 ×22 = 2( )
a3× a2 = a( )
5
5
5
猜想: am · an= (当m、n都是正整数)
分组讨论,并尝试证明你的猜想是否正确。
3+2
3+2
3+2
= 10( );
= 2( );
= a( ) 。
猜想: am · an= (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a).
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
真不错,你的猜想是正确的!
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
想一想:
底数 ,指数 。
不变
相加
同底数幂的乘法:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算。
如 43×45=
43+5
=48
am·an·ap =
am+n+p
(m、n、p都是正整数)
运算形式
运算结果
(同底、乘法)
(底数不变、指数相加)
开头问题中地球距离太阳到底大约有多远呢?
15×105×102
=15×107
=1.5×108(千米)
地球距离太阳大约有1.5×108千米.
飞行这么远的距离,一架喷气式客机大约要20年呢!
=1.5×10×107
例1.计算:
(1)108 ×103 ; (2)x3 · x5 .
解:(1)108 ×103 =108 +3= 1011
(2)x3 · x5 = x3 + 5 = x8
例2.计算:(1)23×24×25 (2)y · y3 · y5
解:(1)23×24×25=23+4+5=212
(2)y · y3 · y5 = y1+3+5=y9
am · an = am+n (当m、n都是正整数) am·an·ap = am+n+p (m、n、p都是正整数)
y的指数是1
指数较大时,结果以幂的形式表示.
练习一
1. 计算:(抢答)
( 710 )
( a15 )
( x8 )
( b6 )
(2) a7 ·a8
(3) x5 ·x3
(4) b5 · b
(1) 76×74
Good!
练习二
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x2 = x10 ( ) (4)y5 +2 y5 =3y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x2 = x7
y5 + 2 y5 =3y5
c · c3 = c4
×
×
×
×
×
×
了不起!
思考题
(1) x n · xn+1
(2) (x+y)3 · (x+y)4
1.计算:
解:
x n · xn+1 =
解:
(x+y)3 · (x+y)4 =
am · an = am+n
xn+(n+1)
= x2n+1
公式中的a可代表一个数、字母、式子等。
(x+y)3+4 =(x+y)7
(-2)3×(-2)5
(2) (-2)2×(-2)7
(3) (-2)3×25
(4) (-2)2×27
( 28 )
(-29 )
(- 28 )
( 29 )
化同底数一
化异为同
化同底数二
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = 。
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
化繁为简
小结
这节课你学到了什么
你有什么收获
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
小 结
我学到了什么?
知识
方法
“特殊→一般→特殊”
例子 公式 应用
不变,
相加.
1.计算
(1)a3.(-a)4 (2)m5.(-m4)
(3)(-x)3.(-x)2.(-x)5
(4)(x-y)2.(y-x)
2.若m=-2求-m.(-m)4.(-m)3的值
3.课本P142 计算
练 习
趣味创新
计算:
2-22-23-24-25-26-27-28-29+210.
原式=210-29-28-27-26-25-24-23-22+2
=2·29-29-28-27-26-25-24-23-22+2
=29-28-27-26-25-24-23-22+2
=…
=22+2=6 .
