指数函数图象及性质

(共15张PPT)
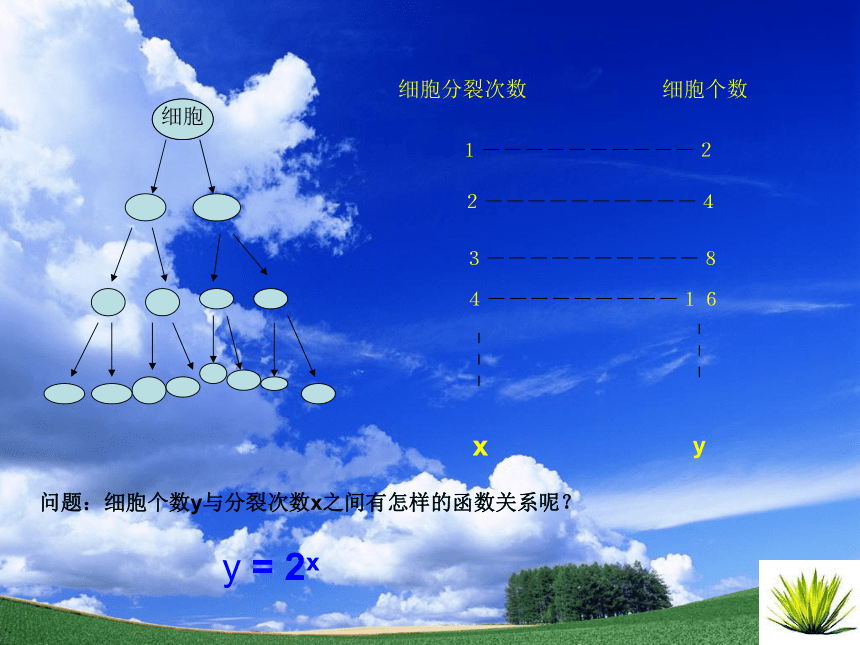
细胞分裂次数
细胞个数
１－－－－－－－－－－２
２－－－－－－－－－－４
３－－－－－－－－－－８
４－－－－－－－－－１６
－－－
x
－－－
y
细胞
问题：细胞个数y与分裂次数x之间有怎样的函数关系呢？
y = 2x
定义：一般地，函数y＝ax（a>0，且a≠1）叫做指数函数，其中x是自变量，a称为指数函数的底，函数的定义域是R。
巩固练习：判断下列哪些函数是
指数函数
⑴ y=4x ⑵ y=4x
⑶ y=x4 ⑷ y= -2x
答：只有⑵是指数函数
定义：一般地，函数y＝ax（a>0，且a≠1）叫做指数函数，其中x是自变量，
a称为指数函数的底，函数的定义域是R。
例1：在同一个直角坐标系中，
(1) 作出指数函数 y = 2x 与 y = 3x 图象
(2) 作出指数函数 y =(1/2)x 与 y = (1/3)x　图象
定义：一般地，函数y＝ax（a>0，且a≠1）叫做指数函数，
　　 其中x是自变量，函数的定义域是R
例1：在同一个直角坐标系中，
(1) 作出指数函数 y = 2x 与 y = 3x 图象
(2) 作出指数函数 y =(1/2)x 与 y = (1/3)x　图象
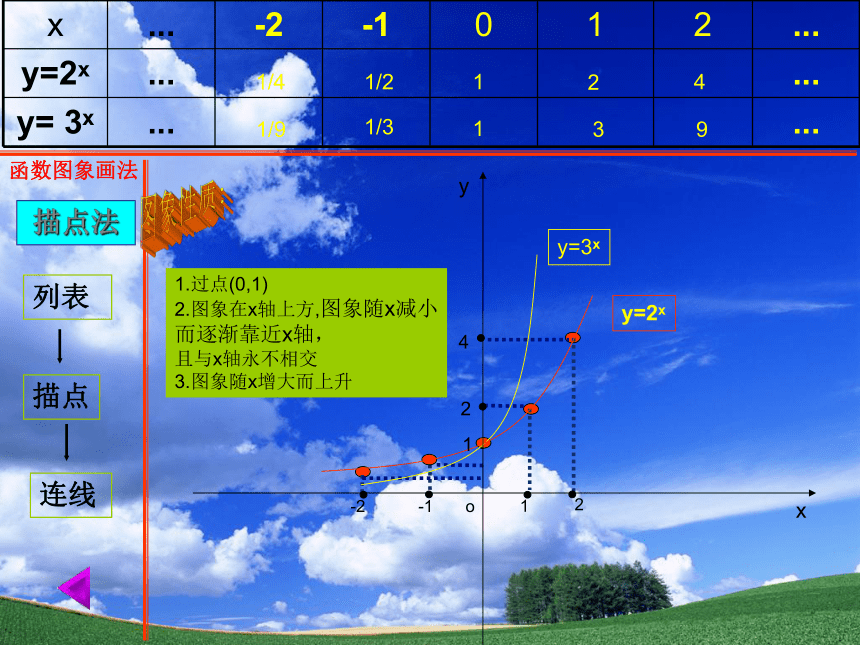
x ... -2 -1 0 1 2 ...
y=2x ... ...
y= 3x ... ...
1/4
1/2
1
2
1/9
1/3
1
3
9
4
函数图象画法
描点法
列表
描点
连线
1.过点(0,1)
2.图象在x轴上方,图象随x减小
而逐渐靠近x轴，
且与x轴永不相交
3.图象随x增大而上升
4
y=3x
y=2x
x
o
-2
-1
1
2
1
2
y
1
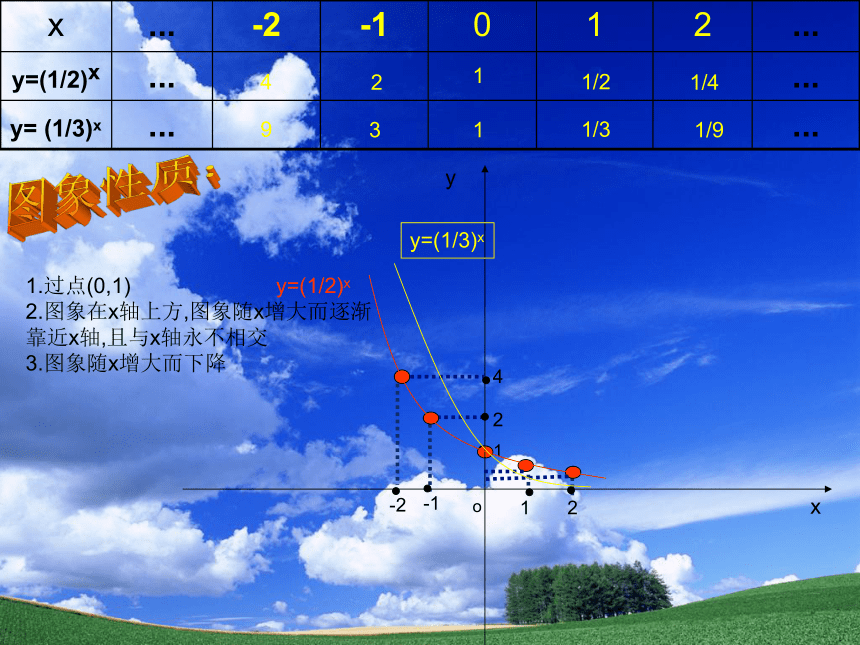
x ... -2 -1 0 1 2 ...
y=(1/2)x ... ...
y= (1/3)x ... ...
1
1/2
1/4
2
4
9
3
1
1/3
1/9
x
y
o
-2
-1
1
2
2
4
y=(1/2)x
y=(1/3)x
1.过点(0,1)
2.图象在x轴上方,图象随x增大而逐渐
靠近x轴,且与x轴永不相交
3.图象随x增大而下降
y=3x
y=2x
x
y
o
-2
-1
1
2
2
x
y
o
y=(1/3)x
y=(1/2)x
1.过点(0,1)
2.图象在x轴上方,且与x轴不相交
图象随x减小而逐渐靠近x轴
3.图象随x增大而上升
1.过点(0,1)
2.图象在x轴上方,且与x轴不相交
图象随x增大而逐渐靠近x轴
3.图象随x增大而下降
1
1
a >1
1. 经 过 ( 0 , 1 ) 点
x
y
1
o
5.在R上是增函数
3.图象随x无限减小而逐渐靠近x轴
图 象
性 质
0< a <1
x
y
1
o
4.图象在x轴上方,
2. 定义域:R,值域（0，+∞）
2. 定义域:R，值域（0，+∞）
1. 经 过 ( 0 , 1 ) 点
3.图象随x无限增大而逐渐靠近x轴
4.图象在x轴上方
5.在R上是减函数
思考：在同一个坐标系中，y=2x与y=(1/2)x图象的关系
x ... -2 -1 0 1 2 ...
y=2x ... 1/4 1/2 １ ２ 4 ...
y=(1/2)x ... 4 ２ １ 1/2 1/4 ...
x
y
1
o
y=(1/2)x
y=2x
结论1：y=ax与y=(1/a)x的图象关于y轴对称
y=2x与y=(1/2)x图象关于y轴对称
y=3x
y=(1/3)x
y=3x与y=(1/3)x图象关于y轴对称
结论2:在第一象限,底数越大图象越靠近y轴
思考：在同一个坐标系中，y=2x与y=(1/2)x图象的关系
x ... -2 -1 0 1 2 ...
y=2x ... 1/4 1/2 １ ２ 4 ...
y=(1/2)x ... 4 ２ １ 1/2 1/4 ...
x
y
1
o
y=(1/2)x
y=2x
结论1：y=ax与y=(1/a)x的图象关于y轴对称
y=2x与y=(1/2)x图象关于y轴对称
y=3x
y=(1/3)x
y=3x与y=(1/3)x图象关于y轴对称
结论2:在第一象限,底数越大图象越靠近y轴
例题2:根据下列指数函数图象,判断a , b ,c , d的大小
x
y
1
o
y=dx
y=cx
y=bx
y=ax
分析:⑴在第一象限,底数越大图象越靠近y轴
c > d > a > b
c > 1，d >1
0< a<1, 0< b<1
⑵根据指数函数定义性质,
综上:c>d>1>a>b>0
a >1
1. 经 过 ( 0 , 1 ) 点
x
y
1
o
5.在R上是增函数
3.图象随x无限减小而逐渐靠近x轴
图 象
性 质
0< a <1
x
y
1
o
4.图象在x轴上方,值域:{ y ∣y >0 }
2. 定义域:R
2. 定义域:R
1. 经 过 ( 0 , 1 ) 点
3.图象随x无限增大而逐渐靠近x轴
4.图象在x轴上方,值域:{ y ∣y >0 }
5.在R上是减函数
板书设计
指数函数
1.定义：--------
2.性质：
a >1 0< a <1
图象
性质
例1：⑴------------------- ⑵-----------------------
列表—描点---连线
图象：--------
图象：--------
性质：--------
性质：--------
作业：--------