新人教版数学七年级上 3.3一元一次方程应用(工作量问题)
文档属性
| 名称 | 新人教版数学七年级上 3.3一元一次方程应用(工作量问题) |  | |
| 格式 | zip | ||
| 文件大小 | 574.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-10 21:56:08 | ||
图片预览







文档简介
(共20张PPT)
3.3 解一元一次方程
(第4课时 )
你能选用适当的方法解下列方程吗
请动手试试看.
3
1-2x
6
10x+1
4
2x+1
(4)
+
=1-
动手做一做
(1)2ⅹ+ⅹ=25+5
(2)8ⅹ- 2=7ⅹ- 2
(3)2(ⅹ+3)- 3(ⅹ-1)=5(1-ⅹ)
1.进一步熟悉含有分母的一元一次方程的解法。
2.能够列一元一次方程解决生活中的工程问题。
学 习 目 标
1、解一元一次方程时一般有哪几个 步骤
一起说一说
2、各个步骤的依据分别是什么
3、做每一步时应该要注意什么
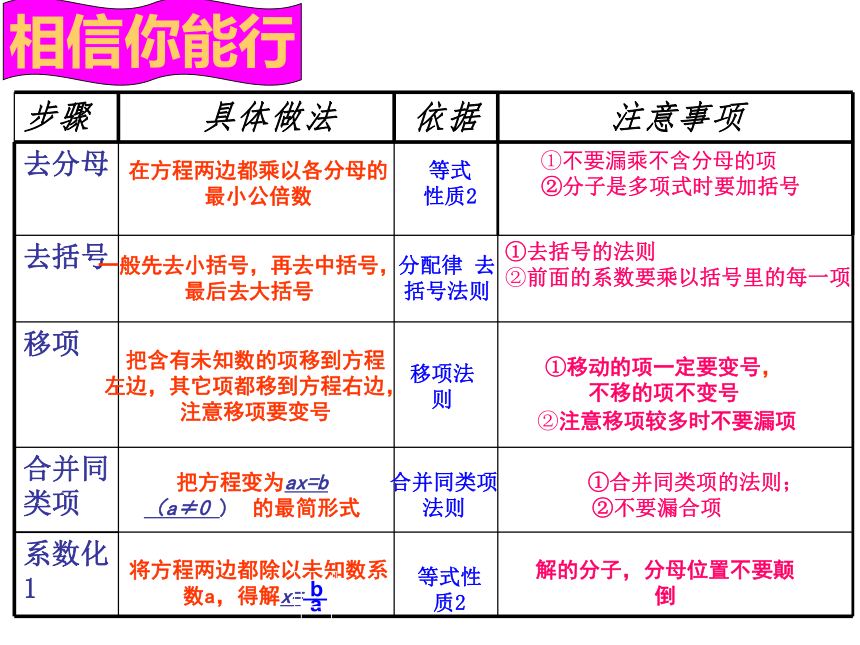
步骤 具体做法 依据 注意事项
去分母
去括号
移项
合并同类项
系数化1
在方程两边都乘以各分母的最小公倍数
等式
性质2
①不要漏乘不含分母的项
②分子是多项式时要加括号
一般先去小括号,再去中括号,最后去大括号
分配律 去括号法则
把含有未知数的项移到方程
左边,其它项都移到方程右边,注意移项要变号
移项法则
①移动的项一定要变号,
不移的项不变号
②注意移项较多时不要漏项
把方程变为ax=b
(a≠0 ) 的最简形式
合并同类项法则
①合并同类项的法则;
②不要漏合项
将方程两边都除以未知数系
数a,得解x=
等式性质2
解的分子,分母位置不要颠倒
相信你能行
①去括号的法则
②前面的系数要乘以括号里的每一项
a
__
b
0.3
x
=1 +
0.2
1.2-0.3x
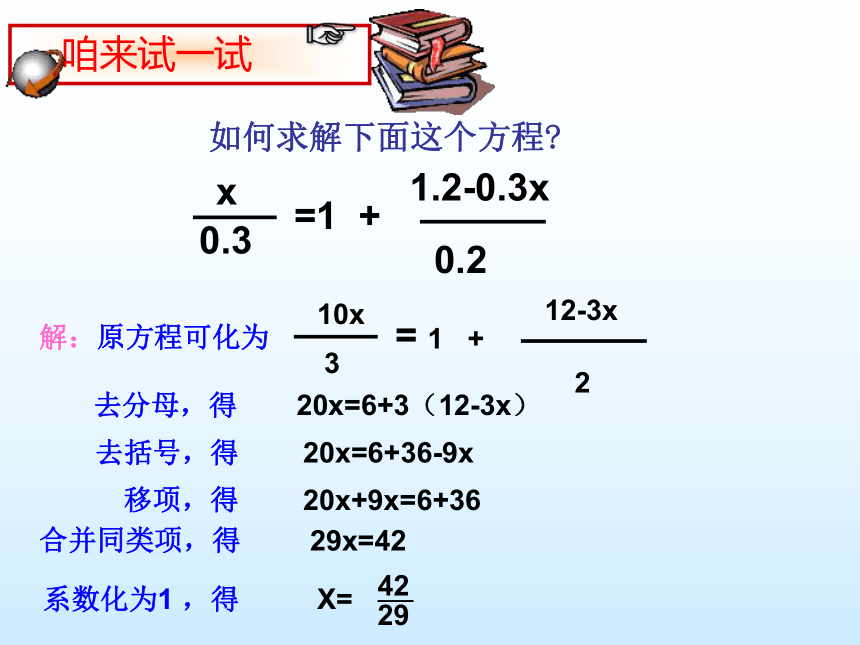
如何求解下面这个方程
咱来试一试
解:原方程可化为
3
10x
= 1 +
2
12-3x
去分母,得
20x=6+3(12-3x)
去括号,得
20x=6+36-9x
移项,得
20x+9x=6+36
合并同类项,得
29x=42
系数化为1 ,得
X=
42
___
29
练一练:
咱来试一试
解方程:
0.7
x
–
0.03
0.17-0.2x
=1
你还记得吗
1、一项工程,甲独做需6天,乙独做需12天,
把总工作量看作1,两人合做一天的工作量是
,两人合做 天完成。
工程问题
工作效率×工作时间=工作总量
________
2、一项工作,12个人4个小时才能完成。若这项工作由8个人来做,要 小时才能完成。
——————
4
__
1
4
6
整理一批图书,由一个人做要40小时完成。现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作。假设这些人的工作效率相同,具体应先安排多少人工作
思考:
每一个人的工作效率是多少 完成这项工作(整理图书)分为几个过程 问题中的等量关系是什么
问题探究
分析:这里可以把工作总量看作
1
请填空:
人均效率(一个人做1小时完成的工作量)为
由x人先做4小时,完成的工作量为
再增加2人和前一部分人一起做8小时,完成任务的
工作量为
这项工作分两段完成任务,两段完成任务的工作量
之和为
或 1
___
1
40
4x
___
40
8(x+2)
______
40
40
___
4x
______
40
8(x+2)
+
例5
解:
设先安排了x人工作4小时。根据题意,得
去分母,得
去括号,得
移项,得
合并,得
系数化为1,得
答:应先安排2名工人工作4小时。
例 题 详 解
(1)工程问题中的基本量及其关系:
(2)若问题中工作量未知,通常可把
总工作量看作
(3)利用 是工程问题
中常用的等量关系
工作量=人均效率 × 人数 ×时间
各阶段工作量的和=总工作量
各人完成的工作量的和=完成的工作总量
归 纳
工作量=工作效率×工作时间
1
部分工作量之和等于总量
即:
巩 固 练 习
整理一批图书,如果一个人单独做要花60小时。现先由一部分人用1小时整理,随后增加15人和他们一起又做了两小时恰好完成整理工作。假设这些人的工作效率相同,求一开始安排的人数。
各阶段的工作量之和=总工作量1
变 式 练 习
整理一批图书,如果一个人单独做要花60小时。现先由一部分人用1小时整理后,有5人因故离开,剩下的人又做了4小时完成了这项工作。假设这些人的工作效率相同,求一开始安排的人数。
有一道题只写了“学校校办厂需制作一块广告牌,请来2名工人.已知师傅完成需3天,徒弟单独完成需要6天.”
请你补充一个问题并解答
你能想出几种问题方案呢 请你大胆地试一试.
大胆来尝试
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
感悟与反思
布置作业
1、课本102页 8题、9题
2、预习课本104页,同 步学习88页内容。
祝同学们学习进步! 再见
巩 固 练 习
一项工作,甲单独做要20小时完成,乙单独做要12小时完成。现在先由甲单独做4小时,剩下的部分由甲、乙合作。剩下的部分需要多少小时完成?
甲独做的工做量+甲乙合作的工作量=1
一个水池有甲.乙.丙三个水管,甲.乙是入水管,丙是排水管,单开甲管16 分钟可将水池注满,单开乙管10分钟可将水池注满,单开丙管20分钟可将满池水放完.现在先开甲乙两管,4分钟后关上甲管开丙管,问又经过几分钟才能将水池注满
讨论与探究
为庆祝校运会开幕,我班学生接受了制作校旗的任务.原计划一半同学参加制作,每天制作40面.而实际上,在完成了三分之一以后,全班同学一起参加,结果比原计划提前一天半完成任务.假设每人的制作效率相同,问共制作校旗多少面
讨论与探究
3.3 解一元一次方程
(第4课时 )
你能选用适当的方法解下列方程吗
请动手试试看.
3
1-2x
6
10x+1
4
2x+1
(4)
+
=1-
动手做一做
(1)2ⅹ+ⅹ=25+5
(2)8ⅹ- 2=7ⅹ- 2
(3)2(ⅹ+3)- 3(ⅹ-1)=5(1-ⅹ)
1.进一步熟悉含有分母的一元一次方程的解法。
2.能够列一元一次方程解决生活中的工程问题。
学 习 目 标
1、解一元一次方程时一般有哪几个 步骤
一起说一说
2、各个步骤的依据分别是什么
3、做每一步时应该要注意什么
步骤 具体做法 依据 注意事项
去分母
去括号
移项
合并同类项
系数化1
在方程两边都乘以各分母的最小公倍数
等式
性质2
①不要漏乘不含分母的项
②分子是多项式时要加括号
一般先去小括号,再去中括号,最后去大括号
分配律 去括号法则
把含有未知数的项移到方程
左边,其它项都移到方程右边,注意移项要变号
移项法则
①移动的项一定要变号,
不移的项不变号
②注意移项较多时不要漏项
把方程变为ax=b
(a≠0 ) 的最简形式
合并同类项法则
①合并同类项的法则;
②不要漏合项
将方程两边都除以未知数系
数a,得解x=
等式性质2
解的分子,分母位置不要颠倒
相信你能行
①去括号的法则
②前面的系数要乘以括号里的每一项
a
__
b
0.3
x
=1 +
0.2
1.2-0.3x
如何求解下面这个方程
咱来试一试
解:原方程可化为
3
10x
= 1 +
2
12-3x
去分母,得
20x=6+3(12-3x)
去括号,得
20x=6+36-9x
移项,得
20x+9x=6+36
合并同类项,得
29x=42
系数化为1 ,得
X=
42
___
29
练一练:
咱来试一试
解方程:
0.7
x
–
0.03
0.17-0.2x
=1
你还记得吗
1、一项工程,甲独做需6天,乙独做需12天,
把总工作量看作1,两人合做一天的工作量是
,两人合做 天完成。
工程问题
工作效率×工作时间=工作总量
________
2、一项工作,12个人4个小时才能完成。若这项工作由8个人来做,要 小时才能完成。
——————
4
__
1
4
6
整理一批图书,由一个人做要40小时完成。现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作。假设这些人的工作效率相同,具体应先安排多少人工作
思考:
每一个人的工作效率是多少 完成这项工作(整理图书)分为几个过程 问题中的等量关系是什么
问题探究
分析:这里可以把工作总量看作
1
请填空:
人均效率(一个人做1小时完成的工作量)为
由x人先做4小时,完成的工作量为
再增加2人和前一部分人一起做8小时,完成任务的
工作量为
这项工作分两段完成任务,两段完成任务的工作量
之和为
或 1
___
1
40
4x
___
40
8(x+2)
______
40
40
___
4x
______
40
8(x+2)
+
例5
解:
设先安排了x人工作4小时。根据题意,得
去分母,得
去括号,得
移项,得
合并,得
系数化为1,得
答:应先安排2名工人工作4小时。
例 题 详 解
(1)工程问题中的基本量及其关系:
(2)若问题中工作量未知,通常可把
总工作量看作
(3)利用 是工程问题
中常用的等量关系
工作量=人均效率 × 人数 ×时间
各阶段工作量的和=总工作量
各人完成的工作量的和=完成的工作总量
归 纳
工作量=工作效率×工作时间
1
部分工作量之和等于总量
即:
巩 固 练 习
整理一批图书,如果一个人单独做要花60小时。现先由一部分人用1小时整理,随后增加15人和他们一起又做了两小时恰好完成整理工作。假设这些人的工作效率相同,求一开始安排的人数。
各阶段的工作量之和=总工作量1
变 式 练 习
整理一批图书,如果一个人单独做要花60小时。现先由一部分人用1小时整理后,有5人因故离开,剩下的人又做了4小时完成了这项工作。假设这些人的工作效率相同,求一开始安排的人数。
有一道题只写了“学校校办厂需制作一块广告牌,请来2名工人.已知师傅完成需3天,徒弟单独完成需要6天.”
请你补充一个问题并解答
你能想出几种问题方案呢 请你大胆地试一试.
大胆来尝试
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
感悟与反思
布置作业
1、课本102页 8题、9题
2、预习课本104页,同 步学习88页内容。
祝同学们学习进步! 再见
巩 固 练 习
一项工作,甲单独做要20小时完成,乙单独做要12小时完成。现在先由甲单独做4小时,剩下的部分由甲、乙合作。剩下的部分需要多少小时完成?
甲独做的工做量+甲乙合作的工作量=1
一个水池有甲.乙.丙三个水管,甲.乙是入水管,丙是排水管,单开甲管16 分钟可将水池注满,单开乙管10分钟可将水池注满,单开丙管20分钟可将满池水放完.现在先开甲乙两管,4分钟后关上甲管开丙管,问又经过几分钟才能将水池注满
讨论与探究
为庆祝校运会开幕,我班学生接受了制作校旗的任务.原计划一半同学参加制作,每天制作40面.而实际上,在完成了三分之一以后,全班同学一起参加,结果比原计划提前一天半完成任务.假设每人的制作效率相同,问共制作校旗多少面
讨论与探究
