3.2 独立性检验的基本思想及其初步应用 课堂小练习(含解析)
文档属性
| 名称 | 3.2 独立性检验的基本思想及其初步应用 课堂小练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 309.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 21:41:04 | ||
图片预览


文档简介
3.2 独立性检验的基本思想及其初步应用
1.下列说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;②设有一个线性回归方程,变量x增加1个单位时,y平均增加5个单位;
③设具有相关关系的两个变量的相关系数为r,则越接近于0,x和y之间的线性相关程度越强;
④在一个列联表中,由计算得的值,则的值越大,判断两个变量间有关联的把握就越大.
以上错误结论的个数为( )
A. 0 B. 1 C. 2 D. 3
2.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若的观测值为,我们有的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
B.从独立性检验可知有的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有的可能患有肺病
C.若从统计量中求出有的把握认为吸烟与患肺病有关系,是指有的可能性使得推断出现错误
D.以上三种说法都不正确
3.在一次独立性检验中,得出列联表如下:
合计
200
800
1 000
180
a
合计
380
且最后发现,两个分类变量和没有任何关系,则a的可能值是( )
A.200 B.720 C.100 D.180
4.以下三个命题中真命题的个数为( )
①对于分类变量X与Y的随机变量的观测值k来说,k越大,“X与Y有关系”的把握程度越大;
②回归直线恒过样本点的中心,且有可能不过任何一个样本点;
③2,1,3,2,3,3这组数据的中位数是.
A.0 B.1 C.2 D.3
5.在对某小学的学生进行性别与吃零食的调查中,得到下表数据:
吃零食
不吃零食
合计
男学生
24
31
55
女学生
8
26
34
合计
32
57
89
根据上述数据分析可得出的结论是( )
A.认为男女学生与吃零食与否有关系 B.认为男女学生与吃零食与否没有关系
C.性别不同决定了吃零食与否 D.以上都是错误的
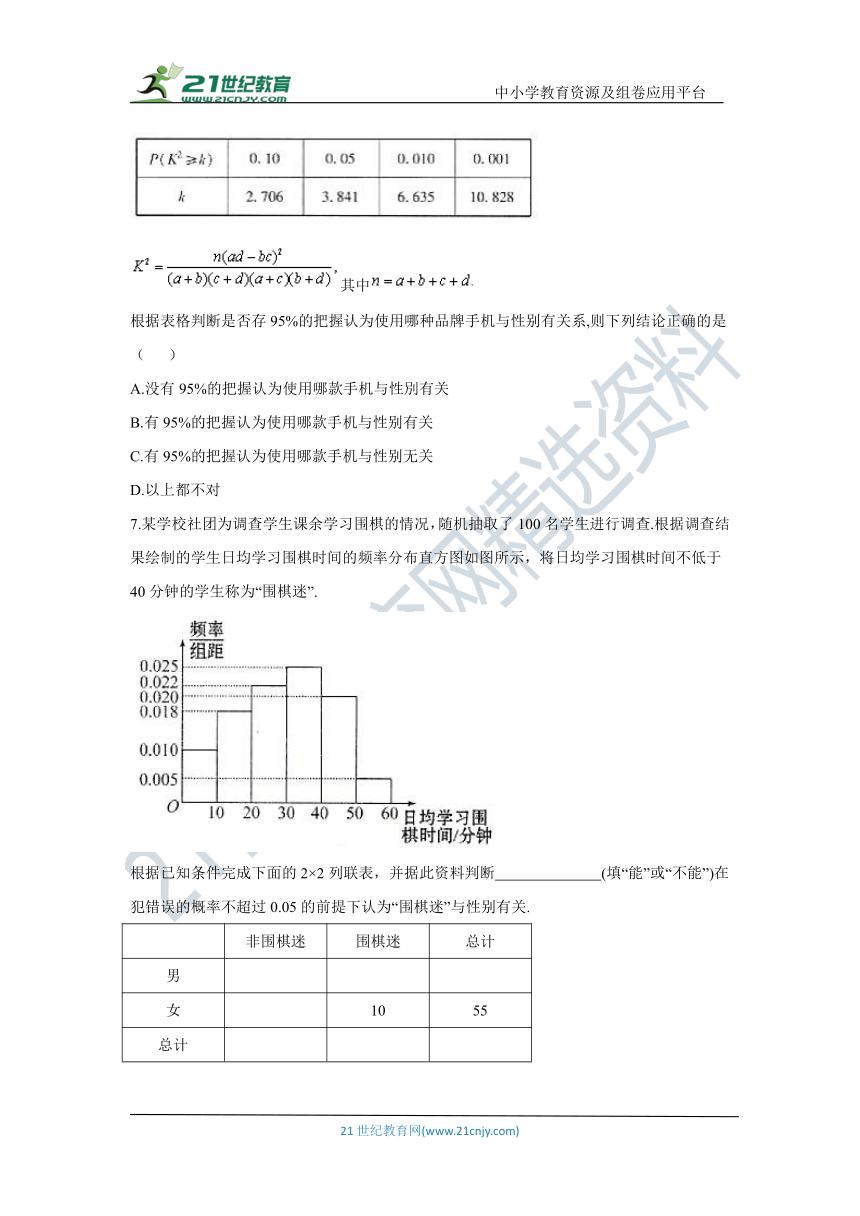
6.2018年,国际权威机构IDC发布的第二季度全球手机销售报告显示:华为突破2亿台出货量超越苹果的出货量,首次成为全球第二,华为无愧于中国最强的高科技企业.华为业务CEO余承东明确表示,华为的目标,就是在2021年前,成为全球最大的手机厂商.为了解华为手机和苹果手机使用的情况是否和消费者的性別有关,对100名华为手机使用者和苹果手机使用者进行统计,统计结果如下表:
附:
其中
根据表格判断是否存95%的把握认为使用哪种品牌手机与性别有关系,则下列结论正确的是( )
A.没有95%的把握认为使用哪款手机与性別有关
B.有95%的把握认为使用哪款手机与性别有关
C.有95%的把握认为使用哪款手机与性别无关
D.以上都不对
7.某学校社团为调查学生课余学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图如图所示,将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
根据已知条件完成下面的2×2列联表,并据此资料判断 (填“能”或“不能”)在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关.
非围棋迷
围棋迷
总计
男
女
10
55
总计
附:,其中.
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
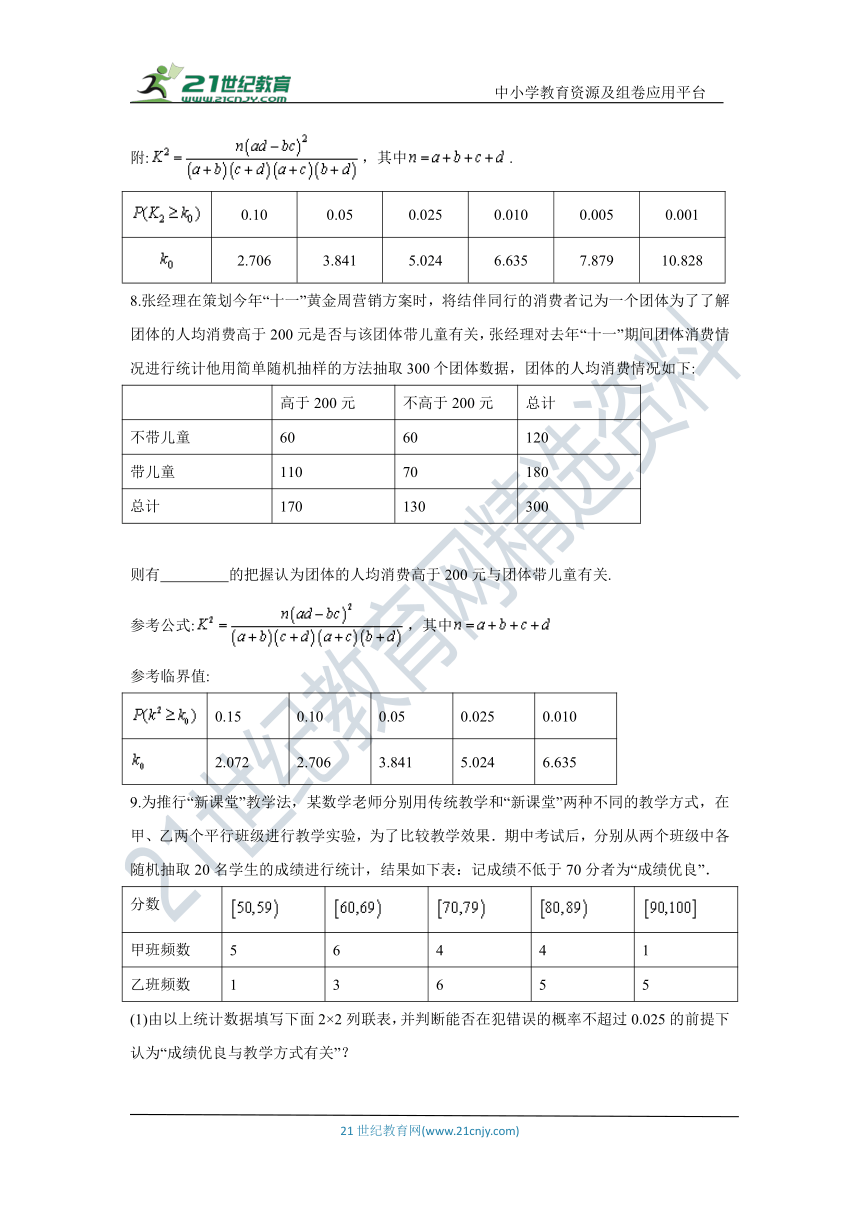
8.张经理在策划今年“十一”黄金周营销方案时,将结伴同行的消费者记为一个团体为了了解团体的人均消费高于200元是否与该团体带儿童有关,张经理对去年“十一”期间团体消费情况进行统计他用简单随机抽样的方法抽取300个团体数据,团体的人均消费情况如下:
高于200元
不高于200元
总计
不带儿童
60
60
120
带儿童
110
70
180
总计
170
130
300
则有 的把握认为团体的人均消费高于200元与团体带儿童有关.
参考公式:,其中
参考临界值:
0.15
0.10
0.05
0.025
0.010
2.072
2.706
3.841
5.024
6.635
9.为推行“新课堂”教学法,某数学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果.期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数
甲班频数
5
6
4
4
1
乙班频数
1
3
6
5
5
(1)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
甲班
乙班
总计
成绩优良
成绩不优良
总计
附:,其中
临界值表:
0.10
0.05
0.025
0.010
2.706
3.841
5.024
6.635
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为,求的分布列及数学期望.
答案以及解析
1.答案:C
解析:①根据方差公式,将一组数据中的每一个数据都加上或减去同一个常数后,方差不变,故①正确;②设一个线性回归方程,变量x增加1个单位时,y平均减少5个单位,故②不正确;③设具有相关关系的两个变量x,y的相关系数为r,则越接近于0,x和y之间的线性相关程度越弱,故③不正确;④在一个列联表中,由计算得的值,则的值越大,判断两个变量间有关联的把握就越大,故④正确.
其中错误的个数是2个.
故选C.
2.答案:C
解析:若的观测值为,我们有的把握认为吸烟与患肺病有关系,而不是在100个吸烟的人中必有99人患有肺病,故A不正确;从独立性检验可知有的把握认为吸烟与患肺病有关系时,并不是吸烟的人就有的可能患有肺病,故B不正确;若从统计量中求出有的把握认为吸烟与患肺病有关系,是指有的可能性使得推断出现错误,C正确.故选C.
3.答案:B
解析:和没有任何关系,也就是说,对应的比例和基本相等,
根据列联表可得和基本相等,检验可知,B满足条件.
故选B.
4.答案:D
解析:对于①,对于分类变量X与Y的随机变量的观测值k来说,k越大,“X与Y有关系”的把握程度越大,故①正确;
对于②,回归直线恒过样本点的中心,可以不过任何一个样本点,故②正确;
对于③,将这组数据按从小到大的顺序排列为1,2,2,3,3,3,则这组数据的中位数是,故③正确.故选D.
5.答案:A
解析:∵
.
∴有90%的把握认为男女学生与吃零食与否有关系.
6.答案:A
解析:由表可知
则
故没有95%的把握认为使用哪款手机与性别有关,故选A.
7.答案:不能
解析:由频率分布直方图可知,在抽取的100人中,“围棋迷”有人,
从而列联表如下所示:
非围棋迷
围棋迷
总计
男
30
15
45
女
45
10
55
总计
75
25
100
将列联表中的数据代入公式计算,得的观测值,
因为,所以不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关.
8.答案:90%
解析:由公式计算,得.
,有90%的把握认为团体的人均消费高于200元与团体带儿童有关.
9.答案:(1)由统计数据得列联表:
甲班
乙班
总计
成绩优良
9
16
25
成绩不优良
11
4
15
总计
20
20
40
根据列联表中的数据,得的观测值为
所以能在犯错概率不超过的前提下认为“成绩优良与教学方式有关”.
(2)由表可知在8人中成绩不优良的人数为,则的可能取值为
;
;所以的分布列为:
0
1
2
3
所以.
1.下列说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;②设有一个线性回归方程,变量x增加1个单位时,y平均增加5个单位;
③设具有相关关系的两个变量的相关系数为r,则越接近于0,x和y之间的线性相关程度越强;
④在一个列联表中,由计算得的值,则的值越大,判断两个变量间有关联的把握就越大.
以上错误结论的个数为( )
A. 0 B. 1 C. 2 D. 3
2.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若的观测值为,我们有的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
B.从独立性检验可知有的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有的可能患有肺病
C.若从统计量中求出有的把握认为吸烟与患肺病有关系,是指有的可能性使得推断出现错误
D.以上三种说法都不正确
3.在一次独立性检验中,得出列联表如下:
合计
200
800
1 000
180
a
合计
380
且最后发现,两个分类变量和没有任何关系,则a的可能值是( )
A.200 B.720 C.100 D.180
4.以下三个命题中真命题的个数为( )
①对于分类变量X与Y的随机变量的观测值k来说,k越大,“X与Y有关系”的把握程度越大;
②回归直线恒过样本点的中心,且有可能不过任何一个样本点;
③2,1,3,2,3,3这组数据的中位数是.
A.0 B.1 C.2 D.3
5.在对某小学的学生进行性别与吃零食的调查中,得到下表数据:
吃零食
不吃零食
合计
男学生
24
31
55
女学生
8
26
34
合计
32
57
89
根据上述数据分析可得出的结论是( )
A.认为男女学生与吃零食与否有关系 B.认为男女学生与吃零食与否没有关系
C.性别不同决定了吃零食与否 D.以上都是错误的
6.2018年,国际权威机构IDC发布的第二季度全球手机销售报告显示:华为突破2亿台出货量超越苹果的出货量,首次成为全球第二,华为无愧于中国最强的高科技企业.华为业务CEO余承东明确表示,华为的目标,就是在2021年前,成为全球最大的手机厂商.为了解华为手机和苹果手机使用的情况是否和消费者的性別有关,对100名华为手机使用者和苹果手机使用者进行统计,统计结果如下表:
附:
其中
根据表格判断是否存95%的把握认为使用哪种品牌手机与性别有关系,则下列结论正确的是( )
A.没有95%的把握认为使用哪款手机与性別有关
B.有95%的把握认为使用哪款手机与性别有关
C.有95%的把握认为使用哪款手机与性别无关
D.以上都不对
7.某学校社团为调查学生课余学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图如图所示,将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
根据已知条件完成下面的2×2列联表,并据此资料判断 (填“能”或“不能”)在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关.
非围棋迷
围棋迷
总计
男
女
10
55
总计
附:,其中.
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
8.张经理在策划今年“十一”黄金周营销方案时,将结伴同行的消费者记为一个团体为了了解团体的人均消费高于200元是否与该团体带儿童有关,张经理对去年“十一”期间团体消费情况进行统计他用简单随机抽样的方法抽取300个团体数据,团体的人均消费情况如下:
高于200元
不高于200元
总计
不带儿童
60
60
120
带儿童
110
70
180
总计
170
130
300
则有 的把握认为团体的人均消费高于200元与团体带儿童有关.
参考公式:,其中
参考临界值:
0.15
0.10
0.05
0.025
0.010
2.072
2.706
3.841
5.024
6.635
9.为推行“新课堂”教学法,某数学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果.期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数
甲班频数
5
6
4
4
1
乙班频数
1
3
6
5
5
(1)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
甲班
乙班
总计
成绩优良
成绩不优良
总计
附:,其中
临界值表:
0.10
0.05
0.025
0.010
2.706
3.841
5.024
6.635
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为,求的分布列及数学期望.
答案以及解析
1.答案:C
解析:①根据方差公式,将一组数据中的每一个数据都加上或减去同一个常数后,方差不变,故①正确;②设一个线性回归方程,变量x增加1个单位时,y平均减少5个单位,故②不正确;③设具有相关关系的两个变量x,y的相关系数为r,则越接近于0,x和y之间的线性相关程度越弱,故③不正确;④在一个列联表中,由计算得的值,则的值越大,判断两个变量间有关联的把握就越大,故④正确.
其中错误的个数是2个.
故选C.
2.答案:C
解析:若的观测值为,我们有的把握认为吸烟与患肺病有关系,而不是在100个吸烟的人中必有99人患有肺病,故A不正确;从独立性检验可知有的把握认为吸烟与患肺病有关系时,并不是吸烟的人就有的可能患有肺病,故B不正确;若从统计量中求出有的把握认为吸烟与患肺病有关系,是指有的可能性使得推断出现错误,C正确.故选C.
3.答案:B
解析:和没有任何关系,也就是说,对应的比例和基本相等,
根据列联表可得和基本相等,检验可知,B满足条件.
故选B.
4.答案:D
解析:对于①,对于分类变量X与Y的随机变量的观测值k来说,k越大,“X与Y有关系”的把握程度越大,故①正确;
对于②,回归直线恒过样本点的中心,可以不过任何一个样本点,故②正确;
对于③,将这组数据按从小到大的顺序排列为1,2,2,3,3,3,则这组数据的中位数是,故③正确.故选D.
5.答案:A
解析:∵
.
∴有90%的把握认为男女学生与吃零食与否有关系.
6.答案:A
解析:由表可知
则
故没有95%的把握认为使用哪款手机与性别有关,故选A.
7.答案:不能
解析:由频率分布直方图可知,在抽取的100人中,“围棋迷”有人,
从而列联表如下所示:
非围棋迷
围棋迷
总计
男
30
15
45
女
45
10
55
总计
75
25
100
将列联表中的数据代入公式计算,得的观测值,
因为,所以不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关.
8.答案:90%
解析:由公式计算,得.
,有90%的把握认为团体的人均消费高于200元与团体带儿童有关.
9.答案:(1)由统计数据得列联表:
甲班
乙班
总计
成绩优良
9
16
25
成绩不优良
11
4
15
总计
20
20
40
根据列联表中的数据,得的观测值为
所以能在犯错概率不超过的前提下认为“成绩优良与教学方式有关”.
(2)由表可知在8人中成绩不优良的人数为,则的可能取值为
;
;所以的分布列为:
0
1
2
3
所以.
