鲁科版(2019)高中物理 选择性必修第三册 课时分层作业4 气体实验定律word版含答案
文档属性
| 名称 | 鲁科版(2019)高中物理 选择性必修第三册 课时分层作业4 气体实验定律word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-01 17:01:00 | ||
图片预览


文档简介
课时分层作业(四) 气体实验定律
(建议用时:25分钟)
◎考点一 气体的等温变化
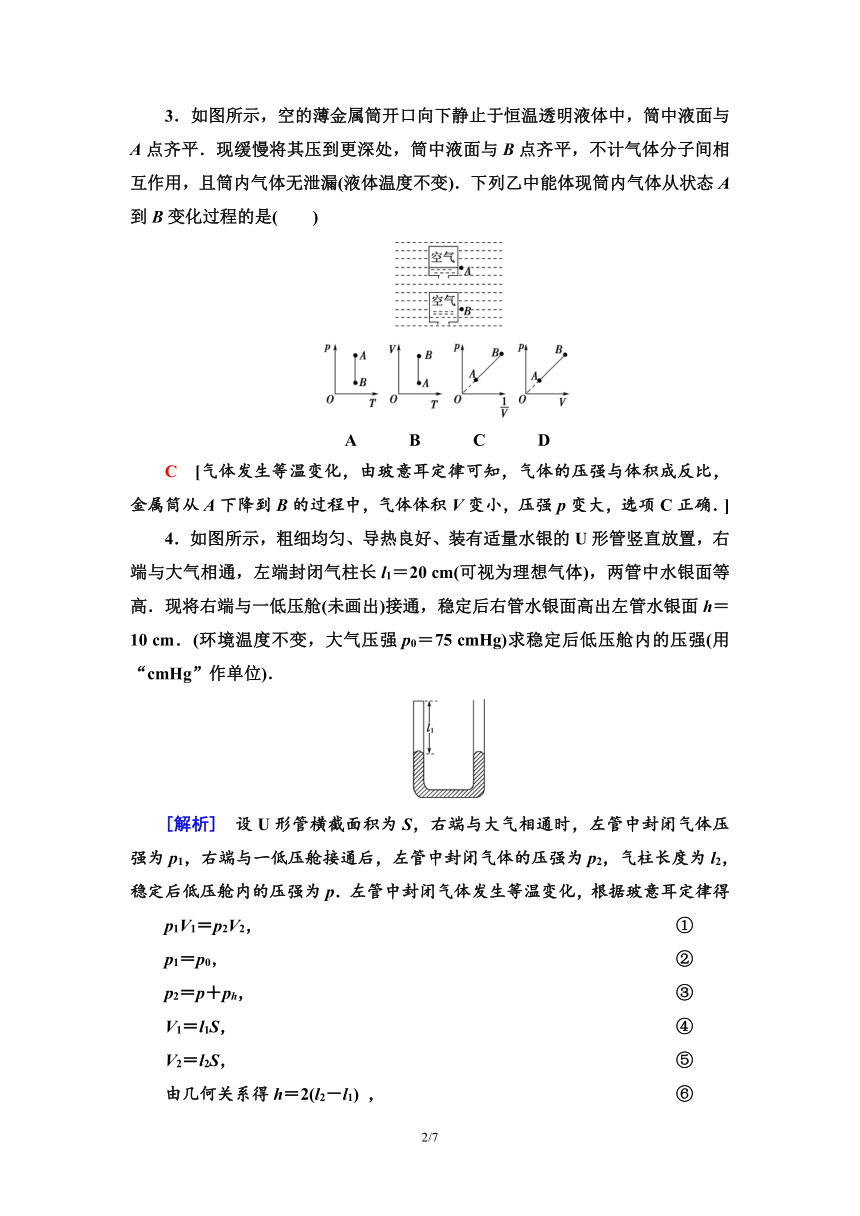
1.(多选)如图所示,某种自动洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器知管中的空气压力,从而控制进水量.设温度不变,洗衣缸内水位升高,则细管中被封闭空气的下列说法不正确的是( )
A.体积不变,压强变小 B.体积变小,压强变大
C.体积不变,压强变大 D.体积变小,压强变小
ACD [当水位升高时,细管中的水位也升高,被封闭空气的体积减小,由玻意耳定律可知,压强增大,B正确.所以不正确的选A、C、D.]
2.(多选)如图所示,水银柱上面封闭一段气体,管内外水银面高度差h=72 cm,大气压强为76 cmHg,下列说法不正确的是( )
A.将管稍微上提,h不变
B.将管稍微上提,h变大
C.将管下插至管顶与管外水银面高度差为70 cm时,管内外水银面高度差也是70 cm
D.将管下插至C项所述位置时,管内外水银面高度差小于70 cm
AC [由p·V=C知上提体积变大,压强变小,内外液面差变大,B对.同样下插时,体积变小,压强变大,内外液面差变小,D对.]
3.如图所示,空的薄金属筒开口向下静止于恒温透明液体中,筒中液面与A点齐平.现缓慢将其压到更深处,筒中液面与B点齐平,不计气体分子间相互作用,且筒内气体无泄漏(液体温度不变).下列乙中能体现筒内气体从状态A到B变化过程的是( )
A B C D
C [气体发生等温变化,由玻意耳定律可知,气体的压强与体积成反比,金属筒从A下降到B的过程中,气体体积V变小,压强p变大,选项C正确.]
4.如图所示,粗细均匀、导热良好、装有适量水银的U形管竖直放置,右端与大气相通,左端封闭气柱长l1=20 cm(可视为理想气体),两管中水银面等高.现将右端与一低压舱(未画出)接通,稳定后右管水银面高出左管水银面h=10 cm.(环境温度不变,大气压强p0=75 cmHg)求稳定后低压舱内的压强(用“cmHg”作单位).
[解析] 设U形管横截面积为S,右端与大气相通时,左管中封闭气体压强为p1,右端与一低压舱接通后,左管中封闭气体的压强为p2,气柱长度为l2,稳定后低压舱内的压强为p.左管中封闭气体发生等温变化,根据玻意耳定律得
p1V1=p2V2, ①
p1=p0, ②
p2=p+ph, ③
V1=l1S, ④
V2=l2S, ⑤
由几何关系得h=2(l2-l1) , ⑥
联立①②③④⑤⑥式,代入数据得p=50 cmHg.
[答案] 50 cmHg
◎考点二 气体的等容变化
5.某同学家一台新电冰箱能显示冷藏室内的温度,存放食物之前该同学进行试通电,该同学将打开的冰箱密封门关闭并给冰箱通电.若大气压为1.0×105 Pa,刚通电时显示温度为27 ℃,通电一段时间后显示温度为7 ℃,则此时密封的冷藏室中气体的压强是( )
A.0.26×105 Pa B.0.93×105 Pa
C.1.07×105 Pa D.3.86×105 Pa
B [冷藏室气体的初状态:T1=(273+27)K=300 K,p1=1×105 Pa,末状态:T2=(273+7)K=280 K,压强为p2,气体体积不变,根据查理定律得:= ,代入数据得:p2≈0.93×105 Pa.]
6.一定质量的气体,在体积不变的情况下,温度由0 ℃升高到10 ℃时,其压强的增加量为Δp1,当它由100 ℃升高到110 ℃时,其压强的增加量为Δp2,则Δp1与Δp2之比是( )
A.1∶1 B.1∶10
C.10∶1 D.10∶110
A [等容变化,这四个状态在同一条等容线上,因Δt相同,所以Δp也相同,故A正确.]
7.用易拉罐盛装碳酸饮料非常卫生和方便,但如果剧烈碰撞或严重受热会导致爆炸.我们通常用的可乐易拉罐容积V=355 mL.假设在室温(17 ℃)下罐内装有0.9V的饮料,剩余空间充满CO2气体,气体压强为1 atm.若易拉罐能承受的最大压强为1.2 atm,则保存温度不能超过多少?
[解析] 取CO2气体为研究对象,则:
初态:p1=1 atm,T1=(273+17)K=290 K,
末态:p2=1.2 atm,T2=?.
气体发生等容变化,
由查理定律=得
T2=T1=K=348 K,
t=(348-273) ℃=75 ℃.
[答案] 75 ℃
◎考点三 气体的等压变化
8.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,改变的量有( )
A.活塞高度h
B.汽缸高度H
C.气体压强p
D.弹簧长度L
B [以汽缸整体为研究对象,由受力平衡知弹簧弹力等于总重力,故L、h不变,设缸壁的重力为G1,则封闭气体的压强p=p0-保持不变,当温度升高时,由盖—吕萨克定律知气体体积增大,H将减小,故只有B项正确.]
9.如图所示,静止在地面上的汽缸中封闭着温度为100 ℃的空气,一重物用绳索经滑轮跟汽缸中活塞相连接,重物和活塞都处于平衡状态,这时活塞离汽缸底的高度为10 cm.如果缸内空气变为0 ℃,重物将上升多少厘米?
[解析] 汽缸中气体发生的是等压变化,
初状态:V1=10S,T1=373 K;
末状态:V2=lS,T2=273 K.
由=得V2≈7.32S,
即活塞到缸底的距离为7.32 cm,
所以重物将上升Δl=(10-7.32)cm=2.68 cm.
[答案] 2.68 cm
(建议用时:15分钟)
10.活塞式抽气机汽缸容积为V,用它给容积为2V的容器抽气,抽气机抽动两次(抽气过程可视为等温变化),容器内剩余气体压强是原来的( )
A. B.
C. D.
C [设容器内气体压强为p,则气体状态参量为
p1=p,V1=2V,V2=3V,第一次抽气过程,由玻意耳定律得
p1V1=p2V2,即p×2V=p2×3V,
解得p2=p;
第二次抽气过程,气体状态参量
p2=p,V2′=2V,V3=3V,
由玻意耳定律得p2V2′=p3V3,
即p×2V=p3×3V,
解得p3=p.]
11.(多选)如图所示,四支两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开,按图中标明的条件,当玻璃管水平放置时,水银柱处于静止状态.如果管内两端的空气都升高相同的温度,则水银柱向左移动的是( )
CD [假设升温后,水银柱不动,则两边压强要增加,由查理定律有,压强的增加量Δp=,而各管原压强p相同,所以Δp∝,即T高,Δp小,也就可以确定水银柱应向温度高的方向移动,故C、D项正确.]
12.如图所示,容积为V的汽缸由导热材料制成,面积为S的活塞将汽缸分成容积相等的上下两部分,汽缸上部通过细管与装有某种液体的容器相连,细管上有一阀门K.开始时,K关闭,汽缸内上下两部分气体的压强均为p0.现将K打开,容器内的液体缓慢地流入汽缸,当流入的液体体积为时,将K关闭,活塞平衡时其下方气体的体积减小了.不计活塞的质量和体积,外界温度保持不变,重力加速度大小为g.求流入汽缸内液体的质量.
[解析] 设活塞再次平衡后,活塞上方气体的体积为V1,压强为p1;下方气体的体积为V2,压强为p2.在活塞下移的过程中,活塞上、下方气体的温度均保持不变,由玻意耳定律得
p0=p1V1,
p0=p2V2,
由已知条件得
V1=+-=V,
V2=-=,
设活塞上方液体的质量为m,由力的平衡条件得
p2S=p1S+mg,
联立以上各式得m=.
[答案]
13.容积为2 L的烧瓶,在压强为1.0×105 Pa时,用塞子塞住瓶口,此时温度为27 ℃,当把它加热到127 ℃时,塞子被弹开,稍过一会儿,重新把塞子塞好,停止加热并使它逐渐降温到27 ℃,求:
(1)塞子弹开前的最大压强;
(2)27 ℃时剩余空气的压强.
[解析] 塞子弹开前,瓶内气体的状态变化为等容变化.塞子打开后,瓶内有部分气体会逸出,此后应选择瓶中剩余气体为研究对象,再利用查理定律求解.
(1)塞子打开前,选瓶中气体为研究对象:
初态:p1=1.0×105 Pa,T1=(273+27) K=300 K,
末态:p2=?T2=(273+127) K=400 K,
由查理定律可得
p2== Pa
≈1.33×105 Pa.
(2)塞子塞紧后,选瓶中剩余气体为研究对象:
初态:p1′=1.0×105 Pa,T1′=400 K,
末态:p2′=?,T2′=300 K,
由查理定律可得
p2′==Pa≈7.5×104 Pa.
[答案] (1)1.33×105 Pa (2)7.5×104 Pa
7/7
(建议用时:25分钟)
◎考点一 气体的等温变化
1.(多选)如图所示,某种自动洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器知管中的空气压力,从而控制进水量.设温度不变,洗衣缸内水位升高,则细管中被封闭空气的下列说法不正确的是( )
A.体积不变,压强变小 B.体积变小,压强变大
C.体积不变,压强变大 D.体积变小,压强变小
ACD [当水位升高时,细管中的水位也升高,被封闭空气的体积减小,由玻意耳定律可知,压强增大,B正确.所以不正确的选A、C、D.]
2.(多选)如图所示,水银柱上面封闭一段气体,管内外水银面高度差h=72 cm,大气压强为76 cmHg,下列说法不正确的是( )
A.将管稍微上提,h不变
B.将管稍微上提,h变大
C.将管下插至管顶与管外水银面高度差为70 cm时,管内外水银面高度差也是70 cm
D.将管下插至C项所述位置时,管内外水银面高度差小于70 cm
AC [由p·V=C知上提体积变大,压强变小,内外液面差变大,B对.同样下插时,体积变小,压强变大,内外液面差变小,D对.]
3.如图所示,空的薄金属筒开口向下静止于恒温透明液体中,筒中液面与A点齐平.现缓慢将其压到更深处,筒中液面与B点齐平,不计气体分子间相互作用,且筒内气体无泄漏(液体温度不变).下列乙中能体现筒内气体从状态A到B变化过程的是( )
A B C D
C [气体发生等温变化,由玻意耳定律可知,气体的压强与体积成反比,金属筒从A下降到B的过程中,气体体积V变小,压强p变大,选项C正确.]
4.如图所示,粗细均匀、导热良好、装有适量水银的U形管竖直放置,右端与大气相通,左端封闭气柱长l1=20 cm(可视为理想气体),两管中水银面等高.现将右端与一低压舱(未画出)接通,稳定后右管水银面高出左管水银面h=10 cm.(环境温度不变,大气压强p0=75 cmHg)求稳定后低压舱内的压强(用“cmHg”作单位).
[解析] 设U形管横截面积为S,右端与大气相通时,左管中封闭气体压强为p1,右端与一低压舱接通后,左管中封闭气体的压强为p2,气柱长度为l2,稳定后低压舱内的压强为p.左管中封闭气体发生等温变化,根据玻意耳定律得
p1V1=p2V2, ①
p1=p0, ②
p2=p+ph, ③
V1=l1S, ④
V2=l2S, ⑤
由几何关系得h=2(l2-l1) , ⑥
联立①②③④⑤⑥式,代入数据得p=50 cmHg.
[答案] 50 cmHg
◎考点二 气体的等容变化
5.某同学家一台新电冰箱能显示冷藏室内的温度,存放食物之前该同学进行试通电,该同学将打开的冰箱密封门关闭并给冰箱通电.若大气压为1.0×105 Pa,刚通电时显示温度为27 ℃,通电一段时间后显示温度为7 ℃,则此时密封的冷藏室中气体的压强是( )
A.0.26×105 Pa B.0.93×105 Pa
C.1.07×105 Pa D.3.86×105 Pa
B [冷藏室气体的初状态:T1=(273+27)K=300 K,p1=1×105 Pa,末状态:T2=(273+7)K=280 K,压强为p2,气体体积不变,根据查理定律得:= ,代入数据得:p2≈0.93×105 Pa.]
6.一定质量的气体,在体积不变的情况下,温度由0 ℃升高到10 ℃时,其压强的增加量为Δp1,当它由100 ℃升高到110 ℃时,其压强的增加量为Δp2,则Δp1与Δp2之比是( )
A.1∶1 B.1∶10
C.10∶1 D.10∶110
A [等容变化,这四个状态在同一条等容线上,因Δt相同,所以Δp也相同,故A正确.]
7.用易拉罐盛装碳酸饮料非常卫生和方便,但如果剧烈碰撞或严重受热会导致爆炸.我们通常用的可乐易拉罐容积V=355 mL.假设在室温(17 ℃)下罐内装有0.9V的饮料,剩余空间充满CO2气体,气体压强为1 atm.若易拉罐能承受的最大压强为1.2 atm,则保存温度不能超过多少?
[解析] 取CO2气体为研究对象,则:
初态:p1=1 atm,T1=(273+17)K=290 K,
末态:p2=1.2 atm,T2=?.
气体发生等容变化,
由查理定律=得
T2=T1=K=348 K,
t=(348-273) ℃=75 ℃.
[答案] 75 ℃
◎考点三 气体的等压变化
8.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,改变的量有( )
A.活塞高度h
B.汽缸高度H
C.气体压强p
D.弹簧长度L
B [以汽缸整体为研究对象,由受力平衡知弹簧弹力等于总重力,故L、h不变,设缸壁的重力为G1,则封闭气体的压强p=p0-保持不变,当温度升高时,由盖—吕萨克定律知气体体积增大,H将减小,故只有B项正确.]
9.如图所示,静止在地面上的汽缸中封闭着温度为100 ℃的空气,一重物用绳索经滑轮跟汽缸中活塞相连接,重物和活塞都处于平衡状态,这时活塞离汽缸底的高度为10 cm.如果缸内空气变为0 ℃,重物将上升多少厘米?
[解析] 汽缸中气体发生的是等压变化,
初状态:V1=10S,T1=373 K;
末状态:V2=lS,T2=273 K.
由=得V2≈7.32S,
即活塞到缸底的距离为7.32 cm,
所以重物将上升Δl=(10-7.32)cm=2.68 cm.
[答案] 2.68 cm
(建议用时:15分钟)
10.活塞式抽气机汽缸容积为V,用它给容积为2V的容器抽气,抽气机抽动两次(抽气过程可视为等温变化),容器内剩余气体压强是原来的( )
A. B.
C. D.
C [设容器内气体压强为p,则气体状态参量为
p1=p,V1=2V,V2=3V,第一次抽气过程,由玻意耳定律得
p1V1=p2V2,即p×2V=p2×3V,
解得p2=p;
第二次抽气过程,气体状态参量
p2=p,V2′=2V,V3=3V,
由玻意耳定律得p2V2′=p3V3,
即p×2V=p3×3V,
解得p3=p.]
11.(多选)如图所示,四支两端封闭、粗细均匀的玻璃管内的空气被一段水银柱隔开,按图中标明的条件,当玻璃管水平放置时,水银柱处于静止状态.如果管内两端的空气都升高相同的温度,则水银柱向左移动的是( )
CD [假设升温后,水银柱不动,则两边压强要增加,由查理定律有,压强的增加量Δp=,而各管原压强p相同,所以Δp∝,即T高,Δp小,也就可以确定水银柱应向温度高的方向移动,故C、D项正确.]
12.如图所示,容积为V的汽缸由导热材料制成,面积为S的活塞将汽缸分成容积相等的上下两部分,汽缸上部通过细管与装有某种液体的容器相连,细管上有一阀门K.开始时,K关闭,汽缸内上下两部分气体的压强均为p0.现将K打开,容器内的液体缓慢地流入汽缸,当流入的液体体积为时,将K关闭,活塞平衡时其下方气体的体积减小了.不计活塞的质量和体积,外界温度保持不变,重力加速度大小为g.求流入汽缸内液体的质量.
[解析] 设活塞再次平衡后,活塞上方气体的体积为V1,压强为p1;下方气体的体积为V2,压强为p2.在活塞下移的过程中,活塞上、下方气体的温度均保持不变,由玻意耳定律得
p0=p1V1,
p0=p2V2,
由已知条件得
V1=+-=V,
V2=-=,
设活塞上方液体的质量为m,由力的平衡条件得
p2S=p1S+mg,
联立以上各式得m=.
[答案]
13.容积为2 L的烧瓶,在压强为1.0×105 Pa时,用塞子塞住瓶口,此时温度为27 ℃,当把它加热到127 ℃时,塞子被弹开,稍过一会儿,重新把塞子塞好,停止加热并使它逐渐降温到27 ℃,求:
(1)塞子弹开前的最大压强;
(2)27 ℃时剩余空气的压强.
[解析] 塞子弹开前,瓶内气体的状态变化为等容变化.塞子打开后,瓶内有部分气体会逸出,此后应选择瓶中剩余气体为研究对象,再利用查理定律求解.
(1)塞子打开前,选瓶中气体为研究对象:
初态:p1=1.0×105 Pa,T1=(273+27) K=300 K,
末态:p2=?T2=(273+127) K=400 K,
由查理定律可得
p2== Pa
≈1.33×105 Pa.
(2)塞子塞紧后,选瓶中剩余气体为研究对象:
初态:p1′=1.0×105 Pa,T1′=400 K,
末态:p2′=?,T2′=300 K,
由查理定律可得
p2′==Pa≈7.5×104 Pa.
[答案] (1)1.33×105 Pa (2)7.5×104 Pa
7/7
同课章节目录
- 第1章 分子动理论与气体实验定律
- 第1节 分子动理论的基本观点
- 第2节 科学测量:用油膜法估测油酸分子的大小
- 第3节 气体分子速率分布的统计规律
- 第4节 科学探究:气体压强与体积的关系
- 第5节 气体实验定律
- 第2章 固体与液体
- 第1节 固体类型及微观结构
- 第2节 表面张力和毛细现象
- 第3节 材料及其应用
- 第3章 热力学定律
- 第1节 热力学第一定律
- 第2节 能量的转化与守恒
- 第3节 热力学第二定律
- 第4节 熵——系统无序程度的量度
- 第4章 原子结构
- 第1节 电子的发现与汤姆孙原子模型
- 第2节 原子的核式结构模型
- 第3节 光谱与氢原子光谱
- 第4节 玻尔原子模型
- 第5章 原子核与核能
- 第1节 认识原子核
- 第2节 原子核衰变及半衰期
- 第3节 核力与核能
- 第4节 核裂变和核聚变
- 第5节 核能的利用与环境保护
- 第6章 波粒二象性
- 第1节 光电效应及其解释
- 第2节 实物粒子的波粒二象性
