初中数学沪教版八年级下册第二十章第三节 一次函数的应用寒假预习练习题(Word版 含解析)
文档属性
| 名称 | 初中数学沪教版八年级下册第二十章第三节 一次函数的应用寒假预习练习题(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 182.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览



文档简介
初中数学上教版八年级下册第二十章第三节寒假预习练习题
一、选择题
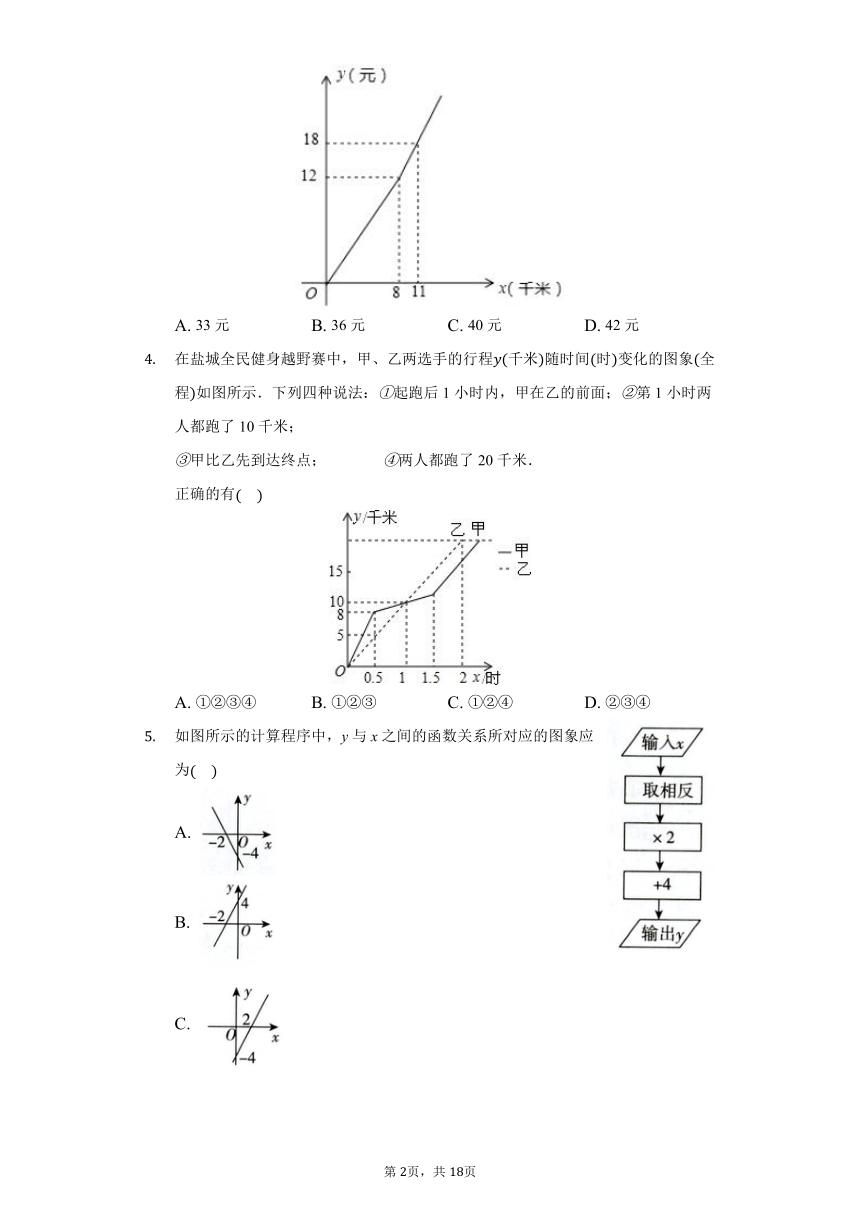
为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润万元与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是.
A.
4月份的利润为50万元
B.
治污改造完成后每月利润比前一个月增加30万元
C.
治污改造完成前后共有4个月的利润低于100万元
D.
9月份该厂利润达到200万元
A,B两地相距30km,甲乙两人沿同一条路线从A地到B地如图,反映的是两人行进路程与行进时间之间的关系,甲始终是匀速行进,乙的行进不是匀速的;乙用了5个小时到达目的地;乙比甲迟出发小时;甲在出发5小时后被乙追上以上说法正确的个数有
A.
1个
B.
2个
C.
3个
D.
4个
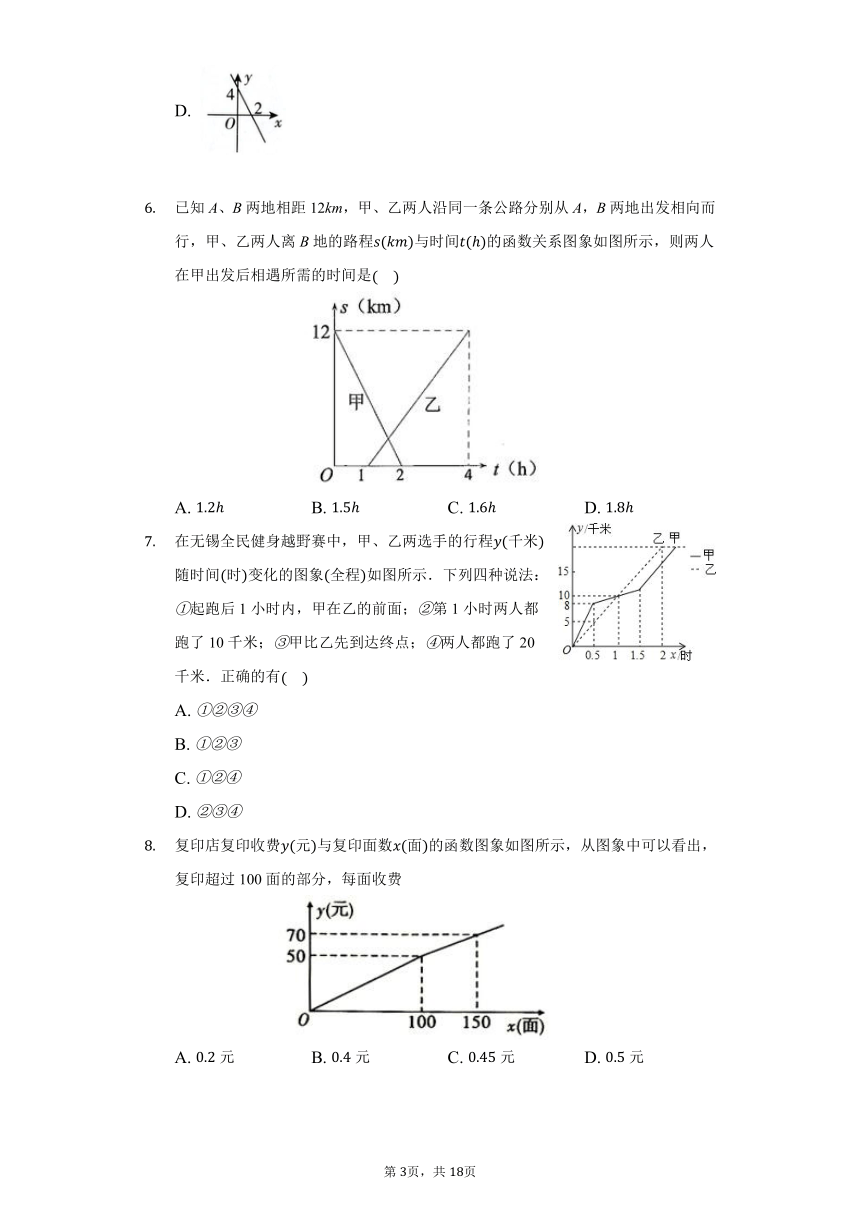
随着“互联网”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用单位:元与行驶里程单位:千米的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为?
A.
33元
B.
36元
C.
40元
D.
42元
在盐城全民健身越野赛中,甲、乙两选手的行程千米随时间时变化的图象全程如图所示.下列四种说法:起跑后1小时内,甲在乙的前面;第1小时两人都跑了10千米;
甲比乙先到达终点;???????????????两人都跑了20千米.
正确的有
A.
B.
C.
D.
如图所示的计算程序中,y与x之间的函数关系所对应的图象应为
A.
B.
C.
D.
已知A、B两地相距12km,甲、乙两人沿同一条公路分别从A,B两地出发相向而行,甲、乙两人离B地的路程与时间的函数关系图象如图所示,则两人在甲出发后相遇所需的时间是
A.
B.
C.
D.
在无锡全民健身越野赛中,甲、乙两选手的行程千米随时间时变化的图象全程如图所示.下列四种说法:起跑后1小时内,甲在乙的前面;第1小时两人都跑了10千米;甲比乙先到达终点;两人都跑了20千米.正确的有
A.
B.
C.
D.
复印店复印收费元与复印面数面的函数图象如图所示,从图象中可以看出,复印超过100面的部分,每面收费
A.
元
B.
元
C.
元
D.
元
一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量与时间之间的关系如图所示,则每分钟的进水量与出水量分别是
A.
5
L,
B.
,5
L
C.
5
L,
D.
,5
L
药品研究所开发一种抗菌新药,经多年动物实验之后,首次用于临床人体试验,测得成人服药后血液中药物浓度微克毫升与服药后时间时之间的函数关系如图所示,则当时,y的取值范围是
A.
B.
C.
D.
某超市从元旦起,在20天内试销一种特种水果.试销期间的日销售量千克与销售时间天,销售单价元千克与销售时间天之间的函数图象如图所示.那么,下列说法正确的是?
?
?
?
A.
试销第10天的销售量为15千克
B.
试销期间日销售量不低于24千克的有4天
C.
试销第16天的销售单价为元千克
D.
试销第18天的销售额为100元
某超市从元旦起,在20天内试销一种特种水果.试销期间的日销售量千克与销售时间天,销售单价元千克与销售时间天之间的函数图象如图所示.那么,下列说法正确的是
A.
试销第10天的销售量为15千克
B.
试销期间日销售量不低于24千克的有4天
C.
试销第16天的销售单价为元千克
D.
试销第18天的销售额为100元
二、填空题
空气中传播的速度与气温之间的关系式为;当时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为______
已知一个长方形的长为5cm,宽为xcm,周长为ycm,则y与x之间的函数表达式为________.
声音在空气中传播的速度与气温之间在如下关系:当气温时,某人看到闪电5s后才听到声音光传播的时间忽略不计则此人与发生闪电所在地相距__________m.
小明正在参加学校运动会的百米赛跑,他距终点的路程米与他起跑时间秒之间的函数关系式为:,则自变量t的取值范围是________.
三、解答题
随着网络电商与快递行业的飞速发展,叠加疫情影响,越来越多的人选择网络购物.在暑期来临之际,天猫超市为了促销,推出了普通会员与VIP会员两种销售方式,普通会员的收费方式是:所购商品的金额不超过300元,客户还需支付快递费20元;如果所购商品的金额超过300元,则所购商品给予8折优惠,并免除20元的快递费,VIP会员的收费方式是:缴纳VIP会员费50元,所购商品给予折优惠,并免除20元的快递费.
请分别写出按普通会员、VIP会员购买商品应付的金额元与所购商品的金额元之间的函数关系式;
某网民计划在促销活动期间在天猫超市购买元的商品,则他应该选择哪种购买方式比较合算?
某市为了鼓励居民节约用水,决定实行两级收费制度.每月用水量不超过14吨含14吨的,按政府补贴优惠价m元吨收费;若每月用水量超过14吨,则超过部分按市场价n元吨收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
求每吨水的政府补贴优惠价和市场价分别是多少?
设每月用水量为吨,应交水费为y元,请写出y与x之间的函数关系式.
2020年新冠肺炎疫情在全球蔓延,全球疫情大考面前,中国始终同各国安危与共、风雨同舟,时至5月,中国已经向150多个国家和国际组织提供医疗物资援助.某次援助,我国组织20架飞机装运口罩、消毒剂、防护服三种医疗物资共120吨,按计划20架飞机都要装运,每架飞机只能装运同一种医疗物资,且必须装满.根据如下表提供的信息,解答以下问题:
防疫物资种类
口罩
消毒剂
防护服
每架飞机运载量吨
8
5
4
每吨物资运费元
1200
1600
1000
若有x架飞机装运口罩,有y架飞机装运消毒剂,求y与x之间的函数关系式;
若此次物资运费为W元,求W与x之间的函数关系式;
如果装运每种医疗物资的飞机都不少于4架,那么怎样安排运送物资,才能使此次物资运费最少,最少运费为多少元?
为迎接“国家卫生城市”复检,某市环卫局准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
每个A型垃圾箱和B型垃圾箱各多少元?
现需要购买A,B两种型号的垃圾箱共30个,设购买A型垃圾箱a个,购买A型垃圾箱和B型垃圾箱的总费用为w元,求w与a的函数表达式.如果购买A型垃圾箱的数量是B型垃圾箱数量的2倍,求购买A型垃圾箱和B型垃圾箱的总费用.
答案和解析
1.【答案】C
【解析】
【分析】
此题主要考查了一次函数与反比例函数的应用,正确得出函数解析式是解题关键.
直接利用已知点求出一次函数与反比例函数的解析式进而分别分析得出答案.
【解答】
解:设反比例函数的解析式为,
把代入得,,
反比例函数的解析式为:,
当时,,
月份的利润为50万元,故此选项正确,不合题意;
B.治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C.当时,则,
解得:,
设一次函数解析式为:,
则,
解得:,
故一次函数解析式为:,
当时,则,
则只有3月,4月,5月,共3个月的利润低于100万元,故此选项不正确,符合题意.
D.一次函数解析式为:,
故时,,
解得:,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选C.
2.【答案】B
【解析】解:由图象可得,
甲始终是匀速行进,乙的行进不是匀速的,故正确;
乙用了个小时到达目的地,故错误;
乙比甲迟出发小时,故正确;
甲在出发不到5小时后被乙追上,故错误;
故选:B.
根据题意和函数图象中的数据,可以判断各个小题中的结论是否正确,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
3.【答案】C
【解析】
【分析】
本题主要考查一次函数的图象与待定系数法求一次函数解析式,熟练掌握待定系数法求得一次函数解析式是解题的关键.
待定系数法求出时y关于x的函数解析式,再求出时y的值即可.
【解答】
解:当行驶里程时,设,
将、代入,得:,
解得:,
,
?当时,,
?如果小明某次打车行驶里程为22千米,则他的打车费用为40元.
故选C.
4.【答案】C
【解析】
【分析】
由图象可知起跑后1小时内,甲在乙的前面;在跑了1小时时,乙追上甲,此时都跑了10千米;乙比甲先到达终点;求得乙跑的直线的解析式,即可求得两人跑的距离,则可求得答案.此题考查了函数图形的意义解题的关键是根据题意理解各段函数图象的实际意义,正确理解函数图象横纵坐标表示的意义,理解问题的过程.
【解答】
解:根据图象得:
起跑后1小时内,甲在乙的前面;故正确;
在跑了1小时时,乙追上甲,此时都跑了10千米,故正确;
乙比甲先到达终点,故错误;
设乙跑的直线解析式为:,
将点代入得:,
解析式为:,
当时,,
两人都跑了20千米,故正确.
所以正确.
故选C.
5.【答案】D
【解析】解:由题意知,函数关系为一次函数,由可知,y随x的增大而减小,且当时,,
当时,.
故选:D.
先求出一次函数的关系式,再根据函数图象与坐标轴的交点及函数图象的性质解答即可.
本题考查学生对计算程序及函数性质的理解.根据计算程序可知此计算程序所反映的函数关系为一次函数,然后根据一次函数的图象的性质求解.
6.【答案】C
【解析】
【分析】
本题主要考查一次函数的应用,准确从图像中提取信息是解题关键.
根据图象可知,甲的速度为,乙的速度为,而甲比乙早出发一小时,假设在甲出发t小时候相遇,则有,解方程即可得到结论.
【解答】
解:根据图象可知,
甲的速度为:,乙的速度为:,
设甲出发t小时后两人相遇,则:
,
解得:,
甲出发后两人相遇,
故选C.
7.【答案】C
【解析】
【分析】
此题考查了函数图象的意义解题的关键是根据题意理解各段函数图象的实际意义,正确理解函数图象横纵坐标表示的意义由图象可知起跑后1小时内,甲在乙的前面;在跑了1小时时,乙追上甲,此时都跑了10千米;乙比甲先到达终点;求得乙跑的直线的解析式,即可求得两人跑的距离,则可求得答案.
【解答】
解:根据图象得:
起跑后1小时内,甲在乙的前面;故正确;
在跑了1小时时,乙追上甲,此时都跑了10千米,故正确;
乙比甲先到达终点,故错误;
设乙跑的直线解析式为:,
将点代入得:,
解析式为:,
当时,,
两人都跑了20千米,故正确.
所以三项正确.
故选C.
8.【答案】B
【解析】
【分析】
本题考查了一次函数的应用,解题的关键是仔细观察图象,并从图象中整理出进一步解题的有关信息.由图象可知,不超过100面时,每面收费元,超过100面的部分每面收费元.
【解答】
解:超过100面部分每面收费元,
故选B.
9.【答案】A
【解析】解:由题意可得,
每分钟的进水量为:,
每分钟的出水量为:,
故选:A.
根据题意和函数图象可以求得每分钟的进水量和出水量,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
10.【答案】C
【解析】
【分析】
本题主要考查了函数图象,函数自变量的取值范围,待定系数法求一次函数的解析式,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.服药后3小时,药物浓度直线上升,每小时上升;可知:当时,,当时,y有最大值8,再确定y的取值范围.
【解答】
解:设当时,设,
,
解得:,
;
当时,设,
,
解得:,
,;
当时,,当时,y有最大值8,当时,y的值是,
所以当时,y的取值范围是.
故选C.
11.【答案】C
【解析】
【分析】
本题考查一次函数的应用.
根据图像信息结合一次函数的知识一一解答判断即可.
【解答】
解:由m与t的图像可知当时,千克,
得每天的销售量为,
第10天的销售量为:千克,
故A选项错误;
B.在0至15天,当时,天,
所以在在0至15天期间日销售量不低于24千克的有4天,
在15至20天期间,销售量是逐渐下降的,由图像可知5天降了30千克,每天降低千克,
当,即降低6千克后时,此时t为第16天,
所以试销期间日销售量不低于24千克的有天,
故B选项错误;
C.在天中,设,把分别代入得,,
,
当时,元千克
故C选项正确;
将代入得元千克,
第18天的销售量千克,
试销第18天的销售额为元,
故选项D错误,
故选C.
12.【答案】C
【解析】
【分析】
本题考查一次函数的应用.
根据图像信息结合一次函数的知识一一解答判断即可.
【解答】
解:由m与t的图像可知当时,千克,
得每天的销售量为,
第10天的销售量为:千克,
故A选项错误;
B.在0至15天,当时,天,
所以在在0至15天期间日销售量不低于24千克的有4天,
在15至20天期间,销售量是逐渐下降的,由图像可知5天降了30千克,每天降低千克,
当,即降低6千克后时,此时t为第16天,
所以试销期间日销售量不低于24千克的有天,
故B选项错误;
C.在天中,设,把分别代入得,,
,
当时,元千克
故C选项正确;
将代入得元千克,
第18天的销售量千克,
试销第18天的销售额为元,
故选项D错误,
故选C.
13.【答案】1721
【解析】解:当时,,
则当时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为:,
故答案为:1721.
根据题意,可以求得当时,对应速度y的值,然后根据路程速度时间,即可得到当时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质解答.
14.【答案】
【解析】
【分析】
本题考查了根据实际问题列一次函数关系式,用到的知识点是长方形的周长公式.根据长方形的周长公式列出算式即可.
【解答】
解:一个长方形的长为5cm,宽为?xcm,周长为ycm,则y与x之间的函数表达式为,
故答案为.
15.【答案】1721
【解析】
【分析】
本题考查了函数的关系式和一次函数的应用,找到函数关系式代入数值即可得到对应的函数值,属于比较简单的试题,要求熟练掌握.根据函数关系可以找到对应温度下的传播速度,根据路程时间速度可以得出结论.
【解答】
解:把由题意得声音在空气中传播的速度y与气温x的关系式为:,
当气温时,把代入函数式得.
某人看到闪电5s后才听到声音响,
根据路程时间速度得出:路程,
故答案为1721.
16.【答案】
【解析】
【分析】本题考查了一次函数的应用以及自变量的取值范围,熟记一次函数的性质是解题关键令,求出t即可得解.
【解答】解:表示的是时间,
,
当时,
,
解得:,
.
故答案为.
17.【答案】解:按普通会员会员购买商品应付的金额;
按VIP会员购买商品应付的金额.
当时,;
当时,;
当时,.
答:当时,选择按普通会员购买比较合算;当时,选择两种方式所需费用相同;当时,选择按VIP会员购买比较合算.
【解析】根据两种购买方式的优惠方案,可找出y与x之间的函数关系式;
分,及三种情况,求出x的取值范围或x值,进而可得出结论.
本题考查了一次函数的应用、一元一次不等式的应用以及解一元一次方程,解题的关键是:根据各数量之间的关系,找出y与x之间的函数关系式;分分,及三种情况,分别求出x的取值范围或x的值.
18.【答案】解:设每吨水的政府补贴优惠价为m元,市场调节价为n元.
,解得:,
答:每吨水的政府补贴优惠价2元,市场调节价为元.
当时,,
【解析】设每吨水的政府补贴优惠价为m元,市场调节价为n元,根据题意列出方程组,求解此方程组即可;
根据的结论以及x的范围,即可得出y与x之间的函数关系式.
本题考查了一次函数的应用,题目还考查了二元一次方程组的解法,特别是在求一次函数的解析式时,此函数是一个分段函数,同时应注意自变量的取值范围.
19.【答案】解:根据题意得:,
?化简得,
与x之间的函数关系式为;
?
?
?
?
;
根据题意得:
,
为整数,或9,
,,随x的增大而减小,
,W最小,W最小,?
此时,.
?故选择运口罩9架,运消毒剂4架,运防护服7架,运费最少,最少运费为146400元.
【解析】此题此题考查一次函数的应用,实际问题的方案设计,涉及一次函数的性质,列一次函数解析式,一元一次不等式组的解法.
根据题意和表格中的数据找出等量关系列出关于x和y等式,整理即可得到y与x之间的函数关系式;
根据运费运送各种医疗物资每架飞机运载量飞机数量每吨物资运费列式,然后整理即可求解;
首先根据装运每种医疗物资的飞机都不少于4架,列出关于x的不等式组,并解不等式组求出x的取值范围,然后根据x为整数,确定x的取值,然后根据中得到的函数关系式得到W随x的增大而减小,最后将代入求解即可求出最少运费,再求出运其他两种医疗物资飞机数量即可求解.
20.【答案】解:设每个A型垃圾箱x元,每个B型垃圾箱y元,依题意得
,
解得,
答:每个A型垃圾箱100元,每个B型垃圾箱120元;
由题可得,,
购买A型垃圾箱的数量是B型垃圾箱数量的2倍,
,
解得,
当时,元.
答:购买A型垃圾箱和B型垃圾箱的总费用为3200元.
【解析】依据等量关系列出一元二次方程组,即可得到结论;
依据等量关系列出一次函数解析式,再根据自变量的取值,即可得到函数值.
本题主要考查了一次函数的应用,解决问题的关键是挖掘题目中的关系,找出两个等量关系,列出方程组.
第2页,共2页
第1页,共1页
一、选择题
为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润万元与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是.
A.
4月份的利润为50万元
B.
治污改造完成后每月利润比前一个月增加30万元
C.
治污改造完成前后共有4个月的利润低于100万元
D.
9月份该厂利润达到200万元
A,B两地相距30km,甲乙两人沿同一条路线从A地到B地如图,反映的是两人行进路程与行进时间之间的关系,甲始终是匀速行进,乙的行进不是匀速的;乙用了5个小时到达目的地;乙比甲迟出发小时;甲在出发5小时后被乙追上以上说法正确的个数有
A.
1个
B.
2个
C.
3个
D.
4个
随着“互联网”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用单位:元与行驶里程单位:千米的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为?
A.
33元
B.
36元
C.
40元
D.
42元
在盐城全民健身越野赛中,甲、乙两选手的行程千米随时间时变化的图象全程如图所示.下列四种说法:起跑后1小时内,甲在乙的前面;第1小时两人都跑了10千米;
甲比乙先到达终点;???????????????两人都跑了20千米.
正确的有
A.
B.
C.
D.
如图所示的计算程序中,y与x之间的函数关系所对应的图象应为
A.
B.
C.
D.
已知A、B两地相距12km,甲、乙两人沿同一条公路分别从A,B两地出发相向而行,甲、乙两人离B地的路程与时间的函数关系图象如图所示,则两人在甲出发后相遇所需的时间是
A.
B.
C.
D.
在无锡全民健身越野赛中,甲、乙两选手的行程千米随时间时变化的图象全程如图所示.下列四种说法:起跑后1小时内,甲在乙的前面;第1小时两人都跑了10千米;甲比乙先到达终点;两人都跑了20千米.正确的有
A.
B.
C.
D.
复印店复印收费元与复印面数面的函数图象如图所示,从图象中可以看出,复印超过100面的部分,每面收费
A.
元
B.
元
C.
元
D.
元
一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量与时间之间的关系如图所示,则每分钟的进水量与出水量分别是
A.
5
L,
B.
,5
L
C.
5
L,
D.
,5
L
药品研究所开发一种抗菌新药,经多年动物实验之后,首次用于临床人体试验,测得成人服药后血液中药物浓度微克毫升与服药后时间时之间的函数关系如图所示,则当时,y的取值范围是
A.
B.
C.
D.
某超市从元旦起,在20天内试销一种特种水果.试销期间的日销售量千克与销售时间天,销售单价元千克与销售时间天之间的函数图象如图所示.那么,下列说法正确的是?
?
?
?
A.
试销第10天的销售量为15千克
B.
试销期间日销售量不低于24千克的有4天
C.
试销第16天的销售单价为元千克
D.
试销第18天的销售额为100元
某超市从元旦起,在20天内试销一种特种水果.试销期间的日销售量千克与销售时间天,销售单价元千克与销售时间天之间的函数图象如图所示.那么,下列说法正确的是
A.
试销第10天的销售量为15千克
B.
试销期间日销售量不低于24千克的有4天
C.
试销第16天的销售单价为元千克
D.
试销第18天的销售额为100元
二、填空题
空气中传播的速度与气温之间的关系式为;当时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为______
已知一个长方形的长为5cm,宽为xcm,周长为ycm,则y与x之间的函数表达式为________.
声音在空气中传播的速度与气温之间在如下关系:当气温时,某人看到闪电5s后才听到声音光传播的时间忽略不计则此人与发生闪电所在地相距__________m.
小明正在参加学校运动会的百米赛跑,他距终点的路程米与他起跑时间秒之间的函数关系式为:,则自变量t的取值范围是________.
三、解答题
随着网络电商与快递行业的飞速发展,叠加疫情影响,越来越多的人选择网络购物.在暑期来临之际,天猫超市为了促销,推出了普通会员与VIP会员两种销售方式,普通会员的收费方式是:所购商品的金额不超过300元,客户还需支付快递费20元;如果所购商品的金额超过300元,则所购商品给予8折优惠,并免除20元的快递费,VIP会员的收费方式是:缴纳VIP会员费50元,所购商品给予折优惠,并免除20元的快递费.
请分别写出按普通会员、VIP会员购买商品应付的金额元与所购商品的金额元之间的函数关系式;
某网民计划在促销活动期间在天猫超市购买元的商品,则他应该选择哪种购买方式比较合算?
某市为了鼓励居民节约用水,决定实行两级收费制度.每月用水量不超过14吨含14吨的,按政府补贴优惠价m元吨收费;若每月用水量超过14吨,则超过部分按市场价n元吨收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
求每吨水的政府补贴优惠价和市场价分别是多少?
设每月用水量为吨,应交水费为y元,请写出y与x之间的函数关系式.
2020年新冠肺炎疫情在全球蔓延,全球疫情大考面前,中国始终同各国安危与共、风雨同舟,时至5月,中国已经向150多个国家和国际组织提供医疗物资援助.某次援助,我国组织20架飞机装运口罩、消毒剂、防护服三种医疗物资共120吨,按计划20架飞机都要装运,每架飞机只能装运同一种医疗物资,且必须装满.根据如下表提供的信息,解答以下问题:
防疫物资种类
口罩
消毒剂
防护服
每架飞机运载量吨
8
5
4
每吨物资运费元
1200
1600
1000
若有x架飞机装运口罩,有y架飞机装运消毒剂,求y与x之间的函数关系式;
若此次物资运费为W元,求W与x之间的函数关系式;
如果装运每种医疗物资的飞机都不少于4架,那么怎样安排运送物资,才能使此次物资运费最少,最少运费为多少元?
为迎接“国家卫生城市”复检,某市环卫局准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
每个A型垃圾箱和B型垃圾箱各多少元?
现需要购买A,B两种型号的垃圾箱共30个,设购买A型垃圾箱a个,购买A型垃圾箱和B型垃圾箱的总费用为w元,求w与a的函数表达式.如果购买A型垃圾箱的数量是B型垃圾箱数量的2倍,求购买A型垃圾箱和B型垃圾箱的总费用.
答案和解析
1.【答案】C
【解析】
【分析】
此题主要考查了一次函数与反比例函数的应用,正确得出函数解析式是解题关键.
直接利用已知点求出一次函数与反比例函数的解析式进而分别分析得出答案.
【解答】
解:设反比例函数的解析式为,
把代入得,,
反比例函数的解析式为:,
当时,,
月份的利润为50万元,故此选项正确,不合题意;
B.治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C.当时,则,
解得:,
设一次函数解析式为:,
则,
解得:,
故一次函数解析式为:,
当时,则,
则只有3月,4月,5月,共3个月的利润低于100万元,故此选项不正确,符合题意.
D.一次函数解析式为:,
故时,,
解得:,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选C.
2.【答案】B
【解析】解:由图象可得,
甲始终是匀速行进,乙的行进不是匀速的,故正确;
乙用了个小时到达目的地,故错误;
乙比甲迟出发小时,故正确;
甲在出发不到5小时后被乙追上,故错误;
故选:B.
根据题意和函数图象中的数据,可以判断各个小题中的结论是否正确,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
3.【答案】C
【解析】
【分析】
本题主要考查一次函数的图象与待定系数法求一次函数解析式,熟练掌握待定系数法求得一次函数解析式是解题的关键.
待定系数法求出时y关于x的函数解析式,再求出时y的值即可.
【解答】
解:当行驶里程时,设,
将、代入,得:,
解得:,
,
?当时,,
?如果小明某次打车行驶里程为22千米,则他的打车费用为40元.
故选C.
4.【答案】C
【解析】
【分析】
由图象可知起跑后1小时内,甲在乙的前面;在跑了1小时时,乙追上甲,此时都跑了10千米;乙比甲先到达终点;求得乙跑的直线的解析式,即可求得两人跑的距离,则可求得答案.此题考查了函数图形的意义解题的关键是根据题意理解各段函数图象的实际意义,正确理解函数图象横纵坐标表示的意义,理解问题的过程.
【解答】
解:根据图象得:
起跑后1小时内,甲在乙的前面;故正确;
在跑了1小时时,乙追上甲,此时都跑了10千米,故正确;
乙比甲先到达终点,故错误;
设乙跑的直线解析式为:,
将点代入得:,
解析式为:,
当时,,
两人都跑了20千米,故正确.
所以正确.
故选C.
5.【答案】D
【解析】解:由题意知,函数关系为一次函数,由可知,y随x的增大而减小,且当时,,
当时,.
故选:D.
先求出一次函数的关系式,再根据函数图象与坐标轴的交点及函数图象的性质解答即可.
本题考查学生对计算程序及函数性质的理解.根据计算程序可知此计算程序所反映的函数关系为一次函数,然后根据一次函数的图象的性质求解.
6.【答案】C
【解析】
【分析】
本题主要考查一次函数的应用,准确从图像中提取信息是解题关键.
根据图象可知,甲的速度为,乙的速度为,而甲比乙早出发一小时,假设在甲出发t小时候相遇,则有,解方程即可得到结论.
【解答】
解:根据图象可知,
甲的速度为:,乙的速度为:,
设甲出发t小时后两人相遇,则:
,
解得:,
甲出发后两人相遇,
故选C.
7.【答案】C
【解析】
【分析】
此题考查了函数图象的意义解题的关键是根据题意理解各段函数图象的实际意义,正确理解函数图象横纵坐标表示的意义由图象可知起跑后1小时内,甲在乙的前面;在跑了1小时时,乙追上甲,此时都跑了10千米;乙比甲先到达终点;求得乙跑的直线的解析式,即可求得两人跑的距离,则可求得答案.
【解答】
解:根据图象得:
起跑后1小时内,甲在乙的前面;故正确;
在跑了1小时时,乙追上甲,此时都跑了10千米,故正确;
乙比甲先到达终点,故错误;
设乙跑的直线解析式为:,
将点代入得:,
解析式为:,
当时,,
两人都跑了20千米,故正确.
所以三项正确.
故选C.
8.【答案】B
【解析】
【分析】
本题考查了一次函数的应用,解题的关键是仔细观察图象,并从图象中整理出进一步解题的有关信息.由图象可知,不超过100面时,每面收费元,超过100面的部分每面收费元.
【解答】
解:超过100面部分每面收费元,
故选B.
9.【答案】A
【解析】解:由题意可得,
每分钟的进水量为:,
每分钟的出水量为:,
故选:A.
根据题意和函数图象可以求得每分钟的进水量和出水量,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
10.【答案】C
【解析】
【分析】
本题主要考查了函数图象,函数自变量的取值范围,待定系数法求一次函数的解析式,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.服药后3小时,药物浓度直线上升,每小时上升;可知:当时,,当时,y有最大值8,再确定y的取值范围.
【解答】
解:设当时,设,
,
解得:,
;
当时,设,
,
解得:,
,;
当时,,当时,y有最大值8,当时,y的值是,
所以当时,y的取值范围是.
故选C.
11.【答案】C
【解析】
【分析】
本题考查一次函数的应用.
根据图像信息结合一次函数的知识一一解答判断即可.
【解答】
解:由m与t的图像可知当时,千克,
得每天的销售量为,
第10天的销售量为:千克,
故A选项错误;
B.在0至15天,当时,天,
所以在在0至15天期间日销售量不低于24千克的有4天,
在15至20天期间,销售量是逐渐下降的,由图像可知5天降了30千克,每天降低千克,
当,即降低6千克后时,此时t为第16天,
所以试销期间日销售量不低于24千克的有天,
故B选项错误;
C.在天中,设,把分别代入得,,
,
当时,元千克
故C选项正确;
将代入得元千克,
第18天的销售量千克,
试销第18天的销售额为元,
故选项D错误,
故选C.
12.【答案】C
【解析】
【分析】
本题考查一次函数的应用.
根据图像信息结合一次函数的知识一一解答判断即可.
【解答】
解:由m与t的图像可知当时,千克,
得每天的销售量为,
第10天的销售量为:千克,
故A选项错误;
B.在0至15天,当时,天,
所以在在0至15天期间日销售量不低于24千克的有4天,
在15至20天期间,销售量是逐渐下降的,由图像可知5天降了30千克,每天降低千克,
当,即降低6千克后时,此时t为第16天,
所以试销期间日销售量不低于24千克的有天,
故B选项错误;
C.在天中,设,把分别代入得,,
,
当时,元千克
故C选项正确;
将代入得元千克,
第18天的销售量千克,
试销第18天的销售额为元,
故选项D错误,
故选C.
13.【答案】1721
【解析】解:当时,,
则当时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为:,
故答案为:1721.
根据题意,可以求得当时,对应速度y的值,然后根据路程速度时间,即可得到当时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质解答.
14.【答案】
【解析】
【分析】
本题考查了根据实际问题列一次函数关系式,用到的知识点是长方形的周长公式.根据长方形的周长公式列出算式即可.
【解答】
解:一个长方形的长为5cm,宽为?xcm,周长为ycm,则y与x之间的函数表达式为,
故答案为.
15.【答案】1721
【解析】
【分析】
本题考查了函数的关系式和一次函数的应用,找到函数关系式代入数值即可得到对应的函数值,属于比较简单的试题,要求熟练掌握.根据函数关系可以找到对应温度下的传播速度,根据路程时间速度可以得出结论.
【解答】
解:把由题意得声音在空气中传播的速度y与气温x的关系式为:,
当气温时,把代入函数式得.
某人看到闪电5s后才听到声音响,
根据路程时间速度得出:路程,
故答案为1721.
16.【答案】
【解析】
【分析】本题考查了一次函数的应用以及自变量的取值范围,熟记一次函数的性质是解题关键令,求出t即可得解.
【解答】解:表示的是时间,
,
当时,
,
解得:,
.
故答案为.
17.【答案】解:按普通会员会员购买商品应付的金额;
按VIP会员购买商品应付的金额.
当时,;
当时,;
当时,.
答:当时,选择按普通会员购买比较合算;当时,选择两种方式所需费用相同;当时,选择按VIP会员购买比较合算.
【解析】根据两种购买方式的优惠方案,可找出y与x之间的函数关系式;
分,及三种情况,求出x的取值范围或x值,进而可得出结论.
本题考查了一次函数的应用、一元一次不等式的应用以及解一元一次方程,解题的关键是:根据各数量之间的关系,找出y与x之间的函数关系式;分分,及三种情况,分别求出x的取值范围或x的值.
18.【答案】解:设每吨水的政府补贴优惠价为m元,市场调节价为n元.
,解得:,
答:每吨水的政府补贴优惠价2元,市场调节价为元.
当时,,
【解析】设每吨水的政府补贴优惠价为m元,市场调节价为n元,根据题意列出方程组,求解此方程组即可;
根据的结论以及x的范围,即可得出y与x之间的函数关系式.
本题考查了一次函数的应用,题目还考查了二元一次方程组的解法,特别是在求一次函数的解析式时,此函数是一个分段函数,同时应注意自变量的取值范围.
19.【答案】解:根据题意得:,
?化简得,
与x之间的函数关系式为;
?
?
?
?
;
根据题意得:
,
为整数,或9,
,,随x的增大而减小,
,W最小,W最小,?
此时,.
?故选择运口罩9架,运消毒剂4架,运防护服7架,运费最少,最少运费为146400元.
【解析】此题此题考查一次函数的应用,实际问题的方案设计,涉及一次函数的性质,列一次函数解析式,一元一次不等式组的解法.
根据题意和表格中的数据找出等量关系列出关于x和y等式,整理即可得到y与x之间的函数关系式;
根据运费运送各种医疗物资每架飞机运载量飞机数量每吨物资运费列式,然后整理即可求解;
首先根据装运每种医疗物资的飞机都不少于4架,列出关于x的不等式组,并解不等式组求出x的取值范围,然后根据x为整数,确定x的取值,然后根据中得到的函数关系式得到W随x的增大而减小,最后将代入求解即可求出最少运费,再求出运其他两种医疗物资飞机数量即可求解.
20.【答案】解:设每个A型垃圾箱x元,每个B型垃圾箱y元,依题意得
,
解得,
答:每个A型垃圾箱100元,每个B型垃圾箱120元;
由题可得,,
购买A型垃圾箱的数量是B型垃圾箱数量的2倍,
,
解得,
当时,元.
答:购买A型垃圾箱和B型垃圾箱的总费用为3200元.
【解析】依据等量关系列出一元二次方程组,即可得到结论;
依据等量关系列出一次函数解析式,再根据自变量的取值,即可得到函数值.
本题主要考查了一次函数的应用,解决问题的关键是挖掘题目中的关系,找出两个等量关系,列出方程组.
第2页,共2页
第1页,共1页
