7.4 二元一次方程与一次函数 同步练习(含答案)
文档属性
| 名称 | 7.4 二元一次方程与一次函数 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章 二元一次方程组
4 二元一次方程与一次函数
知识能力全练
知识点一 二元一次方程与一次函数的关系
1.如图所示的平面直角坐标系内有四条直线1、2、3、4,则方程3x-5y+15=0表示的直线是( )
A.1 B.2 C.3 D.4
2.以方程4x+y=12的解为坐标的点组成的图象是一条直线,则这条直线对应的一次函数表达式为( )
A.y=4x+12 B.y=4x-12 C.y=-4x+12 D.y=-4x-12
3.某一次函数的图象如图2所示,则与其相对应的二元一次方程为( )
A.x-3y=3 B.x+3y=3 C.3x-y=1 D.3x+y=1
知识点二 二元一次方程组与一次函数的关系
4.如图所示,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组的解,那么这个点是( )
A.M B.N C.E D.F
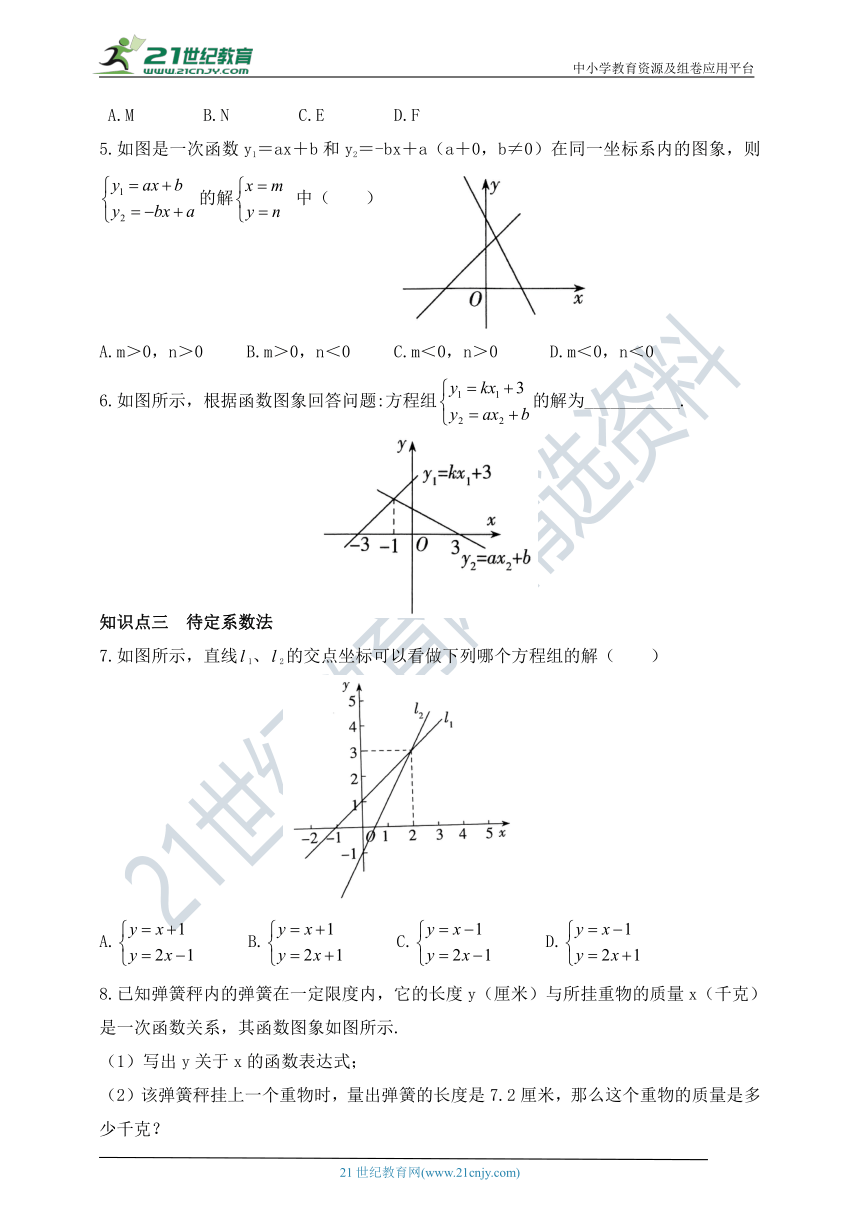
5.如图是一次函数y1=ax+b和y2=-bx+a(a+0,b≠0)在同一坐标系内的图象,则的解 中( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
6.如图所示,根据函数图象回答问题:方程组的解为___________.
知识点三 待定系数法
7.如图所示,直线1、2的交点坐标可以看做下列哪个方程组的解( )
A. B. C. D.
8.已知弹簧秤内的弹簧在一定限度内,它的长度y(厘米)与所挂重物的质量x(千克)是一次函数关系,其函数图象如图所示.
(1)写出y关于x的函数表达式;
(2)该弹簧秤挂上一个重物时,量出弹簧的长度是7.2厘米,那么这个重物的质量是多少千克?
9.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.请你根据图象进行探究:
(1)小王和小李的速度分别是多少?
(2)求线段BC所表示的y与x之间的函数表达式,并写出自变量x的取值范围.
10.函数y=-x+4与y=x+2的图象如图所示,则方程组的解为( )
A. B. C. D.
11.如图所示,一次函数y=kx+b的图象1与一次函数y=-x+3的图象2相交于点P,则方程组,的解为_____________.
12.如图所示,直线1的函数表达式为y=3x-2,且直线1与x轴交于点D.直线2与x轴交于点A,且经过点B(4,1),直线1与2交于点C(m,3).
(1)求点D和点C的坐标;
(2)求直线2的函数表达式;
(3)利用函数图象写出关于x,y的二元一次方程组的解.
13.数形结合是解决数学问题常用的思想方法.如图所示,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
14.若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-x+b-1上,则常数b=( )
A. B.2 C.-1 D.1
15.已知二元一次方程组的解为.则在同一平面直角坐标系中,直线1:y=x+5与直线2:y=-x-1的交点坐标为__________.
16.为让更多的学生学会游泳,少年宫新建了一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变,同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度.
17利用图象法解方程组
18.如图所示,已知直线1:y=3x+1与y轴交于点A,且和直线2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
(1)求a的值,判断直线3:y=-nx-2m是否也经过点P,请说明理由;
(2)请直接写出关于x,y的方程组的解;
(3)若直线1,2表示的两个一次函数都大于O,此时恰好x>3,求直线2的函数解析式.
参考答案
1.A 2.C 3.A 4.C 5.A
6.答案
解析 根据题图知直线y1=kx1+3经过点(-3,0),所以-3k+3=0,解得k=1,
所以y1=x1+3,当x1=-1时,y1=2,所以两个函数图象的交点坐标为(-1,2),
所以方程组的解为.
7.A
8.解析 (1)设y关于x的函数表达式为y=kx+b(k≠0),
由题意得,解得{,∴y关于x的函数表达式为y=x+6.
(2)当y=7.2时,x+6=7.2,解得x=2.
答:这个重物的质量是2千克.
9.解析 (1)由题图可得,小王的速度为30÷3=10km/h,
小李的速度为(30-10×1)÷1=20km/h.
答:小王和小李的速度分别是10km/h和20km/h.
(2)小李从乙地到甲地用的时间为30÷20=1.5h,
当小李到达甲地时,两人之间的距离为10×1.5=15km,
∴点C的坐标为(1.5,15),
设线段BC所表示的y与x之间的函数表达式为y=kx+b(k≠0),
把B、C的坐标代入,得解得,
即线段BC所表示的y与x之间的函数表达式是y=30x-30(1≤x≤1.5)
10.B
11.答案
解析 从题图可知,两函数图象都经过点P(a,2),
把点P的坐标代入一次函数y=-x+3,得2=-a+3解得a=1,
即点P的坐标为(1,2),所以方程组的解为
12.解析 (1)在y=3x-2中,令y=0,即3x-2=0,解得x=,
∴点D的坐标为(,0).∵点C(m,3)在直线y=3x-2上,
∴3m-2=3,∴m=,∴点C的坐标为(,3).
(2)设直线2的函数表达式为y=kx+b(k≠0),
由题意,得,解得,∴直线2的函数表达式为.
(3)∵直线1与2交于点C,∴点C的坐标即为方程组的解,
∴二元一次方程组的解为=.
13.A 14.B
15.答案 (-4,1)
解析 二元一次方程组的解为,
∴直线1:y=x+5与直线2:y=-x-1的交点坐标为(-4,1).
16.解析 设一次函数的关系式为y=kx+b(k≠0),根据图象过点(0,100),(2,380),得,解得,
∴游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式为y=140x+100.
同时打开甲、乙两个进水口的注水速度为(m3/h).
17.解析 在同一平面直角坐标系中画出一次函数y=-x+4与一次函数y=2x+1的图象,得
直线y=-x+4与直线y=2x+1的交点坐标为(1,3),
所以二元一次方程组的解为.
18.解析 (1)∵(-2,a)在直线y=3x+1上,∴a=3(-2)+1=-5.
直线3:y=-nx-2m也经过点P.
理由:∵点P(-2,-5)在直线y=mx+n上,∴-2m+n=-5,
∴将P点的横坐标-2代入y=-nx-2m,得y=-n×(-2)-2m=-2m+n=-5,这说明直线3也经过点P.
(2)方程组,的解为
(3)∵直线1,2表示的两个一次函数都大于0,此时恰好x>3,
∴直线2经过点(3,0),又∵直线2经过点P(-2,-5),
∴,解得,
∴直线2的函数解析式为y=x-3.
_21?????????è?????(www.21cnjy.com)_
第七章 二元一次方程组
4 二元一次方程与一次函数
知识能力全练
知识点一 二元一次方程与一次函数的关系
1.如图所示的平面直角坐标系内有四条直线1、2、3、4,则方程3x-5y+15=0表示的直线是( )
A.1 B.2 C.3 D.4
2.以方程4x+y=12的解为坐标的点组成的图象是一条直线,则这条直线对应的一次函数表达式为( )
A.y=4x+12 B.y=4x-12 C.y=-4x+12 D.y=-4x-12
3.某一次函数的图象如图2所示,则与其相对应的二元一次方程为( )
A.x-3y=3 B.x+3y=3 C.3x-y=1 D.3x+y=1
知识点二 二元一次方程组与一次函数的关系
4.如图所示,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x、y的二元一次方程组的解,那么这个点是( )
A.M B.N C.E D.F
5.如图是一次函数y1=ax+b和y2=-bx+a(a+0,b≠0)在同一坐标系内的图象,则的解 中( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
6.如图所示,根据函数图象回答问题:方程组的解为___________.
知识点三 待定系数法
7.如图所示,直线1、2的交点坐标可以看做下列哪个方程组的解( )
A. B. C. D.
8.已知弹簧秤内的弹簧在一定限度内,它的长度y(厘米)与所挂重物的质量x(千克)是一次函数关系,其函数图象如图所示.
(1)写出y关于x的函数表达式;
(2)该弹簧秤挂上一个重物时,量出弹簧的长度是7.2厘米,那么这个重物的质量是多少千克?
9.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.请你根据图象进行探究:
(1)小王和小李的速度分别是多少?
(2)求线段BC所表示的y与x之间的函数表达式,并写出自变量x的取值范围.
10.函数y=-x+4与y=x+2的图象如图所示,则方程组的解为( )
A. B. C. D.
11.如图所示,一次函数y=kx+b的图象1与一次函数y=-x+3的图象2相交于点P,则方程组,的解为_____________.
12.如图所示,直线1的函数表达式为y=3x-2,且直线1与x轴交于点D.直线2与x轴交于点A,且经过点B(4,1),直线1与2交于点C(m,3).
(1)求点D和点C的坐标;
(2)求直线2的函数表达式;
(3)利用函数图象写出关于x,y的二元一次方程组的解.
13.数形结合是解决数学问题常用的思想方法.如图所示,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
14.若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-x+b-1上,则常数b=( )
A. B.2 C.-1 D.1
15.已知二元一次方程组的解为.则在同一平面直角坐标系中,直线1:y=x+5与直线2:y=-x-1的交点坐标为__________.
16.为让更多的学生学会游泳,少年宫新建了一个游泳池,其容积为480m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自的注水速度保持不变,同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度.
17利用图象法解方程组
18.如图所示,已知直线1:y=3x+1与y轴交于点A,且和直线2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
(1)求a的值,判断直线3:y=-nx-2m是否也经过点P,请说明理由;
(2)请直接写出关于x,y的方程组的解;
(3)若直线1,2表示的两个一次函数都大于O,此时恰好x>3,求直线2的函数解析式.
参考答案
1.A 2.C 3.A 4.C 5.A
6.答案
解析 根据题图知直线y1=kx1+3经过点(-3,0),所以-3k+3=0,解得k=1,
所以y1=x1+3,当x1=-1时,y1=2,所以两个函数图象的交点坐标为(-1,2),
所以方程组的解为.
7.A
8.解析 (1)设y关于x的函数表达式为y=kx+b(k≠0),
由题意得,解得{,∴y关于x的函数表达式为y=x+6.
(2)当y=7.2时,x+6=7.2,解得x=2.
答:这个重物的质量是2千克.
9.解析 (1)由题图可得,小王的速度为30÷3=10km/h,
小李的速度为(30-10×1)÷1=20km/h.
答:小王和小李的速度分别是10km/h和20km/h.
(2)小李从乙地到甲地用的时间为30÷20=1.5h,
当小李到达甲地时,两人之间的距离为10×1.5=15km,
∴点C的坐标为(1.5,15),
设线段BC所表示的y与x之间的函数表达式为y=kx+b(k≠0),
把B、C的坐标代入,得解得,
即线段BC所表示的y与x之间的函数表达式是y=30x-30(1≤x≤1.5)
10.B
11.答案
解析 从题图可知,两函数图象都经过点P(a,2),
把点P的坐标代入一次函数y=-x+3,得2=-a+3解得a=1,
即点P的坐标为(1,2),所以方程组的解为
12.解析 (1)在y=3x-2中,令y=0,即3x-2=0,解得x=,
∴点D的坐标为(,0).∵点C(m,3)在直线y=3x-2上,
∴3m-2=3,∴m=,∴点C的坐标为(,3).
(2)设直线2的函数表达式为y=kx+b(k≠0),
由题意,得,解得,∴直线2的函数表达式为.
(3)∵直线1与2交于点C,∴点C的坐标即为方程组的解,
∴二元一次方程组的解为=.
13.A 14.B
15.答案 (-4,1)
解析 二元一次方程组的解为,
∴直线1:y=x+5与直线2:y=-x-1的交点坐标为(-4,1).
16.解析 设一次函数的关系式为y=kx+b(k≠0),根据图象过点(0,100),(2,380),得,解得,
∴游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式为y=140x+100.
同时打开甲、乙两个进水口的注水速度为(m3/h).
17.解析 在同一平面直角坐标系中画出一次函数y=-x+4与一次函数y=2x+1的图象,得
直线y=-x+4与直线y=2x+1的交点坐标为(1,3),
所以二元一次方程组的解为.
18.解析 (1)∵(-2,a)在直线y=3x+1上,∴a=3(-2)+1=-5.
直线3:y=-nx-2m也经过点P.
理由:∵点P(-2,-5)在直线y=mx+n上,∴-2m+n=-5,
∴将P点的横坐标-2代入y=-nx-2m,得y=-n×(-2)-2m=-2m+n=-5,这说明直线3也经过点P.
(2)方程组,的解为
(3)∵直线1,2表示的两个一次函数都大于0,此时恰好x>3,
∴直线2经过点(3,0),又∵直线2经过点P(-2,-5),
∴,解得,
∴直线2的函数解析式为y=x-3.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
