物理北师大版八年级下册 第9章 五、探究——使用机械是否省功 习题(word版带解析)
文档属性
| 名称 | 物理北师大版八年级下册 第9章 五、探究——使用机械是否省功 习题(word版带解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 146.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览



文档简介
第9章 五、探究——使用机械是否省功
一、单选题
1.???下列关于功、功率、机械效率的说法中正确的是( )
A.?机械效率越高,机械做功一定越快????????????????????????????????????????
B.?越省力的机械,其机械效率一定越高????????????????????????????????????????
C.?做功越慢的机械,功率一定越小????????????????????????????????????????
D.?功率不同的机器,做的功一定不相等
2.???下列关于功率和机械效率说法中正确的是( )
A.?做功多的物体,功率一定大????????????????????????????????????????
B.?做功快的物体,功率一定大????????????????????????????????????????
C.?有用功越大,机械的效率就越高????????????????????????????????????????
D.?额外功越大,机械的效率就越低
3.???关于功率和机械效率,下列说法正确的是( )
A.?功率大的机械,做功一定快????????????????????????????????????????
B.?功率大的机械,机械效率一定高????????????????????????????????????????
C.?做的有用功多,机械效率一定高????????????????????????????????????????
D.?省力的机械,机械效率一定高
4.???某起重机把货物匀速提升到三楼,用时为t1;起重机经保养后,提高了机械效率,当匀速提升同样货物到相同的高度,用时为t2,与第一次提升相比,第二次( )
A.?t2<t1?????????????????????????
B.?有用功较多?????????????????????????
C.?额外功较少?????????????????????????
D.?总功较多
5.???如图所示,质量分布均匀的杠杆在中点处悬挂一重力为24N的物体,用大小为16N的拉力F竖直向上匀速拉动杆,使物体在5s内缓慢升高10cm。若不计一切摩擦及阻力,下列说法错误的是( )
A.?这是一个省力杠杆????????????????????????????????????????
B.?整个过程中,所做的有用功为2.4J????????????????????????????????????????
C.?整个过程中,所做的额外功为0.8J????????????????????????????????????????
D.?整个过程中,拉力F的作用点上升的距离为5cm
6.???关于功、功率、机械效率,下列说法中正确的是( )
A.?物体受力且运动时,力对物体就做了功????????????????????????????????????????
B.?功率大的机器做功就快????????????????????????????????????????
C.?做功快的机器其机械效率一定高????????????????????????????????????????
D.?功率小的机器做功一定少
7.???甲吊车比乙吊车的机械效率高,当它们分别把相同质量的物体匀速提升相同高度时,则( )
A.?甲吊车的电动机做的有用功较多????????????????????????????????????????
B.?甲吊车的电动机做的总功较多????????????????????????????????????????
C.?乙吊车的电动机做的额外功较多????????????????????????????????????????
D.?甲、乙两吊车的电动机做的总功相同
8.???下面说法正确的是( )
A.?功率越大的机械,机械效率越高????????????????????????????????????????
B.?减少了总功,就能提高机械效率????????????????????????????????????????
C.?额外功在总功中所占比例越小,机械效率一定越高????????????????????????????????????????
D.?省力越多的机械,机械效率一定越高
9.???要提高某机械的机械效率,应该( )
A.?减小外力所移动的距离?????????????????????????
B.?减小动滑轮的质量?????????????????????????
C.?减小总功?????????????????????????
D.?减小外力
10.???下列关于功、功率、机械效率的说法正确的是( )
A.?额外功与总功之比越小,机械效率一定越大????????????????????????????????????????
B.?机器的功率越小,机械效率一定越低????????????????????????????????????????
C.?功率不同的机器,做的功一定不相等????????????????????????????????????????
D.?物体做功越多,功率一定越大
二、填空题
1.???如图所示,斜面长1m,高0.4m,用大小为5N沿斜面向上的拉力F,经2秒钟将重10N的铁块从底端匀速拉到顶端,在该过程中,有用功为______J;拉力做功的功率为______;斜面的机械效率为______%
???如图所示,工人用平行于斜面的推力,把一个重为1000N的物体,沿着长5m、高1m的斜面由底端匀速推到顶端,推力的大小为300N,则推力所做的有用功为______J,物体与斜面的摩擦力为______N。
???在日常生活和工农业生产中,提高机械效率有着重要的意义。小亮利用如图装置测斜面的机械效率。斜面的机械效率与斜面的倾斜程度和摩擦有关,与物重无关。
(1)保持斜面倾斜程度不变,可以采用______的方法减小摩擦,从而提高斜面的机械效率。
(2)实验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都______。
???如图所示,将一个重3N的物体匀速拉到斜面顶端,人沿斜面向上的拉力为2N,物体沿斜面移动的距离为0.8m,上升的高度为0.4m,则物体重力做功为______J,分析数据可知利用斜面______(能/不能)省功,斜面的机械效率是______。
5.???如图,斜面长10m、高2m,工人用沿斜面向上25N的力,用了2s把重100N的箱子匀速推到车上,则推力的功率是______W;该斜面机械效率是______%。箱子受到斜面摩擦力是______N.
三、实验探究题
1.???学习了机械效率知识后,全班同学对“斜面的机械效率跟什么因素有关”这一课题提出了一些值得探究的猜想:A、斜面的机械效率跟斜面的倾斜程度有关;B、跟斜面的粗糙程度有关;C、跟斜面的长度有关;D、跟物体的重力有关。小明同学为了证实其中的部分猜想是否正确,设计方案并进行了探究,他的探究实验数据如下表。
实验次数
斜面倾角
斜面粗糙程度
物重
G/N
斜面高度
h/m
沿斜面拉力
F/N
斜面长
s/m
有用功
W有/J
总功
W总/J
机械效率
η(%)
①
30°
粗糙
1
0.5
0.7
1
0.5
0.7
②
30°
稍光滑
1
0.5
0.6
1
0.5
83.3
③
45°
粗糙同①
1
0.7
0.9
1
0.9
77.8
(1)请你替小明在上表中的空格处填上适当的数据W有______、W总______、η=______(保留一位小数)
(2)通过对比实验①②数据,可验证猜想______(填写字母)。
(3)通过对比实验①③数据,可以得出的探究结论是:______。
(4)若要验证猜想D,应控制斜面的长、斜面的______和______不改变。
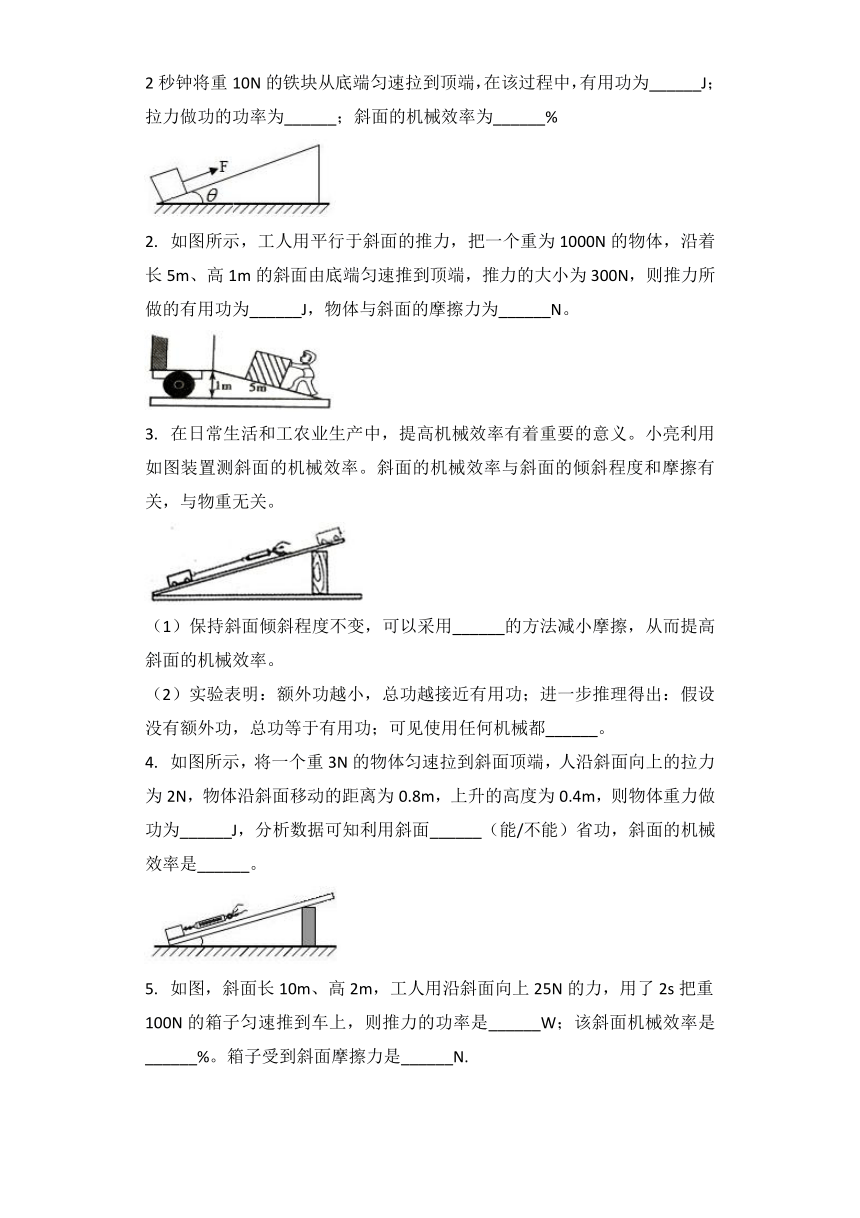
2.???在探究“杠杆平衡条件”实验中(每个钩码质量相等,杠杆上每小格等距):
?(1)将杠杆的中点O挂在支架上后,调节杠杆两端螺母使杠杆在水平位置平衡,目的是______;
(2)杠杆平衡后,小明同学在图甲所示的A位置挂上两个钩码,可在B位置挂上______个钩码,使杠杆在水平位置平衡;
(3)取下B位置的钩码,改用弹簧测力计拉杠杆的C点使杠杆在水平位置保持平衡。当弹簧测力计由位置1转至位置2的过程中,杠杆在水平位置始终保持平衡(如图乙),测力计示数将______(选填“一直变大”、“一直变小”、“先变大后变小”、“先变小后变大”);
(4)接着小明把支点选到B点,如图丙,在A点挂一个钩码,在C点挂3个钩码,杠杆也恰好水平静止,她觉得此时不满足杠杆平衡条件,造成这个问题的原因是______;
(5)完成以上实验后,小明利用杠杆来测量测量杠杆的机械效率。如图丁,实验时,竖直向上拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。实验中,将杠杆拉至图中虚线位置测力计的示数F=______N,钩码总重G为1.0N,钩码上升高度h为0.1m,测力计移动距离s为0.3m,则杠杆的机械效率为______%(结果精确到0.1%)。如果把钩码由A移至B,两次实验A点竖直移动相同距离,拉力所做的有用功将______,此杠杆的机械效率将______(两空均选填“变大”、“变小”或“不变”)。
四、简答题
1.???功的原理告诉我们:使用机械可以省力,不能省功。我们登山时,常常爱走小路,不喜欢走大路,盘山的大路都是斜面,难道不省力吗?
2.???如图所示,两小儿之辩,关于机械省力,省功以及机械效率的辩论,你支持哪一方的说法?不支持另外一方的原因是什么?
五、计算题
1.???工人师傅要将重为1200N的木箱搬到1m高的车厢里.他将一块6m长的木板搁在地面与车厢之间构成斜面,然后站在车上用300N的拉力将物体从斜面底端匀速拉到车厢里,如图所示,求:
(1)工人所做的有用功。
(2)物体所受斜面的摩擦力。
第9章 五、探究——使用机械是否省功
【答案】
1.??C???????2.??B???????3.??A???????4.??C???????5.??D???????
6.??B???????7.??C???????8.??C???????9.??B???????10.??A???????
【解析】
1.??
解:A、机械效率是指有用功与总功的比值,功率反应物体做功的快慢,机械效率与机械功率大小没有直接关系,故A错误;
B、机械效率是有用功与总功的比值,与机械的省力情况无关,故B错误;
C、功率反映做功的快慢,功率大则做功快,功率小说明做功慢,故C正确;
D、功率不同的机械,做的功有可能相等。如功率为5000W的机械60s做的功与功率为1000W的机械300s做的功相同,故D错误。
故选:C。
①功率是描述物体做功快慢的物理量,它等于单位时间内所做的功,功率大则做功快;
②机械效率反映了机械的性能优劣,是有用功与总功的比值;
③机械效率与机械做功功率和机械的省力情况无关。
深刻理解功率和机械效率的概念是解决此题的关键,要充分考虑选项中的条件,有些情况要适当运用公式说明。
2.??
解:A、根据P=W/t,t不确定,W大的,功率不一定大,故A错误;
B、做功快的物体,其功率大,故B正确;
C、机械效率是有用功与总功的比值,总功不确定,机械效率不能确定,故C错误;
D、有用功不确定,总功不能确定,总功不确定,机械效率不能确定,故D错误。
故选:B。
(1)根据P=W/t,三个物理,要确定其中两个量的关系,必须保证另外一个量不变;
(2)总功=有用功+额外功;有用功和总功的比值叫机械效率;由机械效率的定义可知,机械效率的高低只与有用功在总功中所占的比例有关,比例越大,机械效率越高。
本题考查了功率、机械效率,利用控制变量法来讨论两个物理量之间的关系是本题的关键。
3.??
解:
A、因为功率就是描述物体做功快慢的物理量。做功快,功率一定大。故A正确;
B、物体做功多少与功率和时间都有关系。功率大,时间不确定,功率不能确定,因此机械效率不能确定。故B错误;
C、由于机械效率是有用功与总功的比值,做有用功多,机械效率不一定高。故C错误;
D、根据功的原理可知省力的机械不能省功,因此省力的机械,机械效率不一定越高。故D错误。
故选:A。
根据功、功率、机械效率的关系分析。功率是单位时间内做的功的多少,表示做功快慢的物理量;机械效率是有用功与总功的比值。
本题考查了功、功率、机械效率的关系。功率由功和时间共同决定,机械效率由有用功和总功共同决定。
4.??
解:
A、由题知,第二次匀速提升同样货物到相同的高度,因为两次匀速提升物体的速度大小关系未知,所以根据速度公式可知不能判断提升货物所用的时间,故A错误;
B、两次匀速同样的货物到相同高度,由W有=Gh可知,起重机两次做的有用功相等,故B错误;
CD、起重机经保养后,提高了机械效率,而起重机两次做的有用功相等,由η=W有用/W总可知,第二次做的总功较少,由W总=W有用+W额可知第二次做的额外功较少,故C正确、D错误。
故选:C。
(1)由题知,第二次匀速提升同样货物到相同的高度,两次匀速提升物体的速度大小关系未知,根据速度公式判断所用的时间;
(2)匀速提升同样货物到相同的高度,利用W有=Gh比较起重机两次做的有用功大小关系;
(3)起重机经保养后,提高了机械效率,而起重机两次做的有用功相等,利用η=W有用/W总比较两次做的总功大小关系,根据W总=W有用+W额可得两次做的额外功大小关系。
本题考查了功的公式、速度公式、机械效率公式的应用,注意:对于某机械来说,明确有用功、总功、额外功之间的关系是关键。
5.??
解:
A、由图可知,杠杆在使用的过程中,动力臂要大于阻力臂,所以是省力杠杆,故A正确;
B、所做的有用功为:W有用=Gh=24N×0.1m=2.4J;故B正确;
CD、如图所示:;
物体在5s内缓慢升高10cm,根据相似三角形的性质可知,拉力F的作用点上升的距离s=2×10cm=20cm=0.2m;
拉力所做的总功为:W总=Fs=16N×0.2m=3.2J;
额外功为:W额=W总-W有用=3.2J-2.4J=0.8J,故C正确,D错误。
故选:D。
(1)根据动力臂和阻力臂的大小判定杠杆的种类;
(2)根据W有用=Gh求出有用功;
(3)(4)根据相似三角形的性质判定拉力F的作用点上升的距离;根据W总=Fs求出总功,然后根据W总=W有用+W额求出额外功的大小;
本题考查了杠杆的分类、有用功、总功和额外功的计算,关键是求出拉力F的作用点上升的距离。
6.??
解:A、若物体运动的方向与受力方向垂直,则力对物体没有做功,故A错误;
B、功率大的机器做功快,故B正确;
C、做功快的机器只能说明功率大,而机械效率不一定高,故C错误;
D、功率小说明它做功慢,由W=Pt可知做功的多少由时间和功率共同决定,故D错误。
故选:B。
利用下列知识分析判断:
(1)做功的必要条件:有力作用在物体上,在力的方向上通过的距离;
(2)功率是单位时间内做的功的多少,功率大表示做功快;
(3)机械效率是有用功与总功的比值。
本题考查了功、功率、机械效率的关系。功率由功和时间共同决定,机械效率由有用功和总功共同决定。
7.??
解:A、根据公式W有用=Gh=mgh可知甲、乙吊车做的有用功相同,此选项错误,不符合题意;
B、已知甲吊车的机械效率高,有用功相同,甲吊车的总功较少,此选项错误,不符合题意;
C、两辆吊车做的有用功相同,乙的效率较低,所以乙吊车做的额外功较多,此选项正确,符合题意;
D、已知甲吊车的机械效率高,有用功相同,甲吊车的总功较少,此选项错误,不符合题意。
故选:C。
甲吊车的机械效率比乙吊车的机械效率高,说明甲吊车所做的有用功在总功中占的比值比乙吊车大;把相同质量的物体提高相同的高度,根据公式W有用=Gh=mgh可知:两辆吊车所做的有用功相同;机械效率不同,是因为做的额外功不同,导致总功不同。
此题考查机械效率公式和对有用功的理解。效率大小要根据计算公式η=W有用/W总判断。
8.??
解:
A、功率与机械效率无关,功率大,机械效率不一定高,故A错误;
B、减少了总功,由于不知道有用功的大小,无法确定机械效率的大小,故B错误;
C、额外功在总功中所占比例越小,则有用功与总功的比值越大,机械效率一定越高,故C正确;
D、机械效率的大小与省力情况无关,省力越多的机械,机械效率不一定高,故D错误。
故选:C。
①总功=有用功+额外功;
②有用功和总功的比值叫机械效率;
③由机械效率的定义可知,机械效率的高低只与有用功在总功中所占的比例有关,与做功多少、功率大小无关。
理解机械效率的定义,明确有用功、额外功和总功之间的关系是解决此类题目的关键。
9.??
解:A、机械效率跟物体移动的距离无关,故A错误。
B、减小动滑轮的重力,可以减小额外功,增大有用功在总功中所占的比例,可以提高机械效率,故B正确。
C、减小总功,不知道有用功的变化,不能确定机械效率的变化,故C错误。
D、机械效率跟外力无关,故D错误。
故选:B。
提高机械效率的方法:减小摩擦;减小机械重;增大提起的物体重力。机械效率高低跟物体移动的距离无关。
机械效率跟摩擦、机械重、提起的物体重力有关,跟其它因素没有关系。
10.??
解:
A、总功包括有用功和额外功,额外功在总功中占比例越小,则有用功在总功中占比例越大,机械效率越高,故A正确;
B、机械效率是有用功与总功之比:η=W有用/W总,机械功率是物体在单位时间内做的功,P=W/t,机械效率与机械功率大小没有直接关系,故B错误;
C、由W=Pt可知,做功多少还受时间的影响,功率不同的机器,做的功可能相等,故C错误;
D、功率是功与时间的比值,做功多,时间不确定,功率大小不能确定,故D错误。
故选:A。
(1)根据P=W/t,功率由功和时间共同决定;
(2)功率是表示做功快慢的物理量,机械效率是有用功和总功的比值。
该题考查学生对机械效率的理解,特别要注意功率与机械效率是两个不同的物理量,它们之间没有任何关系。
【填空题答案】
1.??4? 2.5W? 80???????
2.??1000? 100???????
1.??减小接触面的粗糙程度? 不省功???????
2.??1.2? 不能? 75%???????
1.??125? 80? 5???????
【解析】
1.??
解:
(1)拉力做的有用功:
W有用=Gh=10N×0.4m=4J;
(2)拉力做的总功:
W总=Fs=5N×1m=5J,
拉力做功功率:
P=2.5W;
(3)斜面的机械效率:
η=80%。
故答案为:4;2.5W;80。
(1)知道铁块重力和斜面高度,根据W=Gh求出有用功;
(2)知道拉力和斜面长,根据W=Fs求出总功;再利用P=W/t求拉力做功功率;
(3)求出了有用功、总功,斜面的机械效率等于有用功与总功之比。
知道斜面长、高、推力、物重,求出有用功和总功,根据机械效率公式求出机械效率,属于基础题目,明确有用功、总功的含义是关键。
2.??
解:推力所做的有用功:W有用=Gh=1000N×1m=1000J;
推力所做的总功:W总=Fs=300N×5m=1500J,
推力所做的额外功:W额=W总-W有用=1500J-1000J=500J,
由W额=fs可得,物体与斜面的摩擦力:
f=100N。
故答案为:1000;100。
(1)已知物体重力和提升的高度,根据公式W=Gh可求有用功;
(2)根据公式W=Fs可求总功,额外功等于总功减去有用功,利用W额=fs公式变形求摩擦力。
本题考查了有用功、总功、额外功的计算,关键是公式的灵活运用。
1.??
解:(1)斜面的机械效率与斜面的倾斜程度和摩擦有关,所以保持斜面倾斜程度不变,可以采用减小接触面的粗糙程度的方法减小摩擦,从而提高斜面的机械效率。
(2)实验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都不省功。
故答案为:(1)减小接触面的粗糙程度。(2)不省功。
(1)影响摩擦力大小的因素有:压力,接触面的粗糙程度.
(2)使用任何机械都不省功。
知道减小摩擦的方法,理解功的原理,可解答此题。
2.??
解:
(1)已知G=3N,h=0.4m,
所以克服物体重力所做的功是有用功:
W有=Gh=3N×0.4m=1.2J;
(2)已知F=2N,s=0.8m,
拉力做的功:
W总=Fs=2N×0.8m=1.6J;
分析数据可知利用斜面不能省功,
斜面的机械效率:
η=75%。
故答案为:1.2;不能;75%。
(1)克服物体重力所做的功是有用功,利用W=Gh计算拉力所做的有用功;
(2)使用任何机械都不省功,拉力所做的功是总功,利用W=Fs计算拉力所做的功;机械效率等于有用功与总功的比值。
此题考查了功的计算与斜面的机械效率,同时也明确了斜面也是一种省力的机械,任何机械省力但不省功。
1.??
解:
(1)推力做功:W总=Fs=25N×10m=250J,
推力对箱子做功功率:P=125W;
(2)推力对箱子做的有用功:W有=Gh=100N×2m=200J,
斜面的机械效率:η=80%。
(3)额外功:W额=W总-W有=250J-200J=50J,
则箱子受到斜面摩擦力f=5W。
故答案为:125;80;5。
(1)利用W=Fs计算推力做功,利用P=W/t求推力的功率。
(2)知道斜面长和沿斜面推力大小,利用W=Fs求推力对箱子做的功(总功);利用W=Gh求推力对箱子做的有用功,再利用效率公式求斜面的机械效率。
本题考查了使用斜面有用功、总功、额外功、功率、机械效率的计算,本题关键在于确定有用功和总功,将箱子提升2m做的功为有用功。
【探究题简答题计算题答案】
1.??0.7? 0.6? 71.4? B? 当其它条件一定时,斜面倾斜程度越大,斜面的机械效率越高? 倾斜程度? 粗糙程度???????
2.??便于测量力臂以及消除杠杆自重的影响? 3? 先变小后变大? 没有消除杠杆自身重力的影响? 0.5? 66.7? 不变? 变大???????
1.??答:在登山时,盘山的大路和走小路,根据功的原理可知都不会省功,但在做功一定的条件下,走小路通过费力达到省距离的目的,盘山大路虽然是斜面,沿大路走,虽然省力但增加了距离。???????
2.??解:根据功的原理,使用任何机械都不省功,因此无论使用哪种机械,都不省功。所以左面小孩的说法不正确;
而左面小孩的提升方案中,额外功存在,故机械效率不会很高,右面小孩的提升方案中,额外功很小,故机械效率高;所以我们应支持右面小孩的说法。
答:支持右面小孩的说法;不支持左面小孩的原因:(1)使用任何机械都不省功;(2)使用机械要多做额外功,机械效率会更低。???????
1.??解:(1)木箱的重力:G=1200N,
工人师傅对木箱做的有用功:W有用=Gh=1200N×1m=1200J;
(2)拉力做的总功:W总=Fs=300N×6m=1800J。
克服摩擦力所做的额外功:
W额=W总-W有=1800J-1200J=600J,
由W额=fs可得,物体所受斜面的摩擦力:
f=100N。
答:(1)工人所做的有用功是1200J;
(2)物体所受斜面的摩擦力是100N。???????
【解析】
1.??
解:(1)由表格数据可知,实验③数据中的有用功W有3=G3h3=1N×0.7m=0.7J,
实验②数据中的总功W总2=F2s2=0.6N×1m=0.6J,
实验①数据中的机械效率η≈71.4%;
(2)通过对比实验①②数据可知,斜面的倾角和长度、物重相同,斜面粗糙程度不同,斜面的机械效率不同,故可得结论:斜面的机械效率跟斜面的粗糙程度有关,可验证猜想B;
(3)通过对比实验①③数据可知,斜面的粗糙程度和长度、物重相同,斜面倾角不同,斜面的机械效率不同,且斜面倾角越大,斜面的机械效率越高,故可得结论:当其它条件一定时,斜面倾斜程度越大,斜面的机械效率越高;
(4)若要验证斜面的机械效率跟物体的重力有关,应控制斜面的倾斜程度和粗糙程度、长度不变,改变物体的重力。
故答案为:(1)0.7;0.6;71.4;(2)B;(3)当其它条件一定时,斜面倾斜程度越大,斜面的机械效率越高;(4)倾斜程度;粗糙程度。
(1)根据表格数据结合W=Gh求出有用功、根据W=Fs求出总功、利用η求出斜面的机械效率;
(2)由猜想可知,斜面的机械效率可能跟斜面的倾斜程度、斜面的粗糙程度、斜面的长度、物体的重力有关,研究与其中一个因素的关系时,要控制另外的因素不变;
对比实验①②数据,根据控制变量法,找出相同量和变化的量,分析得出验证的猜想;
(3)通过对比实验①③数据,根据控制变量法,找出相同量和变化的量,分析得出探究结论;
(4)根据控制变量法,研究机械效率跟物体的重力有关,要控制其它因素相同。
本题研究斜面的机械效率跟什么因素有关的实验,涉及到有用功、总功、机械效率的计算,会利用控制变量法分析实验数据得出结论是关键。
2.??
解:(1)将杠杆的中点O挂在支架上,调节杠杆两端螺母使杠杆在水平位置平衡,目的是便于测量力臂以及消除杠杆自重的影响;
(2)设杠杆的一个小格为L,一个钩码重为G,因为F1L1=F2L2,所以2G×3L=nG×2L,解得n=3,所以在A处挂3个钩码,使杠杆在水平位置平衡;
(3)由图可知,OC为最长力臂,当弹簧测力计由位置1转至位置2的过程中,动力臂先变长后变短,而杠杆在水平位置始终保持平衡,根据杠杆平衡条件可知,测力计示数将先变小后变大;
(4)把支点选到B点,杠杆的重心在O点,在计算时,由于杠杆自身重力的影响,左边应有两个力,故此时不满足杠杆平衡条件;
(5)完成以上实验后,小明利用杠杆来测量测量杠杆的机械效率,实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升,由图知,拉力F=0.5N。
有用功是:W有用=Gh=1N×0.1m=0.1J,
总功是:W总=Fs=0.5N×0.3m=0.15J,
所以杠杆的机械效率是η=66.7%;
将钩码的悬挂点由A移至B,O、C位置不变,仍将钩码提升相同的高度,有用功不变;由于额外功是提升杠杆所做的功,悬挂点由A移至B后,杠杆实际提升的高度变小,所以额外功也变小,则总功变小,所以杠杆的机械效率将变大。
故答案为:(1)便于测量力臂以及消除杠杆自重的影响;(2)3;(3)先变小后变大;(4)没有消除杠杆自身重力的影响;(5)0.5;66.7%;不变;变大。
(1)(4)为了便于测量力臂大小,需将杠杆在水平位置平衡,将杠杆中点作为杠杆支点可以消除杠杆自身重力对杠杆平衡的影响;
(2)(3)根据杠杆的平衡条件分析解答;
(5)有用功与总功的比值是机械效率。
本题考查探究杠杆平衡条件的实验及杠杆机械效率的测量,关键是将课本知识内容记忆清楚,仔细分析即可。
1.??
首先知道功的原理:使用任何机械都不会省功,省力的机械费距离,费力的机械省距离;然后根据我们登山和车走盘山路的目的分析解答。
解决此类问题的关键是知道使用机械是为了方便、为了省力、还可能是为了省距离等,但都不会省功。
2.??
本题首先根据功的原理(使用任何机械都不省功)判断出合理的说法;然后根据提升机械效率的方法(一是在机械装置相同时,增加有用功,即提更重的重物;二是减少额外功)进行分析。
本题考查功的原理的应用,一定记住:使用任何机械,额外功都存在,都能不省功。
1.??
(1)知道木箱的重力和斜面的高度,根据W=Gh求出克服重力做的有用功;
(2)已知拉力F与斜面长,利用W=Fs计算总功,总功减去有用功即为克服摩擦力所做的额外功,根据W额=fs求出物体所受斜面的摩擦力。
本题考查了做功公式和机械效率公式、重力公式的应用,明确有用功和额外功以及总功是关键。
一、单选题
1.???下列关于功、功率、机械效率的说法中正确的是( )
A.?机械效率越高,机械做功一定越快????????????????????????????????????????
B.?越省力的机械,其机械效率一定越高????????????????????????????????????????
C.?做功越慢的机械,功率一定越小????????????????????????????????????????
D.?功率不同的机器,做的功一定不相等
2.???下列关于功率和机械效率说法中正确的是( )
A.?做功多的物体,功率一定大????????????????????????????????????????
B.?做功快的物体,功率一定大????????????????????????????????????????
C.?有用功越大,机械的效率就越高????????????????????????????????????????
D.?额外功越大,机械的效率就越低
3.???关于功率和机械效率,下列说法正确的是( )
A.?功率大的机械,做功一定快????????????????????????????????????????
B.?功率大的机械,机械效率一定高????????????????????????????????????????
C.?做的有用功多,机械效率一定高????????????????????????????????????????
D.?省力的机械,机械效率一定高
4.???某起重机把货物匀速提升到三楼,用时为t1;起重机经保养后,提高了机械效率,当匀速提升同样货物到相同的高度,用时为t2,与第一次提升相比,第二次( )
A.?t2<t1?????????????????????????
B.?有用功较多?????????????????????????
C.?额外功较少?????????????????????????
D.?总功较多
5.???如图所示,质量分布均匀的杠杆在中点处悬挂一重力为24N的物体,用大小为16N的拉力F竖直向上匀速拉动杆,使物体在5s内缓慢升高10cm。若不计一切摩擦及阻力,下列说法错误的是( )
A.?这是一个省力杠杆????????????????????????????????????????
B.?整个过程中,所做的有用功为2.4J????????????????????????????????????????
C.?整个过程中,所做的额外功为0.8J????????????????????????????????????????
D.?整个过程中,拉力F的作用点上升的距离为5cm
6.???关于功、功率、机械效率,下列说法中正确的是( )
A.?物体受力且运动时,力对物体就做了功????????????????????????????????????????
B.?功率大的机器做功就快????????????????????????????????????????
C.?做功快的机器其机械效率一定高????????????????????????????????????????
D.?功率小的机器做功一定少
7.???甲吊车比乙吊车的机械效率高,当它们分别把相同质量的物体匀速提升相同高度时,则( )
A.?甲吊车的电动机做的有用功较多????????????????????????????????????????
B.?甲吊车的电动机做的总功较多????????????????????????????????????????
C.?乙吊车的电动机做的额外功较多????????????????????????????????????????
D.?甲、乙两吊车的电动机做的总功相同
8.???下面说法正确的是( )
A.?功率越大的机械,机械效率越高????????????????????????????????????????
B.?减少了总功,就能提高机械效率????????????????????????????????????????
C.?额外功在总功中所占比例越小,机械效率一定越高????????????????????????????????????????
D.?省力越多的机械,机械效率一定越高
9.???要提高某机械的机械效率,应该( )
A.?减小外力所移动的距离?????????????????????????
B.?减小动滑轮的质量?????????????????????????
C.?减小总功?????????????????????????
D.?减小外力
10.???下列关于功、功率、机械效率的说法正确的是( )
A.?额外功与总功之比越小,机械效率一定越大????????????????????????????????????????
B.?机器的功率越小,机械效率一定越低????????????????????????????????????????
C.?功率不同的机器,做的功一定不相等????????????????????????????????????????
D.?物体做功越多,功率一定越大
二、填空题
1.???如图所示,斜面长1m,高0.4m,用大小为5N沿斜面向上的拉力F,经2秒钟将重10N的铁块从底端匀速拉到顶端,在该过程中,有用功为______J;拉力做功的功率为______;斜面的机械效率为______%
???如图所示,工人用平行于斜面的推力,把一个重为1000N的物体,沿着长5m、高1m的斜面由底端匀速推到顶端,推力的大小为300N,则推力所做的有用功为______J,物体与斜面的摩擦力为______N。
???在日常生活和工农业生产中,提高机械效率有着重要的意义。小亮利用如图装置测斜面的机械效率。斜面的机械效率与斜面的倾斜程度和摩擦有关,与物重无关。
(1)保持斜面倾斜程度不变,可以采用______的方法减小摩擦,从而提高斜面的机械效率。
(2)实验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都______。
???如图所示,将一个重3N的物体匀速拉到斜面顶端,人沿斜面向上的拉力为2N,物体沿斜面移动的距离为0.8m,上升的高度为0.4m,则物体重力做功为______J,分析数据可知利用斜面______(能/不能)省功,斜面的机械效率是______。
5.???如图,斜面长10m、高2m,工人用沿斜面向上25N的力,用了2s把重100N的箱子匀速推到车上,则推力的功率是______W;该斜面机械效率是______%。箱子受到斜面摩擦力是______N.
三、实验探究题
1.???学习了机械效率知识后,全班同学对“斜面的机械效率跟什么因素有关”这一课题提出了一些值得探究的猜想:A、斜面的机械效率跟斜面的倾斜程度有关;B、跟斜面的粗糙程度有关;C、跟斜面的长度有关;D、跟物体的重力有关。小明同学为了证实其中的部分猜想是否正确,设计方案并进行了探究,他的探究实验数据如下表。
实验次数
斜面倾角
斜面粗糙程度
物重
G/N
斜面高度
h/m
沿斜面拉力
F/N
斜面长
s/m
有用功
W有/J
总功
W总/J
机械效率
η(%)
①
30°
粗糙
1
0.5
0.7
1
0.5
0.7
②
30°
稍光滑
1
0.5
0.6
1
0.5
83.3
③
45°
粗糙同①
1
0.7
0.9
1
0.9
77.8
(1)请你替小明在上表中的空格处填上适当的数据W有______、W总______、η=______(保留一位小数)
(2)通过对比实验①②数据,可验证猜想______(填写字母)。
(3)通过对比实验①③数据,可以得出的探究结论是:______。
(4)若要验证猜想D,应控制斜面的长、斜面的______和______不改变。
2.???在探究“杠杆平衡条件”实验中(每个钩码质量相等,杠杆上每小格等距):
?(1)将杠杆的中点O挂在支架上后,调节杠杆两端螺母使杠杆在水平位置平衡,目的是______;
(2)杠杆平衡后,小明同学在图甲所示的A位置挂上两个钩码,可在B位置挂上______个钩码,使杠杆在水平位置平衡;
(3)取下B位置的钩码,改用弹簧测力计拉杠杆的C点使杠杆在水平位置保持平衡。当弹簧测力计由位置1转至位置2的过程中,杠杆在水平位置始终保持平衡(如图乙),测力计示数将______(选填“一直变大”、“一直变小”、“先变大后变小”、“先变小后变大”);
(4)接着小明把支点选到B点,如图丙,在A点挂一个钩码,在C点挂3个钩码,杠杆也恰好水平静止,她觉得此时不满足杠杆平衡条件,造成这个问题的原因是______;
(5)完成以上实验后,小明利用杠杆来测量测量杠杆的机械效率。如图丁,实验时,竖直向上拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。实验中,将杠杆拉至图中虚线位置测力计的示数F=______N,钩码总重G为1.0N,钩码上升高度h为0.1m,测力计移动距离s为0.3m,则杠杆的机械效率为______%(结果精确到0.1%)。如果把钩码由A移至B,两次实验A点竖直移动相同距离,拉力所做的有用功将______,此杠杆的机械效率将______(两空均选填“变大”、“变小”或“不变”)。
四、简答题
1.???功的原理告诉我们:使用机械可以省力,不能省功。我们登山时,常常爱走小路,不喜欢走大路,盘山的大路都是斜面,难道不省力吗?
2.???如图所示,两小儿之辩,关于机械省力,省功以及机械效率的辩论,你支持哪一方的说法?不支持另外一方的原因是什么?
五、计算题
1.???工人师傅要将重为1200N的木箱搬到1m高的车厢里.他将一块6m长的木板搁在地面与车厢之间构成斜面,然后站在车上用300N的拉力将物体从斜面底端匀速拉到车厢里,如图所示,求:
(1)工人所做的有用功。
(2)物体所受斜面的摩擦力。
第9章 五、探究——使用机械是否省功
【答案】
1.??C???????2.??B???????3.??A???????4.??C???????5.??D???????
6.??B???????7.??C???????8.??C???????9.??B???????10.??A???????
【解析】
1.??
解:A、机械效率是指有用功与总功的比值,功率反应物体做功的快慢,机械效率与机械功率大小没有直接关系,故A错误;
B、机械效率是有用功与总功的比值,与机械的省力情况无关,故B错误;
C、功率反映做功的快慢,功率大则做功快,功率小说明做功慢,故C正确;
D、功率不同的机械,做的功有可能相等。如功率为5000W的机械60s做的功与功率为1000W的机械300s做的功相同,故D错误。
故选:C。
①功率是描述物体做功快慢的物理量,它等于单位时间内所做的功,功率大则做功快;
②机械效率反映了机械的性能优劣,是有用功与总功的比值;
③机械效率与机械做功功率和机械的省力情况无关。
深刻理解功率和机械效率的概念是解决此题的关键,要充分考虑选项中的条件,有些情况要适当运用公式说明。
2.??
解:A、根据P=W/t,t不确定,W大的,功率不一定大,故A错误;
B、做功快的物体,其功率大,故B正确;
C、机械效率是有用功与总功的比值,总功不确定,机械效率不能确定,故C错误;
D、有用功不确定,总功不能确定,总功不确定,机械效率不能确定,故D错误。
故选:B。
(1)根据P=W/t,三个物理,要确定其中两个量的关系,必须保证另外一个量不变;
(2)总功=有用功+额外功;有用功和总功的比值叫机械效率;由机械效率的定义可知,机械效率的高低只与有用功在总功中所占的比例有关,比例越大,机械效率越高。
本题考查了功率、机械效率,利用控制变量法来讨论两个物理量之间的关系是本题的关键。
3.??
解:
A、因为功率就是描述物体做功快慢的物理量。做功快,功率一定大。故A正确;
B、物体做功多少与功率和时间都有关系。功率大,时间不确定,功率不能确定,因此机械效率不能确定。故B错误;
C、由于机械效率是有用功与总功的比值,做有用功多,机械效率不一定高。故C错误;
D、根据功的原理可知省力的机械不能省功,因此省力的机械,机械效率不一定越高。故D错误。
故选:A。
根据功、功率、机械效率的关系分析。功率是单位时间内做的功的多少,表示做功快慢的物理量;机械效率是有用功与总功的比值。
本题考查了功、功率、机械效率的关系。功率由功和时间共同决定,机械效率由有用功和总功共同决定。
4.??
解:
A、由题知,第二次匀速提升同样货物到相同的高度,因为两次匀速提升物体的速度大小关系未知,所以根据速度公式可知不能判断提升货物所用的时间,故A错误;
B、两次匀速同样的货物到相同高度,由W有=Gh可知,起重机两次做的有用功相等,故B错误;
CD、起重机经保养后,提高了机械效率,而起重机两次做的有用功相等,由η=W有用/W总可知,第二次做的总功较少,由W总=W有用+W额可知第二次做的额外功较少,故C正确、D错误。
故选:C。
(1)由题知,第二次匀速提升同样货物到相同的高度,两次匀速提升物体的速度大小关系未知,根据速度公式判断所用的时间;
(2)匀速提升同样货物到相同的高度,利用W有=Gh比较起重机两次做的有用功大小关系;
(3)起重机经保养后,提高了机械效率,而起重机两次做的有用功相等,利用η=W有用/W总比较两次做的总功大小关系,根据W总=W有用+W额可得两次做的额外功大小关系。
本题考查了功的公式、速度公式、机械效率公式的应用,注意:对于某机械来说,明确有用功、总功、额外功之间的关系是关键。
5.??
解:
A、由图可知,杠杆在使用的过程中,动力臂要大于阻力臂,所以是省力杠杆,故A正确;
B、所做的有用功为:W有用=Gh=24N×0.1m=2.4J;故B正确;
CD、如图所示:;
物体在5s内缓慢升高10cm,根据相似三角形的性质可知,拉力F的作用点上升的距离s=2×10cm=20cm=0.2m;
拉力所做的总功为:W总=Fs=16N×0.2m=3.2J;
额外功为:W额=W总-W有用=3.2J-2.4J=0.8J,故C正确,D错误。
故选:D。
(1)根据动力臂和阻力臂的大小判定杠杆的种类;
(2)根据W有用=Gh求出有用功;
(3)(4)根据相似三角形的性质判定拉力F的作用点上升的距离;根据W总=Fs求出总功,然后根据W总=W有用+W额求出额外功的大小;
本题考查了杠杆的分类、有用功、总功和额外功的计算,关键是求出拉力F的作用点上升的距离。
6.??
解:A、若物体运动的方向与受力方向垂直,则力对物体没有做功,故A错误;
B、功率大的机器做功快,故B正确;
C、做功快的机器只能说明功率大,而机械效率不一定高,故C错误;
D、功率小说明它做功慢,由W=Pt可知做功的多少由时间和功率共同决定,故D错误。
故选:B。
利用下列知识分析判断:
(1)做功的必要条件:有力作用在物体上,在力的方向上通过的距离;
(2)功率是单位时间内做的功的多少,功率大表示做功快;
(3)机械效率是有用功与总功的比值。
本题考查了功、功率、机械效率的关系。功率由功和时间共同决定,机械效率由有用功和总功共同决定。
7.??
解:A、根据公式W有用=Gh=mgh可知甲、乙吊车做的有用功相同,此选项错误,不符合题意;
B、已知甲吊车的机械效率高,有用功相同,甲吊车的总功较少,此选项错误,不符合题意;
C、两辆吊车做的有用功相同,乙的效率较低,所以乙吊车做的额外功较多,此选项正确,符合题意;
D、已知甲吊车的机械效率高,有用功相同,甲吊车的总功较少,此选项错误,不符合题意。
故选:C。
甲吊车的机械效率比乙吊车的机械效率高,说明甲吊车所做的有用功在总功中占的比值比乙吊车大;把相同质量的物体提高相同的高度,根据公式W有用=Gh=mgh可知:两辆吊车所做的有用功相同;机械效率不同,是因为做的额外功不同,导致总功不同。
此题考查机械效率公式和对有用功的理解。效率大小要根据计算公式η=W有用/W总判断。
8.??
解:
A、功率与机械效率无关,功率大,机械效率不一定高,故A错误;
B、减少了总功,由于不知道有用功的大小,无法确定机械效率的大小,故B错误;
C、额外功在总功中所占比例越小,则有用功与总功的比值越大,机械效率一定越高,故C正确;
D、机械效率的大小与省力情况无关,省力越多的机械,机械效率不一定高,故D错误。
故选:C。
①总功=有用功+额外功;
②有用功和总功的比值叫机械效率;
③由机械效率的定义可知,机械效率的高低只与有用功在总功中所占的比例有关,与做功多少、功率大小无关。
理解机械效率的定义,明确有用功、额外功和总功之间的关系是解决此类题目的关键。
9.??
解:A、机械效率跟物体移动的距离无关,故A错误。
B、减小动滑轮的重力,可以减小额外功,增大有用功在总功中所占的比例,可以提高机械效率,故B正确。
C、减小总功,不知道有用功的变化,不能确定机械效率的变化,故C错误。
D、机械效率跟外力无关,故D错误。
故选:B。
提高机械效率的方法:减小摩擦;减小机械重;增大提起的物体重力。机械效率高低跟物体移动的距离无关。
机械效率跟摩擦、机械重、提起的物体重力有关,跟其它因素没有关系。
10.??
解:
A、总功包括有用功和额外功,额外功在总功中占比例越小,则有用功在总功中占比例越大,机械效率越高,故A正确;
B、机械效率是有用功与总功之比:η=W有用/W总,机械功率是物体在单位时间内做的功,P=W/t,机械效率与机械功率大小没有直接关系,故B错误;
C、由W=Pt可知,做功多少还受时间的影响,功率不同的机器,做的功可能相等,故C错误;
D、功率是功与时间的比值,做功多,时间不确定,功率大小不能确定,故D错误。
故选:A。
(1)根据P=W/t,功率由功和时间共同决定;
(2)功率是表示做功快慢的物理量,机械效率是有用功和总功的比值。
该题考查学生对机械效率的理解,特别要注意功率与机械效率是两个不同的物理量,它们之间没有任何关系。
【填空题答案】
1.??4? 2.5W? 80???????
2.??1000? 100???????
1.??减小接触面的粗糙程度? 不省功???????
2.??1.2? 不能? 75%???????
1.??125? 80? 5???????
【解析】
1.??
解:
(1)拉力做的有用功:
W有用=Gh=10N×0.4m=4J;
(2)拉力做的总功:
W总=Fs=5N×1m=5J,
拉力做功功率:
P=2.5W;
(3)斜面的机械效率:
η=80%。
故答案为:4;2.5W;80。
(1)知道铁块重力和斜面高度,根据W=Gh求出有用功;
(2)知道拉力和斜面长,根据W=Fs求出总功;再利用P=W/t求拉力做功功率;
(3)求出了有用功、总功,斜面的机械效率等于有用功与总功之比。
知道斜面长、高、推力、物重,求出有用功和总功,根据机械效率公式求出机械效率,属于基础题目,明确有用功、总功的含义是关键。
2.??
解:推力所做的有用功:W有用=Gh=1000N×1m=1000J;
推力所做的总功:W总=Fs=300N×5m=1500J,
推力所做的额外功:W额=W总-W有用=1500J-1000J=500J,
由W额=fs可得,物体与斜面的摩擦力:
f=100N。
故答案为:1000;100。
(1)已知物体重力和提升的高度,根据公式W=Gh可求有用功;
(2)根据公式W=Fs可求总功,额外功等于总功减去有用功,利用W额=fs公式变形求摩擦力。
本题考查了有用功、总功、额外功的计算,关键是公式的灵活运用。
1.??
解:(1)斜面的机械效率与斜面的倾斜程度和摩擦有关,所以保持斜面倾斜程度不变,可以采用减小接触面的粗糙程度的方法减小摩擦,从而提高斜面的机械效率。
(2)实验表明:额外功越小,总功越接近有用功;进一步推理得出:假设没有额外功,总功等于有用功;可见使用任何机械都不省功。
故答案为:(1)减小接触面的粗糙程度。(2)不省功。
(1)影响摩擦力大小的因素有:压力,接触面的粗糙程度.
(2)使用任何机械都不省功。
知道减小摩擦的方法,理解功的原理,可解答此题。
2.??
解:
(1)已知G=3N,h=0.4m,
所以克服物体重力所做的功是有用功:
W有=Gh=3N×0.4m=1.2J;
(2)已知F=2N,s=0.8m,
拉力做的功:
W总=Fs=2N×0.8m=1.6J;
分析数据可知利用斜面不能省功,
斜面的机械效率:
η=75%。
故答案为:1.2;不能;75%。
(1)克服物体重力所做的功是有用功,利用W=Gh计算拉力所做的有用功;
(2)使用任何机械都不省功,拉力所做的功是总功,利用W=Fs计算拉力所做的功;机械效率等于有用功与总功的比值。
此题考查了功的计算与斜面的机械效率,同时也明确了斜面也是一种省力的机械,任何机械省力但不省功。
1.??
解:
(1)推力做功:W总=Fs=25N×10m=250J,
推力对箱子做功功率:P=125W;
(2)推力对箱子做的有用功:W有=Gh=100N×2m=200J,
斜面的机械效率:η=80%。
(3)额外功:W额=W总-W有=250J-200J=50J,
则箱子受到斜面摩擦力f=5W。
故答案为:125;80;5。
(1)利用W=Fs计算推力做功,利用P=W/t求推力的功率。
(2)知道斜面长和沿斜面推力大小,利用W=Fs求推力对箱子做的功(总功);利用W=Gh求推力对箱子做的有用功,再利用效率公式求斜面的机械效率。
本题考查了使用斜面有用功、总功、额外功、功率、机械效率的计算,本题关键在于确定有用功和总功,将箱子提升2m做的功为有用功。
【探究题简答题计算题答案】
1.??0.7? 0.6? 71.4? B? 当其它条件一定时,斜面倾斜程度越大,斜面的机械效率越高? 倾斜程度? 粗糙程度???????
2.??便于测量力臂以及消除杠杆自重的影响? 3? 先变小后变大? 没有消除杠杆自身重力的影响? 0.5? 66.7? 不变? 变大???????
1.??答:在登山时,盘山的大路和走小路,根据功的原理可知都不会省功,但在做功一定的条件下,走小路通过费力达到省距离的目的,盘山大路虽然是斜面,沿大路走,虽然省力但增加了距离。???????
2.??解:根据功的原理,使用任何机械都不省功,因此无论使用哪种机械,都不省功。所以左面小孩的说法不正确;
而左面小孩的提升方案中,额外功存在,故机械效率不会很高,右面小孩的提升方案中,额外功很小,故机械效率高;所以我们应支持右面小孩的说法。
答:支持右面小孩的说法;不支持左面小孩的原因:(1)使用任何机械都不省功;(2)使用机械要多做额外功,机械效率会更低。???????
1.??解:(1)木箱的重力:G=1200N,
工人师傅对木箱做的有用功:W有用=Gh=1200N×1m=1200J;
(2)拉力做的总功:W总=Fs=300N×6m=1800J。
克服摩擦力所做的额外功:
W额=W总-W有=1800J-1200J=600J,
由W额=fs可得,物体所受斜面的摩擦力:
f=100N。
答:(1)工人所做的有用功是1200J;
(2)物体所受斜面的摩擦力是100N。???????
【解析】
1.??
解:(1)由表格数据可知,实验③数据中的有用功W有3=G3h3=1N×0.7m=0.7J,
实验②数据中的总功W总2=F2s2=0.6N×1m=0.6J,
实验①数据中的机械效率η≈71.4%;
(2)通过对比实验①②数据可知,斜面的倾角和长度、物重相同,斜面粗糙程度不同,斜面的机械效率不同,故可得结论:斜面的机械效率跟斜面的粗糙程度有关,可验证猜想B;
(3)通过对比实验①③数据可知,斜面的粗糙程度和长度、物重相同,斜面倾角不同,斜面的机械效率不同,且斜面倾角越大,斜面的机械效率越高,故可得结论:当其它条件一定时,斜面倾斜程度越大,斜面的机械效率越高;
(4)若要验证斜面的机械效率跟物体的重力有关,应控制斜面的倾斜程度和粗糙程度、长度不变,改变物体的重力。
故答案为:(1)0.7;0.6;71.4;(2)B;(3)当其它条件一定时,斜面倾斜程度越大,斜面的机械效率越高;(4)倾斜程度;粗糙程度。
(1)根据表格数据结合W=Gh求出有用功、根据W=Fs求出总功、利用η求出斜面的机械效率;
(2)由猜想可知,斜面的机械效率可能跟斜面的倾斜程度、斜面的粗糙程度、斜面的长度、物体的重力有关,研究与其中一个因素的关系时,要控制另外的因素不变;
对比实验①②数据,根据控制变量法,找出相同量和变化的量,分析得出验证的猜想;
(3)通过对比实验①③数据,根据控制变量法,找出相同量和变化的量,分析得出探究结论;
(4)根据控制变量法,研究机械效率跟物体的重力有关,要控制其它因素相同。
本题研究斜面的机械效率跟什么因素有关的实验,涉及到有用功、总功、机械效率的计算,会利用控制变量法分析实验数据得出结论是关键。
2.??
解:(1)将杠杆的中点O挂在支架上,调节杠杆两端螺母使杠杆在水平位置平衡,目的是便于测量力臂以及消除杠杆自重的影响;
(2)设杠杆的一个小格为L,一个钩码重为G,因为F1L1=F2L2,所以2G×3L=nG×2L,解得n=3,所以在A处挂3个钩码,使杠杆在水平位置平衡;
(3)由图可知,OC为最长力臂,当弹簧测力计由位置1转至位置2的过程中,动力臂先变长后变短,而杠杆在水平位置始终保持平衡,根据杠杆平衡条件可知,测力计示数将先变小后变大;
(4)把支点选到B点,杠杆的重心在O点,在计算时,由于杠杆自身重力的影响,左边应有两个力,故此时不满足杠杆平衡条件;
(5)完成以上实验后,小明利用杠杆来测量测量杠杆的机械效率,实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升,由图知,拉力F=0.5N。
有用功是:W有用=Gh=1N×0.1m=0.1J,
总功是:W总=Fs=0.5N×0.3m=0.15J,
所以杠杆的机械效率是η=66.7%;
将钩码的悬挂点由A移至B,O、C位置不变,仍将钩码提升相同的高度,有用功不变;由于额外功是提升杠杆所做的功,悬挂点由A移至B后,杠杆实际提升的高度变小,所以额外功也变小,则总功变小,所以杠杆的机械效率将变大。
故答案为:(1)便于测量力臂以及消除杠杆自重的影响;(2)3;(3)先变小后变大;(4)没有消除杠杆自身重力的影响;(5)0.5;66.7%;不变;变大。
(1)(4)为了便于测量力臂大小,需将杠杆在水平位置平衡,将杠杆中点作为杠杆支点可以消除杠杆自身重力对杠杆平衡的影响;
(2)(3)根据杠杆的平衡条件分析解答;
(5)有用功与总功的比值是机械效率。
本题考查探究杠杆平衡条件的实验及杠杆机械效率的测量,关键是将课本知识内容记忆清楚,仔细分析即可。
1.??
首先知道功的原理:使用任何机械都不会省功,省力的机械费距离,费力的机械省距离;然后根据我们登山和车走盘山路的目的分析解答。
解决此类问题的关键是知道使用机械是为了方便、为了省力、还可能是为了省距离等,但都不会省功。
2.??
本题首先根据功的原理(使用任何机械都不省功)判断出合理的说法;然后根据提升机械效率的方法(一是在机械装置相同时,增加有用功,即提更重的重物;二是减少额外功)进行分析。
本题考查功的原理的应用,一定记住:使用任何机械,额外功都存在,都能不省功。
1.??
(1)知道木箱的重力和斜面的高度,根据W=Gh求出克服重力做的有用功;
(2)已知拉力F与斜面长,利用W=Fs计算总功,总功减去有用功即为克服摩擦力所做的额外功,根据W额=fs求出物体所受斜面的摩擦力。
本题考查了做功公式和机械效率公式、重力公式的应用,明确有用功和额外功以及总功是关键。
