沪科版(2012)初中数学九年级下册 24.7弧长与扇形面积 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 24.7弧长与扇形面积 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 918.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 08:40:22 | ||
图片预览

文档简介
24.7 弧长与扇形面积(1)
教学目标
(一)知识与技能:
1、了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用.
2、通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长L=和扇形面积S扇=的计算公式,并应用这些公式解决一些题目.
(二)过程与方法:
经历探索弧长和扇形面积的计算公式,培养学生合情推理和逻辑推理能力。
(三)情感、态度与价值观:在探索活动中,增强发现问题、解决问题的意识和养成合作交流的习惯.
教学重难点、关键
重点:n°的圆心角所对的弧长L=,扇形面积S扇=及其它们的应用.
2.难点:两个公式的应用.
3.关键:由圆的周长和面积迁移到弧长和扇形面积公式的过程.
教具、学具准备
小黑板、圆规、直尺、量角器、纸板.
教学过程
一、回顾复习
圆的周长公式:C=2πr.
圆的面积公式:S=πr2.
这里的π=30141592……,是个无理数,叫做圆周率。
情境引入
如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗?
新知探究
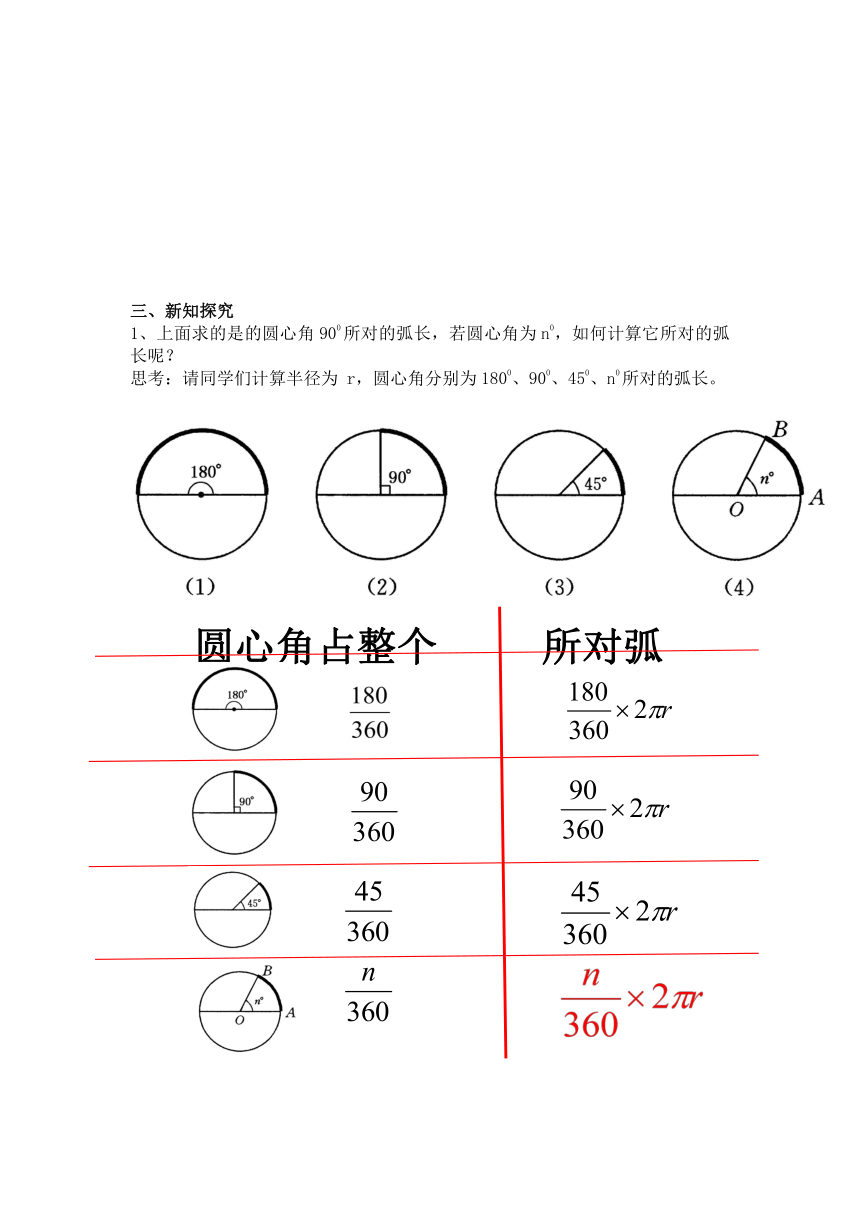
1、上面求的是的圆心角900所对的弧长,若圆心角为n0,如何计算它所对的弧长呢?
思考:请同学们计算半径为
r,圆心角分别为1800、900、450、n0所对的弧长。
结论:如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为:
练一练:已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度。
解:
答:此圆弧的长度为
如图,由组成圆心角的两条半径和圆心角所对的弧所围成
的图形叫扇形.
怎样计算圆心角是n0的扇形面积?
结论:如果扇形面积为s,圆心角度数为n,圆半径是r,那么扇形面积计算公式为
所以
举例应用
例1
一滑轮起重机装置(如图),滑轮的半径r=10cm,当重物上升15.7cm时,滑轮的一条半径OA绕轴心O逆时针方向旋转多少度?(假设绳索与滑轮之间没有滑动,π取3.14)
解:设半径OA绕轴心O逆时针方向旋转的度数为n°。
n≈90o
因而,旋转的角度约为90°.
例2
如图,圆心角为60°的扇形的半径为10厘米,求这个扇形的面积和周长.(π≈3.14)
解:因为n=60°,r=10厘米,所以扇形面积为
扇形的周长为
随堂练习
1.如果扇形的圆心角是230°,那么这个扇形的面积等于这个扇形所在圆的面积的(
)
2.扇形的面积是它所在圆的面积的
,这个扇形的圆心角的度数是_________°.
3.扇形的面积是S,它的半径是r,这个扇形的弧长是(
)
4.已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形=____.
5.已知扇形面积为____,圆心角为60°,则这个扇形的半径R=____.
6.已知半径为2cm的扇形,其弧长为_________
,则这个扇形的面积是_________.
7.如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为120°,OC长为8cm,CA长为12cm,则贴纸部分的面积为(
)
小结
(一
)
弧长的计算公式
(二)
扇形面积计算公式
布置作业
1.课本56面练习第1、2题。
2.预习圆柱和圆锥的侧面展开图。
教学目标
(一)知识与技能:
1、了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用.
2、通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长L=和扇形面积S扇=的计算公式,并应用这些公式解决一些题目.
(二)过程与方法:
经历探索弧长和扇形面积的计算公式,培养学生合情推理和逻辑推理能力。
(三)情感、态度与价值观:在探索活动中,增强发现问题、解决问题的意识和养成合作交流的习惯.
教学重难点、关键
重点:n°的圆心角所对的弧长L=,扇形面积S扇=及其它们的应用.
2.难点:两个公式的应用.
3.关键:由圆的周长和面积迁移到弧长和扇形面积公式的过程.
教具、学具准备
小黑板、圆规、直尺、量角器、纸板.
教学过程
一、回顾复习
圆的周长公式:C=2πr.
圆的面积公式:S=πr2.
这里的π=30141592……,是个无理数,叫做圆周率。
情境引入
如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗?
新知探究
1、上面求的是的圆心角900所对的弧长,若圆心角为n0,如何计算它所对的弧长呢?
思考:请同学们计算半径为
r,圆心角分别为1800、900、450、n0所对的弧长。
结论:如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为:
练一练:已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度。
解:
答:此圆弧的长度为
如图,由组成圆心角的两条半径和圆心角所对的弧所围成
的图形叫扇形.
怎样计算圆心角是n0的扇形面积?
结论:如果扇形面积为s,圆心角度数为n,圆半径是r,那么扇形面积计算公式为
所以
举例应用
例1
一滑轮起重机装置(如图),滑轮的半径r=10cm,当重物上升15.7cm时,滑轮的一条半径OA绕轴心O逆时针方向旋转多少度?(假设绳索与滑轮之间没有滑动,π取3.14)
解:设半径OA绕轴心O逆时针方向旋转的度数为n°。
n≈90o
因而,旋转的角度约为90°.
例2
如图,圆心角为60°的扇形的半径为10厘米,求这个扇形的面积和周长.(π≈3.14)
解:因为n=60°,r=10厘米,所以扇形面积为
扇形的周长为
随堂练习
1.如果扇形的圆心角是230°,那么这个扇形的面积等于这个扇形所在圆的面积的(
)
2.扇形的面积是它所在圆的面积的
,这个扇形的圆心角的度数是_________°.
3.扇形的面积是S,它的半径是r,这个扇形的弧长是(
)
4.已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形=____.
5.已知扇形面积为____,圆心角为60°,则这个扇形的半径R=____.
6.已知半径为2cm的扇形,其弧长为_________
,则这个扇形的面积是_________.
7.如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为120°,OC长为8cm,CA长为12cm,则贴纸部分的面积为(
)
小结
(一
)
弧长的计算公式
(二)
扇形面积计算公式
布置作业
1.课本56面练习第1、2题。
2.预习圆柱和圆锥的侧面展开图。
