人教版九年级下册数学 28.2.2应用举例 同步习题 (word解析版)
文档属性
| 名称 | 人教版九年级下册数学 28.2.2应用举例 同步习题 (word解析版) |

|
|
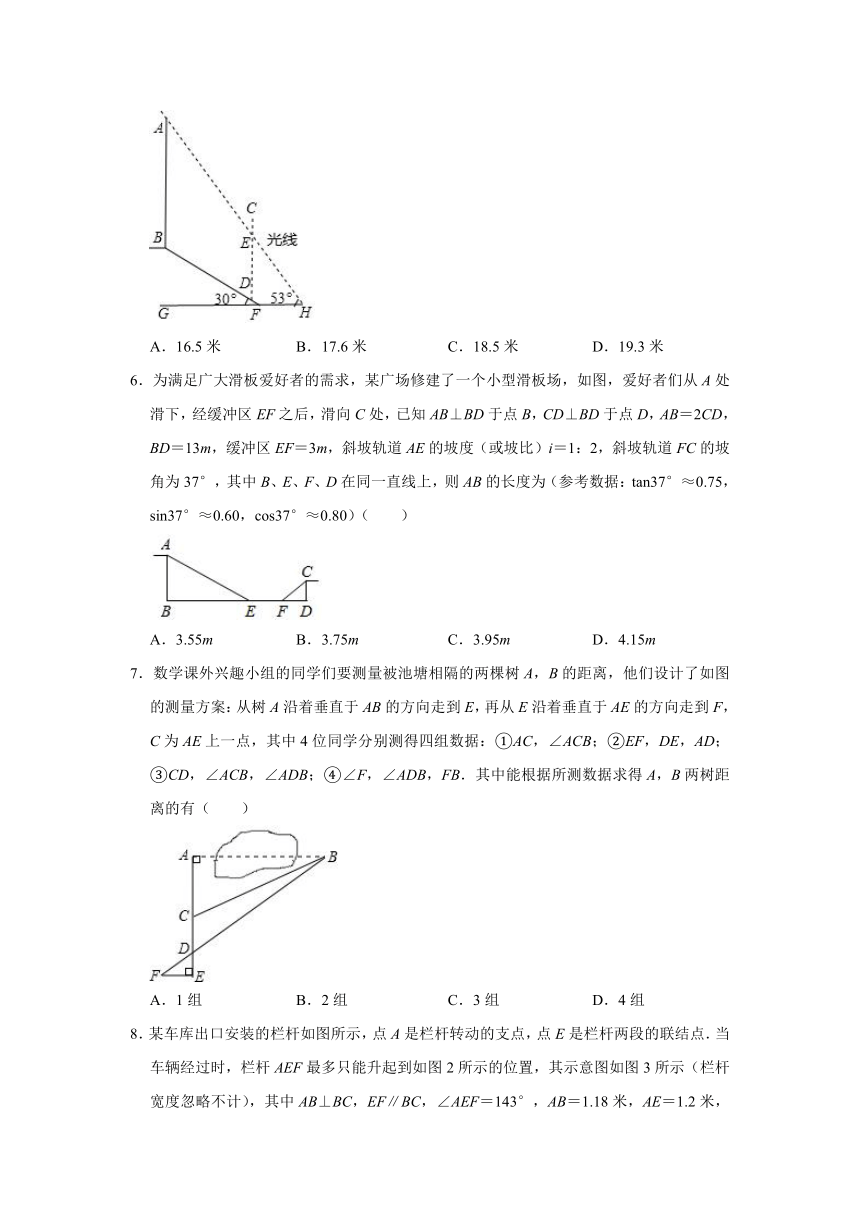
| 格式 | zip | ||
| 文件大小 | 241.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 19:23:03 | ||
图片预览


文档简介
28.2.2应用举例
同步习题
一.选择题
1.如图,为测一河两岸相对两电线杆A、B间的距离,在距A点15米处的C点(AC⊥BA)测得∠C=50°,则A、B间的距离应为( )
A.15sin50°米
B.15cos50°米
C.15tan50°米
D.米
2.为美化环境,在△ABC空地上种植售价为a元/平方米的一种草皮,已知AB=20m,AC=30m,∠A=150°,则购买草皮至少需要( )
A.450a元
B.225a元
C.150a元
D.300a元
3.某落地钟钟摆的摆长为0.5米,来回摆动的最大夹角为60°,已知在钟摆的摆动过程中,摆锤离地面的最低高度为a米,最大高度为b米,则b﹣a等于( )
A.
B.﹣
C.+
D.﹣
4.如图是一长为50米的游泳池的纵切面,该游泳池的最浅处为1.2米,最深处为2.2米,底面为斜坡,则底面的坡度为( )
A.50
B.1:50
C.3:125
D.11:250
5.如图,在坡角为30°山坡上有一座信号塔AB,其右侧有有一堵防护墙CD,测得BD的长度是10米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为12米,则信号塔AB的高度约为(参考数据:sin37°=0.60,cos37°≈0.80,tan37°=0.75,=1.73)( )
A.16.5米
B.17.6米
C.18.5米
D.19.3米
6.为满足广大滑板爱好者的需求,某广场修建了一个小型滑板场,如图,爱好者们从A处滑下,经缓冲区EF之后,滑向C处,已知AB⊥BD于点B,CD⊥BD于点D,AB=2CD,BD=13m,缓冲区EF=3m,斜坡轨道AE的坡度(或坡比)i=1:2,斜坡轨道FC的坡角为37°,其中B、E、F、D在同一直线上,则AB的长度为(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)( )
A.3.55m
B.3.75m
C.3.95m
D.4.15m
7.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中4位同学分别测得四组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB;④∠F,∠ADB,FB.其中能根据所测数据求得A,B两树距离的有( )
A.1组
B.2组
C.3组
D.4组
8.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.
B.
C.
D.
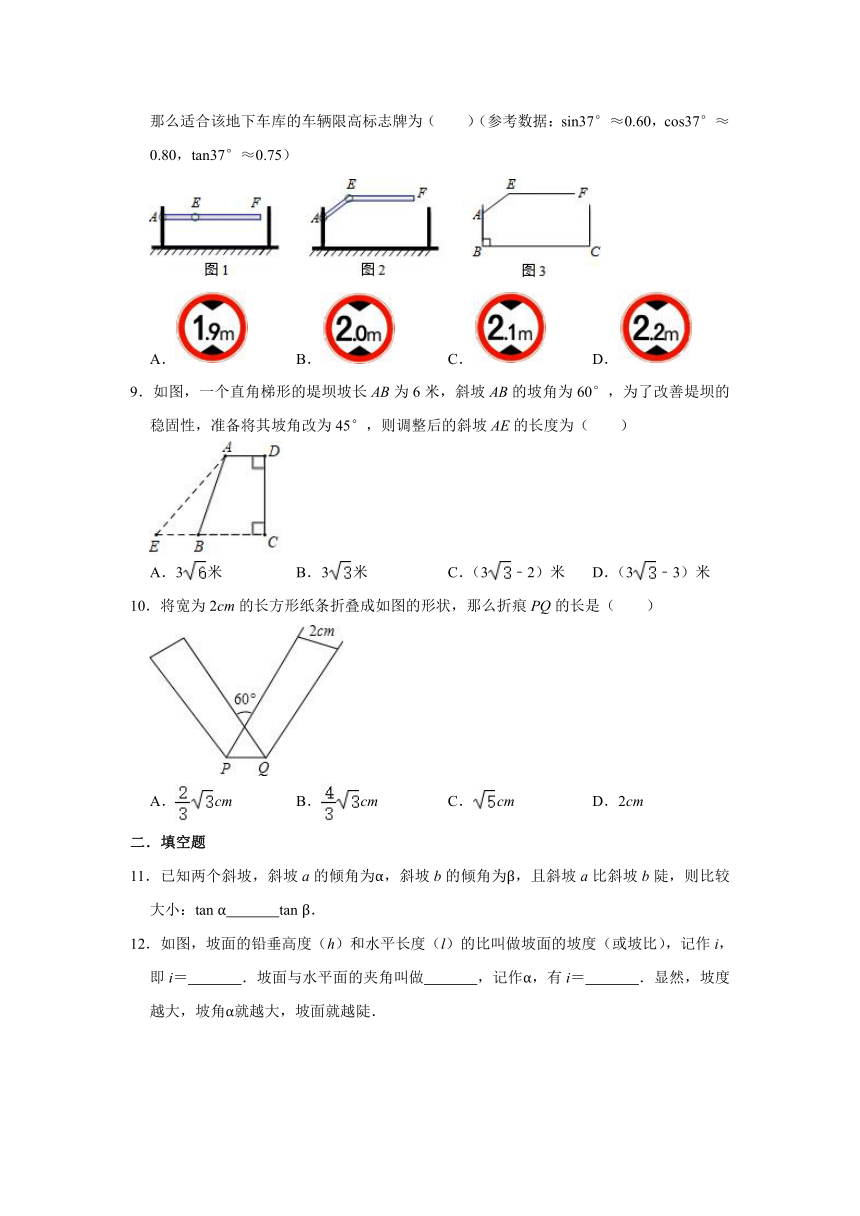
9.如图,一个直角梯形的堤坝坡长AB为6米,斜坡AB的坡角为60°,为了改善堤坝的稳固性,准备将其坡角改为45°,则调整后的斜坡AE的长度为( )
A.3米
B.3米
C.(3﹣2)米
D.(3﹣3)米
10.将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
A.cm
B.cm
C.cm
D.2cm
二.填空题
11.已知两个斜坡,斜坡a的倾角为α,斜坡b的倾角为β,且斜坡a比斜坡b陡,则比较大小:tan
α
tan
β.
12.如图,坡面的铅垂高度(h)和水平长度(l)的比叫做坡面的坡度(或坡比),记作i,即i=
.坡面与水平面的夹角叫做
,记作α,有i=
.显然,坡度越大,坡角α就越大,坡面就越陡.
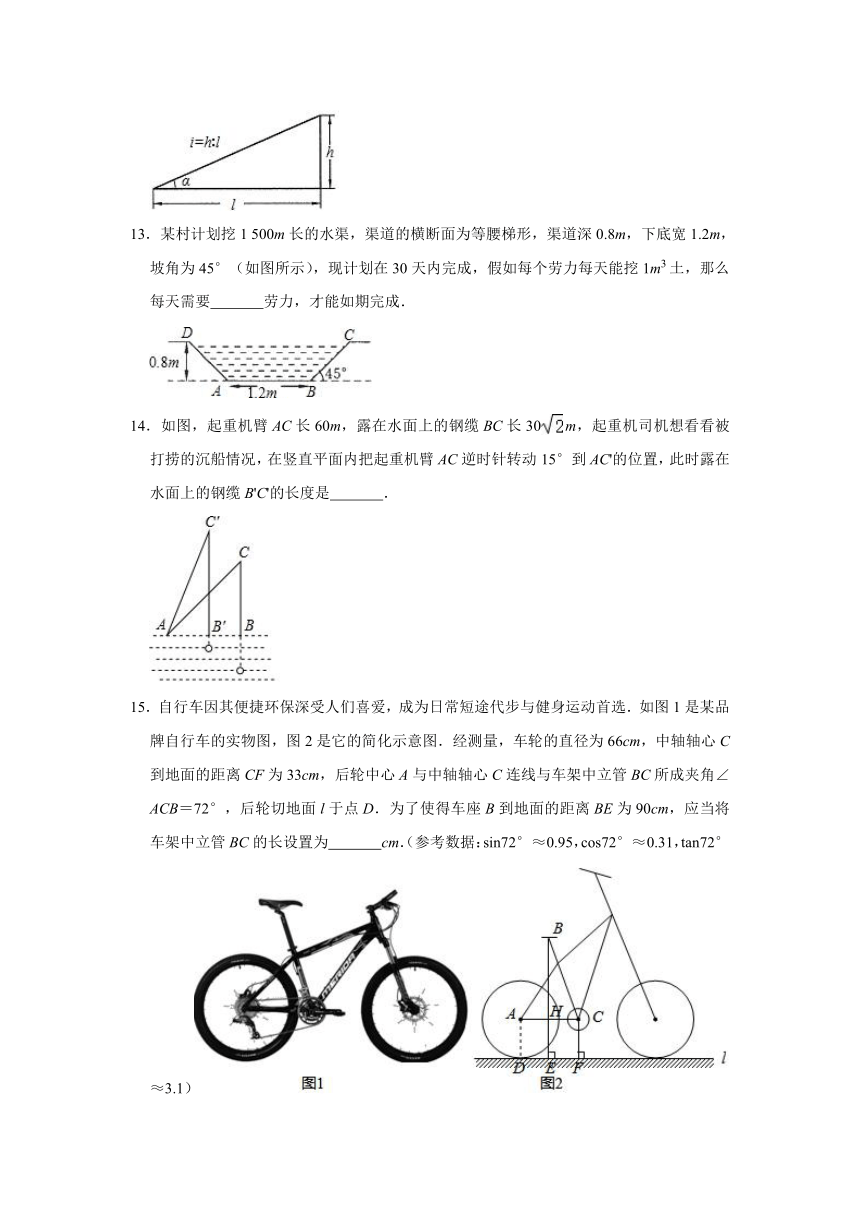
13.某村计划挖1
500m长的水渠,渠道的横断面为等腰梯形,渠道深0.8m,下底宽1.2m,坡角为45°(如图所示),现计划在30天内完成,假如每个劳力每天能挖1m3土,那么每天需要
劳力,才能如期完成.
14.如图,起重机臂AC长60m,露在水面上的钢缆BC长30m,起重机司机想看看被打捞的沉船情况,在竖直平面内把起重机臂AC逆时针转动15°到AC'的位置,此时露在水面上的钢缆B'C'的长度是
.
15.自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为66cm,中轴轴心C到地面的距离CF为33cm,后轮中心A与中轴轴心C连线与车架中立管BC所成夹角∠ACB=72°,后轮切地面l于点D.为了使得车座B到地面的距离BE为90cm,应当将车架中立管BC的长设置为
cm.(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.1)
三.解答题
16.如图是一个蔬菜种植大棚的示意图.其中,AB=3m,BC=6m,AA1=28m,∠BCD=45°,AB⊥BC,DE=1m,面ADD1A1和DCC1D1都用钢架制成并用塑料薄膜覆盖.已知墙体及其他设备的造价为3200元,钢架及塑料薄膜的平均价格为50元/m2,修建一个这样的蔬菜大棚总造价为多少元(精确到1元)?
17.如图,人民公园入口处原有三级台阶,每级台阶高20cm,宽30cm,为了方便残疾人,拟将台阶改为斜坡.设台阶的起点为A,斜坡的起点为C,现将斜坡BC的坡比定为1:8.求AC和BC的长.
18.如图1,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD,并与棱BB'交于点Q.此时液体的形状为直三棱柱,其三视图及尺寸如图2所示请解决下列问题:
(1)CQ与BE的位置关系是
,BQ的长是
dm:
(2)求液体的体积;(提示:直棱柱体积=底面积×高)
(3)若容器底部的倾斜角∠CBE=α,求α的度数.(参考数据:sin49°=cos41°=,tan37°=)
参考答案
一.选择题
1.解:因为AC=15米,∠C=50°,在直角△ABC中tan50°=,
所以AB=15?tan50°米.
故选:C.
2.解:过C点作BA的垂线交BA的延长线于点D,
∴∠DAC=30°.
又∵AC=30m,
∴DC=15m,
∴S△ABC=AB?CD=×20×15=150(m2),
∴购买草皮需要150a元.
故选:C.
3.解:如上图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,
所以AD=b,CE=a,CF=b﹣a,∠AOB=60°,
∴∠AOC=30°.
作AF⊥OC与F,
则在△AOC中,OF=OAcos30°=,
∴CF=b﹣a=OC﹣OF=﹣,
∵摆长为0.5米,∴OA=0.5米,
∴OF=,
∴b﹣a=0.5﹣,
∴b﹣a=(﹣)米.
故选:D.
4.解:因为水平距离为50米,则底面的坡度为=1:50.
故选:B.
5.解:如图,过点D作DM⊥AB交AB的延长线于M,交AH于N.
在Rt△DBM中,∵∠BDM=30°,BD=10米,
∴BM=BD=5(米),DM=BM=5=(米),
在Rt△DEN中,∵∠DNE=53°,DE=12米,
∴∠DEN=90°﹣∠DNE=90°﹣53°=37°,
∴DN=DE?tan37°=12?tan37°=12×0.75=9米,
在Rt△AMN中,AM==≈23.5(米),
∴AB=AM﹣BM=23.5﹣5=18.5(米),
故选:C.
6.解:∵AB=2CD,
∴设DC=x,则AB=2x,
∵tan37°≈0.75,
∴==0.75,
则DF=x,
∵斜坡轨道AE的坡度(或坡比)i=1:2,
∴BE=2AB=4x,
故BD﹣EF=BE+FD=13﹣3=4x+x,
解得:x=,
故AB=2×==3.75(m).
故选:B.
7.解:此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中设AC=x,AD=CD+x,AB=,AB=;
因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB.
第④组中,在直角△DEF中已知条件中没有边,无法求得DF或EF或DE的长度,从而无法求得AB的长度;、
故选:C.
8.解:如图,延长BA、FE,交于点D,
∵AB⊥BC,EF∥BC,
∴BD⊥DF,即∠ADE=90°,
∵∠AEF=143°,
∴∠AED=37°,
在Rt△ADE中,
∵sin∠AED=,AE=1.2米,
∴AD=AEsin∠AED=1.2×sin37°≈0.72(米),
则BD=AB+AD=1.18+0.72=1.9(米),
故选:A.
9.解:作AH⊥BC于H,
在Rt△ABH中,sin∠ABH=,cos∠ABH=,
则AH=AB?sin∠ABH=6×=3,
∵∠E=45°,
∴AE=AH=×3=3,
故选:A.
10.解:如图,作PM⊥OQ,QN⊥OP,垂足为M、N,
∵长方形纸条的宽为2cm,
∴PM=QN=2cm,
∴OQ=OP,
∵∠POQ=60°,
∴△POQ是等边三角形,
在Rt△PQN中,PQ===cm.
故选:B.
二.填空题
11.解:∵斜坡a的倾角为α,斜坡b的倾角为β,且斜坡a比斜坡b陡,
∴α>β,
则tanα>tanβ.
故答案为:tanα>tanβ.
12.解:坡度=铅垂高度:水平长度,∴i=;
坡面与水平面的夹角叫做坡角;坡度也可以看作坡角的正切值,∴i=tanα.
13.解:作AH⊥DC于H,BG⊥DC于G.
∵CD∥AB,
∴∠GCB=45°.
又∵BG⊥CD,
∴BGC为等腰三角形.
∴GC=BG=0.8m.
同理,DH=AH=0.8m.
又∵AB∥CD,
∴四边形ABGH为矩形,HG=AB=1.2m.
∴CD=CG+GH+HD
=0.8+1.2+0.8=2.8(m).
∴水渠横截面积
S=(2.8+1.2)×0.8=1.6(m2).
∴修整条水渠挖的土数量为
S?1500=1.6×1500=2400(m3).
每天需挖土数量为2400÷30=80(m3).
每天安排劳力为80÷1=80(名).
即每天安排80名劳力才能如期完工.
故填80.
14.解:∵sin∠CAB===,
∴∠CAB=45°.
∵∠C′AC=15°,
∴∠C′AB′=60°.
∴sin60°==,
解得:B′C′=30.
故答案为30.
15.解:由题意可得:HE=FC=33cm,
故BH=BE﹣HE=90﹣33=57(cm),
则sin72°==≈0.95,
解得:BC≈60(cm).
故答案为:60.
三.解答题
16.解:由题意可知,DE⊥BC,DF⊥AB,四边形ADD1A1和DCC1D1都是矩形,且AA1=DD1=CC1=28m,
∵∠BCD=45°,
∴DE=CE=1m,
∴DC=m.
则四边形DCC1D1的面积为:DC×CC1=×28=28m2.
∵DE⊥BC,DF⊥AB,AB⊥BC,
∴四边形BFDE是矩形.
∴BF=DE=1m,DF=BE=BC﹣CE=6﹣1=5m,
∴AF=AB﹣BF=3﹣1=2m.
∵AF=2m,DF=5m,DF⊥AB,
∴AD=.
则四边形ADD1A1的面积为:AD×AA1=×28=28m2.
∴用钢材制成的两个面的面积为(28+28)m2.
∵墙体积其他设备的造价为3200元,钢架及塑料薄膜的平均价格为50元/m2,
∴蔬菜大棚的总费用为:3200+50×(28+28)≈12719元.
∴修建一个这样的蔬菜大棚总造价约为12719元.
17.解:设AC=x,则根据题意可知:
60:(x+60)=1:8,
解得x=420,
即AC=420cm,
根据勾股定理,得
BC==60cm.
答:AC和BC的长为420cm,60cm.
18.解:(1)CQ∥BE,BQ==3dm.
故答案为:平行,3.
(2)V液=×3×4×4=24(dm3).
(3)∵CQ∥BE,
∴∠CBE=∠BCQ,
∵在Rt△BCQ中,tan∠BCQ==,
∴∠BCQ=37°,
∴α=∠BCQ=37°.
同步习题
一.选择题
1.如图,为测一河两岸相对两电线杆A、B间的距离,在距A点15米处的C点(AC⊥BA)测得∠C=50°,则A、B间的距离应为( )
A.15sin50°米
B.15cos50°米
C.15tan50°米
D.米
2.为美化环境,在△ABC空地上种植售价为a元/平方米的一种草皮,已知AB=20m,AC=30m,∠A=150°,则购买草皮至少需要( )
A.450a元
B.225a元
C.150a元
D.300a元
3.某落地钟钟摆的摆长为0.5米,来回摆动的最大夹角为60°,已知在钟摆的摆动过程中,摆锤离地面的最低高度为a米,最大高度为b米,则b﹣a等于( )
A.
B.﹣
C.+
D.﹣
4.如图是一长为50米的游泳池的纵切面,该游泳池的最浅处为1.2米,最深处为2.2米,底面为斜坡,则底面的坡度为( )
A.50
B.1:50
C.3:125
D.11:250
5.如图,在坡角为30°山坡上有一座信号塔AB,其右侧有有一堵防护墙CD,测得BD的长度是10米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为12米,则信号塔AB的高度约为(参考数据:sin37°=0.60,cos37°≈0.80,tan37°=0.75,=1.73)( )
A.16.5米
B.17.6米
C.18.5米
D.19.3米
6.为满足广大滑板爱好者的需求,某广场修建了一个小型滑板场,如图,爱好者们从A处滑下,经缓冲区EF之后,滑向C处,已知AB⊥BD于点B,CD⊥BD于点D,AB=2CD,BD=13m,缓冲区EF=3m,斜坡轨道AE的坡度(或坡比)i=1:2,斜坡轨道FC的坡角为37°,其中B、E、F、D在同一直线上,则AB的长度为(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)( )
A.3.55m
B.3.75m
C.3.95m
D.4.15m
7.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中4位同学分别测得四组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB;④∠F,∠ADB,FB.其中能根据所测数据求得A,B两树距离的有( )
A.1组
B.2组
C.3组
D.4组
8.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.
B.
C.
D.
9.如图,一个直角梯形的堤坝坡长AB为6米,斜坡AB的坡角为60°,为了改善堤坝的稳固性,准备将其坡角改为45°,则调整后的斜坡AE的长度为( )
A.3米
B.3米
C.(3﹣2)米
D.(3﹣3)米
10.将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
A.cm
B.cm
C.cm
D.2cm
二.填空题
11.已知两个斜坡,斜坡a的倾角为α,斜坡b的倾角为β,且斜坡a比斜坡b陡,则比较大小:tan
α
tan
β.
12.如图,坡面的铅垂高度(h)和水平长度(l)的比叫做坡面的坡度(或坡比),记作i,即i=
.坡面与水平面的夹角叫做
,记作α,有i=
.显然,坡度越大,坡角α就越大,坡面就越陡.
13.某村计划挖1
500m长的水渠,渠道的横断面为等腰梯形,渠道深0.8m,下底宽1.2m,坡角为45°(如图所示),现计划在30天内完成,假如每个劳力每天能挖1m3土,那么每天需要
劳力,才能如期完成.
14.如图,起重机臂AC长60m,露在水面上的钢缆BC长30m,起重机司机想看看被打捞的沉船情况,在竖直平面内把起重机臂AC逆时针转动15°到AC'的位置,此时露在水面上的钢缆B'C'的长度是
.
15.自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为66cm,中轴轴心C到地面的距离CF为33cm,后轮中心A与中轴轴心C连线与车架中立管BC所成夹角∠ACB=72°,后轮切地面l于点D.为了使得车座B到地面的距离BE为90cm,应当将车架中立管BC的长设置为
cm.(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.1)
三.解答题
16.如图是一个蔬菜种植大棚的示意图.其中,AB=3m,BC=6m,AA1=28m,∠BCD=45°,AB⊥BC,DE=1m,面ADD1A1和DCC1D1都用钢架制成并用塑料薄膜覆盖.已知墙体及其他设备的造价为3200元,钢架及塑料薄膜的平均价格为50元/m2,修建一个这样的蔬菜大棚总造价为多少元(精确到1元)?
17.如图,人民公园入口处原有三级台阶,每级台阶高20cm,宽30cm,为了方便残疾人,拟将台阶改为斜坡.设台阶的起点为A,斜坡的起点为C,现将斜坡BC的坡比定为1:8.求AC和BC的长.
18.如图1,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD,并与棱BB'交于点Q.此时液体的形状为直三棱柱,其三视图及尺寸如图2所示请解决下列问题:
(1)CQ与BE的位置关系是
,BQ的长是
dm:
(2)求液体的体积;(提示:直棱柱体积=底面积×高)
(3)若容器底部的倾斜角∠CBE=α,求α的度数.(参考数据:sin49°=cos41°=,tan37°=)
参考答案
一.选择题
1.解:因为AC=15米,∠C=50°,在直角△ABC中tan50°=,
所以AB=15?tan50°米.
故选:C.
2.解:过C点作BA的垂线交BA的延长线于点D,
∴∠DAC=30°.
又∵AC=30m,
∴DC=15m,
∴S△ABC=AB?CD=×20×15=150(m2),
∴购买草皮需要150a元.
故选:C.
3.解:如上图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,
所以AD=b,CE=a,CF=b﹣a,∠AOB=60°,
∴∠AOC=30°.
作AF⊥OC与F,
则在△AOC中,OF=OAcos30°=,
∴CF=b﹣a=OC﹣OF=﹣,
∵摆长为0.5米,∴OA=0.5米,
∴OF=,
∴b﹣a=0.5﹣,
∴b﹣a=(﹣)米.
故选:D.
4.解:因为水平距离为50米,则底面的坡度为=1:50.
故选:B.
5.解:如图,过点D作DM⊥AB交AB的延长线于M,交AH于N.
在Rt△DBM中,∵∠BDM=30°,BD=10米,
∴BM=BD=5(米),DM=BM=5=(米),
在Rt△DEN中,∵∠DNE=53°,DE=12米,
∴∠DEN=90°﹣∠DNE=90°﹣53°=37°,
∴DN=DE?tan37°=12?tan37°=12×0.75=9米,
在Rt△AMN中,AM==≈23.5(米),
∴AB=AM﹣BM=23.5﹣5=18.5(米),
故选:C.
6.解:∵AB=2CD,
∴设DC=x,则AB=2x,
∵tan37°≈0.75,
∴==0.75,
则DF=x,
∵斜坡轨道AE的坡度(或坡比)i=1:2,
∴BE=2AB=4x,
故BD﹣EF=BE+FD=13﹣3=4x+x,
解得:x=,
故AB=2×==3.75(m).
故选:B.
7.解:此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中设AC=x,AD=CD+x,AB=,AB=;
因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB.
第④组中,在直角△DEF中已知条件中没有边,无法求得DF或EF或DE的长度,从而无法求得AB的长度;、
故选:C.
8.解:如图,延长BA、FE,交于点D,
∵AB⊥BC,EF∥BC,
∴BD⊥DF,即∠ADE=90°,
∵∠AEF=143°,
∴∠AED=37°,
在Rt△ADE中,
∵sin∠AED=,AE=1.2米,
∴AD=AEsin∠AED=1.2×sin37°≈0.72(米),
则BD=AB+AD=1.18+0.72=1.9(米),
故选:A.
9.解:作AH⊥BC于H,
在Rt△ABH中,sin∠ABH=,cos∠ABH=,
则AH=AB?sin∠ABH=6×=3,
∵∠E=45°,
∴AE=AH=×3=3,
故选:A.
10.解:如图,作PM⊥OQ,QN⊥OP,垂足为M、N,
∵长方形纸条的宽为2cm,
∴PM=QN=2cm,
∴OQ=OP,
∵∠POQ=60°,
∴△POQ是等边三角形,
在Rt△PQN中,PQ===cm.
故选:B.
二.填空题
11.解:∵斜坡a的倾角为α,斜坡b的倾角为β,且斜坡a比斜坡b陡,
∴α>β,
则tanα>tanβ.
故答案为:tanα>tanβ.
12.解:坡度=铅垂高度:水平长度,∴i=;
坡面与水平面的夹角叫做坡角;坡度也可以看作坡角的正切值,∴i=tanα.
13.解:作AH⊥DC于H,BG⊥DC于G.
∵CD∥AB,
∴∠GCB=45°.
又∵BG⊥CD,
∴BGC为等腰三角形.
∴GC=BG=0.8m.
同理,DH=AH=0.8m.
又∵AB∥CD,
∴四边形ABGH为矩形,HG=AB=1.2m.
∴CD=CG+GH+HD
=0.8+1.2+0.8=2.8(m).
∴水渠横截面积
S=(2.8+1.2)×0.8=1.6(m2).
∴修整条水渠挖的土数量为
S?1500=1.6×1500=2400(m3).
每天需挖土数量为2400÷30=80(m3).
每天安排劳力为80÷1=80(名).
即每天安排80名劳力才能如期完工.
故填80.
14.解:∵sin∠CAB===,
∴∠CAB=45°.
∵∠C′AC=15°,
∴∠C′AB′=60°.
∴sin60°==,
解得:B′C′=30.
故答案为30.
15.解:由题意可得:HE=FC=33cm,
故BH=BE﹣HE=90﹣33=57(cm),
则sin72°==≈0.95,
解得:BC≈60(cm).
故答案为:60.
三.解答题
16.解:由题意可知,DE⊥BC,DF⊥AB,四边形ADD1A1和DCC1D1都是矩形,且AA1=DD1=CC1=28m,
∵∠BCD=45°,
∴DE=CE=1m,
∴DC=m.
则四边形DCC1D1的面积为:DC×CC1=×28=28m2.
∵DE⊥BC,DF⊥AB,AB⊥BC,
∴四边形BFDE是矩形.
∴BF=DE=1m,DF=BE=BC﹣CE=6﹣1=5m,
∴AF=AB﹣BF=3﹣1=2m.
∵AF=2m,DF=5m,DF⊥AB,
∴AD=.
则四边形ADD1A1的面积为:AD×AA1=×28=28m2.
∴用钢材制成的两个面的面积为(28+28)m2.
∵墙体积其他设备的造价为3200元,钢架及塑料薄膜的平均价格为50元/m2,
∴蔬菜大棚的总费用为:3200+50×(28+28)≈12719元.
∴修建一个这样的蔬菜大棚总造价约为12719元.
17.解:设AC=x,则根据题意可知:
60:(x+60)=1:8,
解得x=420,
即AC=420cm,
根据勾股定理,得
BC==60cm.
答:AC和BC的长为420cm,60cm.
18.解:(1)CQ∥BE,BQ==3dm.
故答案为:平行,3.
(2)V液=×3×4×4=24(dm3).
(3)∵CQ∥BE,
∴∠CBE=∠BCQ,
∵在Rt△BCQ中,tan∠BCQ==,
∴∠BCQ=37°,
∴α=∠BCQ=37°.
