五年级下册数学课件最大公因数青岛版 (共30张)
文档属性
| 名称 | 五年级下册数学课件最大公因数青岛版 (共30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
最大公因数
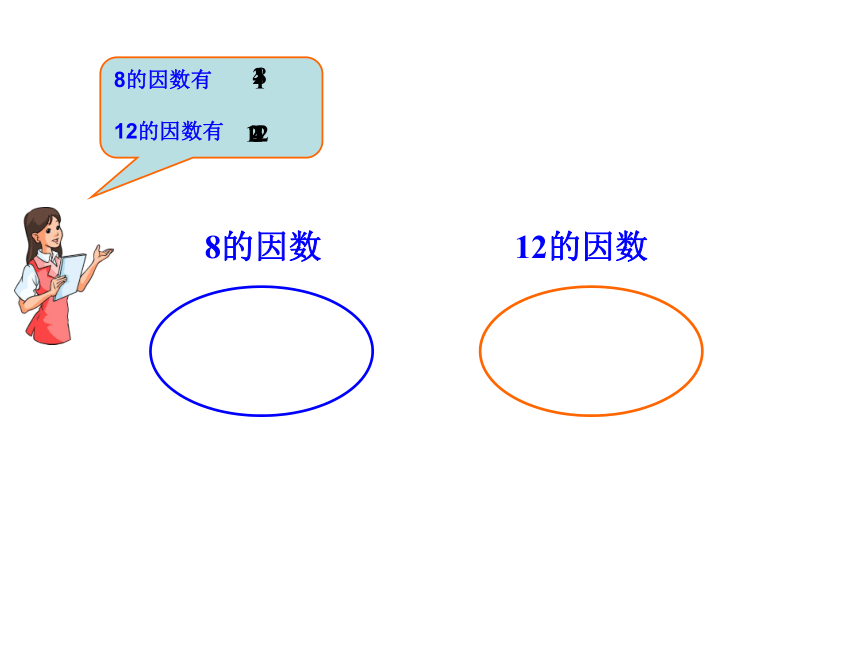
1、8和12公有的因数是哪几个?公有的最大因数是多少?
8的因数
12的因数
6
8的因数有
12的因数有
1
3
4
12
2
4
8
1
2
8
的因数
12
的因数
8,
3,6,12
1,2,4
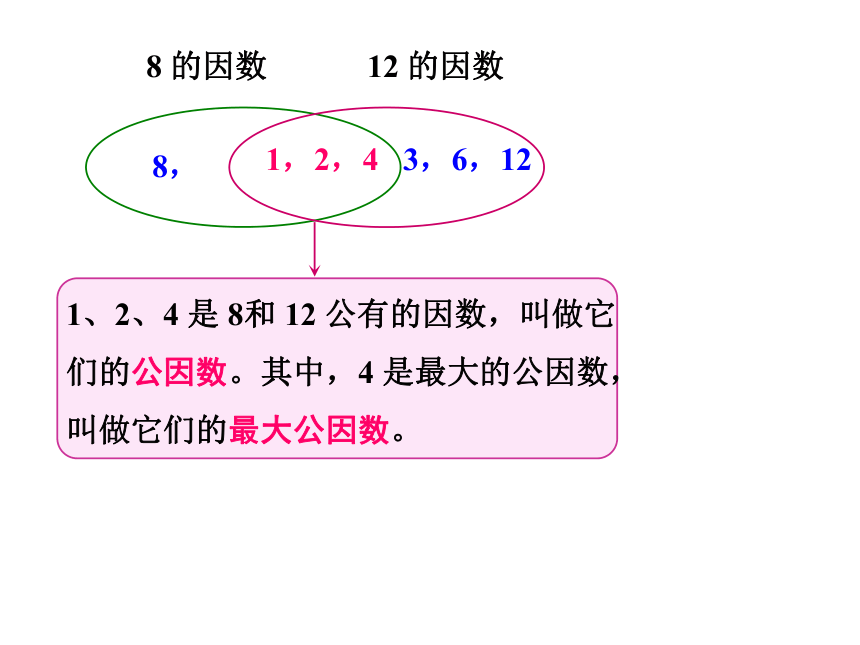
1、2、4
是
8和
12
公有的因数,叫做它们的公因数。其中,4
是最大的公因数,叫做它们的最大公因数。
怎样求
18
和
27
的最大公因数。
2
观察一下,两个数的公因数和它们的最大公因数之间有什么关系?
所有的公因数都是最大公因数的因数,最大公因数是它们的倍数。
18和27的公因
数
1,3,9
中,9
最大。
8和12的公因数是1、2、4
。其中,4
是最大的公因数,
1.口答填空:
16的因数是(
);
24的因数是(
);
16和24的公因数是(
);
12和18的最大公因数是(
)
。
巩固练习
2
3
4
6
18
1
9
12
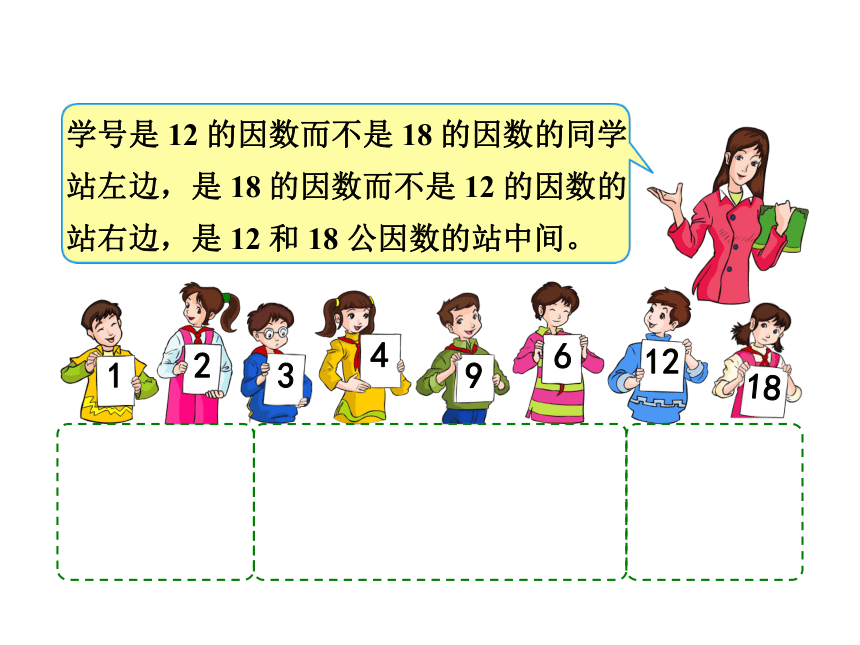
学号是
12
的因数而不是
18
的因数的同学站左边,是
18
的因数而不是
12
的因数的站右边,是
12
和
18
公因数的站中间。
我该站哪儿呢?
2
3
4
6
18
1
9
12
学号是
12
的因数而不是
18
的因数的同学站左边,是
18
的因数而不是
12
的因数的站右边,是
12
和
18
公因数的站中间。
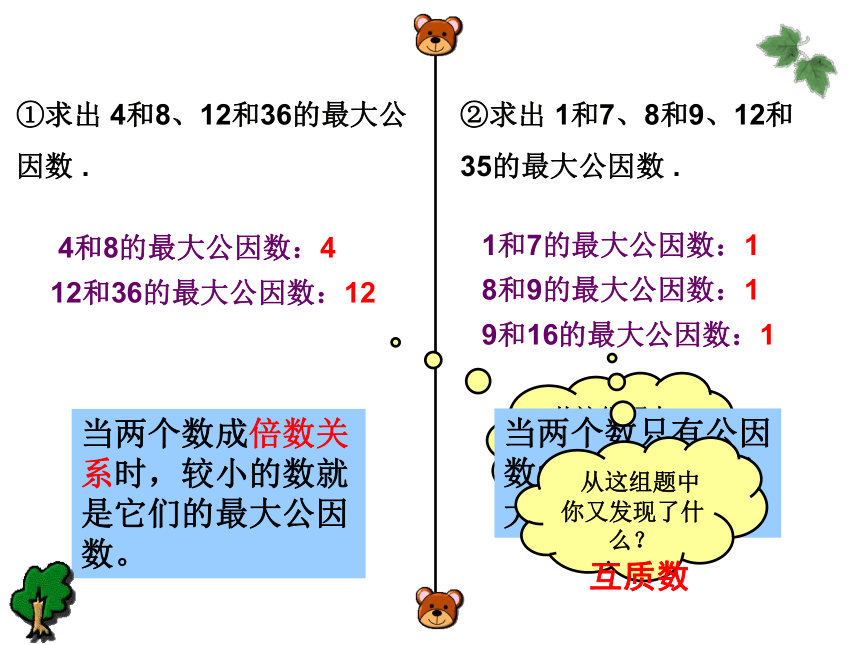
②求出
1和7、8和9、12和35的最大公因数
.
①求出
4和8、12和36的最大公因数
.
4和8的最大公因数:4
12和36的最大公因数:12
1和7的最大公因数:1
8和9的最大公因数:1
9和16的最大公因数:1
从这组题中你发现了什么?
当两个数成倍数关系时,较小的数就是它们的最大公因数。
当两个数只有公因数1时,它们的最大公因数也是1。
从这组题中你又发现了什么?
互质数
1.
填空。
(1)
10
和
15
的公因数有
_____________。
(2)
14
和
49
的公因数有
_____________。
1,5
1,7
2.
找出下面每组数的最大公因数。
6
和
9
15
和
12
42
和
54
30
和
45
5
和
9
34
和
17
16
和
48
15
和
16
3
3
6
15
1
17
16
1
3.
选出正确答案的编号填在横线上。
(1)
9
和
16
的最大公因数是______。
A.
1
B.
3
C.
4
D.
9
(2)
16
和
48
的最大公因数是______。
A.
4
B.
6
C.
8
D.
16
(3)
甲数是乙数的倍数,甲、乙两数的最大公因
数是______。
A.
1
B.
甲数
C.
乙数
D.
甲、乙两数的积
A
D
C
4.
写出下列各分数分子和分母的最大公因数。
(
)
7
9
8
36
(
)
18
72
(
)
9
15
(
)
1
4
18
3
5
3
6
12
36
5.
在相应的(
)里写出相邻阶梯上两个数的最大
公因数。
72
10
(
)
15
(
)
18
(
)
24
(
)
36
(
)
6.
按要求写出两个数,使它们的最大公因数是
1。
(1)
两个数都是质数:
____
和
____。
(2)
两个数都是合数:
____
和
____。
(3)
一个质数一个合数:
____
和
____。
2
5
4
9
13
8
如果要用边长是整分米数的正方形地砖把贮藏
室的地面铺满(使用的地砖都是整块)。可以选择边
长是几分米的地砖?
边长最大是几分米?
1
最大公因数
我们家贮藏室
长
16
dm,宽
12
dm。
可以在长方形纸上画一画,看看能画出多少个正方形。
可以用正方形
纸片摆一摆。
用边长是
3
dm
的地砖不行啊。
用边长
1dm
的方砖,可以铺满,都是整块。
12dm
16dm
用边长
2dm
的方砖,可以铺满,都是整块。
12dm
16dm
用边长
4dm
的方砖,可以铺满,都是整块。
12dm
16dm
16的因数
12的因数
要使所用的正方形地砖都是整块的,地砖的边长必须既是
16
的因数,又是
12
的因数。
1,2,3,4,6,12
1,2,4,8,16
16的因数
12的因数
16
6
12
3
8
1
2
4
1、2、4是16和12公有的因数,叫做它们的公因数。
其中,4是最大的公因数叫做它们的最大公因数。
地砖边长可以是1dm、2dm、4dm,最大是4dm。
要使所用的正方形地砖都是整块的,地砖的边长必须既是
16
的因数,又是
12
的因数。
(如图)有一块长方体木块,长7dm,宽5dm,高4.5dm。如果把它锯成同样大小的小正方体木块,最大可以锯成棱长是多少的小方块而又不浪费木料?
7dm
5dm
4.5dm
70、50和45的最大公因数是5,
所以正方体的棱长是5cm。
公因数只有
1
的两个数,叫做互质数。例如,
5
和
7
是互质数,7
和
9
也是互质数。
想一想:互质的两个数必须都是质数吗?
请你举出两个合数互质的例子来。
4
和
9,8
和
15。
互质数的几种特殊情况
1、相邻的两个自然数(0除外)。
3、两个不相同的质数。
6、1和任何一个自然数(0除外)。
4、小的数是质数,大的数不是它的
倍数的两个数。
2、相邻的两个奇数。
5、大的数是质数的两个数。
7、2和任何奇数。
7.
有一张长方形纸,长
70
cm,宽
50
cm。如果要
剪成若干同样大小的正方形而没有剩余,剪出的
小正方形的边长最大是几厘米?
10
厘米。
8.
男、女生分别排队,要使每排的人数相同,每排
最多有多少人?
这时男、女生分别有几排?
女生有
36
人。
男生有
48
人。
48
和
36
的最大公因数是
12。
48÷12
=
4
(排)
36÷12
=
3
(排)
答:
每排最多有
12
人,这时男生有
4
排,女生有
3
排。
9.
小巧匠。
12、16
和
44
的最大公因数是
4
。
答:
每根小棒最长是
4
厘米。
12
cm
16
cm
44
cm
要把它们截成同样长的小棒,不能有剩余,每根小棒最长是多少厘米?
最大公因数
1、8和12公有的因数是哪几个?公有的最大因数是多少?
8的因数
12的因数
6
8的因数有
12的因数有
1
3
4
12
2
4
8
1
2
8
的因数
12
的因数
8,
3,6,12
1,2,4
1、2、4
是
8和
12
公有的因数,叫做它们的公因数。其中,4
是最大的公因数,叫做它们的最大公因数。
怎样求
18
和
27
的最大公因数。
2
观察一下,两个数的公因数和它们的最大公因数之间有什么关系?
所有的公因数都是最大公因数的因数,最大公因数是它们的倍数。
18和27的公因
数
1,3,9
中,9
最大。
8和12的公因数是1、2、4
。其中,4
是最大的公因数,
1.口答填空:
16的因数是(
);
24的因数是(
);
16和24的公因数是(
);
12和18的最大公因数是(
)
。
巩固练习
2
3
4
6
18
1
9
12
学号是
12
的因数而不是
18
的因数的同学站左边,是
18
的因数而不是
12
的因数的站右边,是
12
和
18
公因数的站中间。
我该站哪儿呢?
2
3
4
6
18
1
9
12
学号是
12
的因数而不是
18
的因数的同学站左边,是
18
的因数而不是
12
的因数的站右边,是
12
和
18
公因数的站中间。
②求出
1和7、8和9、12和35的最大公因数
.
①求出
4和8、12和36的最大公因数
.
4和8的最大公因数:4
12和36的最大公因数:12
1和7的最大公因数:1
8和9的最大公因数:1
9和16的最大公因数:1
从这组题中你发现了什么?
当两个数成倍数关系时,较小的数就是它们的最大公因数。
当两个数只有公因数1时,它们的最大公因数也是1。
从这组题中你又发现了什么?
互质数
1.
填空。
(1)
10
和
15
的公因数有
_____________。
(2)
14
和
49
的公因数有
_____________。
1,5
1,7
2.
找出下面每组数的最大公因数。
6
和
9
15
和
12
42
和
54
30
和
45
5
和
9
34
和
17
16
和
48
15
和
16
3
3
6
15
1
17
16
1
3.
选出正确答案的编号填在横线上。
(1)
9
和
16
的最大公因数是______。
A.
1
B.
3
C.
4
D.
9
(2)
16
和
48
的最大公因数是______。
A.
4
B.
6
C.
8
D.
16
(3)
甲数是乙数的倍数,甲、乙两数的最大公因
数是______。
A.
1
B.
甲数
C.
乙数
D.
甲、乙两数的积
A
D
C
4.
写出下列各分数分子和分母的最大公因数。
(
)
7
9
8
36
(
)
18
72
(
)
9
15
(
)
1
4
18
3
5
3
6
12
36
5.
在相应的(
)里写出相邻阶梯上两个数的最大
公因数。
72
10
(
)
15
(
)
18
(
)
24
(
)
36
(
)
6.
按要求写出两个数,使它们的最大公因数是
1。
(1)
两个数都是质数:
____
和
____。
(2)
两个数都是合数:
____
和
____。
(3)
一个质数一个合数:
____
和
____。
2
5
4
9
13
8
如果要用边长是整分米数的正方形地砖把贮藏
室的地面铺满(使用的地砖都是整块)。可以选择边
长是几分米的地砖?
边长最大是几分米?
1
最大公因数
我们家贮藏室
长
16
dm,宽
12
dm。
可以在长方形纸上画一画,看看能画出多少个正方形。
可以用正方形
纸片摆一摆。
用边长是
3
dm
的地砖不行啊。
用边长
1dm
的方砖,可以铺满,都是整块。
12dm
16dm
用边长
2dm
的方砖,可以铺满,都是整块。
12dm
16dm
用边长
4dm
的方砖,可以铺满,都是整块。
12dm
16dm
16的因数
12的因数
要使所用的正方形地砖都是整块的,地砖的边长必须既是
16
的因数,又是
12
的因数。
1,2,3,4,6,12
1,2,4,8,16
16的因数
12的因数
16
6
12
3
8
1
2
4
1、2、4是16和12公有的因数,叫做它们的公因数。
其中,4是最大的公因数叫做它们的最大公因数。
地砖边长可以是1dm、2dm、4dm,最大是4dm。
要使所用的正方形地砖都是整块的,地砖的边长必须既是
16
的因数,又是
12
的因数。
(如图)有一块长方体木块,长7dm,宽5dm,高4.5dm。如果把它锯成同样大小的小正方体木块,最大可以锯成棱长是多少的小方块而又不浪费木料?
7dm
5dm
4.5dm
70、50和45的最大公因数是5,
所以正方体的棱长是5cm。
公因数只有
1
的两个数,叫做互质数。例如,
5
和
7
是互质数,7
和
9
也是互质数。
想一想:互质的两个数必须都是质数吗?
请你举出两个合数互质的例子来。
4
和
9,8
和
15。
互质数的几种特殊情况
1、相邻的两个自然数(0除外)。
3、两个不相同的质数。
6、1和任何一个自然数(0除外)。
4、小的数是质数,大的数不是它的
倍数的两个数。
2、相邻的两个奇数。
5、大的数是质数的两个数。
7、2和任何奇数。
7.
有一张长方形纸,长
70
cm,宽
50
cm。如果要
剪成若干同样大小的正方形而没有剩余,剪出的
小正方形的边长最大是几厘米?
10
厘米。
8.
男、女生分别排队,要使每排的人数相同,每排
最多有多少人?
这时男、女生分别有几排?
女生有
36
人。
男生有
48
人。
48
和
36
的最大公因数是
12。
48÷12
=
4
(排)
36÷12
=
3
(排)
答:
每排最多有
12
人,这时男生有
4
排,女生有
3
排。
9.
小巧匠。
12、16
和
44
的最大公因数是
4
。
答:
每根小棒最长是
4
厘米。
12
cm
16
cm
44
cm
要把它们截成同样长的小棒,不能有剩余,每根小棒最长是多少厘米?
