3.6.2 直线和圆的位置关系 课件(共24张PPT)
文档属性
| 名称 | 3.6.2 直线和圆的位置关系 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 14:02:29 | ||
图片预览





文档简介
第6节 直线和圆的位置关系
(第2课时)
第三章 圆
2020-2021北师大版九年级数学下册
1 能判定一条直线是否为圆的切线,会过圆上一点画圆的切线
2 知道三角形的内心是三个角的平分线的交点,会作出三角形的内心,能借助三角形的内心解决实际问题
学习目标
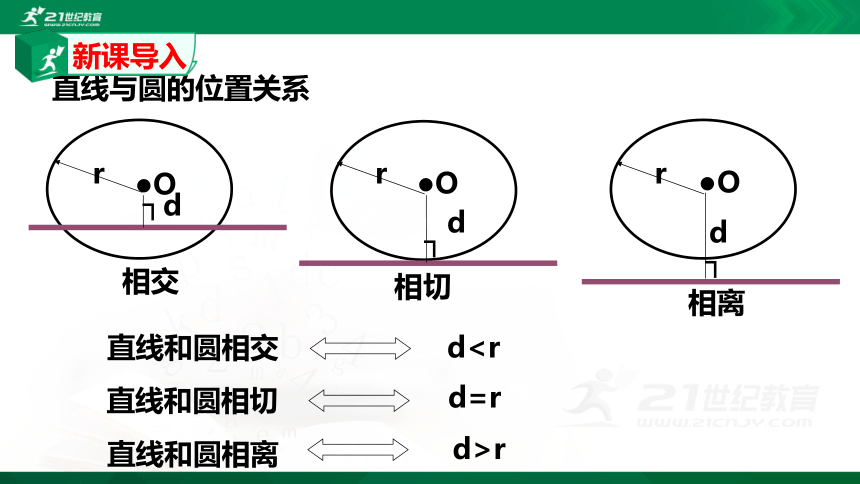
直线与圆的位置关系
直线和圆相交
d=r
d 直线和圆相切
直线和圆相离
d>r
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
新课导入
圆的切线的判定
知识点一
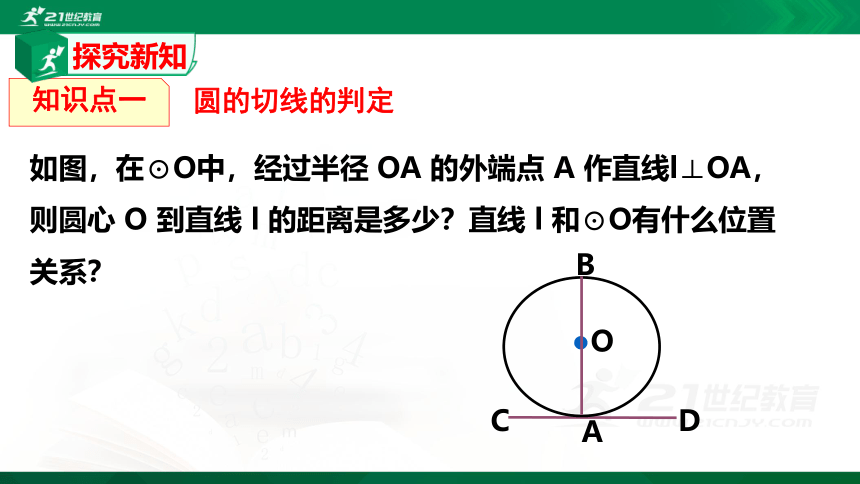
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
C
D
B
●O
A
探究新知
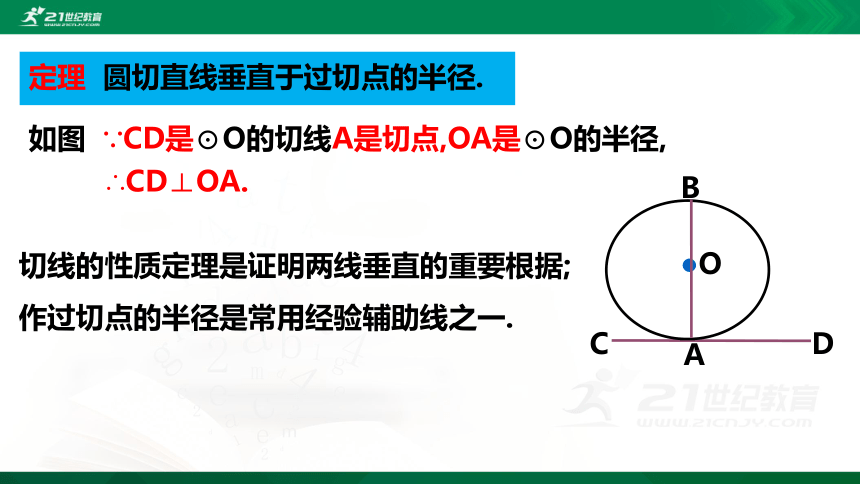
定理 圆切直线垂直于过切点的半径.
如图 ∵CD是⊙O的切线A是切点,OA是⊙O的半径,
∴CD⊥OA.
切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.
C
D
B
●O
A
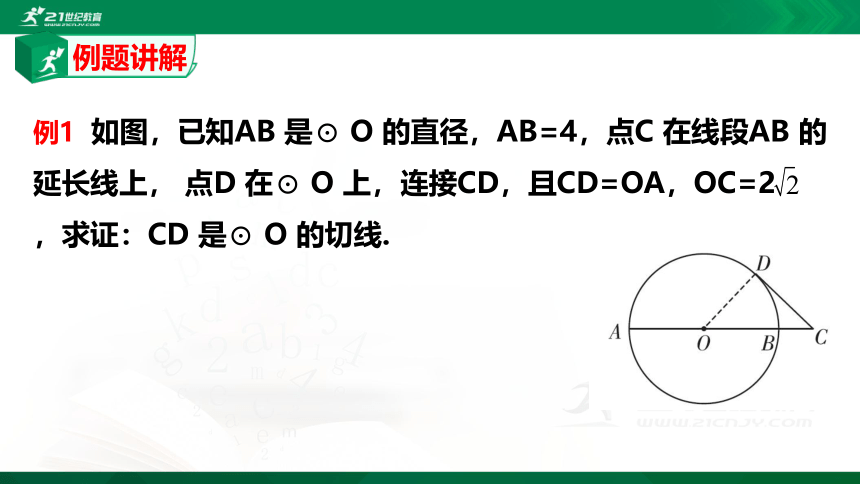
例1 如图,已知AB 是⊙ O 的直径,AB=4,点C 在线段AB 的延长线上, 点D 在⊙ O 上,连接CD,且CD=OA,OC=2 ,求证:CD 是⊙ O 的切线.
例题讲解
证明:连接OD.
由题意可知CD=OD=OA= AB=2.
∵ OC=2 ,
∴ OD2+CD2=OC2.
∴∠ ODC=90°,即OD ⊥ CD.又点D 在⊙ O 上,
∴ CD 是⊙ O 的切线.
总结:切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即经过半径的外端并且垂直这条半径的直线是圆的切线.
三角形的内切圆
知识点二
这样的圆可以作出几个?为什么?
∵ 直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等,
∴ 和△ABC三边都相切的圆可以作出一个,并且只能作一个.
A
B
C
I●
┓
E
F
作法:
1 作∠B,∠C的平分线BE和CF,交点为I,如图.
2 过I作BC的垂线,垂足为D.
3 以I为圆心,以ID为半径作⊙I.⊙I就是所求的圆.
这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
A
B
C
●
I
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形
⊙O的名称
△ABC的名称
圆心O的确定
“心”的性质
“心”的位置
△ABC的内切圆
⊙O的外切三角形
三角形三条角平分线的交点
到三角形的三条边的距离相等
一定在三角形内部
例2 已知AB为⊙O的直径,直线BC与⊙O相切于点B,过A作AD∥OC交⊙O于点D,连结CD.
求证:CD是⊙O的切线.
例题讲解
证明:连接OD,如图所示:
∵OA=OD,
∴∠ODA=∠OAD.
∵AD∥CO,
∴∠COD=∠ODA,∠COB=∠OAD.
∴∠COD=∠COB.
在△ODC和△OBC中,????????=????????∠????????????=∠????????????????????=????????
∴△ODC≌△OBC(SAS).∴∠ODC=∠OBC.
∵CB是圆O的切线且OB为半径,
∴∠CBO=90°.∴∠CDO=90°.∴OD⊥CD.
又∵CD经过半径OD的外端点D,
∴CD为圆O的切线.
?
切线的性质定理:圆的切线垂直于过切点的半径.
知识点三
四边形与圆的位置关系
知识点三
如果四边形的四条边都与一个圆相切,这圆叫做四边形的内切圆.这个四边形叫做圆的外切四边形.
我们可以证明圆外切四边的一个重要性质:
圆外切四边形两组对边的和相等.
●O
A
B
C
D
1 下列说法错误的是( )
A.三角形的内切圆与三角形的三边都相切
B.一个三角形一定有唯一一个内切圆
C.一个圆一定有唯一一个外切三角形
D.等边三角形的内切圆与外接圆是同心圆
课堂练习
2 如图,△ABC是⊙O的内接三角形,下列选项中,能使过点A的直线EF与⊙O相切于点A的条件是( )
A.∠EAB=∠C
B.∠EAB=∠BAC
C.EF⊥AC
D.AC是⊙O的直径
3 如图,AB是⊙O的直径,线段BC与⊙O的交点D是BC的中点,DE⊥AC于点E,连接AD,则下列结论中正确的个数是( )
①AD⊥BC;②∠EDA=∠B;
③OA= AC;④DE是⊙O的切线.
A.1 B.2
C.3 D.4
4 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
5 如图,以O为圆心的两个同心圆,大圆的弦AB是小圆的切线,切点为P。
求证:AP=BP。
切线的三种判定方法:
(1)定义;
(2)数量关系;
(3)位置关系(切线的判定定理):经过半径外端并且垂直于这条半径的直线是圆的切线。在切线的三种判定方法中,常用的是后两种判定方法,在判定圆的切线时,往往需要添加辅助线.
课堂小结
谢谢聆听
(第2课时)
第三章 圆
2020-2021北师大版九年级数学下册
1 能判定一条直线是否为圆的切线,会过圆上一点画圆的切线
2 知道三角形的内心是三个角的平分线的交点,会作出三角形的内心,能借助三角形的内心解决实际问题
学习目标
直线与圆的位置关系
直线和圆相交
d=r
d
直线和圆相离
d>r
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
新课导入
圆的切线的判定
知识点一
如图,在⊙O中,经过半径 OA 的外端点 A 作直线l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O有什么位置关系?
C
D
B
●O
A
探究新知
定理 圆切直线垂直于过切点的半径.
如图 ∵CD是⊙O的切线A是切点,OA是⊙O的半径,
∴CD⊥OA.
切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.
C
D
B
●O
A
例1 如图,已知AB 是⊙ O 的直径,AB=4,点C 在线段AB 的延长线上, 点D 在⊙ O 上,连接CD,且CD=OA,OC=2 ,求证:CD 是⊙ O 的切线.
例题讲解
证明:连接OD.
由题意可知CD=OD=OA= AB=2.
∵ OC=2 ,
∴ OD2+CD2=OC2.
∴∠ ODC=90°,即OD ⊥ CD.又点D 在⊙ O 上,
∴ CD 是⊙ O 的切线.
总结:切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即经过半径的外端并且垂直这条半径的直线是圆的切线.
三角形的内切圆
知识点二
这样的圆可以作出几个?为什么?
∵ 直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等,
∴ 和△ABC三边都相切的圆可以作出一个,并且只能作一个.
A
B
C
I●
┓
E
F
作法:
1 作∠B,∠C的平分线BE和CF,交点为I,如图.
2 过I作BC的垂线,垂足为D.
3 以I为圆心,以ID为半径作⊙I.⊙I就是所求的圆.
这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
A
B
C
●
I
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形
⊙O的名称
△ABC的名称
圆心O的确定
“心”的性质
“心”的位置
△ABC的内切圆
⊙O的外切三角形
三角形三条角平分线的交点
到三角形的三条边的距离相等
一定在三角形内部
例2 已知AB为⊙O的直径,直线BC与⊙O相切于点B,过A作AD∥OC交⊙O于点D,连结CD.
求证:CD是⊙O的切线.
例题讲解
证明:连接OD,如图所示:
∵OA=OD,
∴∠ODA=∠OAD.
∵AD∥CO,
∴∠COD=∠ODA,∠COB=∠OAD.
∴∠COD=∠COB.
在△ODC和△OBC中,????????=????????∠????????????=∠????????????????????=????????
∴△ODC≌△OBC(SAS).∴∠ODC=∠OBC.
∵CB是圆O的切线且OB为半径,
∴∠CBO=90°.∴∠CDO=90°.∴OD⊥CD.
又∵CD经过半径OD的外端点D,
∴CD为圆O的切线.
?
切线的性质定理:圆的切线垂直于过切点的半径.
知识点三
四边形与圆的位置关系
知识点三
如果四边形的四条边都与一个圆相切,这圆叫做四边形的内切圆.这个四边形叫做圆的外切四边形.
我们可以证明圆外切四边的一个重要性质:
圆外切四边形两组对边的和相等.
●O
A
B
C
D
1 下列说法错误的是( )
A.三角形的内切圆与三角形的三边都相切
B.一个三角形一定有唯一一个内切圆
C.一个圆一定有唯一一个外切三角形
D.等边三角形的内切圆与外接圆是同心圆
课堂练习
2 如图,△ABC是⊙O的内接三角形,下列选项中,能使过点A的直线EF与⊙O相切于点A的条件是( )
A.∠EAB=∠C
B.∠EAB=∠BAC
C.EF⊥AC
D.AC是⊙O的直径
3 如图,AB是⊙O的直径,线段BC与⊙O的交点D是BC的中点,DE⊥AC于点E,连接AD,则下列结论中正确的个数是( )
①AD⊥BC;②∠EDA=∠B;
③OA= AC;④DE是⊙O的切线.
A.1 B.2
C.3 D.4
4 如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
5 如图,以O为圆心的两个同心圆,大圆的弦AB是小圆的切线,切点为P。
求证:AP=BP。
切线的三种判定方法:
(1)定义;
(2)数量关系;
(3)位置关系(切线的判定定理):经过半径外端并且垂直于这条半径的直线是圆的切线。在切线的三种判定方法中,常用的是后两种判定方法,在判定圆的切线时,往往需要添加辅助线.
课堂小结
谢谢聆听
