3.5 确定圆的条件 课件(共20张PPT)
文档属性
| 名称 | 3.5 确定圆的条件 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览






文档简介
第5节 确定圆的条件
第三章 圆
2020-2021北师大版九年级数学下册
1 了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法;
2 了解三角形的外接圆、三角形的外心等概念.
3 经历不在同一直线上的三个点确定一个圆的探索过程,
培养学生的探索能力.
学习目标
1 过一点可以作几条直线?
2 过几点可确定一条直线?
思考:过几点可以确定一个圆呢?
新课导入
确定圆的条件
知识点一
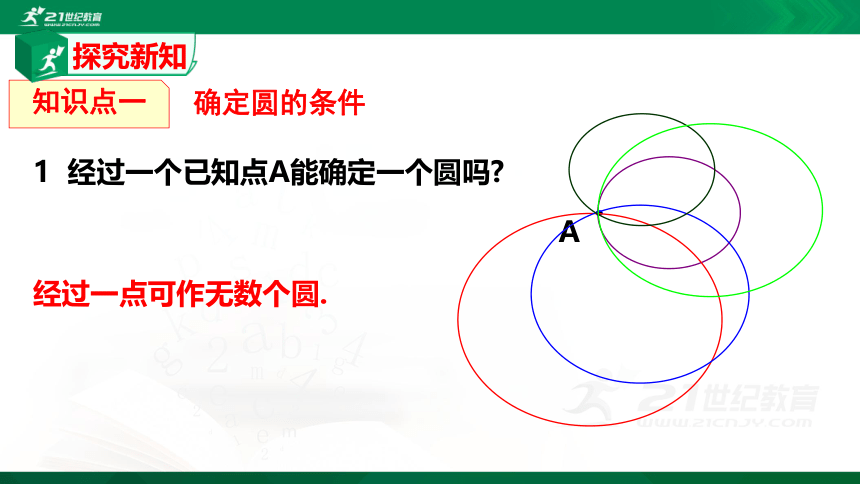
1 经过一个已知点A能确定一个圆吗?
A
经过一点可作无数个圆.
探究新知
2 经过两个已知点A,B能确定一个圆吗?
A
B
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
它们的圆心都在线段AB的垂直平分线上.
经过两个已知点A,B能作无数个圆.
如图所示,点A,B,C 在同一条直线上,点D 在直线AB 外,过这四个点中的任意三个点,能画圆的个数是( )
A.1 B.2 C.3 D.4
例1
C
例题讲解
解:过不在同一条直线上的三点确定一个圆,在点A,B,C,D 四个点中取三个点的方法有:点A,B,C;点A,B,D;点B,C,D;点A,C,D,共四组. 又因A,B,C 三点在同一条直线上,故过这四个点中的任意三个点能画圆的个数为3.
三角形的外接圆与外心
知识点二
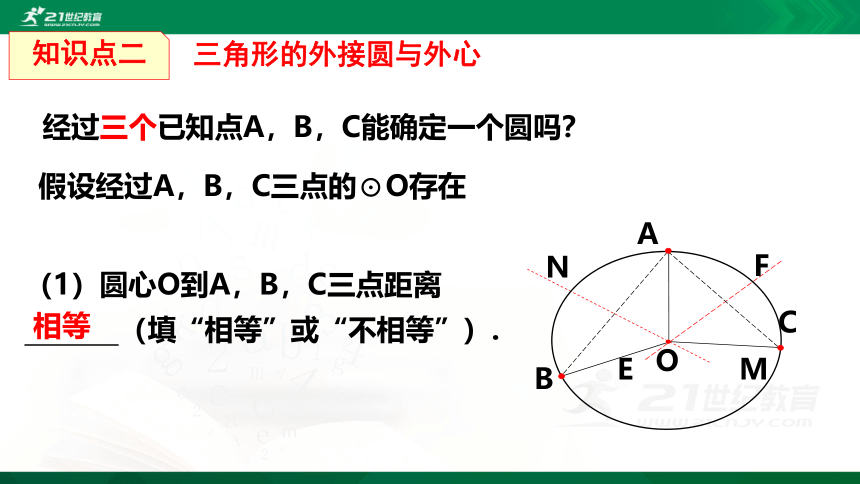
经过三个已知点A,B,C能确定一个圆吗?
假设经过A,B,C三点的⊙O存在
(1)圆心O到A,B,C三点距离
(填“相等”或“不相等”).
N
M
F
E
O
A
B
C
相等
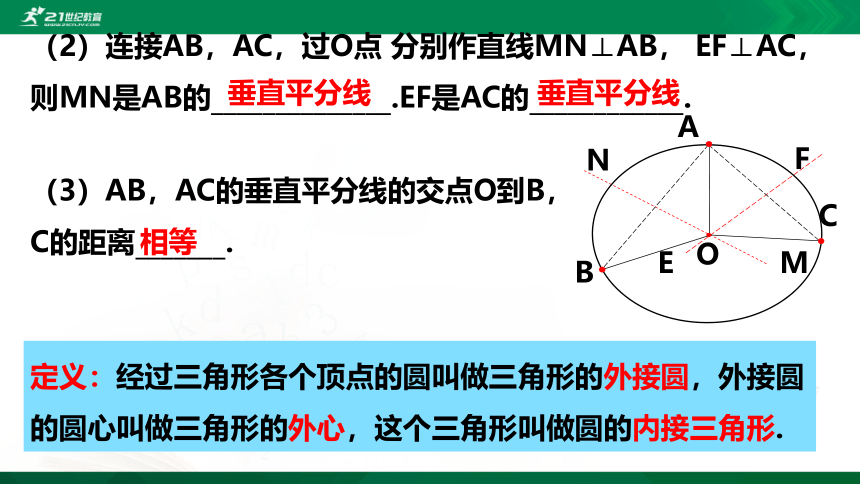
(2)连接AB,AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的______________.EF是AC的____________.
(3)AB,AC的垂直平分线的交点O到B,C的距离_______.
N
M
F
E
O
A
B
C
垂直平分线
垂直平分线
相等
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到角形的三个顶点的距离相等.
C
A
B
O
定义:三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一点的距离为半径作圆即可.
例2 如图,△ABC内接于⊙O,∠C=45°,AB=4,求⊙O的半径.
例题讲解
解:
方法一:如图,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
例3 如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心,则四边形ABCD一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
解:∵圆内接四边形ABCD的对角线交点恰好是该圆的圆心, ∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD一定是矩形. 故选B.
例题讲解
1 下列说法中正确的是( )
A.两个点确定一个圆 B.三个点确定一个圆
C.四个点确定一个圆 D.不共线的三个点确定一个圆
课堂练习
2 下列四边形中,一定有外接圆的是( )
A.平行四边形 B.菱形
C.矩形 D.梯形
3 小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A.2 cm B.4 cm
C.6 cm D.8 cm
4 下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;② 任何圆有且只有一个内接三角形;③三角形的外心不一定在三角形内;④三角形的外心到三角形三边的距离相等;⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4
5 请你在如图所示的12×12的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的 个格点.
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.
(2)经过一个已知点能作无数个圆!
(3)经过两个已知点A、B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上.
(4)不在同一直线上的三个点确定一个圆.
(5)外接圆,外心的概念.
课堂小结
谢谢聆听
第三章 圆
2020-2021北师大版九年级数学下册
1 了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法;
2 了解三角形的外接圆、三角形的外心等概念.
3 经历不在同一直线上的三个点确定一个圆的探索过程,
培养学生的探索能力.
学习目标
1 过一点可以作几条直线?
2 过几点可确定一条直线?
思考:过几点可以确定一个圆呢?
新课导入
确定圆的条件
知识点一
1 经过一个已知点A能确定一个圆吗?
A
经过一点可作无数个圆.
探究新知
2 经过两个已知点A,B能确定一个圆吗?
A
B
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
它们的圆心都在线段AB的垂直平分线上.
经过两个已知点A,B能作无数个圆.
如图所示,点A,B,C 在同一条直线上,点D 在直线AB 外,过这四个点中的任意三个点,能画圆的个数是( )
A.1 B.2 C.3 D.4
例1
C
例题讲解
解:过不在同一条直线上的三点确定一个圆,在点A,B,C,D 四个点中取三个点的方法有:点A,B,C;点A,B,D;点B,C,D;点A,C,D,共四组. 又因A,B,C 三点在同一条直线上,故过这四个点中的任意三个点能画圆的个数为3.
三角形的外接圆与外心
知识点二
经过三个已知点A,B,C能确定一个圆吗?
假设经过A,B,C三点的⊙O存在
(1)圆心O到A,B,C三点距离
(填“相等”或“不相等”).
N
M
F
E
O
A
B
C
相等
(2)连接AB,AC,过O点 分别作直线MN⊥AB, EF⊥AC,则MN是AB的______________.EF是AC的____________.
(3)AB,AC的垂直平分线的交点O到B,C的距离_______.
N
M
F
E
O
A
B
C
垂直平分线
垂直平分线
相等
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到角形的三个顶点的距离相等.
C
A
B
O
定义:三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一点的距离为半径作圆即可.
例2 如图,△ABC内接于⊙O,∠C=45°,AB=4,求⊙O的半径.
例题讲解
解:
方法一:如图,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
例3 如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心,则四边形ABCD一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
解:∵圆内接四边形ABCD的对角线交点恰好是该圆的圆心, ∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD一定是矩形. 故选B.
例题讲解
1 下列说法中正确的是( )
A.两个点确定一个圆 B.三个点确定一个圆
C.四个点确定一个圆 D.不共线的三个点确定一个圆
课堂练习
2 下列四边形中,一定有外接圆的是( )
A.平行四边形 B.菱形
C.矩形 D.梯形
3 小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A.2 cm B.4 cm
C.6 cm D.8 cm
4 下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;② 任何圆有且只有一个内接三角形;③三角形的外心不一定在三角形内;④三角形的外心到三角形三边的距离相等;⑤经过三点确定一个圆.
A.1 B.2 C.3 D.4
5 请你在如图所示的12×12的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的 个格点.
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.
(2)经过一个已知点能作无数个圆!
(3)经过两个已知点A、B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上.
(4)不在同一直线上的三个点确定一个圆.
(5)外接圆,外心的概念.
课堂小结
谢谢聆听
