2021年春青岛版八年级数学下册6.1平行四边形及其性质自主学习同步测评(Word版含答案)
文档属性
| 名称 | 2021年春青岛版八年级数学下册6.1平行四边形及其性质自主学习同步测评(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 211.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 00:00:00 | ||
图片预览



文档简介
2021年青岛版八年级数学下册6.1平行四边形及其性质自主学习同步测评2(附答案)
1.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6 B.15 C.30 D.60
2.如图,已知平行四边形OABC的顶点A,C分别在直线x=1和x=4上,点O是坐标原点,则点B的横坐标为( )
A.3 B.4 C.5 D.10
3.在?ABCD中,若∠A+∠C=260°,则∠C的度数为( )
A.50° B.100° C.120° D.130°
4.在平行四边形ABCD中,若∠A=60°,则∠B的度数是( )
A.30° B.60° C.90° D.120°
5.如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下结论中不正确的是( )
A.△CDF≌△EBC B.∠ECF=60°
C.△ECF是等边三角形 D.CG⊥AE
6.已知?ABCD的周长为56,AB=4,则BC=( )
A.4 B.12 C.24 D.28
7.如图,P为平行四边形ABCD内一点,过点P分别作AB,AD的平行线,交平行四边形ABCD的四边于E、F、G、H四点,若平行四边形BHPE面积为6,平行四边形GPFD面积为4,则△APC的面积为( )
A. B. C.1 D.2
8.如图,在?ABCD中,BE⊥CD,BF⊥AD,∠EBF=45°,CE=3,DF=1,则?ABCD的面积是( )
A.18﹣3 B.15+3 C.15﹣3 D.18+3
9.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE的度数为( )
A.53° B.37° C.47° D.123°
10.已知平行四边形两邻边长16,20,若两个长边间距离为8,则两条短边间距离( )
A.4 B.5 C.10 D.8
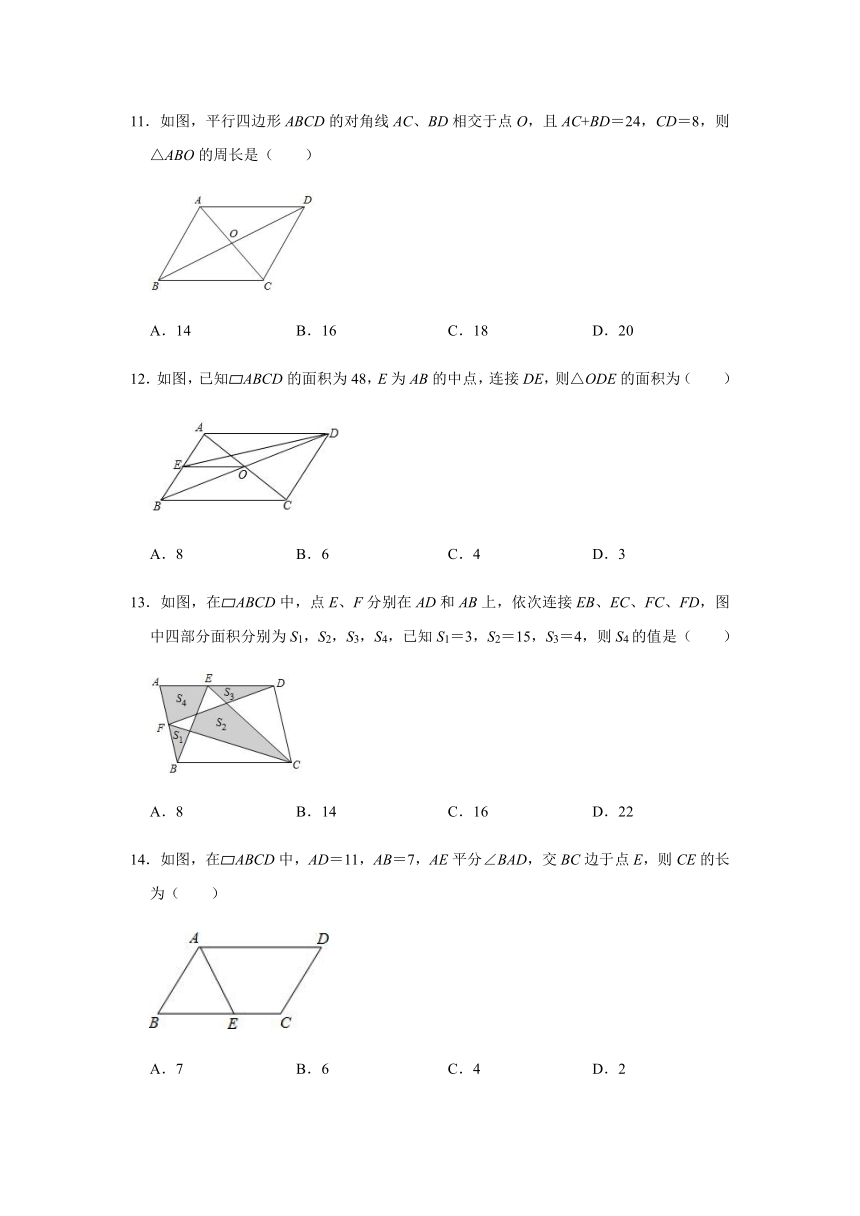
11.如图,平行四边形ABCD的对角线AC、BD相交于点O,且AC+BD=24,CD=8,则△ABO的周长是( )
A.14 B.16 C.18 D.20
12.如图,已知?ABCD的面积为48,E为AB的中点,连接DE,则△ODE的面积为( )
A.8 B.6 C.4 D.3
13.如图,在?ABCD中,点E、F分别在AD和AB上,依次连接EB、EC、FC、FD,图中四部分面积分别为S1,S2,S3,S4,已知S1=3,S2=15,S3=4,则S4的值是( )
A.8 B.14 C.16 D.22
14.如图,在?ABCD中,AD=11,AB=7,AE平分∠BAD,交BC边于点E,则CE的长为( )
A.7 B.6 C.4 D.2
15.如图,?ABCD的对角线交点是直角坐标系的原点,BC∥x轴,若顶点C坐标是(5,3),BC=8,则顶点D的坐标是( )
A.(3,﹣3) B.(﹣3,3) C.(5,﹣3) D.(3,﹣5)
16.已知?ABCD的对角线AC与BD相交于O,BO+AO=5,则AC+BD等于( )
A.8 B.4 C.14 D.10
17.如图,若?AFPE、?BGPF、?EPHD的面积分别为15、6、25,则三角形DFG的面积是( )
A.20 B.15.5 C.23 D.25
18.如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O,已知S?ABCD=a,S?EFGH=b(a<b),则SBCEG为( )
A.b﹣a B.(b﹣a) C.a D.b
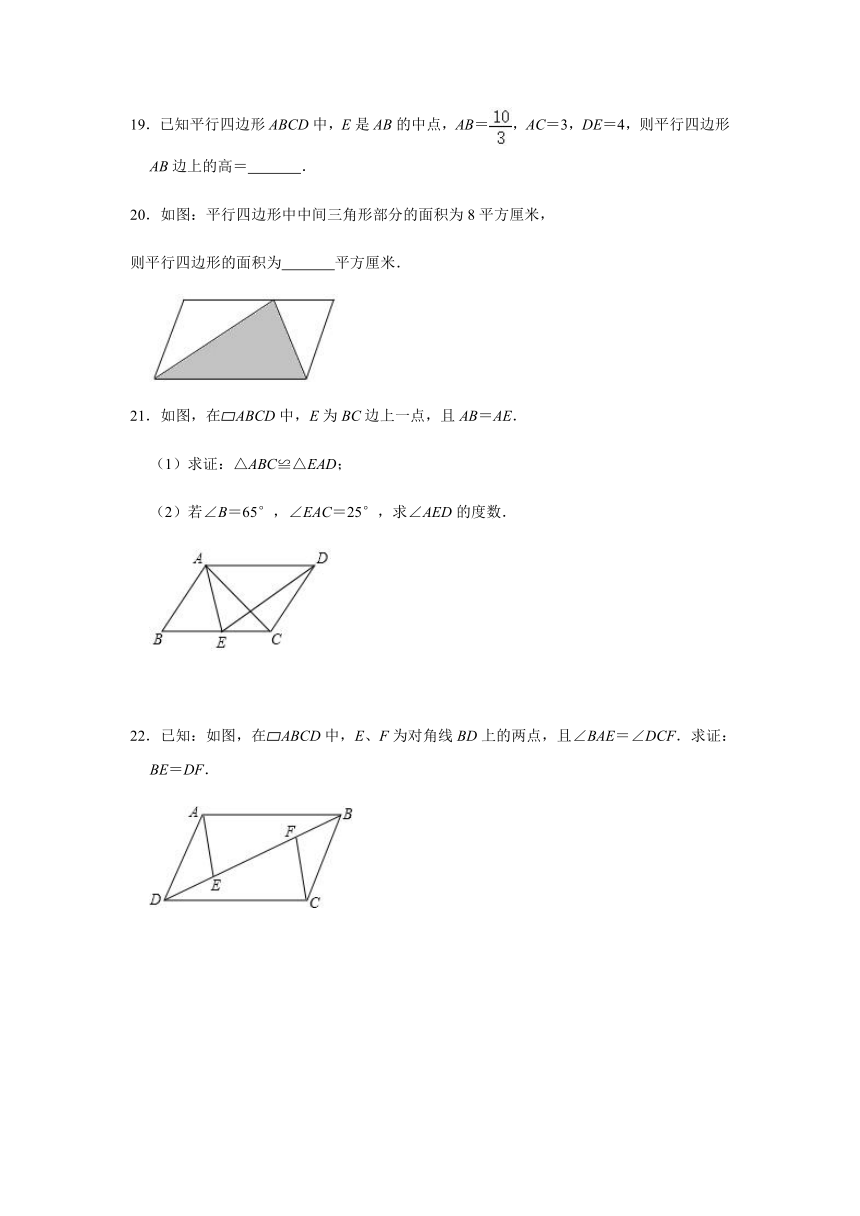
19.已知平行四边形ABCD中,E是AB的中点,AB=,AC=3,DE=4,则平行四边形AB边上的高= .
20.如图:平行四边形中中间三角形部分的面积为8平方厘米,
则平行四边形的面积为 平方厘米.
21.如图,在?ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.
22.已知:如图,在?ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.求证:BE=DF.
23.如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
24.如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.求证:∠BAC=∠BFC.
25.如图,?ABCD中,∠BAD的平分线AE交DC于点E.
(1)试说明AD=DE;
(2)若AB:CB=3:2,CE=5cm,求?ABCD的周长.
参考答案
1.解:观察并结合平行四边形的性质可知,图中下半部分的阴影面积等于上半部分的空白面积,
∴S阴影=S?ABCD,
∵BC=10,BC边上的高为6,
∴S?ABCD=10×6=60,
∴S阴影=×60=30.
故选:C.
2.解:过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,如图所示:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=1与直线x=4均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,,
∴△OAF≌△BCD(ASA).
∴BD=OF=1,
∴点B的横坐标为:OE=4+BD=4+1=5,
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=260°,
∴∠C=130°,
故选:D.
4.解:如图,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣60°=120°.
故选:D.
5.解:∵△ABE、△ADF是等边三角形,
∴FD=AD,BE=AB,
∵AD=BC,AB=DC,
∴FD=BC,BE=DC,
∵∠CBE=∠FDC,∠FDA=∠ABE,
∴∠CDF=∠EB,
∴△CDF≌△EBC(SAS),故A正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°﹣∠CDA)=300°﹣∠CDA,
∠FDC=360°﹣∠FDA﹣∠ADC=300°﹣∠CDA,
∴∠CDF=∠EAF,
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC(SAS),
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故C正确;
∴∠ECF=60°,故B正确;
在等边三角形ABE中,
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段,
∴如果CG⊥AE,则G是AE的中点,
∴∠ABG=30°,∠ABC=150°,
而题目缺少这个条件,
∴CG⊥AE不能求证,故D错误.
故选:D.
6.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵?ABCD的周长为56,
∴AB+BC=28,
∵AB=4,
∴BC=24,
故选:C.
7.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,S△ABC=S△ACD,
∵EF∥AD,GH∥AB,
∴EF∥AD∥BC,AB∥CD∥GH,
∴四边形EPGA、四边形GPFD、四边形EPHB、四边形PHCF均为平行四边形,
∴S△AEP=S△AGP=S平行四边形AEPG,S△PHC=S△PCF=S平行四边形PHCF,
∵S△ABC=S△AEP+S平行四边形BHPE+S△PHC﹣S△APC①,S△ACD=S△AGP+S平行四边形GPFD+S△PFC+S△APC②,
∴②﹣①得:S平行四边形GPFD﹣S平行四边形BHPE+2S△APC=0,
即2S△APC=6﹣4=2,
∴S△APC=1.
故选:C.
8.解:∵BE⊥CD,BF⊥AD,
∴∠BEC=90°,∠BED=∠BFD=90°,
∵∠EBF=45°,
∴∠D=360°﹣90°﹣90°=135°,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠C=180°﹣∠D=45°,
∴∠A=∠C=45°,
∵CE=3,
∴BE=EC=3,
∴BC=3,
∵DF=1,
∴AF=BF=3﹣1,
∴?ABCD的面积是AD×BF=3×(3﹣1)=18﹣3.
故选:A.
9.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B+∠BAD=180°,
∵∠BAD=127°
∴∠B=53°
∵CE⊥AB,
∴∠E=90°
∴∠BCE=90°﹣∠B=90°﹣53°=37°;
故选:B.
10.解:设两短边间的距离为x,
∵平行四边形两邻边分别为16,20,两长边间的距离为8,
∴20×8=16x,
解得:x=10.
∴两短边间的距离为10.
故选:C.
11.解:∵四边形ABCD为平行四边形,
∴AB=CD=8,OA=OC=AC,OB=OD=BD,
∵AC+BD=24,
∴AB+OA+OB
=8+AC+BD
=8+12
=20,
∴△ABO的周长是20.
故选:D.
12.解:∵E为AB的中点,
∴S△AOE=S△AOB,
∵平行四边形ABCD的面积为48,
∴OB=OD,OA=OC,S△AOB=S?ABCD=×48=12,
∴S△AOE=6,
∴S△ODE=S△AOE=6.
故选:B.
13.解:设平行四边形的面积为S,则S△CBE=S△CDF=S,
由图形可知,△CDF面积+△CBE面积+(S1+S4+S3)﹣S2=平行四边形ABCD的面积,
∴S=S△CBE+S△CDF+3+S4+4﹣15,
即S=S+S+3+S4+4﹣15,
解得S4=8,
故选:A.
14.解:在?ABCD中,BC=AD=11,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠AEB=∠BAE,
∴BE=AB=7,
∴CE=BC﹣BE=11﹣7=4.
故选:C.
15.解:∵平行四边形ABCD的对角线交点是直角坐标系的原点,BC∥x轴,BC=8,C(5,3),
∴B(﹣3,3),B与D关于原点O对称,
∴D(3,﹣3);
故选:A.
16.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴AC=2AO,BD=2BO,
∵BO+AO=5,
∴AC+BD=2(AO+BO)=10,
故选:D.
17.解:∵?AFPE、?BGPF、?EPHD的面积分别为15、6、25,
∴AB∥CE∥CD,AD∥FH∥BC,PF:PH=15:25=3:5,
∴四边形ADHF、四边形CDEG是平行四边形,?CGPH的面积=5×=10,
∴?ABCD的面积=15+6+25+10=56,△ADF的面积=?ADHF的面积=(15+25)=20,
△CDG的面积=?CDEG的面积=(25+10)=17.5,△BFG的面积=?BGPF的面积=×6=3,
∴阴影部分的面积=56﹣20﹣17.5=3=15.5;
故选:B.
18.解:∵平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,
∴EH=BC,EH∥BC,
∴∠EHO=∠CBO,
在△EHO与△CBO中,,
∴△EHO≌△CBO(AAS),
∴△EHO面积=△CBO面积,
∴S阴影=S△EGH=S?EFGH=b;
故选:D.
19.解:如图,设AC与DE相交于点O,
∵四边形ABCD是平行四边形,
∴AE∥CD,
∴△AOE∽△COD,
∵E是AB的中点,
∴相似比为1:2,
∴==,
∵AC=3,DE=4,
∴OA=1,OE=,
∵AE=AB==,
∴OA2+OE2=AE2,
∴∠AOE=90°,
∴AC⊥DE,
∵OD=4﹣=,
∴S△ADC=AC?OD=4,
∴S平行四边形ABCD=2S△ADC=8,
∵AB=,
∴平行四边形AB边上的高=8÷=.
故答案为:.
20.解:∵平行四边形中阴影部分的面积=平行四边形的面积,
∴平行四边形的面积=2×8=16(平方厘米);
故答案为:16.
21.(1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS).
(2)解:∵AB=AE,
∴∠B=∠AEB,
∴∠BAE=50°,
∴∠BAC=∠BAE+∠EAC=50°+25°=75°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=75°.
22.证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中,
∴△ABE≌△DCF,
∴BE=DF.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF===2,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=AE?BF=×4×2=4.
24.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
在△BAE和△CFE中,,
∴△BAE≌△CFE,
∴AB=CF,
又∵AB∥CF,
∴四边形ABFC是平行四边形,
∴∠BAC=∠BFC.
25.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DEA=∠DAE,
∴AD=DE.
(2)解:设AB=3kcm,CB=2kcm,
∵AD=DE,DC=AB,
∴AB﹣AD=CE=5cm,
∴3k﹣2k=5,
k=5,
∴AB=DC=15cm,AD=BC=10cm,
∴平行四边形ABCD的周长是:AB+BC+CD+AD=15cm+10cm+15cm+10cm=50cm.
1.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6 B.15 C.30 D.60
2.如图,已知平行四边形OABC的顶点A,C分别在直线x=1和x=4上,点O是坐标原点,则点B的横坐标为( )
A.3 B.4 C.5 D.10
3.在?ABCD中,若∠A+∠C=260°,则∠C的度数为( )
A.50° B.100° C.120° D.130°
4.在平行四边形ABCD中,若∠A=60°,则∠B的度数是( )
A.30° B.60° C.90° D.120°
5.如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下结论中不正确的是( )
A.△CDF≌△EBC B.∠ECF=60°
C.△ECF是等边三角形 D.CG⊥AE
6.已知?ABCD的周长为56,AB=4,则BC=( )
A.4 B.12 C.24 D.28
7.如图,P为平行四边形ABCD内一点,过点P分别作AB,AD的平行线,交平行四边形ABCD的四边于E、F、G、H四点,若平行四边形BHPE面积为6,平行四边形GPFD面积为4,则△APC的面积为( )
A. B. C.1 D.2
8.如图,在?ABCD中,BE⊥CD,BF⊥AD,∠EBF=45°,CE=3,DF=1,则?ABCD的面积是( )
A.18﹣3 B.15+3 C.15﹣3 D.18+3
9.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE的度数为( )
A.53° B.37° C.47° D.123°
10.已知平行四边形两邻边长16,20,若两个长边间距离为8,则两条短边间距离( )
A.4 B.5 C.10 D.8
11.如图,平行四边形ABCD的对角线AC、BD相交于点O,且AC+BD=24,CD=8,则△ABO的周长是( )
A.14 B.16 C.18 D.20
12.如图,已知?ABCD的面积为48,E为AB的中点,连接DE,则△ODE的面积为( )
A.8 B.6 C.4 D.3
13.如图,在?ABCD中,点E、F分别在AD和AB上,依次连接EB、EC、FC、FD,图中四部分面积分别为S1,S2,S3,S4,已知S1=3,S2=15,S3=4,则S4的值是( )
A.8 B.14 C.16 D.22
14.如图,在?ABCD中,AD=11,AB=7,AE平分∠BAD,交BC边于点E,则CE的长为( )
A.7 B.6 C.4 D.2
15.如图,?ABCD的对角线交点是直角坐标系的原点,BC∥x轴,若顶点C坐标是(5,3),BC=8,则顶点D的坐标是( )
A.(3,﹣3) B.(﹣3,3) C.(5,﹣3) D.(3,﹣5)
16.已知?ABCD的对角线AC与BD相交于O,BO+AO=5,则AC+BD等于( )
A.8 B.4 C.14 D.10
17.如图,若?AFPE、?BGPF、?EPHD的面积分别为15、6、25,则三角形DFG的面积是( )
A.20 B.15.5 C.23 D.25
18.如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O,已知S?ABCD=a,S?EFGH=b(a<b),则SBCEG为( )
A.b﹣a B.(b﹣a) C.a D.b
19.已知平行四边形ABCD中,E是AB的中点,AB=,AC=3,DE=4,则平行四边形AB边上的高= .
20.如图:平行四边形中中间三角形部分的面积为8平方厘米,
则平行四边形的面积为 平方厘米.
21.如图,在?ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.
22.已知:如图,在?ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.求证:BE=DF.
23.如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
24.如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.求证:∠BAC=∠BFC.
25.如图,?ABCD中,∠BAD的平分线AE交DC于点E.
(1)试说明AD=DE;
(2)若AB:CB=3:2,CE=5cm,求?ABCD的周长.
参考答案
1.解:观察并结合平行四边形的性质可知,图中下半部分的阴影面积等于上半部分的空白面积,
∴S阴影=S?ABCD,
∵BC=10,BC边上的高为6,
∴S?ABCD=10×6=60,
∴S阴影=×60=30.
故选:C.
2.解:过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,如图所示:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=1与直线x=4均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,,
∴△OAF≌△BCD(ASA).
∴BD=OF=1,
∴点B的横坐标为:OE=4+BD=4+1=5,
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=260°,
∴∠C=130°,
故选:D.
4.解:如图,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣60°=120°.
故选:D.
5.解:∵△ABE、△ADF是等边三角形,
∴FD=AD,BE=AB,
∵AD=BC,AB=DC,
∴FD=BC,BE=DC,
∵∠CBE=∠FDC,∠FDA=∠ABE,
∴∠CDF=∠EB,
∴△CDF≌△EBC(SAS),故A正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°﹣∠CDA)=300°﹣∠CDA,
∠FDC=360°﹣∠FDA﹣∠ADC=300°﹣∠CDA,
∴∠CDF=∠EAF,
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC(SAS),
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故C正确;
∴∠ECF=60°,故B正确;
在等边三角形ABE中,
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段,
∴如果CG⊥AE,则G是AE的中点,
∴∠ABG=30°,∠ABC=150°,
而题目缺少这个条件,
∴CG⊥AE不能求证,故D错误.
故选:D.
6.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵?ABCD的周长为56,
∴AB+BC=28,
∵AB=4,
∴BC=24,
故选:C.
7.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,S△ABC=S△ACD,
∵EF∥AD,GH∥AB,
∴EF∥AD∥BC,AB∥CD∥GH,
∴四边形EPGA、四边形GPFD、四边形EPHB、四边形PHCF均为平行四边形,
∴S△AEP=S△AGP=S平行四边形AEPG,S△PHC=S△PCF=S平行四边形PHCF,
∵S△ABC=S△AEP+S平行四边形BHPE+S△PHC﹣S△APC①,S△ACD=S△AGP+S平行四边形GPFD+S△PFC+S△APC②,
∴②﹣①得:S平行四边形GPFD﹣S平行四边形BHPE+2S△APC=0,
即2S△APC=6﹣4=2,
∴S△APC=1.
故选:C.
8.解:∵BE⊥CD,BF⊥AD,
∴∠BEC=90°,∠BED=∠BFD=90°,
∵∠EBF=45°,
∴∠D=360°﹣90°﹣90°=135°,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠C=180°﹣∠D=45°,
∴∠A=∠C=45°,
∵CE=3,
∴BE=EC=3,
∴BC=3,
∵DF=1,
∴AF=BF=3﹣1,
∴?ABCD的面积是AD×BF=3×(3﹣1)=18﹣3.
故选:A.
9.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B+∠BAD=180°,
∵∠BAD=127°
∴∠B=53°
∵CE⊥AB,
∴∠E=90°
∴∠BCE=90°﹣∠B=90°﹣53°=37°;
故选:B.
10.解:设两短边间的距离为x,
∵平行四边形两邻边分别为16,20,两长边间的距离为8,
∴20×8=16x,
解得:x=10.
∴两短边间的距离为10.
故选:C.
11.解:∵四边形ABCD为平行四边形,
∴AB=CD=8,OA=OC=AC,OB=OD=BD,
∵AC+BD=24,
∴AB+OA+OB
=8+AC+BD
=8+12
=20,
∴△ABO的周长是20.
故选:D.
12.解:∵E为AB的中点,
∴S△AOE=S△AOB,
∵平行四边形ABCD的面积为48,
∴OB=OD,OA=OC,S△AOB=S?ABCD=×48=12,
∴S△AOE=6,
∴S△ODE=S△AOE=6.
故选:B.
13.解:设平行四边形的面积为S,则S△CBE=S△CDF=S,
由图形可知,△CDF面积+△CBE面积+(S1+S4+S3)﹣S2=平行四边形ABCD的面积,
∴S=S△CBE+S△CDF+3+S4+4﹣15,
即S=S+S+3+S4+4﹣15,
解得S4=8,
故选:A.
14.解:在?ABCD中,BC=AD=11,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠AEB=∠BAE,
∴BE=AB=7,
∴CE=BC﹣BE=11﹣7=4.
故选:C.
15.解:∵平行四边形ABCD的对角线交点是直角坐标系的原点,BC∥x轴,BC=8,C(5,3),
∴B(﹣3,3),B与D关于原点O对称,
∴D(3,﹣3);
故选:A.
16.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴AC=2AO,BD=2BO,
∵BO+AO=5,
∴AC+BD=2(AO+BO)=10,
故选:D.
17.解:∵?AFPE、?BGPF、?EPHD的面积分别为15、6、25,
∴AB∥CE∥CD,AD∥FH∥BC,PF:PH=15:25=3:5,
∴四边形ADHF、四边形CDEG是平行四边形,?CGPH的面积=5×=10,
∴?ABCD的面积=15+6+25+10=56,△ADF的面积=?ADHF的面积=(15+25)=20,
△CDG的面积=?CDEG的面积=(25+10)=17.5,△BFG的面积=?BGPF的面积=×6=3,
∴阴影部分的面积=56﹣20﹣17.5=3=15.5;
故选:B.
18.解:∵平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,
∴EH=BC,EH∥BC,
∴∠EHO=∠CBO,
在△EHO与△CBO中,,
∴△EHO≌△CBO(AAS),
∴△EHO面积=△CBO面积,
∴S阴影=S△EGH=S?EFGH=b;
故选:D.
19.解:如图,设AC与DE相交于点O,
∵四边形ABCD是平行四边形,
∴AE∥CD,
∴△AOE∽△COD,
∵E是AB的中点,
∴相似比为1:2,
∴==,
∵AC=3,DE=4,
∴OA=1,OE=,
∵AE=AB==,
∴OA2+OE2=AE2,
∴∠AOE=90°,
∴AC⊥DE,
∵OD=4﹣=,
∴S△ADC=AC?OD=4,
∴S平行四边形ABCD=2S△ADC=8,
∵AB=,
∴平行四边形AB边上的高=8÷=.
故答案为:.
20.解:∵平行四边形中阴影部分的面积=平行四边形的面积,
∴平行四边形的面积=2×8=16(平方厘米);
故答案为:16.
21.(1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS).
(2)解:∵AB=AE,
∴∠B=∠AEB,
∴∠BAE=50°,
∴∠BAC=∠BAE+∠EAC=50°+25°=75°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=75°.
22.证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中,
∴△ABE≌△DCF,
∴BE=DF.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF===2,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=AE?BF=×4×2=4.
24.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
在△BAE和△CFE中,,
∴△BAE≌△CFE,
∴AB=CF,
又∵AB∥CF,
∴四边形ABFC是平行四边形,
∴∠BAC=∠BFC.
25.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DEA=∠DAE,
∴AD=DE.
(2)解:设AB=3kcm,CB=2kcm,
∵AD=DE,DC=AB,
∴AB﹣AD=CE=5cm,
∴3k﹣2k=5,
k=5,
∴AB=DC=15cm,AD=BC=10cm,
∴平行四边形ABCD的周长是:AB+BC+CD+AD=15cm+10cm+15cm+10cm=50cm.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
