人教版 八年级数学下册 第18章 平行四边形 综合训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学下册 第18章 平行四边形 综合训练(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 472.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 00:00:00 | ||
图片预览



文档简介
人教版 八年级数学下册 第18章 平行四边形 综合训练
一、选择题
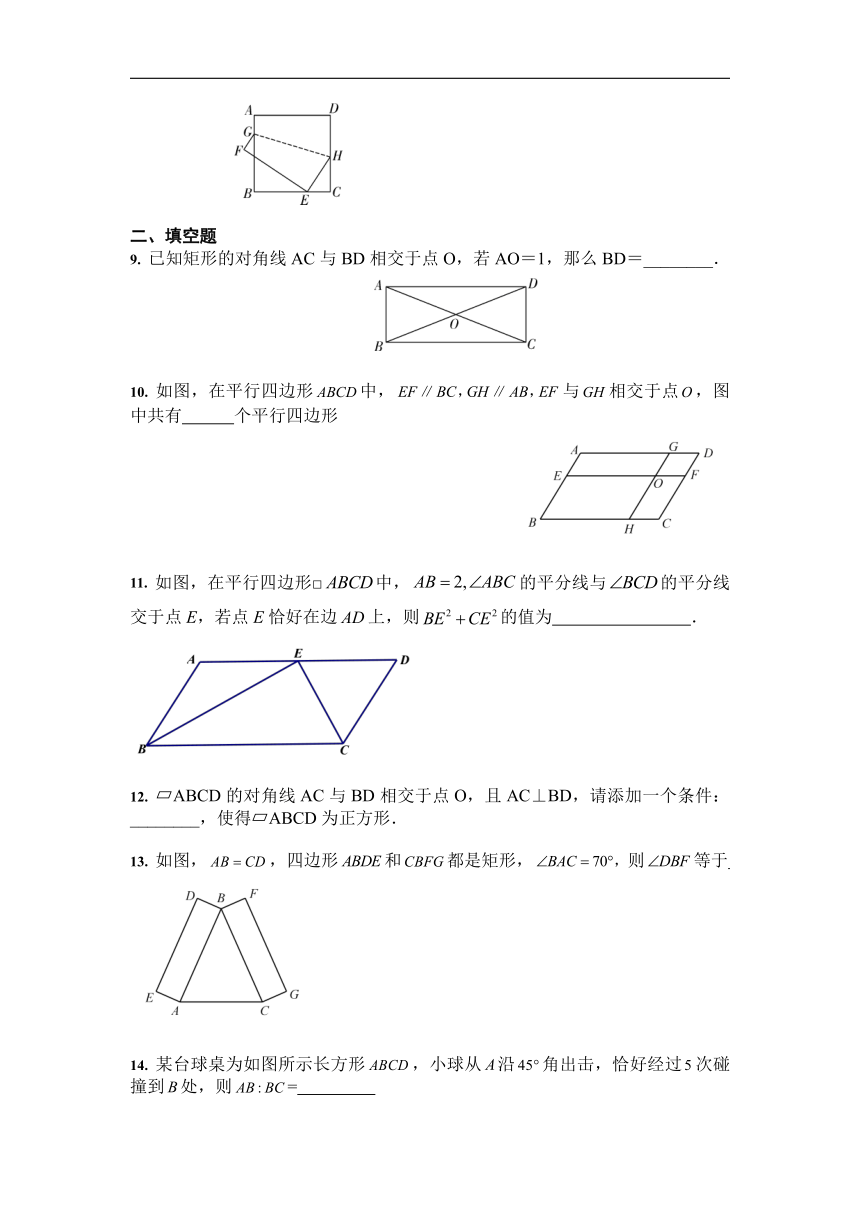
1. 如图,在ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为
A.12 B.15 C.18 D.21
2. (2020·毕节)如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm,则EF的长是( )
A.2.2 cm B.2.3 cm C.2.4 cm D.2.5 cm
3. 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处.若∠2=40°,则图中∠1的度数为( )
A. 115° B. 120° C. 130° D. 140°
4. (2020·绍兴)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形 B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形 D.平行四边形→菱形→正方形→矩形
5. (2020·乐山)如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于E,连接OA,则四边形AOED的周长为( )
A.9+2 B.9+ C.7+2 D.8
6. 如图,在平行四边中,、为对角线,,边上的高为,则阴影部分的面积为( ).
A.3 B.6 C.12 D.24
7. 如图,点分别在的边上,且
,,有黑、白两只蚂蚁,它们同时同速从点出发,黑蚂蚁沿路线爬行,白蚂蚁沿路线爬行,那么( )
黑蚂蚁先回到点
白蚂蚁先回到点
两只蚂蚁同时回到点
哪只蚂蚁先回到点视各点的位置而定
8. 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=2∶1,则线段CH的长是( )
A. 3 B. 4 C. 5 D. 6
二、填空题
9. 已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD=________.
10. 如图,在平行四边形中,与相交于点,图中共有 个平行四边形
11. 如图,在平行四边形□中,的平分线与的平分线交于点E,若点E恰好在边上,则的值为 .
12. ?ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:________,使得?ABCD为正方形.
13. 如图,,四边形和都是矩形,则等于
14. 某台球桌为如图所示长方形,小球从沿角出击,恰好经过次碰撞到处,则=
三、解答题
15. 如图,四边形为平行四边形,即,.通过证明三角形全等来说明:
⑴,.(对边相等)
⑵,.(对角线互相平分)
16. 如图,、分别是平行四边形的、边上的点,且.
⑴求证:≌;
⑵若、分别是、的中点,连接、,试判断四边形是怎样的四边形,并证明你的结论.
17. 如图,将?ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
18. 如图,是矩形的对角线交点,过点作分别交、于、,若,,求四边形的面积.
人教版 八年级数学下册 第18章 平行四边形 综合训练-答案
一、选择题
1. 【答案】C
【解析】由折叠可得,∠ACD=∠ACE=90°,∴∠BAC=90°,
又∵∠B=60°,∴∠ACB=30°,∴BC=2AB=6,∴AD=6,
由折叠可得,∠E=∠D=∠B=60°,
∴∠DAE=60°,∴△ADE是等边三角形,
∴△ADE的周长为6×3=18,
故选C.
2. 【答案】D,
【解析】本题考查矩形的性质,三角形中位线定理.
解:矩形ABCD中,∵AB=6cm,∴DC=6cm,∵∠BCD=90°,BC=8cm,∴BD=10.
∵对角线AC,BD相交于点O,∴OD=BD=5.∵点E,F分别是AO,AD的中点,∴EF=2.5.故选D.
3. 【答案】A 【解析】由折叠的性质知∠EA′B′=∠A=90°,∵∠2=40°,∴∠B′A′C=50°,∴∠EA′D=40°,∠DEA′=50°,∴∠AEA′=130°,∴∠AEF=∠FEA′=∠AEA′=65°,∵AD∥BC,∴∠1=180°-65°=115°.
4. 【答案】B
【解析】本题考查了特殊四边形的判定.当点E从点A出发沿AB向点B运动时,四边形AECF的形状依次如下图所示.因此本题选B.
5. 【答案】B
【解析】由已知及菱形的性质求得∠ABD=∠CDB=30?,AO⊥BD,利用含30?的直角三角形边的关系分别求得AO、DO、OE、DE,进而求得四边形AOED的周长.∵四边形ABCD是菱形,O是对角线AC的中点,∴AO⊥BD,AD=AB=4,AB∥DC;∵∠BAD=120?,∴∠ABD=∠ADB=∠CDB=30?;∵OE⊥DC,∴在Rt△AOD中,AD=4,AO=AD=2,DO==2;在Rt△DEO中,OE=OD=,DE==3,∴四边形AOED的周长为AO+OE+DE+AD=2++3+4=9+.
6. 【答案】C
7. 【答案】C
【解析】可知四边形均为平行四边形,可知选C
8. 【答案】B 【解析】设CH=x,∵BE∶EC=2∶1,BC=9,∴EC=3,由折叠可知,EH=DH=9-x,在Rt△ECH中,由勾股定理得:(9-x)2=32+x2,解得:x=4.
二、填空题
9. 【答案】2 【解析】根据“矩形的对角线相等且互相平分”进行解题便可.∵四边形ABCD是矩形,∴BD=AC=2OA,∵OA=1,∴BD=2.
10. 【答案】个
11. 【答案】16
【解析】∵四边形ABCD是平行四边形,∴AB=CD=2,AD=BC,AD∥BC,AB∥CD,∴∠ABC+∠BCD=180°, ∠AEB=∠EBC,∠DEC=∠ECB.又∵BE、CE分别是∠ABC与∠DCB的平分线,∴∠ABE=∠EBC,∠DCE=∠ECB,∴∠EBC+∠BCE=90°,∠ABE=∠AEB,∠DCE=∠DEC,∴AB=AE=2,DC=DE=2,
12. 【答案】∠BAD=90°(答案不唯一) 【解析】∵?ABCD的对角线AC与BD相交于点O,且AC⊥BD,∴?ABCD是菱形,当∠BAD=90°时,菱形ABCD为正方形.故可添加条件:∠BAD=90°.
13. 【答案】
14. 【答案】
【解析】由图形可知:可推出
三、解答题
15. 【答案】
⑴ ∵,
∴,
在和中,
∴
∴,.
⑵ 在和中,
∴,.
16. 【答案】
⑴由是平行四边形可知,,
又,故≌
⑵由(1)可知,,
又,,∴
而∥,∴有
∴,∴∥
∴四边形为平行四边形
17. 【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥FC.(2分)
∵F是BC的中点,
∴FC=BC=AD,
∵DE=AD,∴FC=DE,(4分)
∴四边形CEDF是平行四边形.(5分)
(2)
解图
解:如解图,过点D作DH⊥BC于点H.
由(1)知四边形DECF是平行四边形,
∴DF=CE.(6分)
∵四边形ABCD是平行四边形,∠A=60°,AB=3,AD=4,
∴BC=4,CD=3,∠BCD=60°,(8分)
在Rt△DHC中,HC=DC·cos∠HCD=,
DH=DC·sin∠HCD=,
∵F是BC的中点,
∴FC=2,
∴FH=FC-HC=2-=,(10分)
在Rt△DFH中,由勾股定理得DF==
=,
∴CE=.(12分)
18. 【答案】
【解析】由为矩形可知,
又∵∥,∴
又,∴≌. 故
从而可知为菱形,∴.
又∵,
∴在直角中,由勾股定理有,
解得.故四边形的面积为()
一、选择题
1. 如图,在ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为
A.12 B.15 C.18 D.21
2. (2020·毕节)如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm,则EF的长是( )
A.2.2 cm B.2.3 cm C.2.4 cm D.2.5 cm
3. 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处.若∠2=40°,则图中∠1的度数为( )
A. 115° B. 120° C. 130° D. 140°
4. (2020·绍兴)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形 B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形 D.平行四边形→菱形→正方形→矩形
5. (2020·乐山)如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于E,连接OA,则四边形AOED的周长为( )
A.9+2 B.9+ C.7+2 D.8
6. 如图,在平行四边中,、为对角线,,边上的高为,则阴影部分的面积为( ).
A.3 B.6 C.12 D.24
7. 如图,点分别在的边上,且
,,有黑、白两只蚂蚁,它们同时同速从点出发,黑蚂蚁沿路线爬行,白蚂蚁沿路线爬行,那么( )
黑蚂蚁先回到点
白蚂蚁先回到点
两只蚂蚁同时回到点
哪只蚂蚁先回到点视各点的位置而定
8. 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=2∶1,则线段CH的长是( )
A. 3 B. 4 C. 5 D. 6
二、填空题
9. 已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD=________.
10. 如图,在平行四边形中,与相交于点,图中共有 个平行四边形
11. 如图,在平行四边形□中,的平分线与的平分线交于点E,若点E恰好在边上,则的值为 .
12. ?ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:________,使得?ABCD为正方形.
13. 如图,,四边形和都是矩形,则等于
14. 某台球桌为如图所示长方形,小球从沿角出击,恰好经过次碰撞到处,则=
三、解答题
15. 如图,四边形为平行四边形,即,.通过证明三角形全等来说明:
⑴,.(对边相等)
⑵,.(对角线互相平分)
16. 如图,、分别是平行四边形的、边上的点,且.
⑴求证:≌;
⑵若、分别是、的中点,连接、,试判断四边形是怎样的四边形,并证明你的结论.
17. 如图,将?ABCD的AD边延长至点E,使DE=AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
18. 如图,是矩形的对角线交点,过点作分别交、于、,若,,求四边形的面积.
人教版 八年级数学下册 第18章 平行四边形 综合训练-答案
一、选择题
1. 【答案】C
【解析】由折叠可得,∠ACD=∠ACE=90°,∴∠BAC=90°,
又∵∠B=60°,∴∠ACB=30°,∴BC=2AB=6,∴AD=6,
由折叠可得,∠E=∠D=∠B=60°,
∴∠DAE=60°,∴△ADE是等边三角形,
∴△ADE的周长为6×3=18,
故选C.
2. 【答案】D,
【解析】本题考查矩形的性质,三角形中位线定理.
解:矩形ABCD中,∵AB=6cm,∴DC=6cm,∵∠BCD=90°,BC=8cm,∴BD=10.
∵对角线AC,BD相交于点O,∴OD=BD=5.∵点E,F分别是AO,AD的中点,∴EF=2.5.故选D.
3. 【答案】A 【解析】由折叠的性质知∠EA′B′=∠A=90°,∵∠2=40°,∴∠B′A′C=50°,∴∠EA′D=40°,∠DEA′=50°,∴∠AEA′=130°,∴∠AEF=∠FEA′=∠AEA′=65°,∵AD∥BC,∴∠1=180°-65°=115°.
4. 【答案】B
【解析】本题考查了特殊四边形的判定.当点E从点A出发沿AB向点B运动时,四边形AECF的形状依次如下图所示.因此本题选B.
5. 【答案】B
【解析】由已知及菱形的性质求得∠ABD=∠CDB=30?,AO⊥BD,利用含30?的直角三角形边的关系分别求得AO、DO、OE、DE,进而求得四边形AOED的周长.∵四边形ABCD是菱形,O是对角线AC的中点,∴AO⊥BD,AD=AB=4,AB∥DC;∵∠BAD=120?,∴∠ABD=∠ADB=∠CDB=30?;∵OE⊥DC,∴在Rt△AOD中,AD=4,AO=AD=2,DO==2;在Rt△DEO中,OE=OD=,DE==3,∴四边形AOED的周长为AO+OE+DE+AD=2++3+4=9+.
6. 【答案】C
7. 【答案】C
【解析】可知四边形均为平行四边形,可知选C
8. 【答案】B 【解析】设CH=x,∵BE∶EC=2∶1,BC=9,∴EC=3,由折叠可知,EH=DH=9-x,在Rt△ECH中,由勾股定理得:(9-x)2=32+x2,解得:x=4.
二、填空题
9. 【答案】2 【解析】根据“矩形的对角线相等且互相平分”进行解题便可.∵四边形ABCD是矩形,∴BD=AC=2OA,∵OA=1,∴BD=2.
10. 【答案】个
11. 【答案】16
【解析】∵四边形ABCD是平行四边形,∴AB=CD=2,AD=BC,AD∥BC,AB∥CD,∴∠ABC+∠BCD=180°, ∠AEB=∠EBC,∠DEC=∠ECB.又∵BE、CE分别是∠ABC与∠DCB的平分线,∴∠ABE=∠EBC,∠DCE=∠ECB,∴∠EBC+∠BCE=90°,∠ABE=∠AEB,∠DCE=∠DEC,∴AB=AE=2,DC=DE=2,
12. 【答案】∠BAD=90°(答案不唯一) 【解析】∵?ABCD的对角线AC与BD相交于点O,且AC⊥BD,∴?ABCD是菱形,当∠BAD=90°时,菱形ABCD为正方形.故可添加条件:∠BAD=90°.
13. 【答案】
14. 【答案】
【解析】由图形可知:可推出
三、解答题
15. 【答案】
⑴ ∵,
∴,
在和中,
∴
∴,.
⑵ 在和中,
∴,.
16. 【答案】
⑴由是平行四边形可知,,
又,故≌
⑵由(1)可知,,
又,,∴
而∥,∴有
∴,∴∥
∴四边形为平行四边形
17. 【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥FC.(2分)
∵F是BC的中点,
∴FC=BC=AD,
∵DE=AD,∴FC=DE,(4分)
∴四边形CEDF是平行四边形.(5分)
(2)
解图
解:如解图,过点D作DH⊥BC于点H.
由(1)知四边形DECF是平行四边形,
∴DF=CE.(6分)
∵四边形ABCD是平行四边形,∠A=60°,AB=3,AD=4,
∴BC=4,CD=3,∠BCD=60°,(8分)
在Rt△DHC中,HC=DC·cos∠HCD=,
DH=DC·sin∠HCD=,
∵F是BC的中点,
∴FC=2,
∴FH=FC-HC=2-=,(10分)
在Rt△DFH中,由勾股定理得DF==
=,
∴CE=.(12分)
18. 【答案】
【解析】由为矩形可知,
又∵∥,∴
又,∴≌. 故
从而可知为菱形,∴.
又∵,
∴在直角中,由勾股定理有,
解得.故四边形的面积为()
