人教版 九年级数学下册 第27章 相似 综合训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学下册 第27章 相似 综合训练(Word版 含答案) | 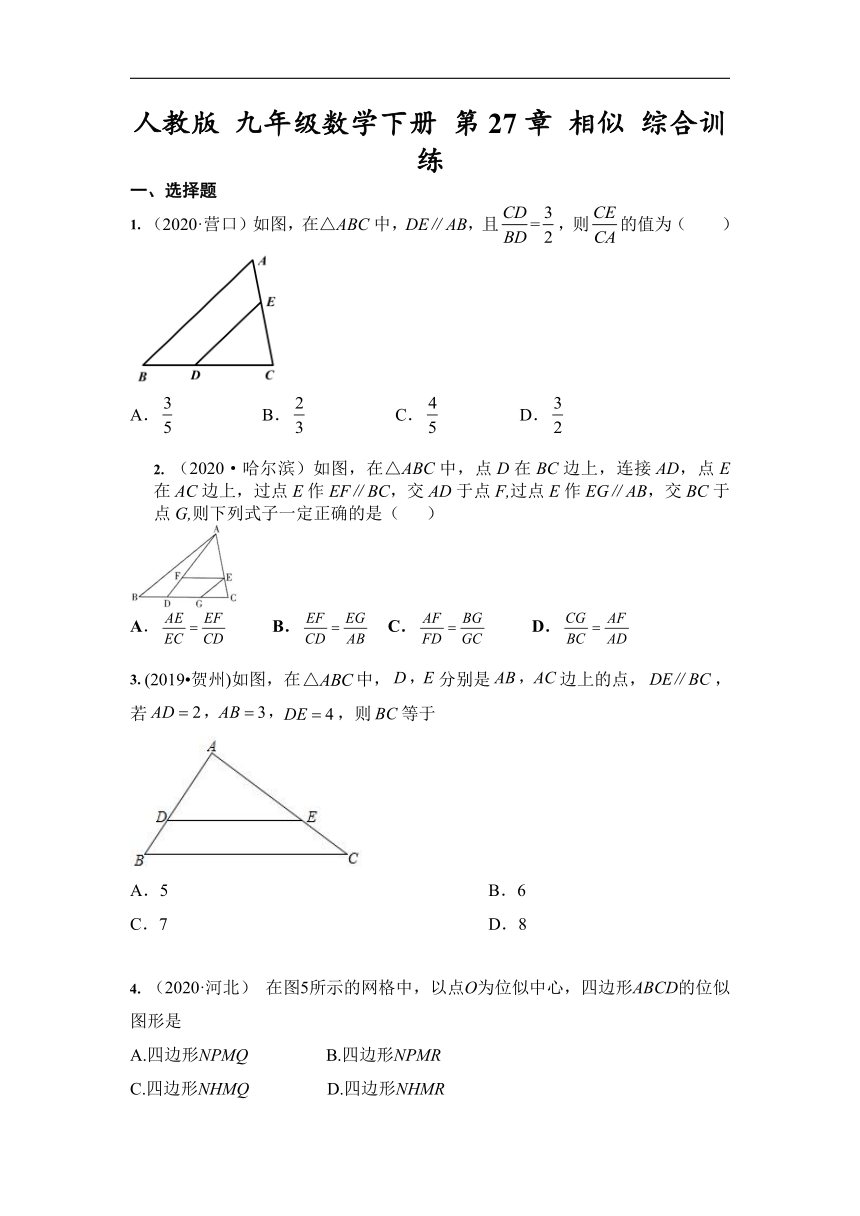 | |
| 格式 | doc | ||
| 文件大小 | 832.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 20:59:29 | ||
图片预览

文档简介
人教版 九年级数学下册 第27章 相似 综合训练
一、选择题
1. (2020·营口)如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
2. (2020·哈尔滨)如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A. B. C. D.
3. (2019?贺州)如图,在中,分别是边上的点,,若,则等于
A.5 B.6
C.7 D.8
4. (2020·河北) 在图5所示的网格中,以点O为位似中心,四边形ABCD的位似图形是
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
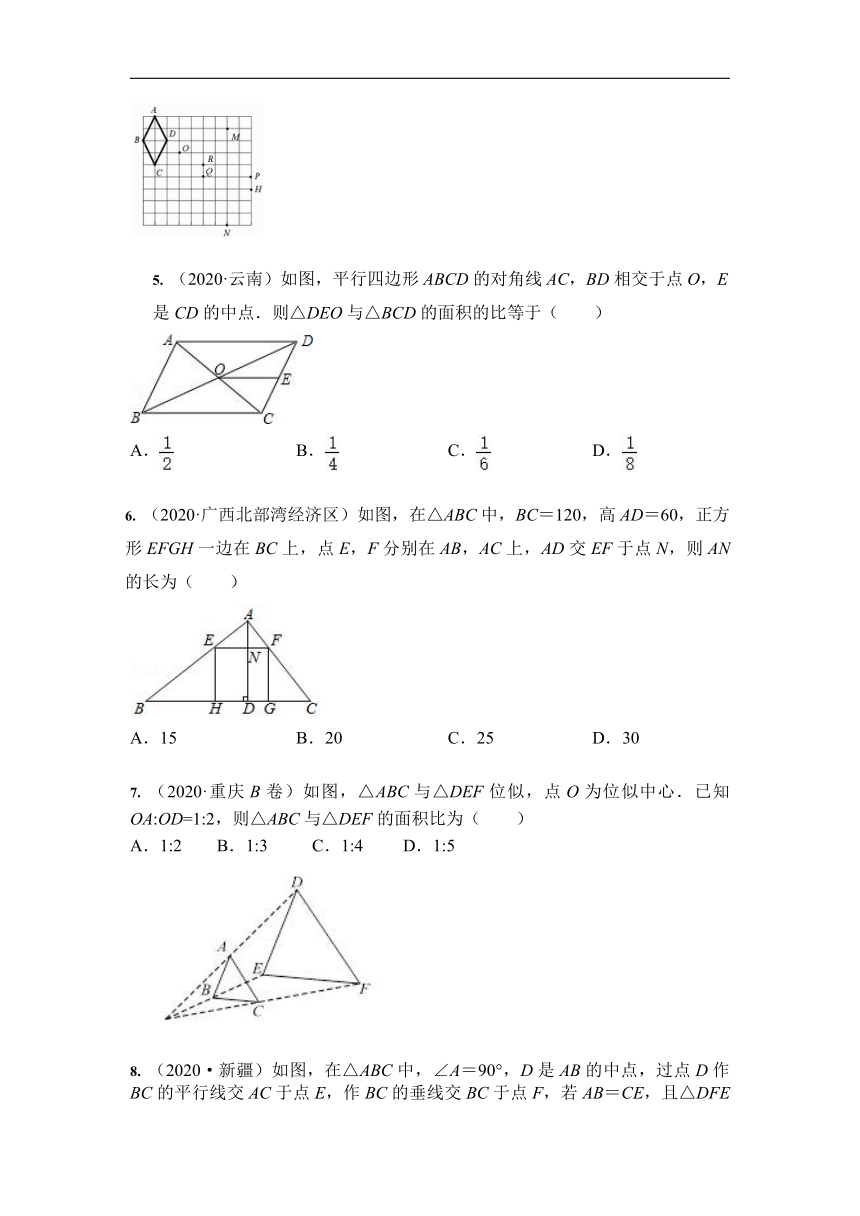
5. (2020·云南)如图,平行四边形ABCD的对角线AC,BD相交于点O,E是CD的中点.则△DEO与△BCD的面积的比等于( )
A. B. C. D.
6. (2020·广西北部湾经济区)如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15 B.20 C.25 D.30
7. (2020·重庆B卷)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
8. (2020·新疆)如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为 ( )
A. B.5 C. D.10
二、填空题
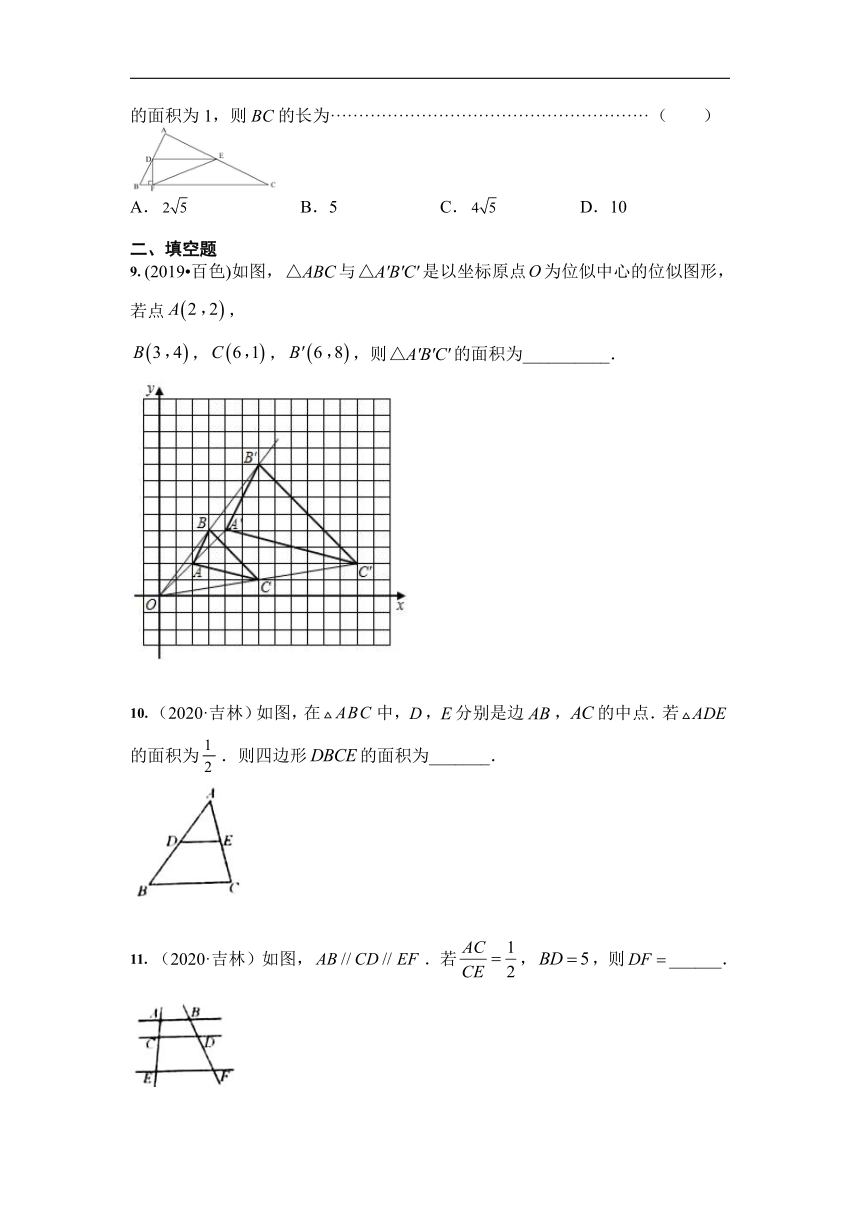
9. (2019?百色)如图,与是以坐标原点为位似中心的位似图形,若点,
,,,则的面积为__________.
10. (2020·吉林)如图,在中,,分别是边,的中点.若的面积为.则四边形的面积为_______.
11. (2020·吉林)如图,.若,,则______.
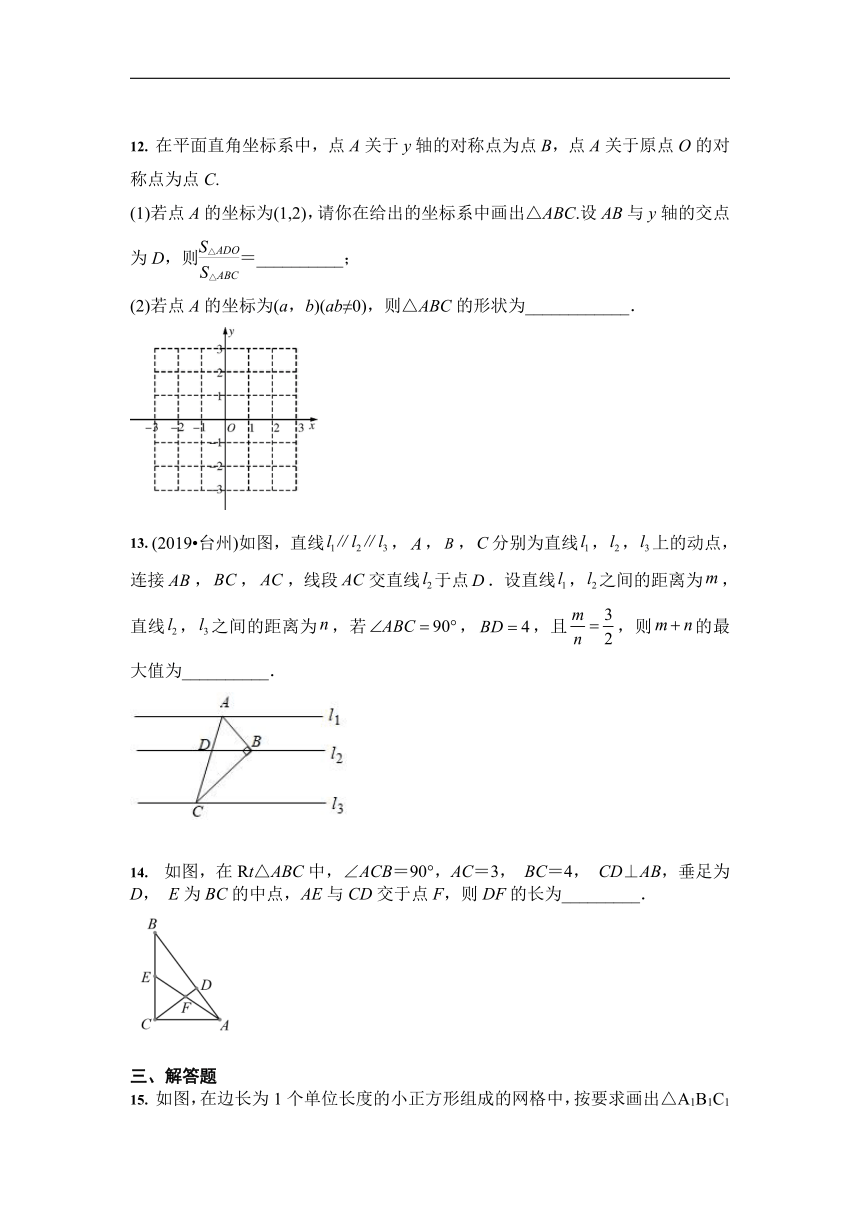
12. 在平面直角坐标系中,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出△ABC.设AB与y轴的交点为D,则=__________;
(2)若点A的坐标为(a,b)(ab≠0),则△ABC的形状为____________.
13. (2019?台州)如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为__________.
14. 如图,在Rt△ABC中,∠ACB=90°,AC=3, BC=4, CD⊥AB,垂足为D, E为BC的中点,AE与CD交于点F,则DF的长为_________.
三、解答题
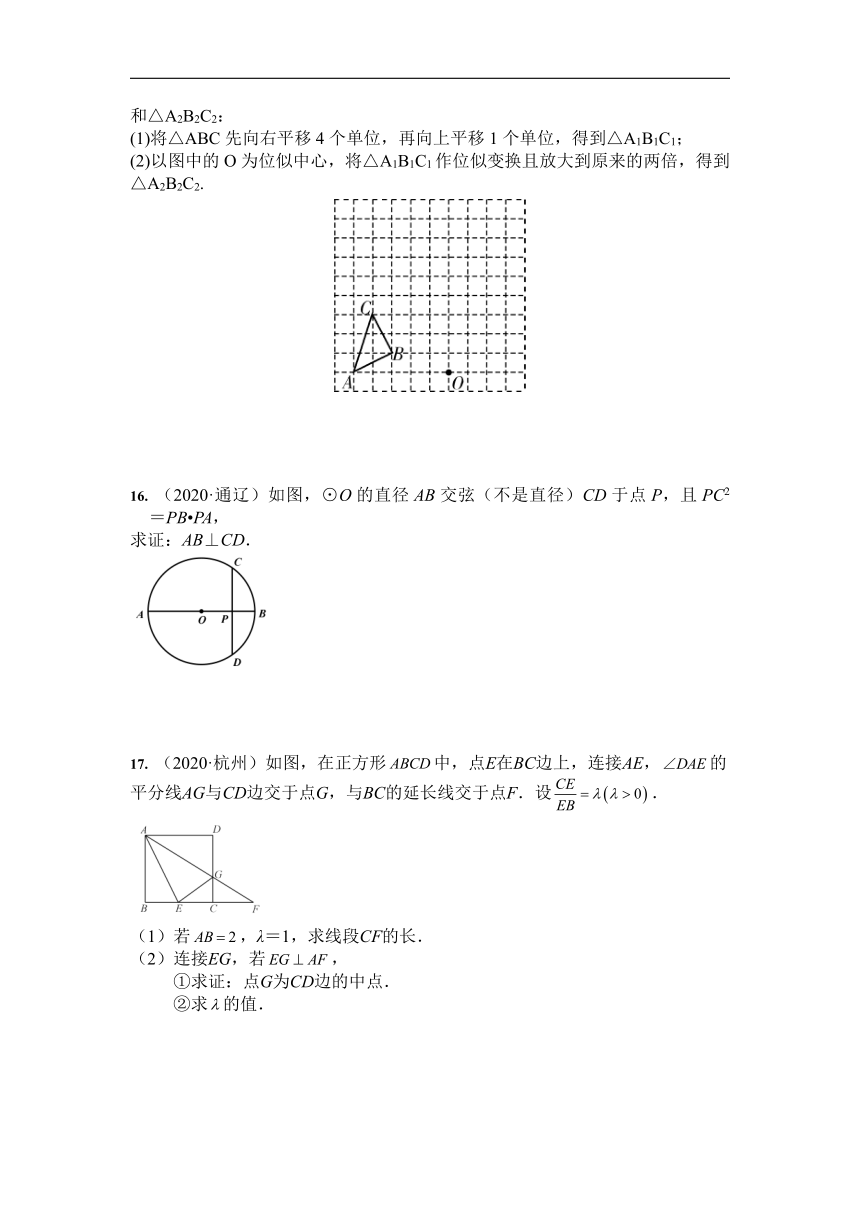
15. 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
(1)将△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
16. (2020·通辽)如图,⊙O的直径AB交弦(不是直径)CD于点P,且PC2=PB?PA,
求证:AB⊥CD.
17. (2020·杭州)如图,在正方形中,点E在BC边上,连接AE,的平分线AG与CD边交于点G,与BC的延长线交于点F.设.
(1)若,λ=1,求线段CF的长.
(2)连接EG,若,
①求证:点G为CD边的中点.
②求的值.
18. (2020·南京)如图,在△ABC和△A’B’C’中,D、D’分别是AB、A’B’上一点,=.
(1)当==时,求证:△ABC∽△A’B’C’.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A’B’C’是否相似,并说明理由.
人教版 九年级数学下册 第27章 相似 综合训练-答案
一、选择题
1. 【答案】A
【解析】利用平行截割定理求的值.∵DE∥AB,∴==,∵CE+AE=AC,∴=.
2. 【答案】C【解析】本题考查了平行线分线段成比例和由平行判定相似,∵EF∥BC,∴,∵EF∥BC,∴,∴因此本题选C.
3. 【答案】B
【解析】∵,∴,
∴,即,解得:,故选B.
4. 【答案】A
【解析】解析:连接AO并延长AO至点N,连接BO并延长PO至点P, 连接CO并延长CO至点M, 连接DO并延长DO至Q,可知,所以以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故答案为A.
5. 【答案】 B.
【解析】利用平行四边形的性质可得出点O为线段BD的中点,结合点E是CD的中点可得出线段OE为△DBC的中位线,利用三角形中位线定理可得出OE∥BC,OE=BC,进而可得出△DOE∽△DBC,再利用相似三角形的面积比等于相似比的平分,即可求出△DEO与△BCD的面积的比为1:4.
6. 【答案】 B
【解析】设正方形EFGH的边长EF=EH=x,
∵四边EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,
∴△AEF∽△ABC,
∵AD是△ABC的高,
∴∠HDN=90°,
∴四边形EHDN是矩形,
∴DN=EH=x,
∵△AEF∽△ABC,
∴(相似三角形对应边上的高的比等于相似比),
∵BC=120,AD=60,
∴AN=60﹣x,
∴,
解得:x=40,
∴AN=60﹣x=60﹣40=20.因此本题选B.
7. 【答案】C
【解析】本题考查了相似三角形的性质, ∵△ABC与△DEF位似,且,∴,因此本题选C.
8. 【答案】A
【解析】本题考查了相似三角形的判定与性质,三角形的中位线定理.如答图,过点E作EG⊥BC于G,过点A作AH⊥BC于H.
又因为DF⊥BC,所以DF∥AH∥EG,四边形DEGF是矩形.所以△BDF∽△BAH,DF=EG,所以=,因为D为AB中点,所以=,所以=.设DF=EG=x,则AH=2x.因为∠BAC=90°,所以∠B+∠C=90°,因为EG⊥BC,所以∠C+∠CEG=90°,所以∠B=∠CEG,又因为∠BHA=∠CGE=90°,AB=CE,所以△ABH≌△CEG,所以CG=AH=2x.同理可证△BDF∽△ECG,所以=,因为BD=AB=CE,所以=EG=x.在Rt△BDF中,由勾股定理得BD===x,所以AD=x,所以CE=AB=2AD=x.因为DE∥BC,所以==,所以AE=AC=CE=x.
在Rt△ADE中,由勾股定理得DE===x.因△DEF的面积为1,所以DE·DF=1,即×x·x=1,解得x=,所以DE=×=,因为AD=BD,AE=CE,所以BC=2DE=,因此本题选D.
二、填空题
9. 【答案】18
【解析】∵与是以坐标原点为位似中心的位似图形,
若点,,∴位似比为,
∵,,
∴,
∴的面积为:,
故答案为:18.
10. 【答案】
【解析】点,分别是边,的中点,
,即
又,
则四边形的面积为.
故答案为:.
11. 【答案】10
【解析】∵,∴,
又∵,,∴,∴,故答案为:10.
12. 【答案】(1)△ABC如图 (2)直角三角形 解析:(1)因为点A的坐标为(1,2),所以点A关于y轴的对称点B的坐标为(-1,2),关于原点的对称点C的坐标为(-1,-2).连AB,BC,AC,作△ABC.
设AB交y轴于D点,如图,
D点坐标为(0,2),
∵OD∥BC,
∴△ADO∽△ABC.
∴==.
(2)∵ab≠0,∴a≠0,且b≠0,
∴点A不在坐标轴上,
∴AB∥x轴,BC⊥x轴.
∴∠ABC=90°.
∴△ABC是直角三角形.
13. 【答案】
【解析】如图,过作于,延长交于,过作于,过作于,
设,,,,
∵,∴,,
∵,
∴,
∴,∴,
∴,即,∴,
∵,∴,
∴,即,
∴,
∵,∴,
∴,
∴当最大时,,
∵,
∴当时,,
∴,
∴的最大值为.故答案为:.
14. 【答案】
【解析】本题考查平行线分线段成比例定理,相似三角形的判定与性质.已知∠ACB=90°,AC=3, BC=4,由勾股定理,得AB=5.CD⊥AB,由三角形的面积,得CD==.易得△ABC∽△ACD∽△CBD,由相似三角形对应边成比例,得AD==,BD==.过点E作EG∥AB交CD于点G,由平行线分线段成比例,得DG=CD=,EG=,所以,即,所以DF=,故答案为.
三、解答题
15. 【答案】
解:(1)正确图形如解图.
(2)正确图形如解图.
解图
16. 【答案】
解:如图,连结AC,BD.∵∠A=∠D,∠C=∠B,∴△ACP∽△DBP,∴=,∴PC?PD=PB?PA,∵PC2=PB?PA,∴PC=PD,即AB平分CD,∵CD是弦(不是直径),AB是直径,∴AB⊥CD.
17. 【答案】
解:(1)∵四边形ABCD是正方形,∴AD∥BC,AB=BC=2,∴∠DAF=∠F.∵AG平分∠DAE,∴∠DAF=∠EAF,∴∠EAF=∠F,∴EA=EF.∵λ=1,∴BE=EC=1.在Rt△ABE中,由勾股定理得EA=,∴CF=EF-EC=-1.
(2)①∵EA=EF,EG⊥AF,∴AG=GF.又∵∠AGD=∠FGC,∠DAG=∠F,所以△DAG≌△CFG,∴DG=CG,∴点G为CD边的中点.
②不妨设CD=2,则CG=1.由①知CF=AD=2.∵EG⊥AF,∴∠EGF=90°.∵四边形ABCD是正方形,∴∠BCD=90°,∴∠BCD=∠FCG,∠EGC+∠CGF=90°,∠EGC+∠GEC=90°,∴∠CGF=∠GEC,∴△EGC∽△GFC,∴==,∴EC=,∴BE=,∴λ=.
18. 【答案】
解:(1) == ∠A=∠A’.
(2)如图,过点D、D’分别作DE∥BC,D’E’∥B’C’,DE交AC于点E,D’E’交A’C’于点E’.
∵DE∥BC,
∴△ADE∽△ABC.
∴==.
同理==.
又=,
∴=,
∴=.
同理 =.
∴=,即=.
∴=.
又==,
∴==,
∴△DCE∽△D’C’E’.
∴∠CED=∠C’E’D’.
∵DE∥BC,
∴∠CED+∠ACB=180°.
同理 ∠C’E’D’+∠A’C’B’=180°.
∴∠ACB=∠A’C’B’.
又=
∴△ABC∽△A’B’C’.
一、选择题
1. (2020·营口)如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
2. (2020·哈尔滨)如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A. B. C. D.
3. (2019?贺州)如图,在中,分别是边上的点,,若,则等于
A.5 B.6
C.7 D.8
4. (2020·河北) 在图5所示的网格中,以点O为位似中心,四边形ABCD的位似图形是
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
5. (2020·云南)如图,平行四边形ABCD的对角线AC,BD相交于点O,E是CD的中点.则△DEO与△BCD的面积的比等于( )
A. B. C. D.
6. (2020·广西北部湾经济区)如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为( )
A.15 B.20 C.25 D.30
7. (2020·重庆B卷)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
8. (2020·新疆)如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为 ( )
A. B.5 C. D.10
二、填空题
9. (2019?百色)如图,与是以坐标原点为位似中心的位似图形,若点,
,,,则的面积为__________.
10. (2020·吉林)如图,在中,,分别是边,的中点.若的面积为.则四边形的面积为_______.
11. (2020·吉林)如图,.若,,则______.
12. 在平面直角坐标系中,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出△ABC.设AB与y轴的交点为D,则=__________;
(2)若点A的坐标为(a,b)(ab≠0),则△ABC的形状为____________.
13. (2019?台州)如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为__________.
14. 如图,在Rt△ABC中,∠ACB=90°,AC=3, BC=4, CD⊥AB,垂足为D, E为BC的中点,AE与CD交于点F,则DF的长为_________.
三、解答题
15. 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
(1)将△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
16. (2020·通辽)如图,⊙O的直径AB交弦(不是直径)CD于点P,且PC2=PB?PA,
求证:AB⊥CD.
17. (2020·杭州)如图,在正方形中,点E在BC边上,连接AE,的平分线AG与CD边交于点G,与BC的延长线交于点F.设.
(1)若,λ=1,求线段CF的长.
(2)连接EG,若,
①求证:点G为CD边的中点.
②求的值.
18. (2020·南京)如图,在△ABC和△A’B’C’中,D、D’分别是AB、A’B’上一点,=.
(1)当==时,求证:△ABC∽△A’B’C’.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A’B’C’是否相似,并说明理由.
人教版 九年级数学下册 第27章 相似 综合训练-答案
一、选择题
1. 【答案】A
【解析】利用平行截割定理求的值.∵DE∥AB,∴==,∵CE+AE=AC,∴=.
2. 【答案】C【解析】本题考查了平行线分线段成比例和由平行判定相似,∵EF∥BC,∴,∵EF∥BC,∴,∴因此本题选C.
3. 【答案】B
【解析】∵,∴,
∴,即,解得:,故选B.
4. 【答案】A
【解析】解析:连接AO并延长AO至点N,连接BO并延长PO至点P, 连接CO并延长CO至点M, 连接DO并延长DO至Q,可知,所以以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故答案为A.
5. 【答案】 B.
【解析】利用平行四边形的性质可得出点O为线段BD的中点,结合点E是CD的中点可得出线段OE为△DBC的中位线,利用三角形中位线定理可得出OE∥BC,OE=BC,进而可得出△DOE∽△DBC,再利用相似三角形的面积比等于相似比的平分,即可求出△DEO与△BCD的面积的比为1:4.
6. 【答案】 B
【解析】设正方形EFGH的边长EF=EH=x,
∵四边EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,
∴△AEF∽△ABC,
∵AD是△ABC的高,
∴∠HDN=90°,
∴四边形EHDN是矩形,
∴DN=EH=x,
∵△AEF∽△ABC,
∴(相似三角形对应边上的高的比等于相似比),
∵BC=120,AD=60,
∴AN=60﹣x,
∴,
解得:x=40,
∴AN=60﹣x=60﹣40=20.因此本题选B.
7. 【答案】C
【解析】本题考查了相似三角形的性质, ∵△ABC与△DEF位似,且,∴,因此本题选C.
8. 【答案】A
【解析】本题考查了相似三角形的判定与性质,三角形的中位线定理.如答图,过点E作EG⊥BC于G,过点A作AH⊥BC于H.
又因为DF⊥BC,所以DF∥AH∥EG,四边形DEGF是矩形.所以△BDF∽△BAH,DF=EG,所以=,因为D为AB中点,所以=,所以=.设DF=EG=x,则AH=2x.因为∠BAC=90°,所以∠B+∠C=90°,因为EG⊥BC,所以∠C+∠CEG=90°,所以∠B=∠CEG,又因为∠BHA=∠CGE=90°,AB=CE,所以△ABH≌△CEG,所以CG=AH=2x.同理可证△BDF∽△ECG,所以=,因为BD=AB=CE,所以=EG=x.在Rt△BDF中,由勾股定理得BD===x,所以AD=x,所以CE=AB=2AD=x.因为DE∥BC,所以==,所以AE=AC=CE=x.
在Rt△ADE中,由勾股定理得DE===x.因△DEF的面积为1,所以DE·DF=1,即×x·x=1,解得x=,所以DE=×=,因为AD=BD,AE=CE,所以BC=2DE=,因此本题选D.
二、填空题
9. 【答案】18
【解析】∵与是以坐标原点为位似中心的位似图形,
若点,,∴位似比为,
∵,,
∴,
∴的面积为:,
故答案为:18.
10. 【答案】
【解析】点,分别是边,的中点,
,即
又,
则四边形的面积为.
故答案为:.
11. 【答案】10
【解析】∵,∴,
又∵,,∴,∴,故答案为:10.
12. 【答案】(1)△ABC如图 (2)直角三角形 解析:(1)因为点A的坐标为(1,2),所以点A关于y轴的对称点B的坐标为(-1,2),关于原点的对称点C的坐标为(-1,-2).连AB,BC,AC,作△ABC.
设AB交y轴于D点,如图,
D点坐标为(0,2),
∵OD∥BC,
∴△ADO∽△ABC.
∴==.
(2)∵ab≠0,∴a≠0,且b≠0,
∴点A不在坐标轴上,
∴AB∥x轴,BC⊥x轴.
∴∠ABC=90°.
∴△ABC是直角三角形.
13. 【答案】
【解析】如图,过作于,延长交于,过作于,过作于,
设,,,,
∵,∴,,
∵,
∴,
∴,∴,
∴,即,∴,
∵,∴,
∴,即,
∴,
∵,∴,
∴,
∴当最大时,,
∵,
∴当时,,
∴,
∴的最大值为.故答案为:.
14. 【答案】
【解析】本题考查平行线分线段成比例定理,相似三角形的判定与性质.已知∠ACB=90°,AC=3, BC=4,由勾股定理,得AB=5.CD⊥AB,由三角形的面积,得CD==.易得△ABC∽△ACD∽△CBD,由相似三角形对应边成比例,得AD==,BD==.过点E作EG∥AB交CD于点G,由平行线分线段成比例,得DG=CD=,EG=,所以,即,所以DF=,故答案为.
三、解答题
15. 【答案】
解:(1)正确图形如解图.
(2)正确图形如解图.
解图
16. 【答案】
解:如图,连结AC,BD.∵∠A=∠D,∠C=∠B,∴△ACP∽△DBP,∴=,∴PC?PD=PB?PA,∵PC2=PB?PA,∴PC=PD,即AB平分CD,∵CD是弦(不是直径),AB是直径,∴AB⊥CD.
17. 【答案】
解:(1)∵四边形ABCD是正方形,∴AD∥BC,AB=BC=2,∴∠DAF=∠F.∵AG平分∠DAE,∴∠DAF=∠EAF,∴∠EAF=∠F,∴EA=EF.∵λ=1,∴BE=EC=1.在Rt△ABE中,由勾股定理得EA=,∴CF=EF-EC=-1.
(2)①∵EA=EF,EG⊥AF,∴AG=GF.又∵∠AGD=∠FGC,∠DAG=∠F,所以△DAG≌△CFG,∴DG=CG,∴点G为CD边的中点.
②不妨设CD=2,则CG=1.由①知CF=AD=2.∵EG⊥AF,∴∠EGF=90°.∵四边形ABCD是正方形,∴∠BCD=90°,∴∠BCD=∠FCG,∠EGC+∠CGF=90°,∠EGC+∠GEC=90°,∴∠CGF=∠GEC,∴△EGC∽△GFC,∴==,∴EC=,∴BE=,∴λ=.
18. 【答案】
解:(1) == ∠A=∠A’.
(2)如图,过点D、D’分别作DE∥BC,D’E’∥B’C’,DE交AC于点E,D’E’交A’C’于点E’.
∵DE∥BC,
∴△ADE∽△ABC.
∴==.
同理==.
又=,
∴=,
∴=.
同理 =.
∴=,即=.
∴=.
又==,
∴==,
∴△DCE∽△D’C’E’.
∴∠CED=∠C’E’D’.
∵DE∥BC,
∴∠CED+∠ACB=180°.
同理 ∠C’E’D’+∠A’C’B’=180°.
∴∠ACB=∠A’C’B’.
又=
∴△ABC∽△A’B’C’.
