人教版七年级下册数学 5.3.1平行线的性质 同步测试 (Word版 含答案)
文档属性
| 名称 | 人教版七年级下册数学 5.3.1平行线的性质 同步测试 (Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 104.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 21:06:19 | ||
图片预览



文档简介
5.3.1平行线的性质 同步测试
一.选择题
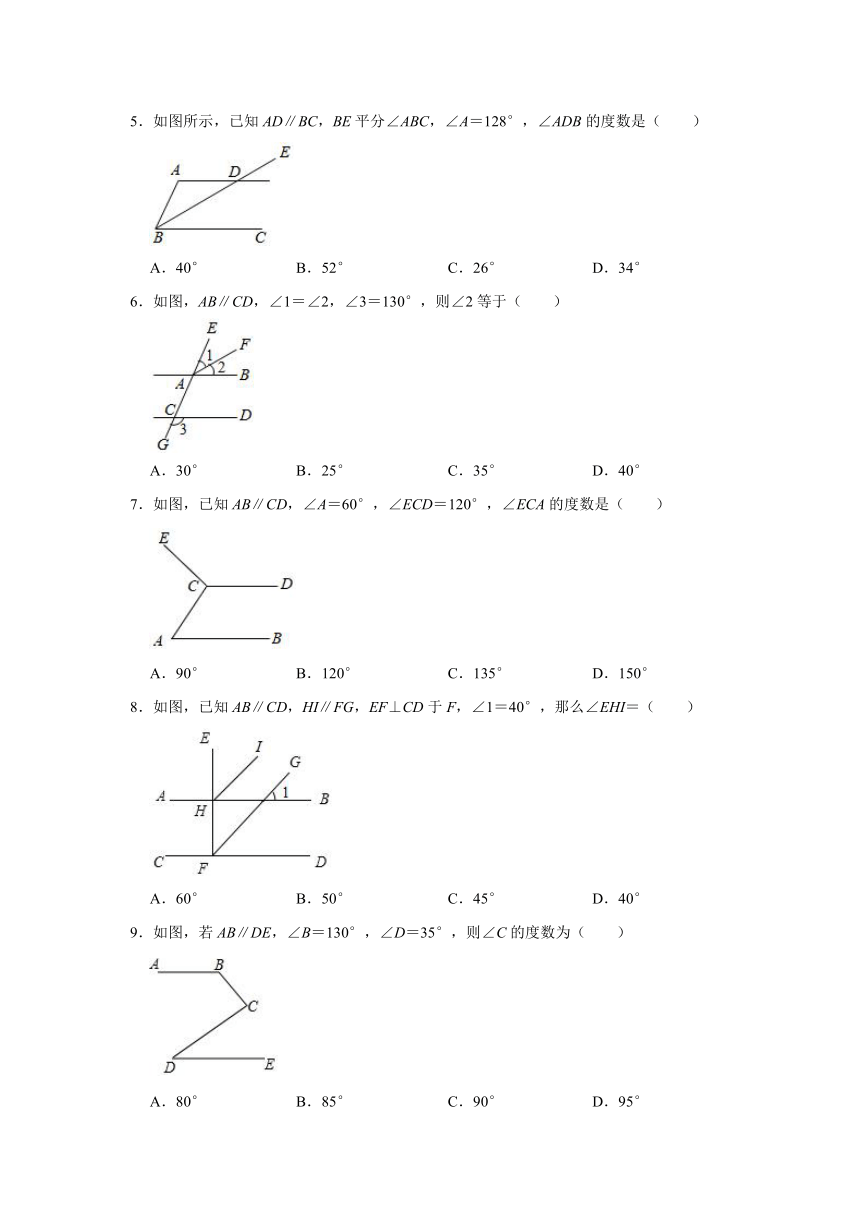
1.下列四个图形中,不能推出∠2与∠1相等的是( )
A. B.
C. D.
2.如图,已知AC∥DE,∠B=50°,∠C=20°,则∠E的度数是( )
A.40° B.50° C.60° D.70°
3.如图所示,已知AB∥CD,则( )
A.∠1=∠2+∠3 B.∠1>∠2+∠3 C.∠2=∠1+∠3 D.∠1<∠2+∠3
4.如图,AB∥CD,BF平分∠ABE,且BF⊥DE垂足为F,则∠ABE与∠EDC的数量关系是( )
A.∠ABE=∠EDC B.∠ABE+∠EDC=180°
C.∠EDC﹣∠ABE=90° D.∠ABE+∠EDC=90°
5.如图所示,已知AD∥BC,BE平分∠ABC,∠A=128°,∠ADB的度数是( )
A.40° B.52° C.26° D.34°
6.如图,AB∥CD,∠1=∠2,∠3=130°,则∠2等于( )
A.30° B.25° C.35° D.40°
7.如图,已知AB∥CD,∠A=60°,∠ECD=120°,∠ECA的度数是( )
A.90° B.120° C.135° D.150°
8.如图,已知AB∥CD,HI∥FG,EF⊥CD于F,∠1=40°,那么∠EHI=( )
A.60° B.50° C.45° D.40°
9.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80° B.85° C.90° D.95°
10.如图,下列命题:①若∠1=∠2,则∠D=∠4;②若∠C=∠D,则∠4=∠C;③若∠A=
∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则∠A=∠F;⑤若∠C=∠D,∠A=∠F,则∠1=∠2.其中正确的个数有( )个.
A.1 B.2 C.3 D.4
二.填空题
11.如图,AB∥CD,∠A=75°,∠C=30°,∠E的度数为 .
12.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A= .
13.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=57°,则∠2的度数是 .
14.如图,已知AB∥CD,BE平分∠ABD,∠BED=25°,则∠D= °.
15.如图,AB∥CD,CE交AB于F,∠C=55°,∠AEC=18°,则∠A= °.
三.解答题
16.已知:如图,在△ABC中,CD⊥AB于点D,G是BC上一点,过点G作GF⊥AB于点F,且满足∠B=∠ADE.求证:∠CDE=∠BGF.
17.补全证明过程:(括号内填写理由)
一条直线分别与直线BE、直线CE、直线BF、直线CF相交于A、G、H、D,如果∠1=∠2,∠A=∠D,求证:∠B=∠C.
证明:∵∠1=∠2(已知),∠1=∠3,( )
∴∠2=∠3,( )
∴CE∥BF,( )
∴∠C=∠4,( )
又∵∠A=∠D,( )
∴AB∥ ,( )
∴∠B=∠4,( )
∴∠B=∠C.(等量代换)
18.如图(1),直线AB、CD被直线EF所截,AB∥CD,EG平分∠AEF,FG平分∠CFE.
(1)试判断EG与GF的位置关系;
(2)过点G作直线m∥AB(如图(2)),点P为直线m上一点,当∠EPF=80°时,求∠AEP+∠CFP的度数.
参考答案
1.D
2.D
3.A
4.C
5.C
B
7.B
8.B
9.B
10.C
11.45°
12.50°
13.33.
14.130
15.37
16.证明:∵CD⊥AB,GF⊥AB,
∴FG∥CD,
∴∠FGB=∠DCB,
∵∠B=∠ADE,
∴DE∥BC,
∴∠EDC=∠DCG,
∴∠CDE=∠BGF.
17.证明:∵∠1=∠2(已知),∠1=∠3(对顶角相等),
∴∠2=∠3(等量代换),
∴CE∥BF(同位角相等,两直线平行),
∴∠C=∠4(两直线平行,同位角相等),
又∵∠A=∠D(已知),
∴AB∥CD(内错角相等,两直线平行),
∴∠B=∠4(两直线平行,内错角相等),
∴∠B=∠C(等量代换).
答案:对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;已知;CD;内错角相等,两直线平行;两直线平行,内错角相等.
18.(1)EG⊥GF,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵EG平分∠AEF,FG平分∠CFE,
∴∠AEF=2∠GEF,∠CFE=2∠GFE,
∴∠EGF+∠GFE=90°,
∴EG⊥GF;
(2)
分为两种情况:①如图(1),
∵PG∥AB,AB∥CD,
∴PG∥AB∥CD,
∴∠AEP=∠EPG,∠CFP=∠FPG,
∵∠EPF=∠EPG+∠FPG=80°,
∴∠AEP+∠CFF=80°;
②如图(2),
∵PG∥AB,AB∥CD,
∴PG∥AB∥CD,
∴∠AEP+∠EPG=180°,∠CFP+∠FPG=180°,
∵∠EPF=∠EPG+∠FPG=80°,
∴∠AEP+∠CFP=180°+180°﹣80°=280°.
一.选择题
1.下列四个图形中,不能推出∠2与∠1相等的是( )
A. B.
C. D.
2.如图,已知AC∥DE,∠B=50°,∠C=20°,则∠E的度数是( )
A.40° B.50° C.60° D.70°
3.如图所示,已知AB∥CD,则( )
A.∠1=∠2+∠3 B.∠1>∠2+∠3 C.∠2=∠1+∠3 D.∠1<∠2+∠3
4.如图,AB∥CD,BF平分∠ABE,且BF⊥DE垂足为F,则∠ABE与∠EDC的数量关系是( )
A.∠ABE=∠EDC B.∠ABE+∠EDC=180°
C.∠EDC﹣∠ABE=90° D.∠ABE+∠EDC=90°
5.如图所示,已知AD∥BC,BE平分∠ABC,∠A=128°,∠ADB的度数是( )
A.40° B.52° C.26° D.34°
6.如图,AB∥CD,∠1=∠2,∠3=130°,则∠2等于( )
A.30° B.25° C.35° D.40°
7.如图,已知AB∥CD,∠A=60°,∠ECD=120°,∠ECA的度数是( )
A.90° B.120° C.135° D.150°
8.如图,已知AB∥CD,HI∥FG,EF⊥CD于F,∠1=40°,那么∠EHI=( )
A.60° B.50° C.45° D.40°
9.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80° B.85° C.90° D.95°
10.如图,下列命题:①若∠1=∠2,则∠D=∠4;②若∠C=∠D,则∠4=∠C;③若∠A=
∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则∠A=∠F;⑤若∠C=∠D,∠A=∠F,则∠1=∠2.其中正确的个数有( )个.
A.1 B.2 C.3 D.4
二.填空题
11.如图,AB∥CD,∠A=75°,∠C=30°,∠E的度数为 .
12.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A= .
13.如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=57°,则∠2的度数是 .
14.如图,已知AB∥CD,BE平分∠ABD,∠BED=25°,则∠D= °.
15.如图,AB∥CD,CE交AB于F,∠C=55°,∠AEC=18°,则∠A= °.
三.解答题
16.已知:如图,在△ABC中,CD⊥AB于点D,G是BC上一点,过点G作GF⊥AB于点F,且满足∠B=∠ADE.求证:∠CDE=∠BGF.
17.补全证明过程:(括号内填写理由)
一条直线分别与直线BE、直线CE、直线BF、直线CF相交于A、G、H、D,如果∠1=∠2,∠A=∠D,求证:∠B=∠C.
证明:∵∠1=∠2(已知),∠1=∠3,( )
∴∠2=∠3,( )
∴CE∥BF,( )
∴∠C=∠4,( )
又∵∠A=∠D,( )
∴AB∥ ,( )
∴∠B=∠4,( )
∴∠B=∠C.(等量代换)
18.如图(1),直线AB、CD被直线EF所截,AB∥CD,EG平分∠AEF,FG平分∠CFE.
(1)试判断EG与GF的位置关系;
(2)过点G作直线m∥AB(如图(2)),点P为直线m上一点,当∠EPF=80°时,求∠AEP+∠CFP的度数.
参考答案
1.D
2.D
3.A
4.C
5.C
B
7.B
8.B
9.B
10.C
11.45°
12.50°
13.33.
14.130
15.37
16.证明:∵CD⊥AB,GF⊥AB,
∴FG∥CD,
∴∠FGB=∠DCB,
∵∠B=∠ADE,
∴DE∥BC,
∴∠EDC=∠DCG,
∴∠CDE=∠BGF.
17.证明:∵∠1=∠2(已知),∠1=∠3(对顶角相等),
∴∠2=∠3(等量代换),
∴CE∥BF(同位角相等,两直线平行),
∴∠C=∠4(两直线平行,同位角相等),
又∵∠A=∠D(已知),
∴AB∥CD(内错角相等,两直线平行),
∴∠B=∠4(两直线平行,内错角相等),
∴∠B=∠C(等量代换).
答案:对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;已知;CD;内错角相等,两直线平行;两直线平行,内错角相等.
18.(1)EG⊥GF,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵EG平分∠AEF,FG平分∠CFE,
∴∠AEF=2∠GEF,∠CFE=2∠GFE,
∴∠EGF+∠GFE=90°,
∴EG⊥GF;
(2)
分为两种情况:①如图(1),
∵PG∥AB,AB∥CD,
∴PG∥AB∥CD,
∴∠AEP=∠EPG,∠CFP=∠FPG,
∵∠EPF=∠EPG+∠FPG=80°,
∴∠AEP+∠CFF=80°;
②如图(2),
∵PG∥AB,AB∥CD,
∴PG∥AB∥CD,
∴∠AEP+∠EPG=180°,∠CFP+∠FPG=180°,
∵∠EPF=∠EPG+∠FPG=80°,
∴∠AEP+∠CFP=180°+180°﹣80°=280°.
