5.3 第1课时 平行线的性质-人教版七年级数学下册同步练习(Word版 含答案)
文档属性
| 名称 | 5.3 第1课时 平行线的性质-人教版七年级数学下册同步练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 21:29:28 | ||
图片预览

文档简介
5.3 平行线的性质
第1课时
平行线的性质
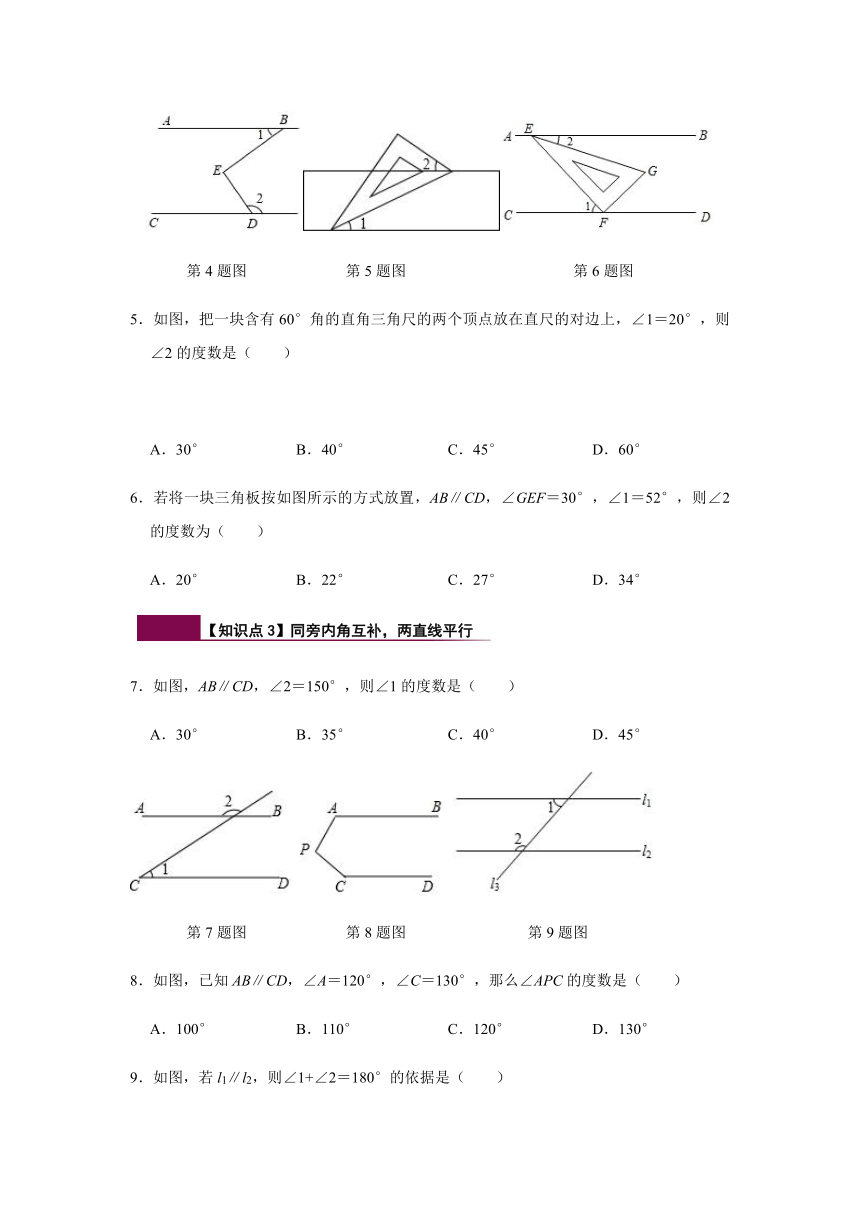
1.如图,直线l与直线a、b相交,且a∥b,∠1=50°,则∠2的度数是( )
A.130°
B.50°
C.100°
D.120°
第1题图
第2题图
第3题图
2.如图,若AB∥CD,∠1=80°,则∠2的度数为( )
A.60°
B.80°
C.100°
D.120°
3.如图,AB∥CD,∠A=75°,∠C=30°,∠E的度数为
.
4.如图,已知AB∥CD,∠BED=90°,则∠1与∠2之间的数量关系可表示为( )
A.∠2=2∠1
B.∠2﹣∠1=90°
C.∠1+∠2=180°
D.无法表示
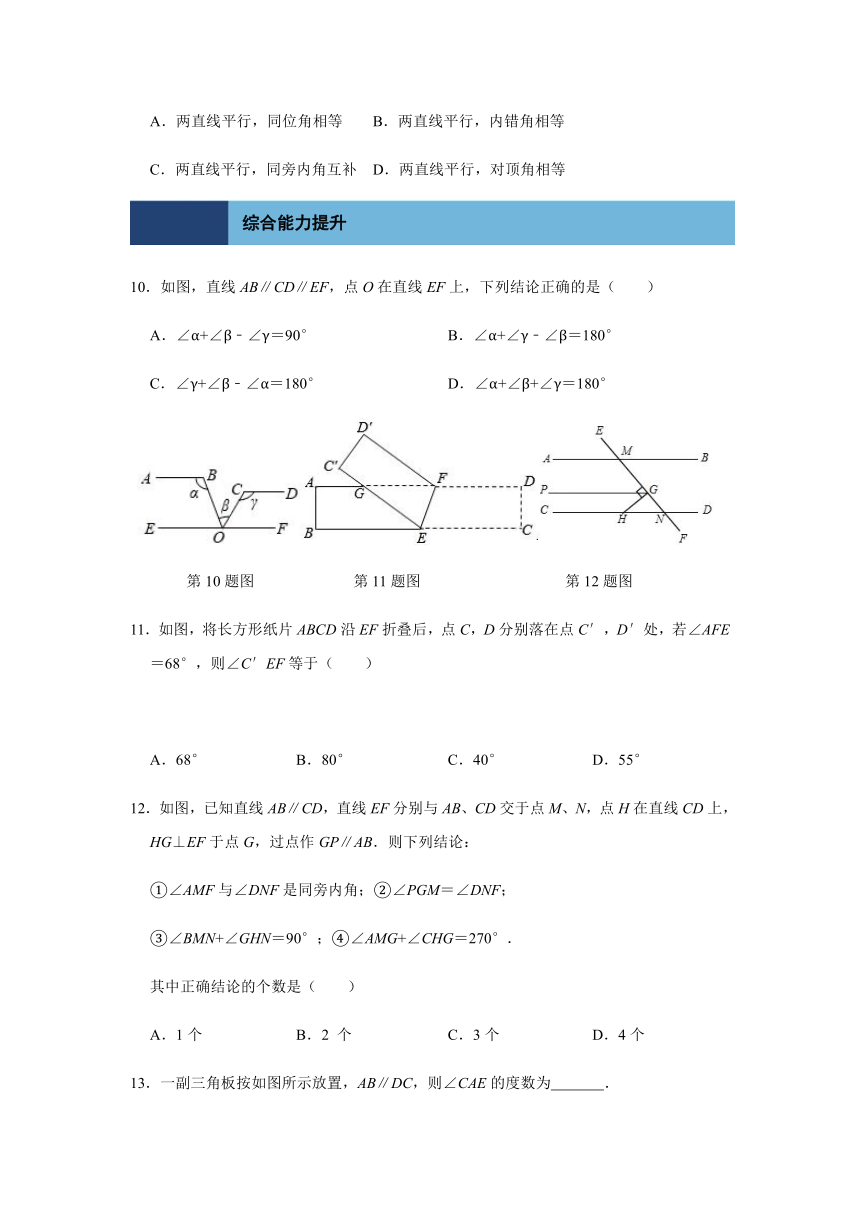
第4题图
第5题图
第6题图
5.如图,把一块含有60°角的直角三角尺的两个顶点放在直尺的对边上,∠1=20°,则∠2的度数是( )
A.30°
B.40°
C.45°
D.60°
6.若将一块三角板按如图所示的方式放置,AB∥CD,∠GEF=30°,∠1=52°,则∠2的度数为( )
A.20°
B.22°
C.27°
D.34°
7.如图,AB∥CD,∠2=150°,则∠1的度数是( )
A.30°
B.35°
C.40°
D.45°
第7题图
第8题图
第9题图
8.如图,已知AB∥CD,∠A=120°,∠C=130°,那么∠APC的度数是( )
A.100°
B.110°
C.120°
D.130°
9.如图,若l1∥l2,则∠1+∠2=180°的依据是( )
A.两直线平行,同位角相等
B.两直线平行,内错角相等
C.两直线平行,同旁内角互补
D.两直线平行,对顶角相等
10.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90°
B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180°
D.∠α+∠β+∠γ=180°
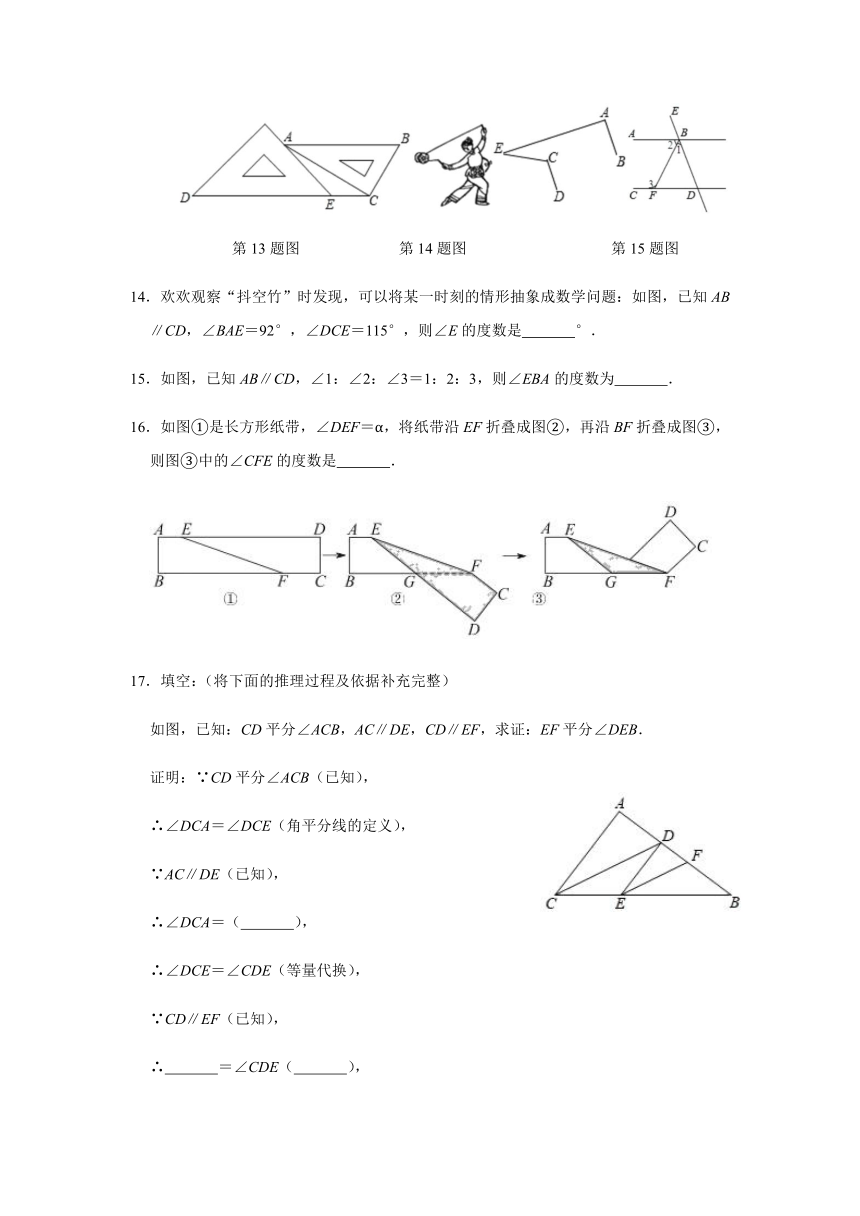
第10题图
第11题图
第12题图
11.如图,将长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′处,若∠AFE=68°,则∠C′EF等于( )
A.68°
B.80°
C.40°
D.55°
12.如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点作GP∥AB.则下列结论:
①∠AMF与∠DNF是同旁内角;②∠PGM=∠DNF;
③∠BMN+∠GHN=90°;④∠AMG+∠CHG=270°.
其中正确结论的个数是( )
A.1个
B.2
个
C.3个
D.4个
13.一副三角板按如图所示放置,AB∥DC,则∠CAE的度数为
.
第13题图
第14题图
第15题图
14.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是
°.
15.如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,则∠EBA的度数为
.
16.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是
.
17.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=(
),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴
=∠CDE(
),
∠DCE=∠BEF(
),
∴
=
(等量代换),
∴EF平分∠DEB(
).
18.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=72°,求∠2的度数.
19.如图1,AB∥CD,∠PAB=125°,∠PCD=115°,求∠APC的度数.
小明的思路是:过P作PM∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为
度;
(2)如图2,AB∥CD,点P在直线a上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点B、D两点不重合),请直接写出∠APC与α、β之间的数量关系
参考答案
1.B.2.B.3.45°.4.B.5.B.6.B.7.A.8.B.9.C.10.B.
11.A.12.C.13.15°.14.23.15.72°.16.180°﹣3α.
17.证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=∠CDE(两直线平行,内错角相等),
∴∠DCE=∠CDE(
等量代换),
∵CD∥EF
(
已知
),
∴∠DEF=∠CDE(两直线平行,内错角相等),
∠DCE=∠FEB(两直线平行,同位角相等),
∴∠DEF=∠FEB(等量代换),
∴EF平分∠DEB(
角平分线的定义
).
故答案为:∠CDE;∠DEF;两直线平行,内错角相等;两直线平行,同位角相等;∠DEF;∠FEB;角平分线的定义.
18.解:∵AB∥CD,
∴∠1+∠BEC=180°,
∵∠1=72°,
∴∠BEC=180°﹣72°=108°,
∵EG平分∠BEF,
∴∠BEG∠BEF108°=54°,
又∵AB∥CD,
∴∠BEG=∠2,
∴∠2的度数为54°.
19.解:(1)如图1,过P作PM∥AB,
∴∠APM+∠PAB=180°,
∴∠APM=180°﹣125°=55°,
∵AB∥CD,
∴PM∥CD,
∴∠CPM+∠PCD=180°,
∴∠CPM=180°﹣115°=65°,
∴∠APC=55°+65°=120°;
故答案为:120;
(2)如图2,∠APC=∠α+∠β,理由如下:
过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图3,当P在BD延长线时,∠APC=∠α﹣∠β;理由:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE﹣∠CPE=∠α﹣∠β;
如图4,当P在DB延长线时,∠APC=∠β﹣∠α;理由:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠CPE﹣∠APE=∠β﹣∠α;
第1课时
平行线的性质
1.如图,直线l与直线a、b相交,且a∥b,∠1=50°,则∠2的度数是( )
A.130°
B.50°
C.100°
D.120°
第1题图
第2题图
第3题图
2.如图,若AB∥CD,∠1=80°,则∠2的度数为( )
A.60°
B.80°
C.100°
D.120°
3.如图,AB∥CD,∠A=75°,∠C=30°,∠E的度数为
.
4.如图,已知AB∥CD,∠BED=90°,则∠1与∠2之间的数量关系可表示为( )
A.∠2=2∠1
B.∠2﹣∠1=90°
C.∠1+∠2=180°
D.无法表示
第4题图
第5题图
第6题图
5.如图,把一块含有60°角的直角三角尺的两个顶点放在直尺的对边上,∠1=20°,则∠2的度数是( )
A.30°
B.40°
C.45°
D.60°
6.若将一块三角板按如图所示的方式放置,AB∥CD,∠GEF=30°,∠1=52°,则∠2的度数为( )
A.20°
B.22°
C.27°
D.34°
7.如图,AB∥CD,∠2=150°,则∠1的度数是( )
A.30°
B.35°
C.40°
D.45°
第7题图
第8题图
第9题图
8.如图,已知AB∥CD,∠A=120°,∠C=130°,那么∠APC的度数是( )
A.100°
B.110°
C.120°
D.130°
9.如图,若l1∥l2,则∠1+∠2=180°的依据是( )
A.两直线平行,同位角相等
B.两直线平行,内错角相等
C.两直线平行,同旁内角互补
D.两直线平行,对顶角相等
10.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90°
B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180°
D.∠α+∠β+∠γ=180°
第10题图
第11题图
第12题图
11.如图,将长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′处,若∠AFE=68°,则∠C′EF等于( )
A.68°
B.80°
C.40°
D.55°
12.如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点作GP∥AB.则下列结论:
①∠AMF与∠DNF是同旁内角;②∠PGM=∠DNF;
③∠BMN+∠GHN=90°;④∠AMG+∠CHG=270°.
其中正确结论的个数是( )
A.1个
B.2
个
C.3个
D.4个
13.一副三角板按如图所示放置,AB∥DC,则∠CAE的度数为
.
第13题图
第14题图
第15题图
14.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是
°.
15.如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,则∠EBA的度数为
.
16.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是
.
17.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=(
),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴
=∠CDE(
),
∠DCE=∠BEF(
),
∴
=
(等量代换),
∴EF平分∠DEB(
).
18.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=72°,求∠2的度数.
19.如图1,AB∥CD,∠PAB=125°,∠PCD=115°,求∠APC的度数.
小明的思路是:过P作PM∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为
度;
(2)如图2,AB∥CD,点P在直线a上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点B、D两点不重合),请直接写出∠APC与α、β之间的数量关系
参考答案
1.B.2.B.3.45°.4.B.5.B.6.B.7.A.8.B.9.C.10.B.
11.A.12.C.13.15°.14.23.15.72°.16.180°﹣3α.
17.证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=∠CDE(两直线平行,内错角相等),
∴∠DCE=∠CDE(
等量代换),
∵CD∥EF
(
已知
),
∴∠DEF=∠CDE(两直线平行,内错角相等),
∠DCE=∠FEB(两直线平行,同位角相等),
∴∠DEF=∠FEB(等量代换),
∴EF平分∠DEB(
角平分线的定义
).
故答案为:∠CDE;∠DEF;两直线平行,内错角相等;两直线平行,同位角相等;∠DEF;∠FEB;角平分线的定义.
18.解:∵AB∥CD,
∴∠1+∠BEC=180°,
∵∠1=72°,
∴∠BEC=180°﹣72°=108°,
∵EG平分∠BEF,
∴∠BEG∠BEF108°=54°,
又∵AB∥CD,
∴∠BEG=∠2,
∴∠2的度数为54°.
19.解:(1)如图1,过P作PM∥AB,
∴∠APM+∠PAB=180°,
∴∠APM=180°﹣125°=55°,
∵AB∥CD,
∴PM∥CD,
∴∠CPM+∠PCD=180°,
∴∠CPM=180°﹣115°=65°,
∴∠APC=55°+65°=120°;
故答案为:120;
(2)如图2,∠APC=∠α+∠β,理由如下:
过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图3,当P在BD延长线时,∠APC=∠α﹣∠β;理由:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE﹣∠CPE=∠α﹣∠β;
如图4,当P在DB延长线时,∠APC=∠β﹣∠α;理由:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠CPE﹣∠APE=∠β﹣∠α;
