5.3 第2课时 平行线的性质和判定的综合运用-人教版七年级数学下册同步练习(Word版 含答案)
文档属性
| 名称 | 5.3 第2课时 平行线的性质和判定的综合运用-人教版七年级数学下册同步练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 140.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 21:30:17 | ||
图片预览



文档简介
5.3 平行线的性质
第2课时
平行线的性质和判定的综合运用
1.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b
B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c
D.∵∠2+∠3=180°,∴a∥c
2.如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80°
B.90°
C.100°
D.110°
3.下列说法正确的有( )
①平面内,不相交的两条直线是平行线;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平面内,过一点有且只有一条直线与已知直线平行;
④相等的角是对顶角;
⑤两角之和为180°,这两个角一定邻补角;
⑥P是直线a外一点,A、B、C分别是a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定是1.
A.1个
B.2个
C.3个
D.4个
4.下列说法中,错误的是( )
①a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系平行、相交、垂直三种.
A.3个
B.2个
C.1个
D.0个
5.将一副三角板的直角顶点重合按如图放置,小明得到下列结论:
①如果∠2=30°,则AC∥DE;
②∠BAE+∠CAD=180°;
③如果BC∥AD,则∠2=30°;
④如果∠CAD=150°,则∠4=∠C.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
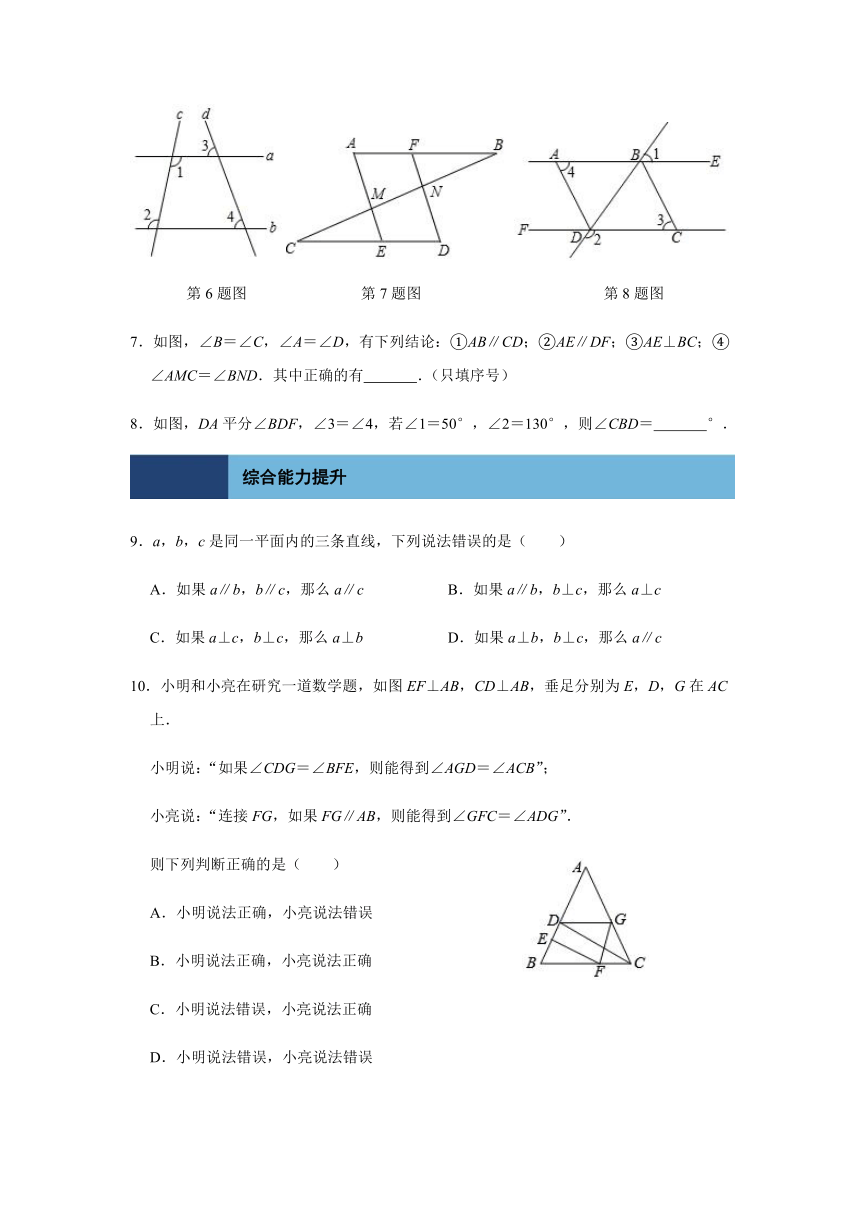
6.如图,直线a、b、c、d,若∠1=∠2,∠3=70°,则∠4=
.
第6题图
第7题图
第8题图
7.如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有
.(只填序号)
8.如图,DA平分∠BDF,∠3=∠4,若∠1=50°,∠2=130°,则∠CBD=
°.
9.a,b,c是同一平面内的三条直线,下列说法错误的是( )
A.如果a∥b,b∥c,那么a∥c
B.如果a∥b,b⊥c,那么a⊥c
C.如果a⊥c,b⊥c,那么a⊥b
D.如果a⊥b,b⊥c,那么a∥c
10.小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,垂足分别为E,D,G在AC上.
小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;
小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.
则下列判断正确的是( )
A.小明说法正确,小亮说法错误
B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确
D.小明说法错误,小亮说法错误
11.如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;
②AC∥BE;
③∠CBE+∠D=90°;
④∠DEB=2∠ABC,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
12.一条公路修到湖边时,需拐弯绕道而过,第一次拐弯∠A的度数为α,第二次拐弯∠B的度数为β,到了点C后需要继续拐弯,拐弯后与第一次拐弯之前的道路平行,则∠C的度数为( )
A.α﹣β
B.180°﹣β+α
C.360°﹣β﹣α
D.β﹣α
13.如图,∠AOB的一边OA为平面镜,∠AOB=38°45',在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是
.
14.如图,将一副三角板按如图所示放置,∠CAB=∠DAE=90°,∠C=45°,∠E=30°,则下列结论中:①∠1=∠3=45°;②若AD平分∠CAB,则有BC∥AE;③若AB平分∠DAE,则有BC∥AE;④若∠3=2∠2,则∠C=∠4;其中结论正确的选项有
.
第13题图
第14题图
15.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
16.如图,已知CD⊥AB,EF⊥AB,垂足分别为D,F,∠B+∠BDG=180°,试说明∠BEF=∠CDG.将下面的解答过程补充完整,并填空(填写理由依据或数学式,将答案按序号填在答题卷的对应位置内).
证明:∵CD⊥AB,EF⊥AB(
),
∴∠BFE=∠BDC=90°(
),
∴EF∥CD(
),
∴∠BEF=
(
),
又∵∠B+∠BDG=180°(
),
∴BC∥DG(
),
∴∠CDG=
(
),
∴∠CDG=∠BEF(
).
17.[感知]如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:
解;(1)如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.
[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,则∠G的度数是
°.
参考答案
1.D.2.C.3.B.4.B.5.C.6.70°.7.①②④.8.65.9.C.
10.A.11.D.12.B.13.77°30′.14.②③④.
15.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
16.证明:∵CD⊥AB,EF⊥AB(已知),
∴∠BFE=∠BDC=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠BEF=∠BCD(两直线平行,同位角相等),
又∵∠B+∠BDG=180°(已知),
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠CDG=∠BEF(等量代换).
故答案为:已知;垂直定义;同位角相等,两直线平行;∠BCD,两直线平行,同位角相等;已知,同旁内角互补,两直线平行;∠BCD,两直线平行,内错角相等;等量代换.
17.【解答】[探究]如图②,过点P作PM∥AB,
∴∠MPE=∠AEP=50°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠PFC=∠MPF=120°(两直线平行,内错角相等).
∴∠EPF=∠MPF﹣MPE=120°50°=70°(等式的性质).
答:∠EPF的度数为70°;
[应用]如图③所示,
∵EG是∠PEA的平分线,PG是∠PFC的平分线,
∴∠AEGAEP=25°,∠GCFPFC=60°,
过点G作GM∥AB,
∴∠MGE=∠AEG=25°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴GM∥CD(平行于同一条直线的两直线平行),
∴∠GFC=∠MGF=60°(两直线平行,内错角相等).
∴∠G=∠MGF﹣MGE=60°﹣25°=35°.
答:∠G的度数是35°.
故答案为:35.
第2课时
平行线的性质和判定的综合运用
1.如图,下列推理错误的是( )
A.∵∠1=∠2,∴a∥b
B.∵b∥c,∴∠2=∠4
C.∵a∥b,b∥c,∴a∥c
D.∵∠2+∠3=180°,∴a∥c
2.如图,在由四条直线相交形成的图形中,若∠1=70°,∠2=80°,∠3=110°,则∠4的大小为( )
A.80°
B.90°
C.100°
D.110°
3.下列说法正确的有( )
①平面内,不相交的两条直线是平行线;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平面内,过一点有且只有一条直线与已知直线平行;
④相等的角是对顶角;
⑤两角之和为180°,这两个角一定邻补角;
⑥P是直线a外一点,A、B、C分别是a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定是1.
A.1个
B.2个
C.3个
D.4个
4.下列说法中,错误的是( )
①a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系平行、相交、垂直三种.
A.3个
B.2个
C.1个
D.0个
5.将一副三角板的直角顶点重合按如图放置,小明得到下列结论:
①如果∠2=30°,则AC∥DE;
②∠BAE+∠CAD=180°;
③如果BC∥AD,则∠2=30°;
④如果∠CAD=150°,则∠4=∠C.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
6.如图,直线a、b、c、d,若∠1=∠2,∠3=70°,则∠4=
.
第6题图
第7题图
第8题图
7.如图,∠B=∠C,∠A=∠D,有下列结论:①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有
.(只填序号)
8.如图,DA平分∠BDF,∠3=∠4,若∠1=50°,∠2=130°,则∠CBD=
°.
9.a,b,c是同一平面内的三条直线,下列说法错误的是( )
A.如果a∥b,b∥c,那么a∥c
B.如果a∥b,b⊥c,那么a⊥c
C.如果a⊥c,b⊥c,那么a⊥b
D.如果a⊥b,b⊥c,那么a∥c
10.小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,垂足分别为E,D,G在AC上.
小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;
小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.
则下列判断正确的是( )
A.小明说法正确,小亮说法错误
B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确
D.小明说法错误,小亮说法错误
11.如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;
②AC∥BE;
③∠CBE+∠D=90°;
④∠DEB=2∠ABC,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
12.一条公路修到湖边时,需拐弯绕道而过,第一次拐弯∠A的度数为α,第二次拐弯∠B的度数为β,到了点C后需要继续拐弯,拐弯后与第一次拐弯之前的道路平行,则∠C的度数为( )
A.α﹣β
B.180°﹣β+α
C.360°﹣β﹣α
D.β﹣α
13.如图,∠AOB的一边OA为平面镜,∠AOB=38°45',在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB的度数是
.
14.如图,将一副三角板按如图所示放置,∠CAB=∠DAE=90°,∠C=45°,∠E=30°,则下列结论中:①∠1=∠3=45°;②若AD平分∠CAB,则有BC∥AE;③若AB平分∠DAE,则有BC∥AE;④若∠3=2∠2,则∠C=∠4;其中结论正确的选项有
.
第13题图
第14题图
15.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
16.如图,已知CD⊥AB,EF⊥AB,垂足分别为D,F,∠B+∠BDG=180°,试说明∠BEF=∠CDG.将下面的解答过程补充完整,并填空(填写理由依据或数学式,将答案按序号填在答题卷的对应位置内).
证明:∵CD⊥AB,EF⊥AB(
),
∴∠BFE=∠BDC=90°(
),
∴EF∥CD(
),
∴∠BEF=
(
),
又∵∠B+∠BDG=180°(
),
∴BC∥DG(
),
∴∠CDG=
(
),
∴∠CDG=∠BEF(
).
17.[感知]如图①,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:
解;(1)如图①,过点P作PM∥AB,
∴∠1=∠AEP=40°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠2+∠PFD=180°(两直线平行,同旁内角互补).
∵∠PFD=130°(已知),
∴∠2=180°﹣130°=50°(等式的性质),
∴∠1+∠2=40°+50°=90°(等式的性质).
即∠EPF=90°(等量代换).
[探究]如图②,AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.
[应用]如图③所示,在[探究]的条件下,∠PEA的平分线和∠PFC的平分线交于点G,则∠G的度数是
°.
参考答案
1.D.2.C.3.B.4.B.5.C.6.70°.7.①②④.8.65.9.C.
10.A.11.D.12.B.13.77°30′.14.②③④.
15.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
16.证明:∵CD⊥AB,EF⊥AB(已知),
∴∠BFE=∠BDC=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠BEF=∠BCD(两直线平行,同位角相等),
又∵∠B+∠BDG=180°(已知),
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠CDG=∠BEF(等量代换).
故答案为:已知;垂直定义;同位角相等,两直线平行;∠BCD,两直线平行,同位角相等;已知,同旁内角互补,两直线平行;∠BCD,两直线平行,内错角相等;等量代换.
17.【解答】[探究]如图②,过点P作PM∥AB,
∴∠MPE=∠AEP=50°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴PM∥CD(平行于同一条直线的两直线平行),
∴∠PFC=∠MPF=120°(两直线平行,内错角相等).
∴∠EPF=∠MPF﹣MPE=120°50°=70°(等式的性质).
答:∠EPF的度数为70°;
[应用]如图③所示,
∵EG是∠PEA的平分线,PG是∠PFC的平分线,
∴∠AEGAEP=25°,∠GCFPFC=60°,
过点G作GM∥AB,
∴∠MGE=∠AEG=25°(两直线平行,内错角相等)
∵AB∥CD(已知),
∴GM∥CD(平行于同一条直线的两直线平行),
∴∠GFC=∠MGF=60°(两直线平行,内错角相等).
∴∠G=∠MGF﹣MGE=60°﹣25°=35°.
答:∠G的度数是35°.
故答案为:35.
