5.1 第3课时 同位角、内错角、同旁内角-人教版七年级数学下册同步练习(Word版 含答案)
文档属性
| 名称 | 5.1 第3课时 同位角、内错角、同旁内角-人教版七年级数学下册同步练习(Word版 含答案) | 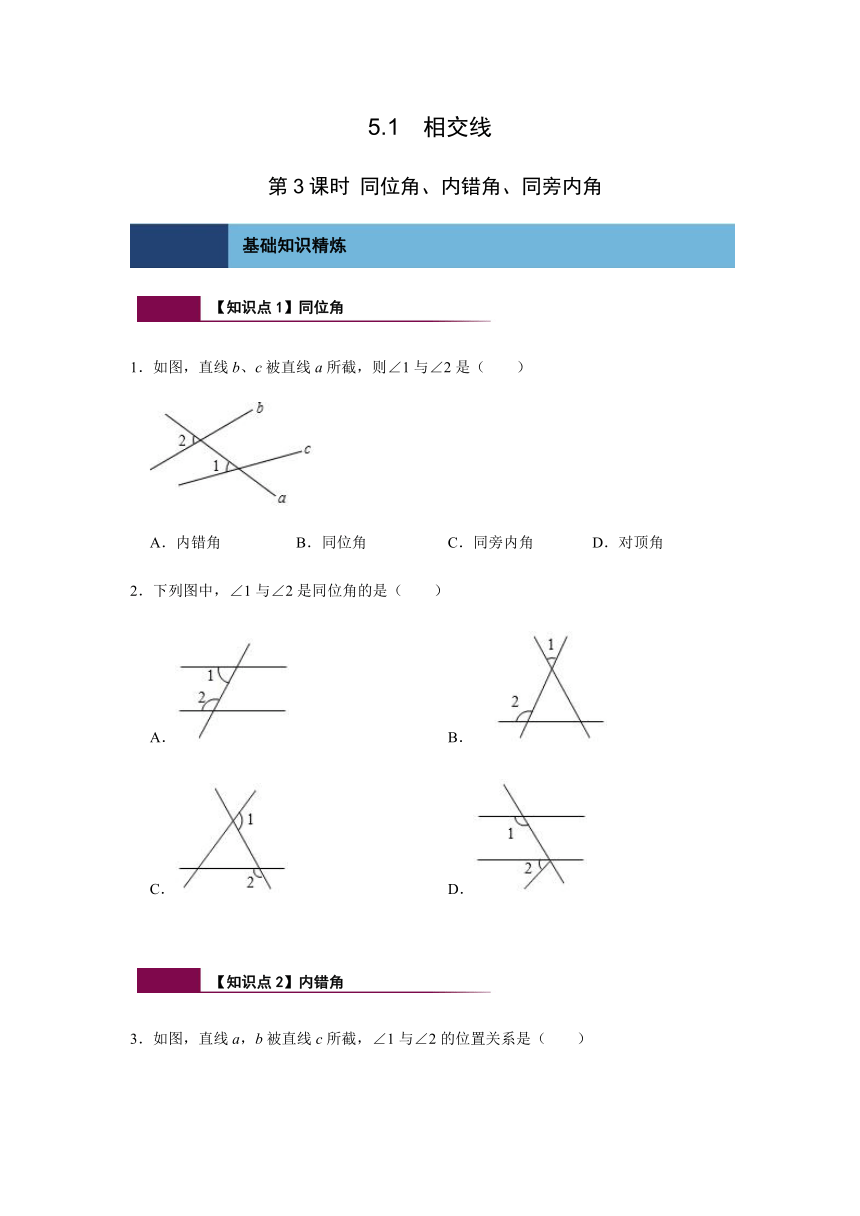 | |
| 格式 | docx | ||
| 文件大小 | 113.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 21:32:38 | ||
图片预览


文档简介
5.1 相交线
第3课时
同位角、内错角、同旁内角
1.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角
B.同位角
C.同旁内角
D.对顶角
2.下列图中,∠1与∠2是同位角的是( )
A.
B.
C.
D.
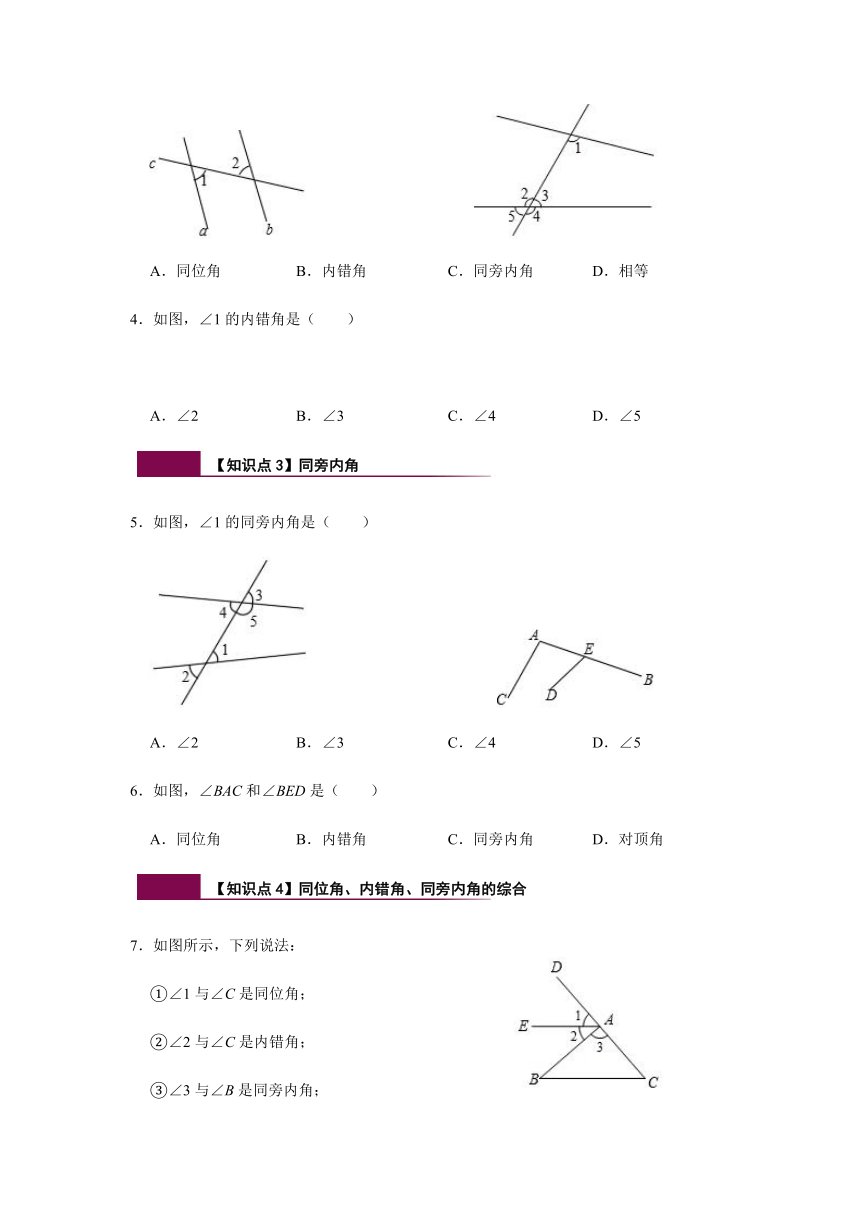
3.如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
A.同位角
B.内错角
C.同旁内角
D.相等
4.如图,∠1的内错角是( )
A.∠2
B.∠3
C.∠4
D.∠5
5.如图,∠1的同旁内角是( )
A.∠2
B.∠3
C.∠4
D.∠5
6.如图,∠BAC和∠BED是( )
A.同位角
B.内错角
C.同旁内角
D.对顶角
7.如图所示,下列说法:
①∠1与∠C是同位角;
②∠2与∠C是内错角;
③∠3与∠B是同旁内角;
④∠3与∠C是同旁内角.
其中正确的是( )
A.①②③
B.②③④
C.①③④
D.①②④
8.如图所示,下列说法中,错误的是( )
A.∠A与∠EDC是同位角
B.∠A与∠C是同旁内角
C.∠A与∠ADC是同旁内角
D.∠A与∠ABF是内错角
9.如图,按角的位置关系填空:∠1与∠2是
角,∠1与∠3是
角,∠2与∠3是
角.
10.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角
B.∠1与∠4是内错角
C.∠5与∠6是内错角
D.∠3与∠5是同位角
11.如图,在△ABC中,以点C为顶点,在△ABC外画∠ACD=∠A,且点A与D在直线BC的同一侧,再延长BC至点E,在作的图形中,∠A与
是内错角;∠B与
是同位角;∠ACB与
是同旁内角.
12.如图,直线AB,CD与直线EF相交,∠5和
是同位角,和
是内错角,和
是同旁内角.∠2和
是直线
、
被
所截而形成的同位角.
13.如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
14.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
15.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了
对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有
对同旁内角.
(3)平面内四条直线两两相交,最多可以形成
对同旁内角.
(4)平面内n条直线两两相交,最多可以形成
对同旁内角.
16.已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.
路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.
试一试:(1)从起始∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?
参考答案
1.B.2.B.3.B.4.A.5.D.6.A.7.C.8.B.9.同旁内,内错,邻补.10.B.
11.∠ACD、∠ACE;∠DCE、∠ACE;∠A、∠B.
12.∠1,∠3,∠2,∠6,AB,CD,EF.
13.解:由图可得:
同位角:∠1与∠3,∠3与∠5;
内错角:∠1与∠4,∠4与∠5;
同旁内角:∠1与∠2,∠6与∠5.
14.解:(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°,∠2=72°,∠1=144°.
15.解:因为两个交点可以形成2对同旁内角,而三个交点形成的同旁内角的对数为6对,
(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有3×2=6对同旁内角.
(3)平面内四条直线两两相交,交点最多为6个,最多可以形成4×(4﹣1)×(4﹣2)=24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
16.【解答】解:(1)路径∠1∠12∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点∠8.其路径为:
路径:∠1∠10∠5∠8.
第3课时
同位角、内错角、同旁内角
1.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角
B.同位角
C.同旁内角
D.对顶角
2.下列图中,∠1与∠2是同位角的是( )
A.
B.
C.
D.
3.如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
A.同位角
B.内错角
C.同旁内角
D.相等
4.如图,∠1的内错角是( )
A.∠2
B.∠3
C.∠4
D.∠5
5.如图,∠1的同旁内角是( )
A.∠2
B.∠3
C.∠4
D.∠5
6.如图,∠BAC和∠BED是( )
A.同位角
B.内错角
C.同旁内角
D.对顶角
7.如图所示,下列说法:
①∠1与∠C是同位角;
②∠2与∠C是内错角;
③∠3与∠B是同旁内角;
④∠3与∠C是同旁内角.
其中正确的是( )
A.①②③
B.②③④
C.①③④
D.①②④
8.如图所示,下列说法中,错误的是( )
A.∠A与∠EDC是同位角
B.∠A与∠C是同旁内角
C.∠A与∠ADC是同旁内角
D.∠A与∠ABF是内错角
9.如图,按角的位置关系填空:∠1与∠2是
角,∠1与∠3是
角,∠2与∠3是
角.
10.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角
B.∠1与∠4是内错角
C.∠5与∠6是内错角
D.∠3与∠5是同位角
11.如图,在△ABC中,以点C为顶点,在△ABC外画∠ACD=∠A,且点A与D在直线BC的同一侧,再延长BC至点E,在作的图形中,∠A与
是内错角;∠B与
是同位角;∠ACB与
是同旁内角.
12.如图,直线AB,CD与直线EF相交,∠5和
是同位角,和
是内错角,和
是同旁内角.∠2和
是直线
、
被
所截而形成的同位角.
13.如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
14.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
15.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了
对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有
对同旁内角.
(3)平面内四条直线两两相交,最多可以形成
对同旁内角.
(4)平面内n条直线两两相交,最多可以形成
对同旁内角.
16.已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.
路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.
试一试:(1)从起始∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?
参考答案
1.B.2.B.3.B.4.A.5.D.6.A.7.C.8.B.9.同旁内,内错,邻补.10.B.
11.∠ACD、∠ACE;∠DCE、∠ACE;∠A、∠B.
12.∠1,∠3,∠2,∠6,AB,CD,EF.
13.解:由图可得:
同位角:∠1与∠3,∠3与∠5;
内错角:∠1与∠4,∠4与∠5;
同旁内角:∠1与∠2,∠6与∠5.
14.解:(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°,∠2=72°,∠1=144°.
15.解:因为两个交点可以形成2对同旁内角,而三个交点形成的同旁内角的对数为6对,
(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有3×2=6对同旁内角.
(3)平面内四条直线两两相交,交点最多为6个,最多可以形成4×(4﹣1)×(4﹣2)=24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
16.【解答】解:(1)路径∠1∠12∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点∠8.其路径为:
路径:∠1∠10∠5∠8.
