人教版七年级数学下册5.2.2 平行线的判定 课时练习(Word版 含答案)
文档属性
| 名称 | 人教版七年级数学下册5.2.2 平行线的判定 课时练习(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 339.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 23:52:03 | ||
图片预览



文档简介
5.2.2
平行线的判定
课时练习
一、单选题
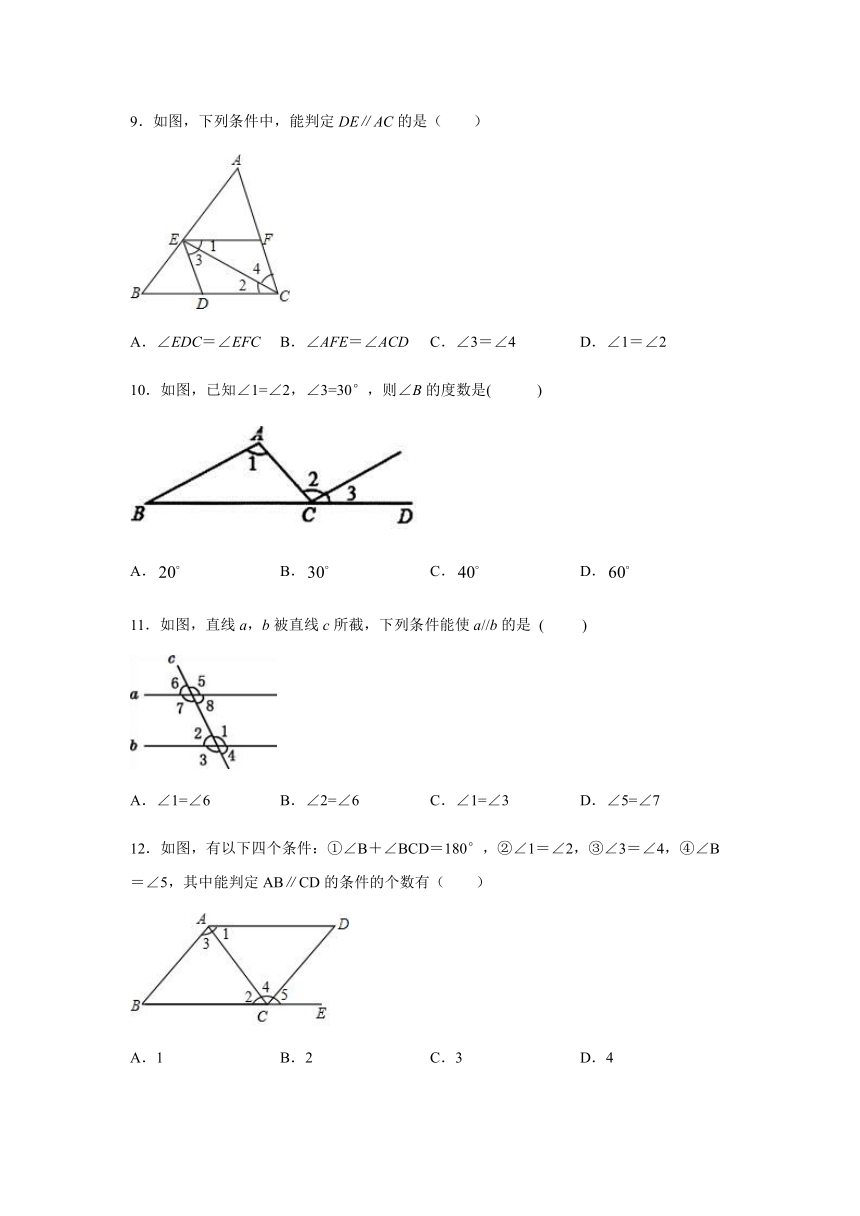
1.如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是(
)
A.∠1=∠3
B.∠2+∠4=180°
C.∠1=∠4
D.∠1+∠4=180°
2.如图,下列条件:中能判断直线的有(
)
A.5个
B.4个
C.3个
D.2个
3.如图,下列说法错误的是(
)
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
4.如图,直线被直线所截,,下列条件中能判定的是(
)
A.
B.
C.
D.
5.已知如图直线a,b被直线c所截,下列条件能判断a∥b的是(
)
A.∠1=∠2
B.∠2=∠3
C.∠1=∠4
D.∠2+∠5=180°
6.如图,在下列条件中,能判断AD∥BC的是(
)
A.∠DAC=∠BCA
B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC
D.∠BAC=∠ACD
7.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.
B.
C.
D.
8.如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是(
)
A.∠1=∠2
B.∠3=∠4
C.∠2=∠4
D.∠1=∠4
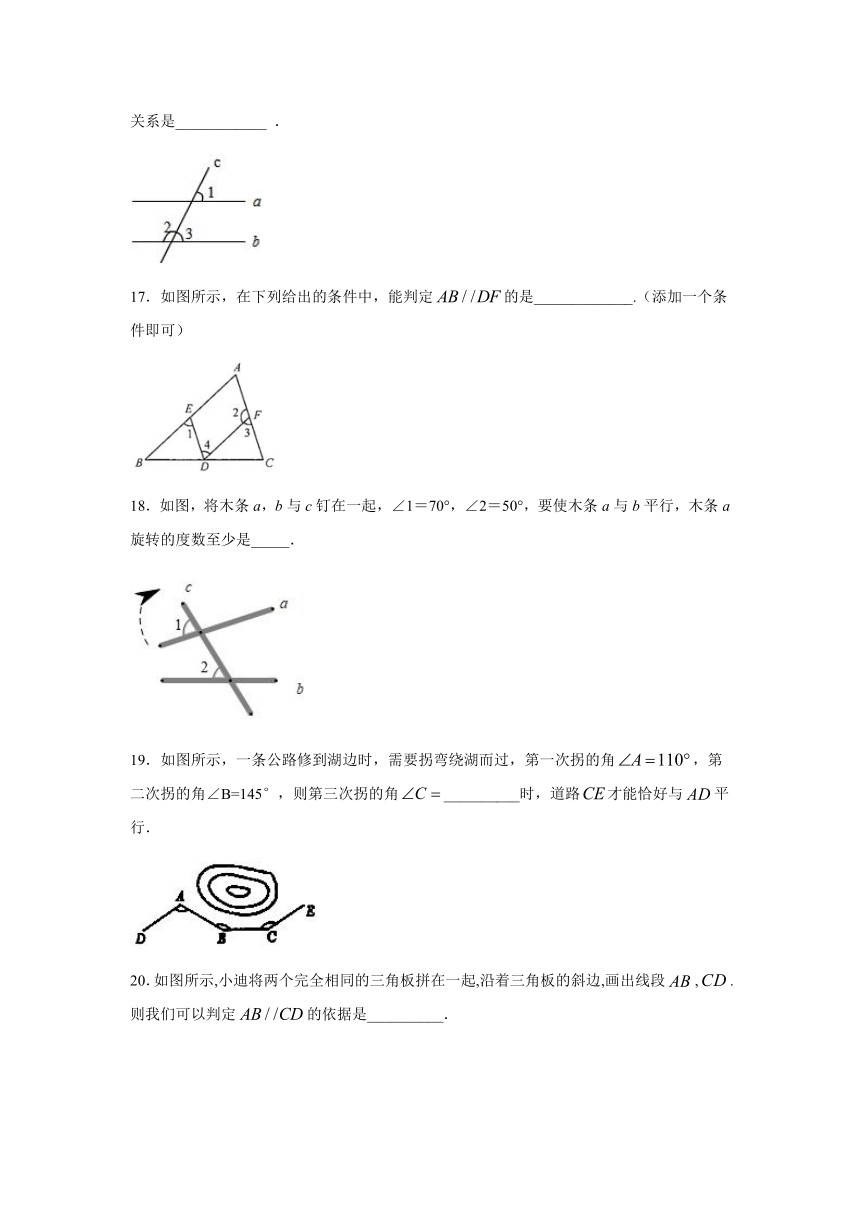
9.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC
B.∠AFE=∠ACD
C.∠3=∠4
D.∠1=∠2
10.如图,已知∠1=∠2,∠3=30°,则∠B的度数是(
)
A.
B.
C.
D.
11.如图,直线a,b被直线c所截,下列条件能使a//b的是
(
)
A.∠1=∠6
B.∠2=∠6
C.∠1=∠3
D.∠5=∠7
12.如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,其中能判定AB∥CD的条件的个数有(
)
A.1
B.2
C.3
D.4
13.如图,下列条件中能判定AB∥CD的是(
)
A.∠B=∠D;
B.∠DAB+∠D=180°;
C.∠1=∠2;
D.∠D+∠BCD=180°.
14.如图下列推断错误的是(
)
A.由,得
B.由,得
C.由,得
D.由,得
15.如图,不能判定AB∥CD的是(
)
A.∠B=∠DCE
B.∠A=∠ACD
C.∠B+∠BCD=180°
D.∠A=∠DCE
二、填空题
16.如图,两直线a.b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a.b的位置关系是____________
.
17.如图所示,在下列给出的条件中,能判定的是_____________.(添加一个条件即可)
18.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是_____.
19.如图所示,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角,第二次拐的角∠B=145°,则第三次拐的角__________时,道路才能恰好与平行.
20.如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段,.则我们可以判定的依据是__________.
三、解答题
21.填空,完成下列说理过程.
如图所示,直线AB.CD被直线CE所截,点A在CE上,AF平分交CD于点F,且,那么AB与CD平行吗?请说明理由.
解:∵AF平分,
∴________(_______________).
∵,∴__________(等量代换).
∴(________________).
22.如图,已知∠1=∠2,∠2=∠3,请写出图中所有互相平行的线,并证明.
23.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)
CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
24.填空,如图所示.
(1)∵
(已知),∴__________________
(
).
(2)∵
(已知),∴__________________(
).
(3)∵_________(已知),∴(
).
25.在中,D是BC边上一点,且,MN是经过点D的一条直线.
(1)若直线,垂足为点E.
①依题意补全图1.
②若,则________,________.
如图2,若直线MN交AC边于点F,且,求证:
参考答案
1--10DBCCA
ABDCB
11--15BCBCD
16.平行
17.(答案不唯一)
18.20°
19.145°
20.内错角相等,两直线平行
21.∵AF平分,
∴2(角平分线定义).
∵,
∴3(等量代换).
∴(内错角相等,两直线平行).
故答案为:2;角平分线定义;3;内错角相等,两直线平行.
22.因为∠1=∠2(已知)
所以a∥d(同位角相等,两直线平行)
因为∠2=∠3(已知)
所以b∥d(同位角相等,两直线平行)
所以a∥b∥d(平行线的传递性).
23.(1)CD与EF平行.理由如下:
CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°
∴EF∥CD
(2)
如图:
EF∥CD,
∴∠2=∠BCD
又∠1=∠2,
∴∠1=∠BCD
∴DG∥BC,
∴∠ACB=∠3=115°.
24.(1)∵
(已知),
∴CDAB(内错角相等,两直线平行)
故答案为:CD;AB;内错角相等,两直线平行;
(2)∵
(已知),
∴BDAC(同位角相等,两直线平行)
故答案为:BD;AC;同位角相等,两直线平行;
(3)∵(已知),
∴(同旁内角互补,两直线平行).
故答案为:;同旁内角互补,两直线平行.
25.(1)①如图所示.
②,
.
,
.
,
.
故答案为.
(2),
且,
.
.
平行线的判定
课时练习
一、单选题
1.如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是(
)
A.∠1=∠3
B.∠2+∠4=180°
C.∠1=∠4
D.∠1+∠4=180°
2.如图,下列条件:中能判断直线的有(
)
A.5个
B.4个
C.3个
D.2个
3.如图,下列说法错误的是(
)
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
4.如图,直线被直线所截,,下列条件中能判定的是(
)
A.
B.
C.
D.
5.已知如图直线a,b被直线c所截,下列条件能判断a∥b的是(
)
A.∠1=∠2
B.∠2=∠3
C.∠1=∠4
D.∠2+∠5=180°
6.如图,在下列条件中,能判断AD∥BC的是(
)
A.∠DAC=∠BCA
B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC
D.∠BAC=∠ACD
7.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.
B.
C.
D.
8.如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是(
)
A.∠1=∠2
B.∠3=∠4
C.∠2=∠4
D.∠1=∠4
9.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC
B.∠AFE=∠ACD
C.∠3=∠4
D.∠1=∠2
10.如图,已知∠1=∠2,∠3=30°,则∠B的度数是(
)
A.
B.
C.
D.
11.如图,直线a,b被直线c所截,下列条件能使a//b的是
(
)
A.∠1=∠6
B.∠2=∠6
C.∠1=∠3
D.∠5=∠7
12.如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,其中能判定AB∥CD的条件的个数有(
)
A.1
B.2
C.3
D.4
13.如图,下列条件中能判定AB∥CD的是(
)
A.∠B=∠D;
B.∠DAB+∠D=180°;
C.∠1=∠2;
D.∠D+∠BCD=180°.
14.如图下列推断错误的是(
)
A.由,得
B.由,得
C.由,得
D.由,得
15.如图,不能判定AB∥CD的是(
)
A.∠B=∠DCE
B.∠A=∠ACD
C.∠B+∠BCD=180°
D.∠A=∠DCE
二、填空题
16.如图,两直线a.b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a.b的位置关系是____________
.
17.如图所示,在下列给出的条件中,能判定的是_____________.(添加一个条件即可)
18.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是_____.
19.如图所示,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角,第二次拐的角∠B=145°,则第三次拐的角__________时,道路才能恰好与平行.
20.如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段,.则我们可以判定的依据是__________.
三、解答题
21.填空,完成下列说理过程.
如图所示,直线AB.CD被直线CE所截,点A在CE上,AF平分交CD于点F,且,那么AB与CD平行吗?请说明理由.
解:∵AF平分,
∴________(_______________).
∵,∴__________(等量代换).
∴(________________).
22.如图,已知∠1=∠2,∠2=∠3,请写出图中所有互相平行的线,并证明.
23.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)
CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
24.填空,如图所示.
(1)∵
(已知),∴__________________
(
).
(2)∵
(已知),∴__________________(
).
(3)∵_________(已知),∴(
).
25.在中,D是BC边上一点,且,MN是经过点D的一条直线.
(1)若直线,垂足为点E.
①依题意补全图1.
②若,则________,________.
如图2,若直线MN交AC边于点F,且,求证:
参考答案
1--10DBCCA
ABDCB
11--15BCBCD
16.平行
17.(答案不唯一)
18.20°
19.145°
20.内错角相等,两直线平行
21.∵AF平分,
∴2(角平分线定义).
∵,
∴3(等量代换).
∴(内错角相等,两直线平行).
故答案为:2;角平分线定义;3;内错角相等,两直线平行.
22.因为∠1=∠2(已知)
所以a∥d(同位角相等,两直线平行)
因为∠2=∠3(已知)
所以b∥d(同位角相等,两直线平行)
所以a∥b∥d(平行线的传递性).
23.(1)CD与EF平行.理由如下:
CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°
∴EF∥CD
(2)
如图:
EF∥CD,
∴∠2=∠BCD
又∠1=∠2,
∴∠1=∠BCD
∴DG∥BC,
∴∠ACB=∠3=115°.
24.(1)∵
(已知),
∴CDAB(内错角相等,两直线平行)
故答案为:CD;AB;内错角相等,两直线平行;
(2)∵
(已知),
∴BDAC(同位角相等,两直线平行)
故答案为:BD;AC;同位角相等,两直线平行;
(3)∵(已知),
∴(同旁内角互补,两直线平行).
故答案为:;同旁内角互补,两直线平行.
25.(1)①如图所示.
②,
.
,
.
,
.
故答案为.
(2),
且,
.
.
