北师大版七年级数学下册 第三章 变量之间的关系 单元检测试题(Word版 含答案)
文档属性
| 名称 | 北师大版七年级数学下册 第三章 变量之间的关系 单元检测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 35.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-01 23:59:21 | ||
图片预览




文档简介
1203960011391900第三章 变量之间的关系 单元检测试题
班级:_____________姓名:_____________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 人的身高h随时间t的变化而变化,那么下列说法正确的是( )
A.h,t都是不变量 B.t是自变量,h是因变量
C.h,t都是自变量 D.h是自变量,t是因变量?
2. 半径是R的圆的周长C=2πR,下列说法正确的是(? ? ? ? )
A.C,π,R是变量
B.C是变量,2,π,R是常量
C.R是变量,2,π,C是常量
D.C,R是变量,2,π是常量?
3. 在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器的容积?
4. 当圆的半径发生变化时,面积也发生变化,圆面积S与半径r的关系为S=πr2.下面的说法中,正确的是( )
A.S,π,r都是变量 B.只有r是变量
C.S,r是变量,π是常量 D.S,π,r都是常量?
5. 汽车在匀速行驶过程中,路程s、速度v、时间t之间的关系为s=vt,下列说法正确的是(? ? ? ? )
A.s、v、t都是变量?? B.s、t是变量,v是常量
C.v、t是变量,s是常量?? D.s、v是变量,t是常量
?
6. 甲、乙两地相距50千米,若一辆汽车以50千米/时的速度从甲地到乙地,则汽车距乙地的路程s(千米)与行驶的时间t(时)之间的关系式s=50-50t(0≤t≤1)中,常量的个数为( )
A.1个 B.2个 C.3个 D.4个?
7. 如果用总长为60m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为p(m),一边长为a(m),那么S,p,a中是变量的是(? ? ? ? )
A.S和p B.S和a C.p和a D.S,p,a?
8. 以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t-4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t,h是变量
B.v0是常量,t,h是变量
C.v0,-4.9是常量,t,h是变量
D.4.9是常量,v0,t,h是变量?
9. 已知圆柱体的高是10厘米,沿着底面直径垂直切开,把圆柱分成相等的两半,表面积增加了40平方厘米,这个圆柱体的体积是( )立方厘米。(全卷π均取3.14)
A.62.8 B.125.6 C.31.4 D.251.2?
10. 弹簧挂上物体会伸长,测得一弹簧的长度x(cm)与所挂的物体的重量y(kg)间的关系如下表:
x
0
1
2
3
4
5
6
y
10
10.5
11
11.5
12
12.5
13
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂物体时的长度为0cm
C.物体质量每增加1kg,弹簧的长度y增加0.5cm
D.所挂的物体的质量为7kg时,弹簧的长度为13.5cm
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. “日落西山”是我们每天都要面对的自然变换,就你的理解,________是自变量,________是因变量. ?
12. 圆的半径为r,圆的面积S与半径r之间有如下关系:S=πr2.在这关系中,常量是________.
13. 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就是说x是________,y是x的________.
14. 一圆锥的底面半径是5cm,当圆锥的高由2cm变到10cm时,圆锥的体积由________cm3变到________cm3.
15. 2B铅笔每枝0.5元,买n枝需W元,其中常量是________,变量是________. ?
16. 每个同学购买一本课本,课本的单价是4.5元,总金额为y(元),学生数为n(个),则变量是________,常量是________. ?
17. 某公司销售部门发现,该公司的销售收入随销售量的变化而变化,在这个变化过程中,自变量是________. ?
18. 在公式s=v0t+2t2(v0为已知数)中,常量是________,变量是________. ?
19. 大家知道,冰层越厚,所承受的压力越大,这其中自变量是________,因变量是________. ?
20. 某公司2020年年终财务报表显示,该公司2020年年终每股净利润为m元.年报公布后的某日,该公司的股票收盘价为x元,所以这天收盘后该股票的市盈率为y=xm,在这三个字母中其中常量是________,变量是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , )
21. 齿轮每分钟120转,如果n表示转数,t表示转动时间.
(1)用n的代数式表示t;
(2)说出其中的变量与常量.
?
22. 设路程为s?km,速度为v?km/h,时间t?h,指出下列各式中的常量与变量.
(1)v=s8;
(2)s=4.5t-2t2;
(3)vt=100.
?
23. 下表是某公共电话亭打长途电话的几次收费记录:
时间(分)
1
2
3
4
5
6
7
电话费(元)
0.6
1.2
1.8
2.4
3.0
3.6
4.2
(1)上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示时间,y表示电话费,那么随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
?
24. 阅读下面这段有关“龟兔赛跑”的寓言故事,并指出所涉及的量中,哪些是常量,哪些是变量.
一次乌龟与兔子举行500米赛跑,比赛开始不久,兔子就遥遥领先.当兔子以20米/分的速度跑了10分时,往回一看,乌龟远远地落在后面呢!兔子心想:“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢?”可是,当骄傲的兔子正做着胜利者的美梦时,勤勉的乌龟却从它身边悄悄爬过,并以10米/分的速度匀速爬向终点.40分后,兔子梦醒了,而此时乌龟刚好到达终点.兔子悔之晚矣,等它再以30米/分的速度跑向终点时,它比乌龟足足晚了10分.
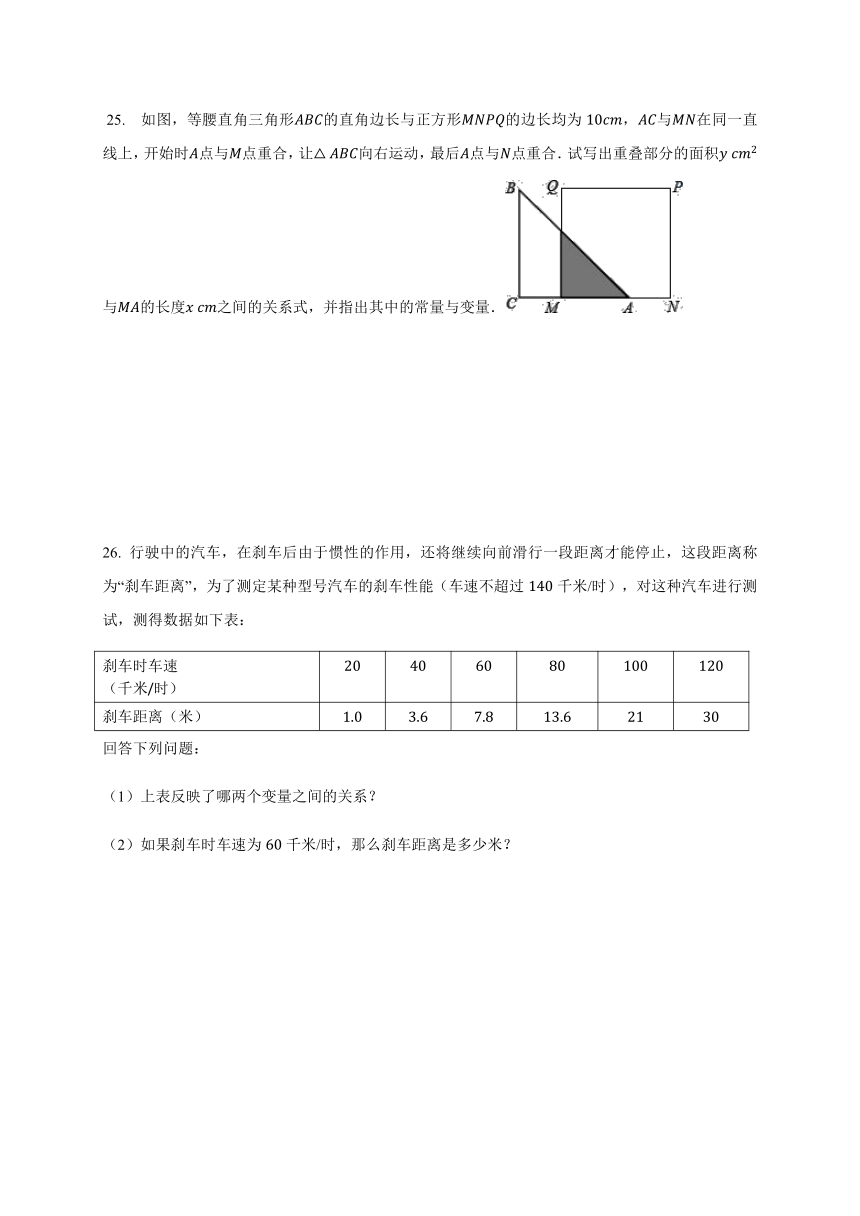
?25. 如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积y?cm2与MA的长度x?cm之间的关系式,并指出其中的常量与变量.
?
26. 行驶中的汽车,在刹车后由于惯性的作用,还将继续向前滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能(车速不超过140千米/时),对这种汽车进行测试,测得数据如下表:
刹车时车速
(千米/时)
20
40
60
80
100
120
刹车距离(米)
1.0
3.6
7.8
13.6
21
30
回答下列问题:
(1)上表反映了哪两个变量之间的关系?
(2)如果刹车时车速为60千米/时,那么刹车距离是多少米?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:因为人的身高h随时间t的变化而变化,所以t是自变量,h是因变量;
故本题选B.
2.
【答案】
D
【解答】
解:在某一个变化过程中可以取不同数值的量叫变量,
数值始终不变的量叫常量.
故由常量与变量的定义可得,
在半径是R的圆的周长C=2πR中,
C,R是变量,2,π是常量.
故选D.
3.
【答案】
B
【解答】
解:根据函数的定义可知,水温是随着所晒时间的长短而变化,可知水温是因变量,太阳照晒时间的长短为自变量.
故选B.
4.
【答案】
C
【解答】
解:圆的半径发生变化时,面积也发生变化,圆面积S与半径r的关系为S=πr2,S、r是变量,π是常量,
故选:C.
5.
【答案】
B
【解答】
解:汽车在匀速行驶过程中,速度v不变,是常量,t、s是变量.
故选B.
6.
【答案】
B
【解答】
解:汽车距乙地的路程s(千米)与行驶的时间t(时)之间的关系式s=50-50t(0≤t≤1)中,常量为距离50千米和速度50千米/时两个,
故选B.
7.
【答案】
B
【解答】
解:∵ 篱笆的总长为60米,
∴ 周长p是定值,而面积S和一边长a是变量,
故选B.
8.
【答案】
C
【解答】
解:h=v0t-4.9t2中的v0(米/秒)是固定的速度,-4.9是定值,
故v0和-4.9是常量,t,h是变量,
故选C.
9.
【答案】
C
【解答】
解:设底面圆的半径是r厘米,
根据题意得:10×2×2r=40
解得I=1
∴ 圆柱体积=π×12×10×31.4立方厘米.
故答案为:C.
10.
【答案】
B
【解答】
解:A,y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B,弹簧不挂重物时的长度为10cm,故B选项错误;
C,物体质量每增加1kg,弹簧长度y增加0.5cm,故C选项正确;
D,由C知,y=10+0.5x,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确.
故选B.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
时间,日落
【解答】
解:“日落西山”是我们每天都要面对的自然变换,就你的理解,时间是自变量,日落是因变量.
故答案是:时间,日落.
12.
【答案】
π
【解答】
解:在S=πr2中π是一个常数(圆周率),即π是常量,S,r是两个变量.
故填π.
13.
【答案】
自变量,函数
【解答】
解:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就是说x是自变量,y是x的函数.
故答案为:自变量,函数.
14.
【答案】
50π3,250π3
【解答】
解圆锥的底面半径是5cm,当圆锥的高由2cm变到10cm时,圆锥的体积由?50π3cm3变到?250π3cm3:,
故答案为:50π3,250π3.
15.
【答案】
0.5,n,W
【解答】
解:铅笔的单价固定,总钱数随着铅笔支数的变化而变化,故常量是0.5,变量是n,W,
故答案为:0.5;n,W.
16.
【答案】
y,n,4.5
【解答】
解:∵ 单价固定,
∴ 常量是4.5,
∵ 总金额为y(元)随着学生数为n(个)的变化而变化,
∴ y,n是变量,
故答案为y,n;4.5.
17.
【答案】
销售量
【解答】
解:该公司的销售收入随销售量的变化而变化,在这个变化过程中,自变量是销售量.
故答案为:销售量.
18.
【答案】
v0,2,s,t
【解答】
解:因为在公式s=v0t+2t2(v0为已知数),所以v0、2是常量,s、t是变量.
19.
【答案】
冰层的厚度,冰层所承受的压力
【解答】
解:大家知道,冰层越厚,所承受的压力越大,这其中自变量是冰层的厚度,因变量是冰层所承受的压力;
故答案为:冰层的厚度,冰层所承受的压力.
20.
【答案】
m,x,y
【解答】
解:y=xm中的三个字母中其中常量是m,变量是x,y,
故答案为:m;x,y.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:(1)由题意得:
120t=n,
t=n120;
(2)变量:t,n常量:120.
【解答】
解:(1)由题意得:
120t=n,
t=n120;
(2)变量:t,n常量:120.
22.
【答案】
解:(1)常量是8,变量是v,s;
(2)常量是4.5,2,变量是s,t;
(3)常量是100,变量是v,t.
【解答】
解:(1)常量是8,变量是v,s;
(2)常量是4.5,2,变量是s,t;
(3)常量是100,变量是v,t.
23.
【答案】
解:(1)上表反应的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)根据图表数据得出:随着x的增大,y相应的也增大;
(3)由图表中数据直接得出:丽丽打了5分钟电话,那么电话费需付3元.
【解答】
解:(1)上表反应的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)根据图表数据得出:随着x的增大,y相应的也增大;
(3)由图表中数据直接得出:丽丽打了5分钟电话,那么电话费需付3元.
24.
【答案】
解:500米、乌龟的速度10米/分等在整个变化过程中是常量,兔子的速度是变量.
【解答】
解:500米、乌龟的速度10米/分等在整个变化过程中是常量,兔子的速度是变量.
25.
【答案】
解:由题意知,开始时A点与M点重合,让正方形MNPQ向左运动,两图形重合的长度为AM=x,
∵ ∠BAC=45?,
∴ S阴影=12×AM×h=12AM2=12x2,
则y=12x2,0其中的常量为等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,变量为重叠部分的面积y与MA的长度x.
【解答】
解:由题意知,开始时A点与M点重合,让正方形MNPQ向左运动,两图形重合的长度为AM=x,
∵ ∠BAC=45?,
∴ S阴影=12×AM×h=12AM2=12x2,
则y=12x2,0其中的常量为等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,变量为重叠部分的面积y与MA的长度x.
26.
【答案】
解:(1)上表反映了刹车速度和刹车距离之间的关系;
(2)根据表格可得:如果刹车时车速为60千米/时,那么刹车距离是7.8米.
【解答】
解:(1)上表反映了刹车速度和刹车距离之间的关系;
(2)根据表格可得:如果刹车时车速为60千米/时,那么刹车距离是7.8米.
班级:_____________姓名:_____________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 人的身高h随时间t的变化而变化,那么下列说法正确的是( )
A.h,t都是不变量 B.t是自变量,h是因变量
C.h,t都是自变量 D.h是自变量,t是因变量?
2. 半径是R的圆的周长C=2πR,下列说法正确的是(? ? ? ? )
A.C,π,R是变量
B.C是变量,2,π,R是常量
C.R是变量,2,π,C是常量
D.C,R是变量,2,π是常量?
3. 在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器的容积?
4. 当圆的半径发生变化时,面积也发生变化,圆面积S与半径r的关系为S=πr2.下面的说法中,正确的是( )
A.S,π,r都是变量 B.只有r是变量
C.S,r是变量,π是常量 D.S,π,r都是常量?
5. 汽车在匀速行驶过程中,路程s、速度v、时间t之间的关系为s=vt,下列说法正确的是(? ? ? ? )
A.s、v、t都是变量?? B.s、t是变量,v是常量
C.v、t是变量,s是常量?? D.s、v是变量,t是常量
?
6. 甲、乙两地相距50千米,若一辆汽车以50千米/时的速度从甲地到乙地,则汽车距乙地的路程s(千米)与行驶的时间t(时)之间的关系式s=50-50t(0≤t≤1)中,常量的个数为( )
A.1个 B.2个 C.3个 D.4个?
7. 如果用总长为60m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为p(m),一边长为a(m),那么S,p,a中是变量的是(? ? ? ? )
A.S和p B.S和a C.p和a D.S,p,a?
8. 以固定的速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动的时间t(秒)之间的关系式是h=v0t-4.9t2,在这个关系式中,常量、变量分别为( )
A.4.9是常量,t,h是变量
B.v0是常量,t,h是变量
C.v0,-4.9是常量,t,h是变量
D.4.9是常量,v0,t,h是变量?
9. 已知圆柱体的高是10厘米,沿着底面直径垂直切开,把圆柱分成相等的两半,表面积增加了40平方厘米,这个圆柱体的体积是( )立方厘米。(全卷π均取3.14)
A.62.8 B.125.6 C.31.4 D.251.2?
10. 弹簧挂上物体会伸长,测得一弹簧的长度x(cm)与所挂的物体的重量y(kg)间的关系如下表:
x
0
1
2
3
4
5
6
y
10
10.5
11
11.5
12
12.5
13
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂物体时的长度为0cm
C.物体质量每增加1kg,弹簧的长度y增加0.5cm
D.所挂的物体的质量为7kg时,弹簧的长度为13.5cm
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. “日落西山”是我们每天都要面对的自然变换,就你的理解,________是自变量,________是因变量. ?
12. 圆的半径为r,圆的面积S与半径r之间有如下关系:S=πr2.在这关系中,常量是________.
13. 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就是说x是________,y是x的________.
14. 一圆锥的底面半径是5cm,当圆锥的高由2cm变到10cm时,圆锥的体积由________cm3变到________cm3.
15. 2B铅笔每枝0.5元,买n枝需W元,其中常量是________,变量是________. ?
16. 每个同学购买一本课本,课本的单价是4.5元,总金额为y(元),学生数为n(个),则变量是________,常量是________. ?
17. 某公司销售部门发现,该公司的销售收入随销售量的变化而变化,在这个变化过程中,自变量是________. ?
18. 在公式s=v0t+2t2(v0为已知数)中,常量是________,变量是________. ?
19. 大家知道,冰层越厚,所承受的压力越大,这其中自变量是________,因变量是________. ?
20. 某公司2020年年终财务报表显示,该公司2020年年终每股净利润为m元.年报公布后的某日,该公司的股票收盘价为x元,所以这天收盘后该股票的市盈率为y=xm,在这三个字母中其中常量是________,变量是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , )
21. 齿轮每分钟120转,如果n表示转数,t表示转动时间.
(1)用n的代数式表示t;
(2)说出其中的变量与常量.
?
22. 设路程为s?km,速度为v?km/h,时间t?h,指出下列各式中的常量与变量.
(1)v=s8;
(2)s=4.5t-2t2;
(3)vt=100.
?
23. 下表是某公共电话亭打长途电话的几次收费记录:
时间(分)
1
2
3
4
5
6
7
电话费(元)
0.6
1.2
1.8
2.4
3.0
3.6
4.2
(1)上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示时间,y表示电话费,那么随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
?
24. 阅读下面这段有关“龟兔赛跑”的寓言故事,并指出所涉及的量中,哪些是常量,哪些是变量.
一次乌龟与兔子举行500米赛跑,比赛开始不久,兔子就遥遥领先.当兔子以20米/分的速度跑了10分时,往回一看,乌龟远远地落在后面呢!兔子心想:“我就是睡一觉,你乌龟也追不上我,我为何不在此美美地睡上一觉呢?”可是,当骄傲的兔子正做着胜利者的美梦时,勤勉的乌龟却从它身边悄悄爬过,并以10米/分的速度匀速爬向终点.40分后,兔子梦醒了,而此时乌龟刚好到达终点.兔子悔之晚矣,等它再以30米/分的速度跑向终点时,它比乌龟足足晚了10分.
?25. 如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积y?cm2与MA的长度x?cm之间的关系式,并指出其中的常量与变量.
?
26. 行驶中的汽车,在刹车后由于惯性的作用,还将继续向前滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能(车速不超过140千米/时),对这种汽车进行测试,测得数据如下表:
刹车时车速
(千米/时)
20
40
60
80
100
120
刹车距离(米)
1.0
3.6
7.8
13.6
21
30
回答下列问题:
(1)上表反映了哪两个变量之间的关系?
(2)如果刹车时车速为60千米/时,那么刹车距离是多少米?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:因为人的身高h随时间t的变化而变化,所以t是自变量,h是因变量;
故本题选B.
2.
【答案】
D
【解答】
解:在某一个变化过程中可以取不同数值的量叫变量,
数值始终不变的量叫常量.
故由常量与变量的定义可得,
在半径是R的圆的周长C=2πR中,
C,R是变量,2,π是常量.
故选D.
3.
【答案】
B
【解答】
解:根据函数的定义可知,水温是随着所晒时间的长短而变化,可知水温是因变量,太阳照晒时间的长短为自变量.
故选B.
4.
【答案】
C
【解答】
解:圆的半径发生变化时,面积也发生变化,圆面积S与半径r的关系为S=πr2,S、r是变量,π是常量,
故选:C.
5.
【答案】
B
【解答】
解:汽车在匀速行驶过程中,速度v不变,是常量,t、s是变量.
故选B.
6.
【答案】
B
【解答】
解:汽车距乙地的路程s(千米)与行驶的时间t(时)之间的关系式s=50-50t(0≤t≤1)中,常量为距离50千米和速度50千米/时两个,
故选B.
7.
【答案】
B
【解答】
解:∵ 篱笆的总长为60米,
∴ 周长p是定值,而面积S和一边长a是变量,
故选B.
8.
【答案】
C
【解答】
解:h=v0t-4.9t2中的v0(米/秒)是固定的速度,-4.9是定值,
故v0和-4.9是常量,t,h是变量,
故选C.
9.
【答案】
C
【解答】
解:设底面圆的半径是r厘米,
根据题意得:10×2×2r=40
解得I=1
∴ 圆柱体积=π×12×10×31.4立方厘米.
故答案为:C.
10.
【答案】
B
【解答】
解:A,y随x的增加而增加,x是自变量,y是因变量,故A选项正确;
B,弹簧不挂重物时的长度为10cm,故B选项错误;
C,物体质量每增加1kg,弹簧长度y增加0.5cm,故C选项正确;
D,由C知,y=10+0.5x,则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故D选项正确.
故选B.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
时间,日落
【解答】
解:“日落西山”是我们每天都要面对的自然变换,就你的理解,时间是自变量,日落是因变量.
故答案是:时间,日落.
12.
【答案】
π
【解答】
解:在S=πr2中π是一个常数(圆周率),即π是常量,S,r是两个变量.
故填π.
13.
【答案】
自变量,函数
【解答】
解:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就是说x是自变量,y是x的函数.
故答案为:自变量,函数.
14.
【答案】
50π3,250π3
【解答】
解圆锥的底面半径是5cm,当圆锥的高由2cm变到10cm时,圆锥的体积由?50π3cm3变到?250π3cm3:,
故答案为:50π3,250π3.
15.
【答案】
0.5,n,W
【解答】
解:铅笔的单价固定,总钱数随着铅笔支数的变化而变化,故常量是0.5,变量是n,W,
故答案为:0.5;n,W.
16.
【答案】
y,n,4.5
【解答】
解:∵ 单价固定,
∴ 常量是4.5,
∵ 总金额为y(元)随着学生数为n(个)的变化而变化,
∴ y,n是变量,
故答案为y,n;4.5.
17.
【答案】
销售量
【解答】
解:该公司的销售收入随销售量的变化而变化,在这个变化过程中,自变量是销售量.
故答案为:销售量.
18.
【答案】
v0,2,s,t
【解答】
解:因为在公式s=v0t+2t2(v0为已知数),所以v0、2是常量,s、t是变量.
19.
【答案】
冰层的厚度,冰层所承受的压力
【解答】
解:大家知道,冰层越厚,所承受的压力越大,这其中自变量是冰层的厚度,因变量是冰层所承受的压力;
故答案为:冰层的厚度,冰层所承受的压力.
20.
【答案】
m,x,y
【解答】
解:y=xm中的三个字母中其中常量是m,变量是x,y,
故答案为:m;x,y.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:(1)由题意得:
120t=n,
t=n120;
(2)变量:t,n常量:120.
【解答】
解:(1)由题意得:
120t=n,
t=n120;
(2)变量:t,n常量:120.
22.
【答案】
解:(1)常量是8,变量是v,s;
(2)常量是4.5,2,变量是s,t;
(3)常量是100,变量是v,t.
【解答】
解:(1)常量是8,变量是v,s;
(2)常量是4.5,2,变量是s,t;
(3)常量是100,变量是v,t.
23.
【答案】
解:(1)上表反应的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)根据图表数据得出:随着x的增大,y相应的也增大;
(3)由图表中数据直接得出:丽丽打了5分钟电话,那么电话费需付3元.
【解答】
解:(1)上表反应的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)根据图表数据得出:随着x的增大,y相应的也增大;
(3)由图表中数据直接得出:丽丽打了5分钟电话,那么电话费需付3元.
24.
【答案】
解:500米、乌龟的速度10米/分等在整个变化过程中是常量,兔子的速度是变量.
【解答】
解:500米、乌龟的速度10米/分等在整个变化过程中是常量,兔子的速度是变量.
25.
【答案】
解:由题意知,开始时A点与M点重合,让正方形MNPQ向左运动,两图形重合的长度为AM=x,
∵ ∠BAC=45?,
∴ S阴影=12×AM×h=12AM2=12x2,
则y=12x2,0
【解答】
解:由题意知,开始时A点与M点重合,让正方形MNPQ向左运动,两图形重合的长度为AM=x,
∵ ∠BAC=45?,
∴ S阴影=12×AM×h=12AM2=12x2,
则y=12x2,0
26.
【答案】
解:(1)上表反映了刹车速度和刹车距离之间的关系;
(2)根据表格可得:如果刹车时车速为60千米/时,那么刹车距离是7.8米.
【解答】
解:(1)上表反映了刹车速度和刹车距离之间的关系;
(2)根据表格可得:如果刹车时车速为60千米/时,那么刹车距离是7.8米.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
