5.3 反比例函数(1)
图片预览






文档简介
(共20张PPT)
5.3反比例函数(第一课时)
教学目标
1.理解反比例函数的概念,会求比例系数.
2.感受反比例函数是刻画世界数量关系的一种有效模型,能够列出实际问题中的反比例函数关系.
3.能依据已知条件确定反比例函数的表达式
写出下列函数关系式
1.当路程 s =10 时,时间 t 与速度 v 的函数关系.
2.当矩形面积 S=5时,长 a 与宽 b 的函数关系.
3.当三角形面积 S =20时,三角形的底边 y 与高 x的函数关系.
请大家观察这几个式子有什么共同特点?
一般地,函数 (k是常数,k≠0)叫做反比例函数,其中x为自变量
反比例函数 ,则 xy=k,k是常数,且k≠0
反比例函数的解析式又可以写成: ( k是常数,k≠0).
正比例函数和反比例函数的比较
请同学们说说它们有哪些不同?
(1)从形式上看,y=kx是关于自变量的整式,反比例函数y= 是关于自变量的分式;
(2)从内涵上看,正比例函数y=kx的两个变量的商是非零常数,即k是常数,且k≠0;反比例函数y= 的两个变量积是一个非零常数;即
xy=k,k是常数,且k≠0.
(3)从自变量和函数值取值范围来看,正比例函数y=kx中的自变量和函数值都可以为零,反比例函数y= 中的自变量和函数值都不能为零。
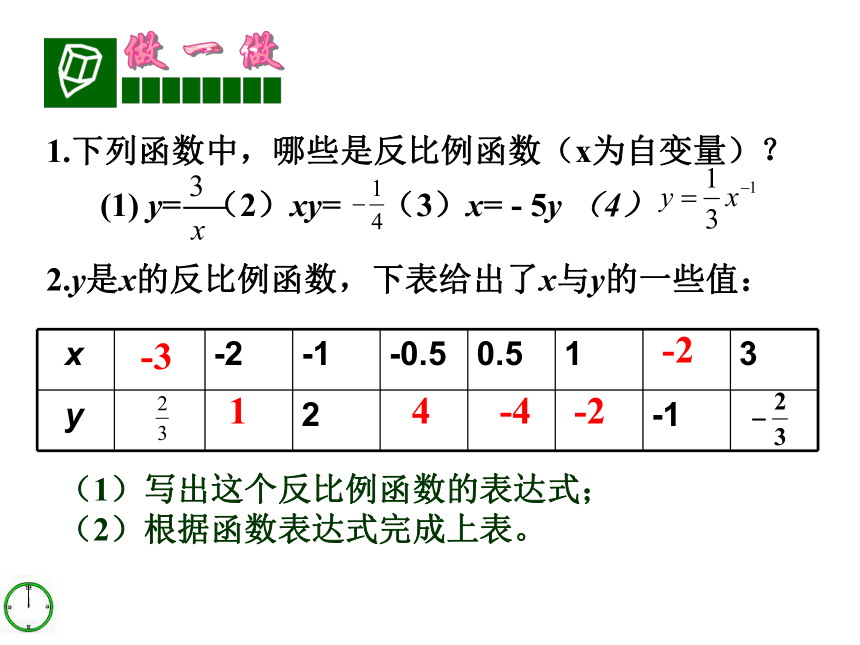
1.下列函数中,哪些是反比例函数(x为自变量)?
(1) y= (2)xy= (3)x= - 5y (4)
2.y是x的反比例函数,下表给出了x与y的一些值:
x -2 -1 -0.5 0.5 1 3
y 2 -1
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表。
-3
1
4
-4
-2
-2
解:(1)设y= .
把x= -1,y=2代入上式,得k= -2.
所以y= .
1.如果一个反比例函数的图象经过点(-2,5),则其解析式为 。
2.若一次函数y=kx+b与反比例函数 的图象的交点是(2,3),则k= ,b= 。
A.(2,-5) B.(-5,-2)
C.(-3,4) D.(4,-3 )
3.已知点(2,5)在反比例函数 的图象上,其中“□”是被污染的无法辨认的字迹,则下列各点在该反比例函数图象上的是( )
y=-10/x
6
-9
B
例3:已知y是x的反比例函数,( , )是它图像上的一点,该图
像是否经过点(-6, )
小结:函数图像上点的坐标都适合这个函数解析式,反过来,坐标适合函数解析式的点都在这个函数的图像上。
反比例函数
定义:
条件:
表达式:
应用:
y=kx-1
(k≠0, k为常数)
考查定义中的条件 k≠0
用待定系数法求反比例函数的表达式(待定系数法一般步骤:1.设,2.代,3.解K,4.写出结论)
一般地,如果两个变量x,y之间的关 系可以表示成:
的形式,那么称y是x的反比例函数.
注意:在实际问题中,自变量的取值还需考虑它的实际意义。
课堂检测
1、如果点(3, 1)在反比例函数 的图象上,求y与x之间的函数关系
2、已知点(2,5)在反比例函数 的图象上,则下列各点在该函数图象上的是( )
A、(2,—5)B、(—5,—2)C、(—3,4) D、(4,—3)
3. y是x的反比例函数,当x=2时,y=3,求y与x之间的函数关系式,并求出当 x=4时,y的值
4(选做))已知y与x-2成反比例,当x=4时,y=3,求当x=5时,y的值.
5.(选做)若 是反比例函数, 求此反比例函数的关系式.
课本P22 A组 T 1. T 2. T 4. T 5.
结 束 语
函数来自现实生活, 函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要数学模型.
同学们,
再见!
5.3反比例函数(第一课时)
教学目标
1.理解反比例函数的概念,会求比例系数.
2.感受反比例函数是刻画世界数量关系的一种有效模型,能够列出实际问题中的反比例函数关系.
3.能依据已知条件确定反比例函数的表达式
写出下列函数关系式
1.当路程 s =10 时,时间 t 与速度 v 的函数关系.
2.当矩形面积 S=5时,长 a 与宽 b 的函数关系.
3.当三角形面积 S =20时,三角形的底边 y 与高 x的函数关系.
请大家观察这几个式子有什么共同特点?
一般地,函数 (k是常数,k≠0)叫做反比例函数,其中x为自变量
反比例函数 ,则 xy=k,k是常数,且k≠0
反比例函数的解析式又可以写成: ( k是常数,k≠0).
正比例函数和反比例函数的比较
请同学们说说它们有哪些不同?
(1)从形式上看,y=kx是关于自变量的整式,反比例函数y= 是关于自变量的分式;
(2)从内涵上看,正比例函数y=kx的两个变量的商是非零常数,即k是常数,且k≠0;反比例函数y= 的两个变量积是一个非零常数;即
xy=k,k是常数,且k≠0.
(3)从自变量和函数值取值范围来看,正比例函数y=kx中的自变量和函数值都可以为零,反比例函数y= 中的自变量和函数值都不能为零。
1.下列函数中,哪些是反比例函数(x为自变量)?
(1) y= (2)xy= (3)x= - 5y (4)
2.y是x的反比例函数,下表给出了x与y的一些值:
x -2 -1 -0.5 0.5 1 3
y 2 -1
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成上表。
-3
1
4
-4
-2
-2
解:(1)设y= .
把x= -1,y=2代入上式,得k= -2.
所以y= .
1.如果一个反比例函数的图象经过点(-2,5),则其解析式为 。
2.若一次函数y=kx+b与反比例函数 的图象的交点是(2,3),则k= ,b= 。
A.(2,-5) B.(-5,-2)
C.(-3,4) D.(4,-3 )
3.已知点(2,5)在反比例函数 的图象上,其中“□”是被污染的无法辨认的字迹,则下列各点在该反比例函数图象上的是( )
y=-10/x
6
-9
B
例3:已知y是x的反比例函数,( , )是它图像上的一点,该图
像是否经过点(-6, )
小结:函数图像上点的坐标都适合这个函数解析式,反过来,坐标适合函数解析式的点都在这个函数的图像上。
反比例函数
定义:
条件:
表达式:
应用:
y=kx-1
(k≠0, k为常数)
考查定义中的条件 k≠0
用待定系数法求反比例函数的表达式(待定系数法一般步骤:1.设,2.代,3.解K,4.写出结论)
一般地,如果两个变量x,y之间的关 系可以表示成:
的形式,那么称y是x的反比例函数.
注意:在实际问题中,自变量的取值还需考虑它的实际意义。
课堂检测
1、如果点(3, 1)在反比例函数 的图象上,求y与x之间的函数关系
2、已知点(2,5)在反比例函数 的图象上,则下列各点在该函数图象上的是( )
A、(2,—5)B、(—5,—2)C、(—3,4) D、(4,—3)
3. y是x的反比例函数,当x=2时,y=3,求y与x之间的函数关系式,并求出当 x=4时,y的值
4(选做))已知y与x-2成反比例,当x=4时,y=3,求当x=5时,y的值.
5.(选做)若 是反比例函数, 求此反比例函数的关系式.
课本P22 A组 T 1. T 2. T 4. T 5.
结 束 语
函数来自现实生活, 函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要数学模型.
同学们,
再见!
