27.1图形的相似
图片预览








文档简介
(共26张PPT)
27.1图形的相似
27.1图形的相似
27.1图形的相似
27.1图形的相似
活动一:创设情境,感知相似
图片欣赏
上述几组图片有什么共同特征?
它们的形状相同,
但大小不一定相等.
观察与思考
形状相同的图形称为相似形。
注意:相似图形的大小不一定相同.
相似图形的概念
相似变换
将图形放大或缩小可以得到相似形.
两两相似的几何图形
相似变换
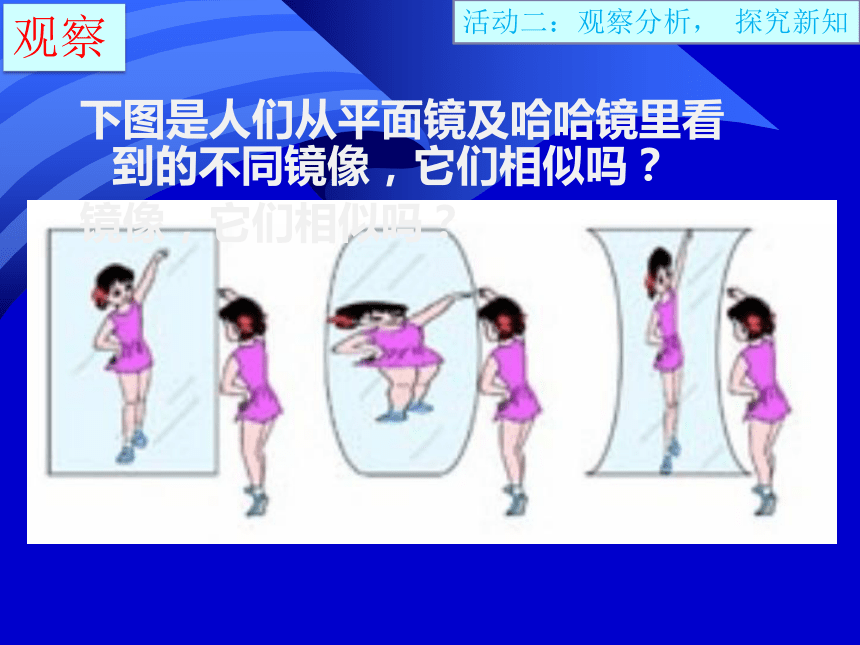
下图是人们从平面镜及哈哈镜里看到的不同镜像,它们相似吗?
镜像,它们相似吗?
活动二:观察分析, 探究新知
观察
我的外边缘有一圈木质边框,他们的宽相等,那么边框的内外边缘所成的矩形相似吗?
我的外边缘有一圈木质边框,他们的宽相等,那么边 框的内外边缘所成的矩形相似吗?
思考
下列两个相似图形,它们的对应角、对应边有怎样的关系?
(1)正三角形ABC与正三角形A1B1C1;
(1)
B
C
A1
B1
C1
A
思考
相似的特征
(2)正方形ABCD与正方形EFGH.
B
C
D
A
(2)
E
F
H
G
思考
相似的特征
下列两个相似图形,它们的对应角、对应边有怎样的关系?
(2)正方形ABCD与正方形EFGH.
解:∵四边形ABCD与四边形EFGH为正方形
∴∠A=∠E= 900, ∠B=∠F= 900
∠C=∠G= 900, ∠D=∠H= 900
AB=BC=CD=DA
EF=FG=GH=HE
∴
E
F
H
G
B
C
D
A
问题: 相似的正六边形,它们的对应角、
对应边有怎样的关系?
相似正多边形各对应角相等、各对应边的比相等.
这个结论对于一般的相似多边形是否成立呢?
1. 下图是两个相似的三角形,猜想它们的对应角、对应边的比是否相等?
探究
2. 对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?
问题:任意两个相似的多边形有什么性质
活动三:合作探究,归纳结论
相似多边形性质:
相似多边形对应角相等,对应边的比相等.
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.
相似多边形的判定方法:
归纳
我们把相似多边形对应边的比称为相似比.
两图形全等
相似比为1时,相似的两个图形有什么关系?
归纳
我是长3m,宽1.5m的矩形黑板.镶在我外围的木质边框宽10cm ,边框的内外边缘所成的矩形相似吗?为什么?
它们不相似,因为对应边的比不相等.
长3米
宽1.5米
活动四:新知应用,加深理解
例、 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
24
G
E
F
H
α
x
118°
D
A
B
C
18
21
78°
83°
β
活动四:新知应用,加深理解
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠C=∠α=83°,∠A=∠E=118°
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得
解得 x=28
1. 在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离.
设两地的实际距离为xcm
x = 300000000
x = 3000千米
答: 甲,乙两地的实际距离为3000千米
解:
巩固新知
2. 如图所示的两个三角形一定相似吗?
为什么?
10
5
5
10
不 一 定 相 似
3. 如图所示的两个五边形相似,求未知边a、b、
c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示: 可知两图形的相似比为:
∴
b = 4.5
a = 3
c = 4
d = 6
通过本节课的学习,
你有哪些收获?
活动五:内化探究 知识升华
谈谈收获
A B D F
请用你所学的知识解决下列问题:
活动五:内化探究 知识升华
27.1图形的相似
27.1图形的相似
27.1图形的相似
27.1图形的相似
活动一:创设情境,感知相似
图片欣赏
上述几组图片有什么共同特征?
它们的形状相同,
但大小不一定相等.
观察与思考
形状相同的图形称为相似形。
注意:相似图形的大小不一定相同.
相似图形的概念
相似变换
将图形放大或缩小可以得到相似形.
两两相似的几何图形
相似变换
下图是人们从平面镜及哈哈镜里看到的不同镜像,它们相似吗?
镜像,它们相似吗?
活动二:观察分析, 探究新知
观察
我的外边缘有一圈木质边框,他们的宽相等,那么边框的内外边缘所成的矩形相似吗?
我的外边缘有一圈木质边框,他们的宽相等,那么边 框的内外边缘所成的矩形相似吗?
思考
下列两个相似图形,它们的对应角、对应边有怎样的关系?
(1)正三角形ABC与正三角形A1B1C1;
(1)
B
C
A1
B1
C1
A
思考
相似的特征
(2)正方形ABCD与正方形EFGH.
B
C
D
A
(2)
E
F
H
G
思考
相似的特征
下列两个相似图形,它们的对应角、对应边有怎样的关系?
(2)正方形ABCD与正方形EFGH.
解:∵四边形ABCD与四边形EFGH为正方形
∴∠A=∠E= 900, ∠B=∠F= 900
∠C=∠G= 900, ∠D=∠H= 900
AB=BC=CD=DA
EF=FG=GH=HE
∴
E
F
H
G
B
C
D
A
问题: 相似的正六边形,它们的对应角、
对应边有怎样的关系?
相似正多边形各对应角相等、各对应边的比相等.
这个结论对于一般的相似多边形是否成立呢?
1. 下图是两个相似的三角形,猜想它们的对应角、对应边的比是否相等?
探究
2. 对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?
问题:任意两个相似的多边形有什么性质
活动三:合作探究,归纳结论
相似多边形性质:
相似多边形对应角相等,对应边的比相等.
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.
相似多边形的判定方法:
归纳
我们把相似多边形对应边的比称为相似比.
两图形全等
相似比为1时,相似的两个图形有什么关系?
归纳
我是长3m,宽1.5m的矩形黑板.镶在我外围的木质边框宽10cm ,边框的内外边缘所成的矩形相似吗?为什么?
它们不相似,因为对应边的比不相等.
长3米
宽1.5米
活动四:新知应用,加深理解
例、 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
24
G
E
F
H
α
x
118°
D
A
B
C
18
21
78°
83°
β
活动四:新知应用,加深理解
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠C=∠α=83°,∠A=∠E=118°
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得
解得 x=28
1. 在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离.
设两地的实际距离为xcm
x = 300000000
x = 3000千米
答: 甲,乙两地的实际距离为3000千米
解:
巩固新知
2. 如图所示的两个三角形一定相似吗?
为什么?
10
5
5
10
不 一 定 相 似
3. 如图所示的两个五边形相似,求未知边a、b、
c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示: 可知两图形的相似比为:
∴
b = 4.5
a = 3
c = 4
d = 6
通过本节课的学习,
你有哪些收获?
活动五:内化探究 知识升华
谈谈收获
A B D F
请用你所学的知识解决下列问题:
活动五:内化探究 知识升华
