人教版七年级数学 下册 第五章 5.1.1 相交线 课件(共43张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第五章 5.1.1 相交线 课件(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览







文档简介
(共43张PPT)
导入新课
问题:剪刀两个把手之间的角发生了什么变化?剪刀张开的口又怎么变化?
如果将剪刀的构造看作两条相交的直线,这就关系到两条直线所成的角的问题.
5.1.1
相交线
人教版七年级数学
下册
学习目标:
1、理解邻补角、对顶角的意义。
2、理解并掌握对顶角的性质及其推理过程。
3、能够灵活运用邻补角和对顶角的意义和性质解决相关问题。
自主学习
阅读课本内容,思考并完成:
1、同一平面内,如果两条直线相交叉,会形成几个小于平角的角?
2、探究第2页“探究”,∠1,∠2,∠3,∠4分别存在怎样的位置关系和数量关系?
3、说一说互为邻补角的两个角有什么具体特征?
4、什么样的两个角互为对顶角?
5、掌握对顶角的性质,理解这个性质推理过程。
6、理解第3页“例1”的解题方法。
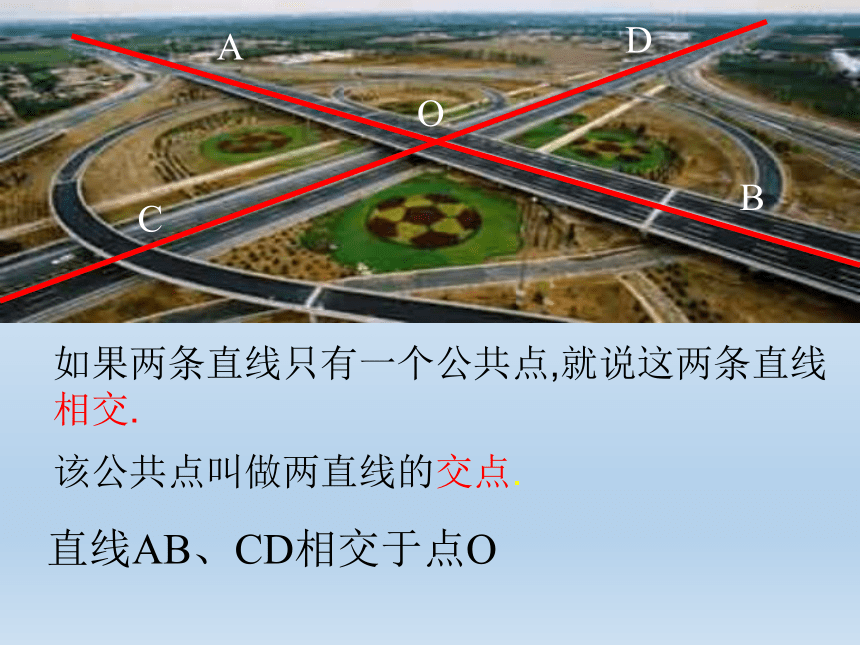
观察下列图片,说一说直线与直线的位置关系.
相交线和平行线是我们日常生活和生产中经常见到的,研究它们对今后的学习、工作和生活都很有用。
我们先来研究相交线。
直线与直线相交于一点,并形成了四个角.
你发现了什么?
A
B
C
D
O
直线AB、CD相交于点O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点.
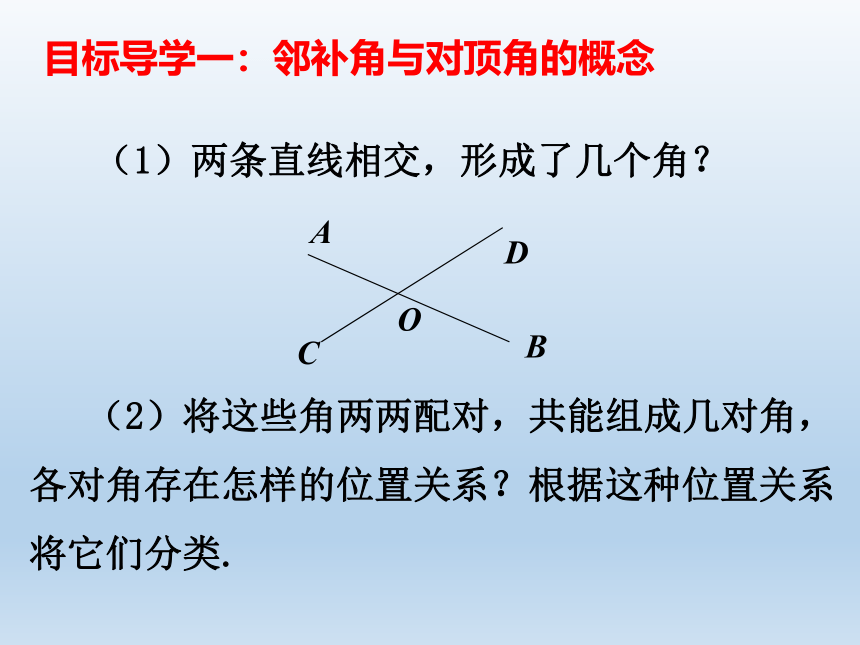
(1)两条直线相交,形成了几个角?
O
C
A
B
D
(2)将这些角两两配对,共能组成几对角,各对角存在怎样的位置关系?根据这种位置关系将它们分类.
目标导学一:邻补角与对顶角的概念
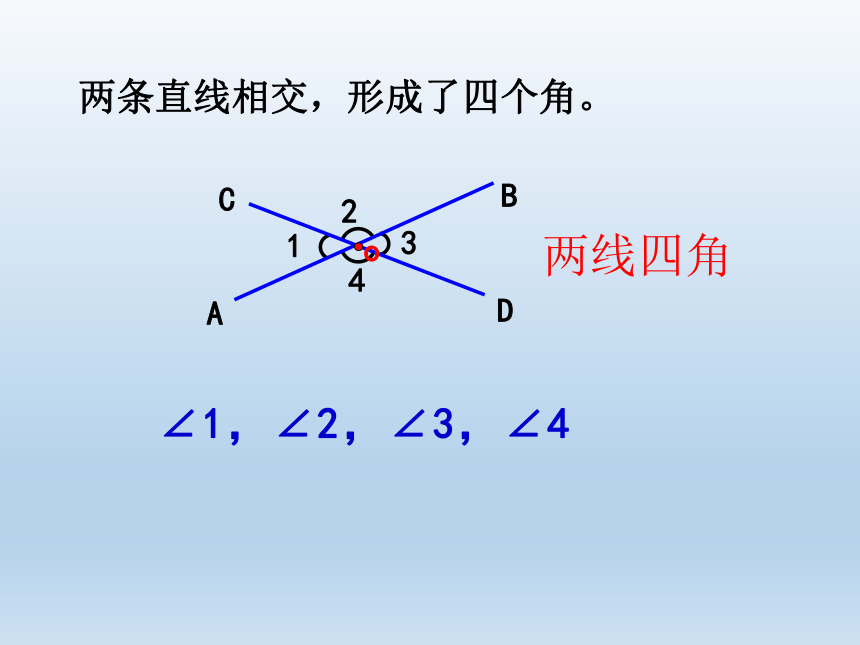
∠1,∠2,∠3,∠4
1
2
3
4
B
A
C
D
o
两线四角
两条直线相交,形成了四个角。
1
2
A
C
D
O
3
4
B
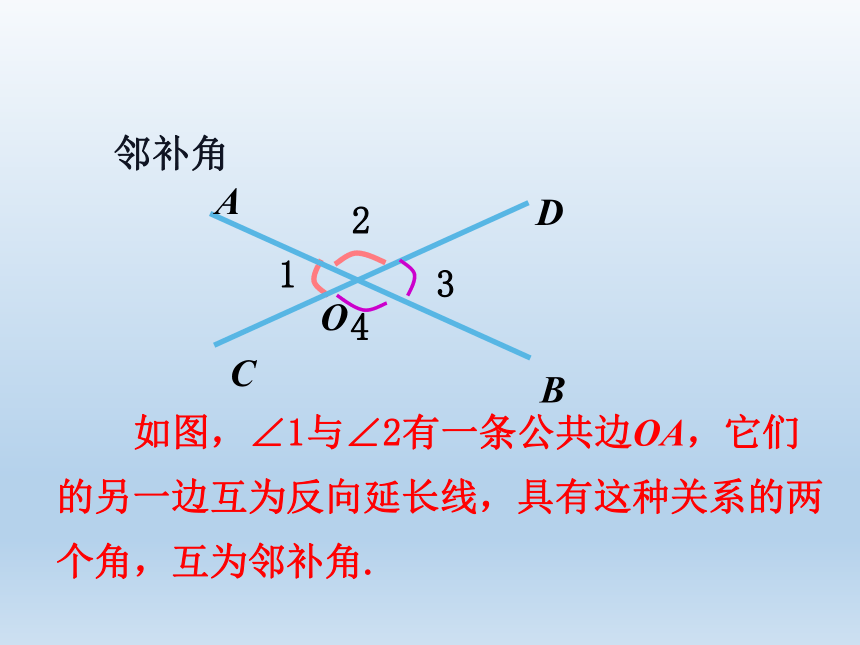
如图,∠1与∠2有一条公共边OA,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
邻补角
邻补角
1
2
3
A
B
C
D
O
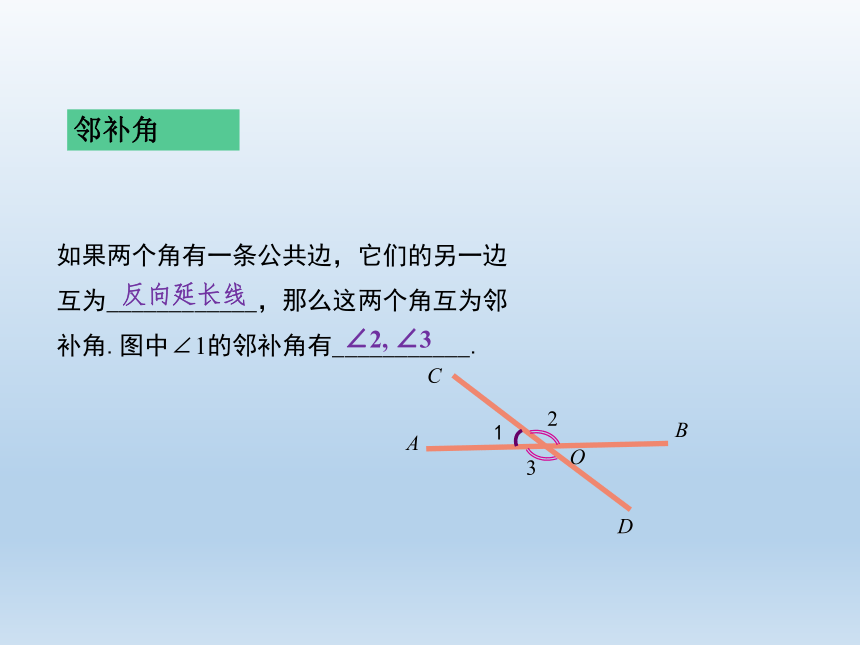
如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
反向延长线
∠2,
∠3
1
2
A
C
D
O
3
4
B
思
考
问题:
∠1
与∠2、∠2与
∠3
、∠3与
∠4、
∠4与
∠1分别有何联系?
1.有一条公共边
2.角的另一边互为反向延长线.
邻补角
1
2
A
C
D
O
3
4
B
如图,∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种关系的两个角,互为对顶角.
对顶角
对顶角
1
2
A
B
C
D
O
对顶角的概念:如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的
,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠2
对顶角
1.顶点相同.
2.角的两边互为反向延长线.
B
A
O
C
D
1
2
两条直线相交出现对顶角
对顶角是成对出现的
例1
下列各图中,∠1与∠2是对顶角的是(
)
1
2
C
1
2
D
D
1
2
A
1
2
B
方法总结:对顶角是由两条相交直线构成的,
只有两条直线相交时,才能构成对顶角.
典例精析
1.下列各图中,∠1和∠2是邻补角吗?为什么?
(1)
(2)
(3)
1
2
1
1
2
2
即学即练
例2:如图,三条直线相交于一点O,说出图中所有对顶角。
A
B
C
D
E
F
O
E
A
B
C
D
O
C
D
F
O
A
B
E
F
O
图中共有几组对顶角?
A
B
C
即学即练
(1)对顶角相等
(
)
(2)相等的角是对顶角(
)
(3)若两个角不相等,则这两个角一定不是对顶
角。(
)
(4)若这两个角不是对顶角,则这两个角不相等。(
)
(5)有公共顶点,并且相等的角是对顶角(
)
(6)两条直线相交,有公共顶点的角是对顶角(
)
Y
N
N
N
N
Y
请你判断
对顶角相等
想一想:下图中是对顶角量角器,你能说出用它测量角的度数的原理吗?
猜想:对顶角相等
C
O
A
B
D
4
3
2
1
问题:∠1
与∠3在数量上又有什么关系呢?
思考:你能利用有关知识来验证∠1
与∠3的数量关系吗?
在上学期我们已经知道互为补角的两个角的和为180°,因而互为邻补角的两个角的和为180°.
目标导学二:邻补角与对顶角的性质
1
2
A
C
D
O
3
4
B
因为∠1与∠2互补,
∠3与∠2互补,
所以∠1=∠3.
类似地,
∠2=∠4.
推出性质
∠1与∠2有怎样的数量关系?
A
B
C
D
O
1
2
3
4
互
补
1
2
如图,直线a,b相交,∠1=40°,求∠2,∠3,
∠4的度数.
3
4
a
b
解:因为∠1+∠2=180°(邻补角的定义),
所以∠2=180°-∠1=180°-
40°=140°;
由对顶角相等,得∠3=∠1=40°,
∠4=∠2=140°.
推出性质
你能说出∠1=∠3的道理吗?
因为
∠1与∠2
互补,
∠3与∠2
互补
(邻补角的定义),
所以
∠1=∠3(同角的补角相等),
同理
∠2=∠4
.
A
B
C
D
O
1
2
3
4
请你用数学的语言写出这个过程.
数量关系
B
A
C
D
O
1
2
3
4
1.有公共顶点
归类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1.有公共顶点
特征
邻补角
对顶角
2.有一条公共边
3.另一边互为反向
延长线
2.没有公共边
两直线相交
3.两边互为反向延长线
位置关系
知识小结
邻补角、对顶角的位置关系和大小关系
∠1+∠2=
∠2+∠3=
∠3+∠4=
∠4+∠1=
∠1=∠3
∠2=∠4
a
b
)
(
1
3
4
2
)
(
例3:如图,直线a、b相交,∠1=40°,求
∠2、∠3、∠4的度数。
∵∠3=∠1
∠1=40°
∴∠3=40°
解:
∴∠2=180°-∠1=140°
∴∠4=∠2=140°
变式训练:
如图,直线a、b相交,若∠2是∠1的3倍,求∠3的度数?
用代数的方法(列方程)解决几何问题是比较有效的!
1.如图,直线AB、CD
相交于点O,∠AOE=90°,如果∠1=20°,那么∠2=______,∠3=______,∠4=______.
20°
70°
160°
即学即练
如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.你能说出其中的一些邻补角与对顶角吗?两根木条所成的角中,如果∠α=35°,其他三个角各等于多少度?如果∠α等于90°,115°,m°呢?
解:若∠α
=35°,其他三个角分别为:145°,35°,145°.
若∠α
=90°,其他三个角分别为:90°,90°,90°.
若∠α
=115°,其他三个角分别为:65°,115°,65°.
若∠α
=m°,其他三个角分别为:(180-m)°,m°,
(180-m)°.
即学即练
图形语言(基本图形)
文字语言
符号语言
邻补角
对顶角
对顶角相等
∵∠1与∠3是对顶角
∴∠1=∠3
(对顶角相等)
)
(
1
3
(
1
2
(
三种语言
在下图中,花坛转角按图纸要求这个角(红色标注的角)为135°;施工结束后,要求你检测它是否合格?请你设计检测的方法.
A
D
B
C
O
∠AOB=
∠AOC(邻补角定义)
∠AOB=
∠BOD(邻补角定义)
∠
AOB
=∠COD(对顶角相等)
转化思想
联系生活
教师寄语
今天,我们学习了两直线相交这种位置关系的有关知识,要弄清对顶角和邻补角这两个重要概念以及“对顶角相等”这一重要性质,因为它们在我们今后的学习中经常用到;要学会从复杂的图形中分解出基本的图形,从而正确识别对顶角、邻补角,逐步训练和提高自己的识图能力和计算推理能力。
知识
两直线的位置关系
相交
平行
位置关系
对顶角
邻补角
数量关系
相等
互补
过程与方法
观察
思考
探究
数学思想
方程思想
转化思想
类比思想
课堂小结
谈谈本节课的收获
1.下列各图中,
∠1
,∠2是对顶角吗?
(
)
1
2
(
)
1
2
(
)
2
1
2.下列各图中,
∠1
,∠2是邻补角吗?
(
1
(
2
(
)
1
2
(
)
1
2
不是
是
不是
不是
是
不是
检测目标
3、如图,三条直线l1,l2,l3交于点O,求
1+
3+
5
等于多少?
l1
l2
l3
o
1
3
2
6
5
4
检测目标
4.观察下列各图,寻找对顶角(不含平角)
⑴
如图a,图中共有
对对顶角;
⑵
如图b,图中共有
对对顶角;
⑶
如图c,图中共有
对对顶角;
⑷
研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸
若有10条直线相交于一点,则可形成
对对顶角.
图a
图b
图c
2
6
12
n(n-1)
90
转化思想
转化成两条直线相交
检测目标
5.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
解:(1)∠BOE=180°-∠AOC-∠COE=180°-36°-90°=54°.
(2)因为∠BOD∶∠BOC=1∶5,∠BOD+∠BOC=180°,
所以∠BOD=30°.
因为∠AOC=∠BOD,
所以∠AOC=30°,
所以∠AOE=∠COE+∠AOC=90°+30°=120°.
检测目标
6.
(应用题)在下图中,花坛转角(红色标注的角)按图纸要求为135°;施工结束后,要求你检测它是否合格?请你设计检测的方法.
1
2
解:方法一:
检测∠1是否为45°;
方法二:
检测∠2是否为135°.
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
导入新课
问题:剪刀两个把手之间的角发生了什么变化?剪刀张开的口又怎么变化?
如果将剪刀的构造看作两条相交的直线,这就关系到两条直线所成的角的问题.
5.1.1
相交线
人教版七年级数学
下册
学习目标:
1、理解邻补角、对顶角的意义。
2、理解并掌握对顶角的性质及其推理过程。
3、能够灵活运用邻补角和对顶角的意义和性质解决相关问题。
自主学习
阅读课本内容,思考并完成:
1、同一平面内,如果两条直线相交叉,会形成几个小于平角的角?
2、探究第2页“探究”,∠1,∠2,∠3,∠4分别存在怎样的位置关系和数量关系?
3、说一说互为邻补角的两个角有什么具体特征?
4、什么样的两个角互为对顶角?
5、掌握对顶角的性质,理解这个性质推理过程。
6、理解第3页“例1”的解题方法。
观察下列图片,说一说直线与直线的位置关系.
相交线和平行线是我们日常生活和生产中经常见到的,研究它们对今后的学习、工作和生活都很有用。
我们先来研究相交线。
直线与直线相交于一点,并形成了四个角.
你发现了什么?
A
B
C
D
O
直线AB、CD相交于点O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点.
(1)两条直线相交,形成了几个角?
O
C
A
B
D
(2)将这些角两两配对,共能组成几对角,各对角存在怎样的位置关系?根据这种位置关系将它们分类.
目标导学一:邻补角与对顶角的概念
∠1,∠2,∠3,∠4
1
2
3
4
B
A
C
D
o
两线四角
两条直线相交,形成了四个角。
1
2
A
C
D
O
3
4
B
如图,∠1与∠2有一条公共边OA,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
邻补角
邻补角
1
2
3
A
B
C
D
O
如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
反向延长线
∠2,
∠3
1
2
A
C
D
O
3
4
B
思
考
问题:
∠1
与∠2、∠2与
∠3
、∠3与
∠4、
∠4与
∠1分别有何联系?
1.有一条公共边
2.角的另一边互为反向延长线.
邻补角
1
2
A
C
D
O
3
4
B
如图,∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种关系的两个角,互为对顶角.
对顶角
对顶角
1
2
A
B
C
D
O
对顶角的概念:如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的
,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠2
对顶角
1.顶点相同.
2.角的两边互为反向延长线.
B
A
O
C
D
1
2
两条直线相交出现对顶角
对顶角是成对出现的
例1
下列各图中,∠1与∠2是对顶角的是(
)
1
2
C
1
2
D
D
1
2
A
1
2
B
方法总结:对顶角是由两条相交直线构成的,
只有两条直线相交时,才能构成对顶角.
典例精析
1.下列各图中,∠1和∠2是邻补角吗?为什么?
(1)
(2)
(3)
1
2
1
1
2
2
即学即练
例2:如图,三条直线相交于一点O,说出图中所有对顶角。
A
B
C
D
E
F
O
E
A
B
C
D
O
C
D
F
O
A
B
E
F
O
图中共有几组对顶角?
A
B
C
即学即练
(1)对顶角相等
(
)
(2)相等的角是对顶角(
)
(3)若两个角不相等,则这两个角一定不是对顶
角。(
)
(4)若这两个角不是对顶角,则这两个角不相等。(
)
(5)有公共顶点,并且相等的角是对顶角(
)
(6)两条直线相交,有公共顶点的角是对顶角(
)
Y
N
N
N
N
Y
请你判断
对顶角相等
想一想:下图中是对顶角量角器,你能说出用它测量角的度数的原理吗?
猜想:对顶角相等
C
O
A
B
D
4
3
2
1
问题:∠1
与∠3在数量上又有什么关系呢?
思考:你能利用有关知识来验证∠1
与∠3的数量关系吗?
在上学期我们已经知道互为补角的两个角的和为180°,因而互为邻补角的两个角的和为180°.
目标导学二:邻补角与对顶角的性质
1
2
A
C
D
O
3
4
B
因为∠1与∠2互补,
∠3与∠2互补,
所以∠1=∠3.
类似地,
∠2=∠4.
推出性质
∠1与∠2有怎样的数量关系?
A
B
C
D
O
1
2
3
4
互
补
1
2
如图,直线a,b相交,∠1=40°,求∠2,∠3,
∠4的度数.
3
4
a
b
解:因为∠1+∠2=180°(邻补角的定义),
所以∠2=180°-∠1=180°-
40°=140°;
由对顶角相等,得∠3=∠1=40°,
∠4=∠2=140°.
推出性质
你能说出∠1=∠3的道理吗?
因为
∠1与∠2
互补,
∠3与∠2
互补
(邻补角的定义),
所以
∠1=∠3(同角的补角相等),
同理
∠2=∠4
.
A
B
C
D
O
1
2
3
4
请你用数学的语言写出这个过程.
数量关系
B
A
C
D
O
1
2
3
4
1.有公共顶点
归类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1.有公共顶点
特征
邻补角
对顶角
2.有一条公共边
3.另一边互为反向
延长线
2.没有公共边
两直线相交
3.两边互为反向延长线
位置关系
知识小结
邻补角、对顶角的位置关系和大小关系
∠1+∠2=
∠2+∠3=
∠3+∠4=
∠4+∠1=
∠1=∠3
∠2=∠4
a
b
)
(
1
3
4
2
)
(
例3:如图,直线a、b相交,∠1=40°,求
∠2、∠3、∠4的度数。
∵∠3=∠1
∠1=40°
∴∠3=40°
解:
∴∠2=180°-∠1=140°
∴∠4=∠2=140°
变式训练:
如图,直线a、b相交,若∠2是∠1的3倍,求∠3的度数?
用代数的方法(列方程)解决几何问题是比较有效的!
1.如图,直线AB、CD
相交于点O,∠AOE=90°,如果∠1=20°,那么∠2=______,∠3=______,∠4=______.
20°
70°
160°
即学即练
如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.你能说出其中的一些邻补角与对顶角吗?两根木条所成的角中,如果∠α=35°,其他三个角各等于多少度?如果∠α等于90°,115°,m°呢?
解:若∠α
=35°,其他三个角分别为:145°,35°,145°.
若∠α
=90°,其他三个角分别为:90°,90°,90°.
若∠α
=115°,其他三个角分别为:65°,115°,65°.
若∠α
=m°,其他三个角分别为:(180-m)°,m°,
(180-m)°.
即学即练
图形语言(基本图形)
文字语言
符号语言
邻补角
对顶角
对顶角相等
∵∠1与∠3是对顶角
∴∠1=∠3
(对顶角相等)
)
(
1
3
(
1
2
(
三种语言
在下图中,花坛转角按图纸要求这个角(红色标注的角)为135°;施工结束后,要求你检测它是否合格?请你设计检测的方法.
A
D
B
C
O
∠AOB=
∠AOC(邻补角定义)
∠AOB=
∠BOD(邻补角定义)
∠
AOB
=∠COD(对顶角相等)
转化思想
联系生活
教师寄语
今天,我们学习了两直线相交这种位置关系的有关知识,要弄清对顶角和邻补角这两个重要概念以及“对顶角相等”这一重要性质,因为它们在我们今后的学习中经常用到;要学会从复杂的图形中分解出基本的图形,从而正确识别对顶角、邻补角,逐步训练和提高自己的识图能力和计算推理能力。
知识
两直线的位置关系
相交
平行
位置关系
对顶角
邻补角
数量关系
相等
互补
过程与方法
观察
思考
探究
数学思想
方程思想
转化思想
类比思想
课堂小结
谈谈本节课的收获
1.下列各图中,
∠1
,∠2是对顶角吗?
(
)
1
2
(
)
1
2
(
)
2
1
2.下列各图中,
∠1
,∠2是邻补角吗?
(
1
(
2
(
)
1
2
(
)
1
2
不是
是
不是
不是
是
不是
检测目标
3、如图,三条直线l1,l2,l3交于点O,求
1+
3+
5
等于多少?
l1
l2
l3
o
1
3
2
6
5
4
检测目标
4.观察下列各图,寻找对顶角(不含平角)
⑴
如图a,图中共有
对对顶角;
⑵
如图b,图中共有
对对顶角;
⑶
如图c,图中共有
对对顶角;
⑷
研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸
若有10条直线相交于一点,则可形成
对对顶角.
图a
图b
图c
2
6
12
n(n-1)
90
转化思想
转化成两条直线相交
检测目标
5.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
解:(1)∠BOE=180°-∠AOC-∠COE=180°-36°-90°=54°.
(2)因为∠BOD∶∠BOC=1∶5,∠BOD+∠BOC=180°,
所以∠BOD=30°.
因为∠AOC=∠BOD,
所以∠AOC=30°,
所以∠AOE=∠COE+∠AOC=90°+30°=120°.
检测目标
6.
(应用题)在下图中,花坛转角(红色标注的角)按图纸要求为135°;施工结束后,要求你检测它是否合格?请你设计检测的方法.
1
2
解:方法一:
检测∠1是否为45°;
方法二:
检测∠2是否为135°.
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
