人教版七年级数学 下册 第五章 5.2.1 平行线 课件(共47张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第五章 5.2.1 平行线 课件(共47张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览







文档简介
(共47张PPT)
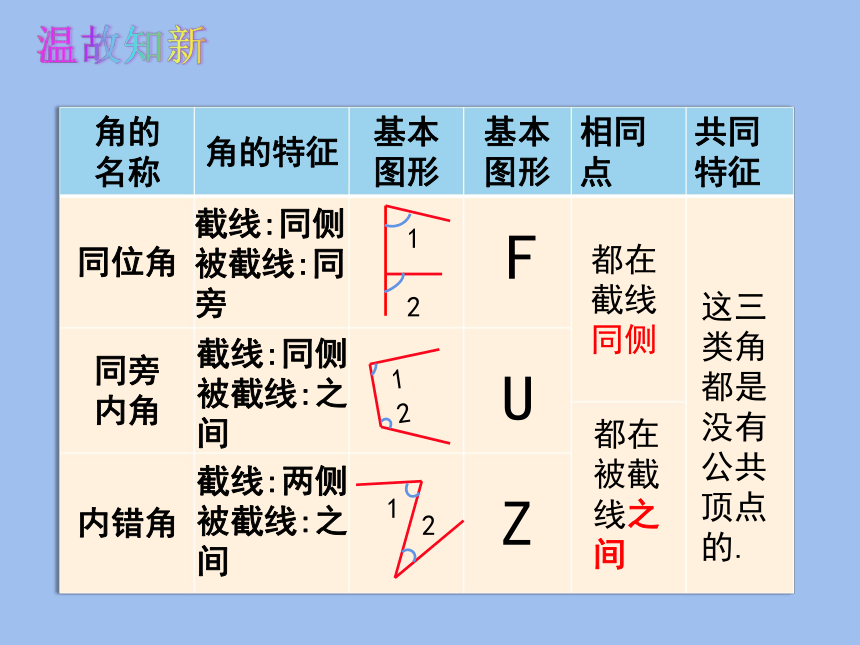
温故知新
1.什么是同位角?有何特征?
2.什么是同旁内角?有何特征?
3.什么是内错角?有何特征?
角的
名称
角的特征
基本图形
基本图形
相同点
共同特征
同位角
同旁
内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
温故知新
导入新课
我们学习了“三线八角”,侧重从角的角度探究;那么,两条直线的位置关系,又有哪几种情况呢?
5.2.1
平
行
线
人教版七年级数学
下册
学习目标:
1.了解平行线的概念,知道同一平面内不重合的两条直线的两种位置关系,
能叙述平行公理以及平行公理的推论.
2.会用符号语言表示平行公理及其推论,
会用三角尺和直尺过已知直线外一点画这条直线的平行线.
学习重、难点:
重点:平行公理及其推论.
难点:文字语言、图形语言、符号语言的
相互转换.
生活中的平行线
如图,直线
a、b
是铁路上的两条铁轨,它们会相交吗?今天我们就来研究这样的两条直线——平行线.
a
b
思考:如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
a
b
c
a
b
c
a
b
c
目标导学一:平行线的定义及表示
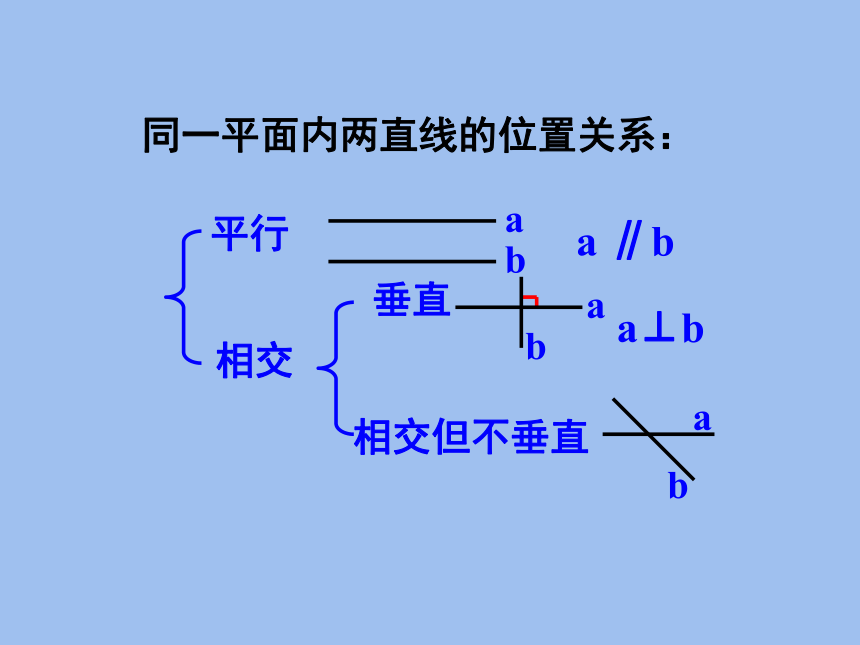
同一平面内两直线的位置关系:
平行
相交
垂直
相交但不垂直
a
b
a⊥b
a
∥b
a
b
b
a
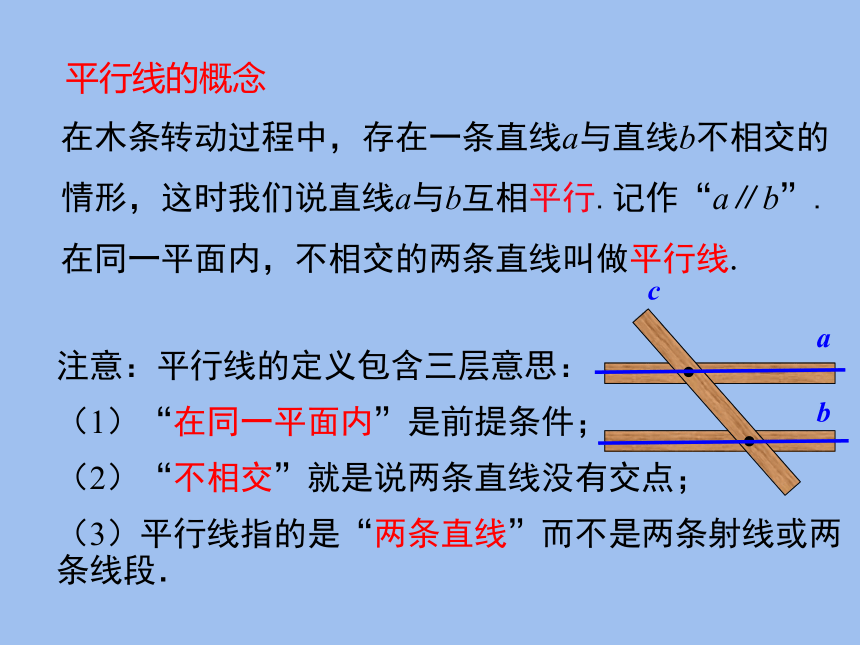
在木条转动过程中,存在一条直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作“a∥b”.
在同一平面内,不相交的两条直线叫做平行线.
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是“两条直线”而不是两条射线或两条线段.
平行线的概念
a
b
c
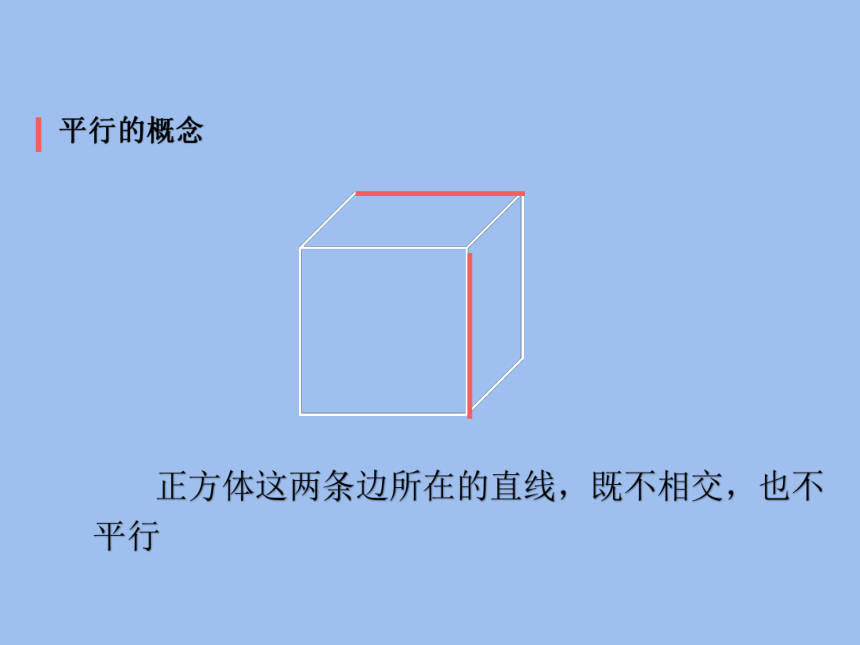
正方体这两条边所在的直线,既不相交,也不平行
平行的概念
平行线的理解
【问题1】在同一平面内,两条不重合的直线有几种位置关系呢?
【问题2】不相交的两条直线一定是平行吗?
相交
平行
不一定
在同一平面内,两直线的位置关系有平行与相交两种。
A
D
B
C
a
b
记作:AB∥CD
读作:直线AB平行于直线CD
记作:a∥b
读作:直线a平行于直线b
一般,我们用“∥”这个符号表示平行
平行线的几何语言:
例:观察如图所示的长方体后填空:
(1)用符号表示下列两棱的位置关系:
A1B1
AB,
AA1
AB,
A1D1
C1D1,
AD
BC。
(2)
A1B1与BC所在的直线是两条不
相交的直线,他们
平行。
(填“是”或“不是”),
由此可知,在
内,两条
不相交的直线才能叫做平行线。
∥
∥
⊥
⊥
同一平面
C
B
D
B1
A1
A
C1
D1
不是
你能举出一些平行线的例子吗?
黑
板
跑道
游泳池
各国国旗
俄罗斯
马来西亚
泰国
探究与思考
给一条直线a,你能画出直线a的平行线吗?
a
b
平行线的画法
:一放、二靠、三推、四画。
目标导学二:平行线的画法、平行公理及其推论
探究与思考
过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?
a
B
C
b
c
探究与思考
尺子的摆放只有这一种吗,换一种方法过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?
a
B
C
b
c
请按图所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法中,三角板起着什么作用?
(2)
把图中的直线
,
看成被尺边AB所截,那么在画图过程中,什么角始终保持相等?由此你能发现画两直线平行方法的依据吗?
想一想!
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践
平行公理:经过直线外一点,有且只有一条直线与已知
直线平行.
·
A
·
B
·
·
C
D
a
b
由以上的实践你发现了什么?
说说看
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
平行公理
经过直线外一点,有且只有一条直线与这条直线平行.?
a
b
直线上就不行
存在且唯一
如图:三条直线a、b、c。如果a//c,b//c,
那么直线a与b有什么关系?
F
E
b
a
假设a与b相交,
设a与b相交于O
因为a//c,b//c
于是过点O就有两条直线a,b都与c平行。
根据平行公理,这是不可能的
也就是说,a与b不能相交,
只能平行。
O
c
平行公理的推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
平行线具有传递性.
b
a
c
因为
b∥a,c
∥a,
所以
b∥c.
几何语言表达:
c
b
a
平行公理的推论(平行线的传递性):
∵a//c
,
c//b(已知)
?
a//b(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
平行线的两条性质:
平面内,经过直线外一点,有且只有一条直线与这条直线平行.
①平行公理:
(唯一性)
②推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
(平行线的传递性)
如果b∥a,
c∥a,
那么b∥c.
例:完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB
//
DE,BC
//
DE(已知)。所以
A,B,C三点___________(
)
(2)如图2所示,因为AB
//
CD,CD
//
EF(已知),所以
________
//
_________(
)
·
·
·
A
D
E
B
C
图
1
A
B
C
D
E
F
图
2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
如图,直线a
∥b,b∥c,c∥d,那么a
∥d吗?为什么?
a
b
c
d
解:
因为
a
∥b,b∥c,
所以
a
∥c
(
)
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为
c∥d,
所以
a
∥d
(
)
能力拓展
平行线
平行线的定义和画法
平行公理及其推导
定义
画法
平行公理
推论
一落;二靠;三移;四画
a
P
b
c
如果b∥a,c∥a,那么b∥c.
课堂小结
判断下列说法是否正确,并说明理由.?
不相交的两条直线是平行线.
在同一平面内,两条不相交的线段是平行线.
过一点可以而且只可以画一条直线与已知直线平行.
(
)
(
)
(
)
检测目标
①
过两点有且只有一条直线.
②
两条不同的直线有且只有一个公共点.
③
过一点有且只有一条直线与己知直线垂直。
④
过一点有且只有一条直线与己知直线平行。
(A)1
(B)
2
(C)3 (D)4
在同一平面内,下列说法中,正确的有(
)个.
√
×
√
×
B
检测目标
下列推理正确的是(
)
A、因为a
//
d,b
//
c,所以c
//
d;
B、因为a
//
c,b
//
d,所以c
//
d;
C、因为a
//
b,a
//
c,所以b
//
c;
D、因为a
//
b,c
//
d,所以a
//
c。
C
检测目标
下列说法中正确的是(
)
A.两条相交的直线叫做平行线
B.如果a∥b,b∥c,则a不与c平行
C.在直线外一点,只能画出一条直线与已知直线平行
D.两条不平行的射线,在同一平面内一定相交
【详解】
A.在同一平面内,不相交的两条直线叫平行线,故本选项错误;
B.如果a∥b,b∥c,则a与c平行,故本选项错误;
C.在直线外一点,只能画出一条直线与已知直线平行,故本选项正确;
D.两条不平行的射线,在同一平面内不一定相交,故本选项错误;故选:C.
检测目标
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行
下列说法正确的是(
)
检测目标
在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A.1cm
B.3cm
C.5cm或3cm
D.1cm或3cm
【答案】C
【解析】详解:当直线c在a、b之间时,
∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4-1=3(cm);
当直线c不在a、b之间时,
∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4+1=5(cm),
综上所述,a与c的距离为3cm或5cm.故选:C.
检测目标
下列说法正确的是(
)
A、在同一平面内,两条直线的位置关系有相交,垂直,平行三种。
B、在同一平面内,不垂直的两直线必平行。
C、在同一平面内,不平行的两直线必垂直。
D、在同一平面内,不相交的两直线一定不垂直。
D
检测目标
一个长方体如图,和AA′平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。
A′
B′
C′
D′
和AA′平行的棱有3条:
BB′∥AA′,CC′∥AA′,DD′∥AA′。
和AB平行的棱有3条:
A′B′∥AB,C′D′∥AB,CD∥AB。
检测目标
下列说法正确的是(
)
A、在同一平面内,不相交的两条射线是平行线;
B、在同一平面内,不相交的两条线段是平行线;
C、在同一平面内,两条直线的位置关系不相交就平行;
D、不相交的两条直线是平行线
C
检测目标
下列语句中,正确的个数是(
)?
(1)不相交的两条直线是平行线
(2)同一平面内,两直线的位置关系有两种,即相交或平行
(3)若线段AB与CD没有交点则AB//CD
(4)若a//b,b//c,则a与c不相交
(A)1个
(B)2个
(C)3个
(D)4个
检测目标
C
·
A
·
B
(3)经过点C能画出几条直线与直线AB平行?
(4)过点D画一条直线与直线AB平行,与(3)中所画的直线平行吗?
·
·
C
D
(1)经过点C能画出几条直线?
无数条
1条
a
b
(2)与直线AB平行的直线有几条?
无数条
平行
你能对这些情况进行归纳总结吗?
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
温故知新
1.什么是同位角?有何特征?
2.什么是同旁内角?有何特征?
3.什么是内错角?有何特征?
角的
名称
角的特征
基本图形
基本图形
相同点
共同特征
同位角
同旁
内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
温故知新
导入新课
我们学习了“三线八角”,侧重从角的角度探究;那么,两条直线的位置关系,又有哪几种情况呢?
5.2.1
平
行
线
人教版七年级数学
下册
学习目标:
1.了解平行线的概念,知道同一平面内不重合的两条直线的两种位置关系,
能叙述平行公理以及平行公理的推论.
2.会用符号语言表示平行公理及其推论,
会用三角尺和直尺过已知直线外一点画这条直线的平行线.
学习重、难点:
重点:平行公理及其推论.
难点:文字语言、图形语言、符号语言的
相互转换.
生活中的平行线
如图,直线
a、b
是铁路上的两条铁轨,它们会相交吗?今天我们就来研究这样的两条直线——平行线.
a
b
思考:如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
a
b
c
a
b
c
a
b
c
目标导学一:平行线的定义及表示
同一平面内两直线的位置关系:
平行
相交
垂直
相交但不垂直
a
b
a⊥b
a
∥b
a
b
b
a
在木条转动过程中,存在一条直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作“a∥b”.
在同一平面内,不相交的两条直线叫做平行线.
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是“两条直线”而不是两条射线或两条线段.
平行线的概念
a
b
c
正方体这两条边所在的直线,既不相交,也不平行
平行的概念
平行线的理解
【问题1】在同一平面内,两条不重合的直线有几种位置关系呢?
【问题2】不相交的两条直线一定是平行吗?
相交
平行
不一定
在同一平面内,两直线的位置关系有平行与相交两种。
A
D
B
C
a
b
记作:AB∥CD
读作:直线AB平行于直线CD
记作:a∥b
读作:直线a平行于直线b
一般,我们用“∥”这个符号表示平行
平行线的几何语言:
例:观察如图所示的长方体后填空:
(1)用符号表示下列两棱的位置关系:
A1B1
AB,
AA1
AB,
A1D1
C1D1,
AD
BC。
(2)
A1B1与BC所在的直线是两条不
相交的直线,他们
平行。
(填“是”或“不是”),
由此可知,在
内,两条
不相交的直线才能叫做平行线。
∥
∥
⊥
⊥
同一平面
C
B
D
B1
A1
A
C1
D1
不是
你能举出一些平行线的例子吗?
黑
板
跑道
游泳池
各国国旗
俄罗斯
马来西亚
泰国
探究与思考
给一条直线a,你能画出直线a的平行线吗?
a
b
平行线的画法
:一放、二靠、三推、四画。
目标导学二:平行线的画法、平行公理及其推论
探究与思考
过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?
a
B
C
b
c
探究与思考
尺子的摆放只有这一种吗,换一种方法过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?
a
B
C
b
c
请按图所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法中,三角板起着什么作用?
(2)
把图中的直线
,
看成被尺边AB所截,那么在画图过程中,什么角始终保持相等?由此你能发现画两直线平行方法的依据吗?
想一想!
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践
平行公理:经过直线外一点,有且只有一条直线与已知
直线平行.
·
A
·
B
·
·
C
D
a
b
由以上的实践你发现了什么?
说说看
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
平行公理
经过直线外一点,有且只有一条直线与这条直线平行.?
a
b
直线上就不行
存在且唯一
如图:三条直线a、b、c。如果a//c,b//c,
那么直线a与b有什么关系?
F
E
b
a
假设a与b相交,
设a与b相交于O
因为a//c,b//c
于是过点O就有两条直线a,b都与c平行。
根据平行公理,这是不可能的
也就是说,a与b不能相交,
只能平行。
O
c
平行公理的推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
平行线具有传递性.
b
a
c
因为
b∥a,c
∥a,
所以
b∥c.
几何语言表达:
c
b
a
平行公理的推论(平行线的传递性):
∵a//c
,
c//b(已知)
?
a//b(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
平行线的两条性质:
平面内,经过直线外一点,有且只有一条直线与这条直线平行.
①平行公理:
(唯一性)
②推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
(平行线的传递性)
如果b∥a,
c∥a,
那么b∥c.
例:完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB
//
DE,BC
//
DE(已知)。所以
A,B,C三点___________(
)
(2)如图2所示,因为AB
//
CD,CD
//
EF(已知),所以
________
//
_________(
)
·
·
·
A
D
E
B
C
图
1
A
B
C
D
E
F
图
2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
如图,直线a
∥b,b∥c,c∥d,那么a
∥d吗?为什么?
a
b
c
d
解:
因为
a
∥b,b∥c,
所以
a
∥c
(
)
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为
c∥d,
所以
a
∥d
(
)
能力拓展
平行线
平行线的定义和画法
平行公理及其推导
定义
画法
平行公理
推论
一落;二靠;三移;四画
a
P
b
c
如果b∥a,c∥a,那么b∥c.
课堂小结
判断下列说法是否正确,并说明理由.?
不相交的两条直线是平行线.
在同一平面内,两条不相交的线段是平行线.
过一点可以而且只可以画一条直线与已知直线平行.
(
)
(
)
(
)
检测目标
①
过两点有且只有一条直线.
②
两条不同的直线有且只有一个公共点.
③
过一点有且只有一条直线与己知直线垂直。
④
过一点有且只有一条直线与己知直线平行。
(A)1
(B)
2
(C)3 (D)4
在同一平面内,下列说法中,正确的有(
)个.
√
×
√
×
B
检测目标
下列推理正确的是(
)
A、因为a
//
d,b
//
c,所以c
//
d;
B、因为a
//
c,b
//
d,所以c
//
d;
C、因为a
//
b,a
//
c,所以b
//
c;
D、因为a
//
b,c
//
d,所以a
//
c。
C
检测目标
下列说法中正确的是(
)
A.两条相交的直线叫做平行线
B.如果a∥b,b∥c,则a不与c平行
C.在直线外一点,只能画出一条直线与已知直线平行
D.两条不平行的射线,在同一平面内一定相交
【详解】
A.在同一平面内,不相交的两条直线叫平行线,故本选项错误;
B.如果a∥b,b∥c,则a与c平行,故本选项错误;
C.在直线外一点,只能画出一条直线与已知直线平行,故本选项正确;
D.两条不平行的射线,在同一平面内不一定相交,故本选项错误;故选:C.
检测目标
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行
下列说法正确的是(
)
检测目标
在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A.1cm
B.3cm
C.5cm或3cm
D.1cm或3cm
【答案】C
【解析】详解:当直线c在a、b之间时,
∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4-1=3(cm);
当直线c不在a、b之间时,
∵a、b、c是三条平行直线,而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4+1=5(cm),
综上所述,a与c的距离为3cm或5cm.故选:C.
检测目标
下列说法正确的是(
)
A、在同一平面内,两条直线的位置关系有相交,垂直,平行三种。
B、在同一平面内,不垂直的两直线必平行。
C、在同一平面内,不平行的两直线必垂直。
D、在同一平面内,不相交的两直线一定不垂直。
D
检测目标
一个长方体如图,和AA′平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。
A′
B′
C′
D′
和AA′平行的棱有3条:
BB′∥AA′,CC′∥AA′,DD′∥AA′。
和AB平行的棱有3条:
A′B′∥AB,C′D′∥AB,CD∥AB。
检测目标
下列说法正确的是(
)
A、在同一平面内,不相交的两条射线是平行线;
B、在同一平面内,不相交的两条线段是平行线;
C、在同一平面内,两条直线的位置关系不相交就平行;
D、不相交的两条直线是平行线
C
检测目标
下列语句中,正确的个数是(
)?
(1)不相交的两条直线是平行线
(2)同一平面内,两直线的位置关系有两种,即相交或平行
(3)若线段AB与CD没有交点则AB//CD
(4)若a//b,b//c,则a与c不相交
(A)1个
(B)2个
(C)3个
(D)4个
检测目标
C
·
A
·
B
(3)经过点C能画出几条直线与直线AB平行?
(4)过点D画一条直线与直线AB平行,与(3)中所画的直线平行吗?
·
·
C
D
(1)经过点C能画出几条直线?
无数条
1条
a
b
(2)与直线AB平行的直线有几条?
无数条
平行
你能对这些情况进行归纳总结吗?
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
