人教版七年级数学 下册 第五章 5.2.2 平行线的判定 课件(共49张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第五章 5.2.2 平行线的判定 课件(共49张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览








文档简介
(共49张PPT)
温故知新
1.两条不重合的直线有哪几种位置关系?
2.什么是平行线?
3.平行公理及逆定理分别是什么?
根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行。如何证明两条直线平行呢?今天我们就来探究平行线的判定。
导入新课
5.2.2
平行线的判定
人教版七年级数学
下册
目标导航
1.掌握平行线的三种判定方法,会运用判定方法来判断两条直线是否平行;
2.能够根据平行线的判定方法进行简单的推理。
3.掌握垂直于同一条直线的两条直线互相平行。
●
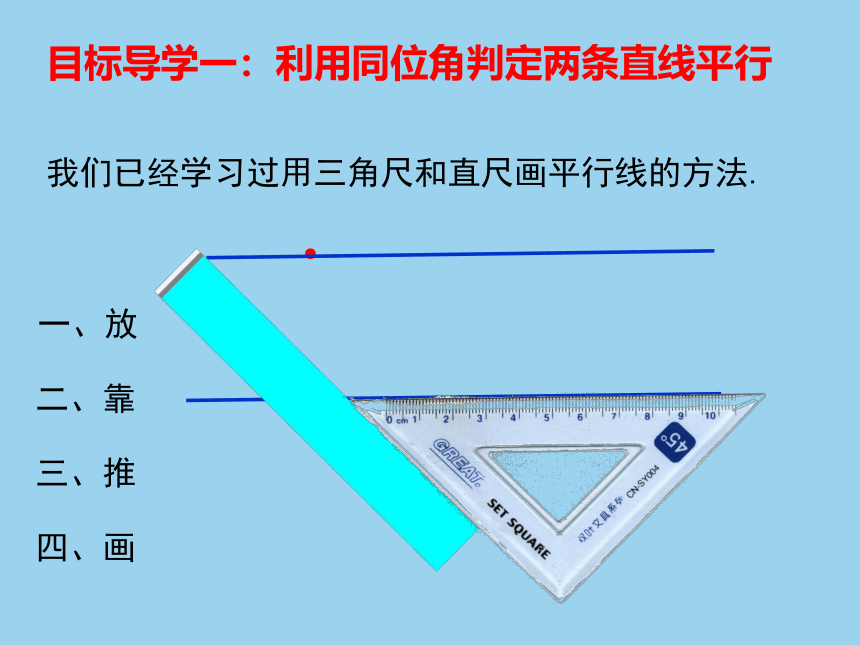
一、放
二、靠
三、推
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
目标导学一:利用同位角判定两条直线平行
b
A
2
1
a
B
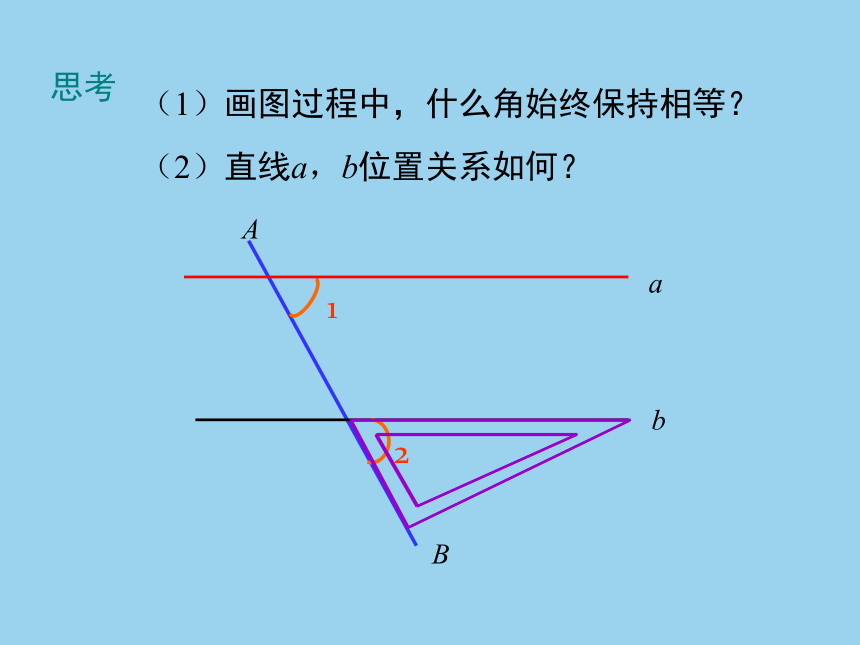
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
思考
(3)将其最初和最终的两种特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(4)
由上面的操作过程,你能发现判定两直线平行的方法吗?
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1=∠2(已知)
∴l1∥l2
(同位角相等,两直线平行)
1
2
l2
l1
A
B
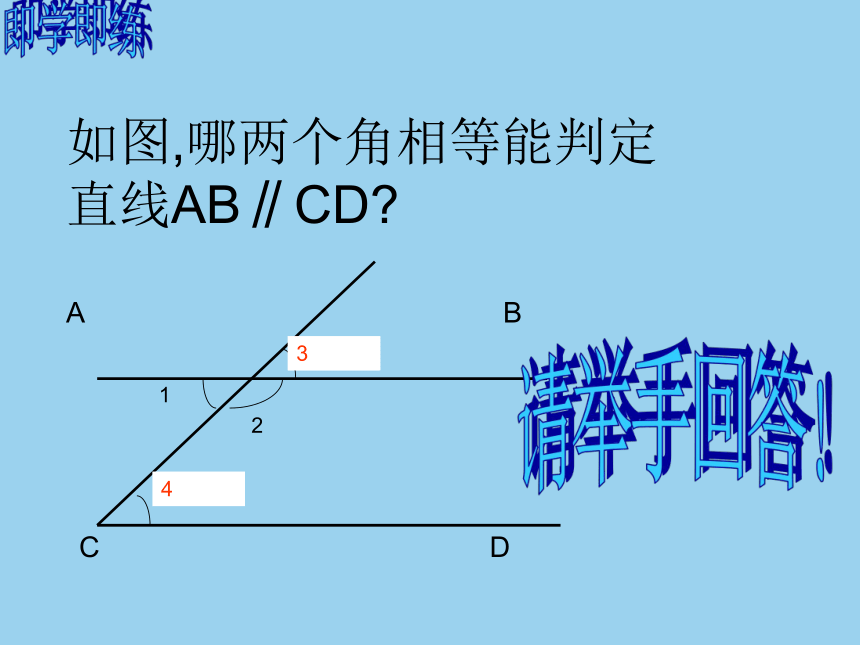
如图,哪两个角相等能判定直线AB∥CD?
1
4
3
2
A
D
C
B
请举手回答!
4
3
即学即练
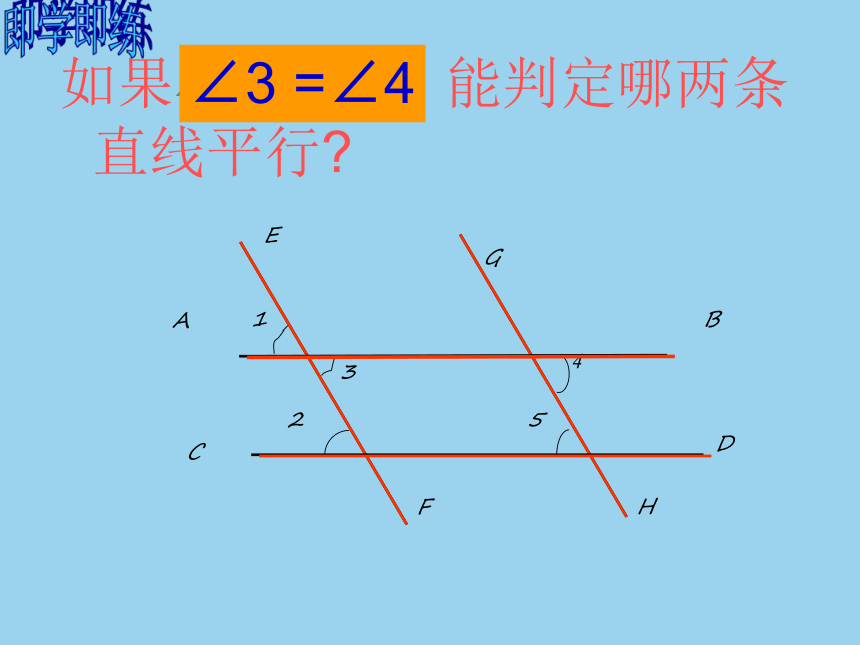
如果
,
能判定哪两条直线平行?
∠1
=∠2
4
1
2
3
A
B
C
E
F
D
5
H
G
∠3
=∠4
即学即练
如图,哪两个角相等能判定直线AB∥CD?
B
1
4
3
2
A
C
答案:∠3和∠4(同位角相等,两直线平行)
即学即练
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
目标导学二:利用内错角、同旁内角判定两条直线平行
先看内错角,如果∠2=∠3,能得出a∥b吗?
因为∠2=∠3(已知),
∠3=∠1(对顶角相等)
所以∠1=∠2(等量代换)
所以a∥b(同位角相等,两直线平行)
内错角相等,两直线平行
判定方法2
简单说成:
两条直线被第三条直线所截,
如果内错角相等,
那么这两条直线平行.
内错角相等,两直线平行.
例:如图,已知BC平分∠ACD,且∠1=∠2,AB与CD平行吗?为什么?
解:AB∥CD.理由如下:
∵BC平分∠ACD,
∴∠1=∠BCD.
∵∠1=∠2,
∴∠2=∠BCD,
∴AB∥CD(内错角相等,两直线平行).
如图,∠1=
∠2
,且∠1=∠3,
AB和CD平行吗?
A
B
C
D
1
2
3
解:
∵∠1=∠2,∠1=∠3
∴∠2=∠3
∴AB∥CD
即学即练
a
b
c
1
2
A
B
3
解:∵
∠1+∠3
=180°,
∠2+∠3
=180°
∴
∠2=∠1(同角的补角相等)
∴
a∥b(同位角相等,两直线平行)
如图,已知∠1+∠3=180°,
试说明a∥b.
再看同旁角,如果∠1+∠3=180°,能得出a∥b吗?
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?(利用内错角知识证明)
a
b
c
1
2
A
B
3
解:∵
∠1+∠3
=180°,
∠2+∠3
=180°
∴
∠2=∠1(同角的补角相等)
∴
a∥b(同旁内角互补,两直线平行)
如图,已知∠1+∠3=180°,
试说明a∥b.
平行线判定方法3
两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行
简写为:同旁内角互补,两直线平行
几何描述:
∵
∠1+∠2=180°(已知)
∴
a∥b(同旁内角互补,两直线平行)
a
b
c
1
A
B
2
D
C
B
A
答:AB//CD,AD//BC
∵?
B=45°(已知)
?
C=135°(已知)
??
B+
?
C=180°
?
AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
如图:?B=
?
D=45°,
?
C=135°,问图中有哪些直线平行?
即学即练
文字叙述
符号语言
图形
相等,
两直线平行
∵
(已知),
∴a∥b
相等,
两直线平行
∵
(已知),
∴a∥b
互补,
两直线平行
∵
(已知)
∴a∥b
判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
方法小结
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
直线平行的条件:
直线平行的条件:
寻找
同位角相等
内错角相等
同旁内角互补
目标导学三:平行线的判定的综合运用
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?
为什么?
例:
如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?
为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行?
为什么?
A
B
D
C
E
F
G
解
(1)AB//CD,
同位角相等,两直线平行;
(2)AD//BC,
内错角相等,两直线平行;
(3)AD//EF,
同旁内角互补,两直线平行.
例:如图:
∠C+∠A=
∠
AEC,判断AB与CD是否平行,并说明理由;
A
B
C
D
E
F
分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。
1.如图所示,由∠DCE
=
∠
D,可判断哪两条直线平行?由∠1=
∠
2,可判断哪两条直线平行?
2.如图,已知
∠A与∠
D互补,
可判断哪两条直线平行?
∠B与哪个角互补,可判断AD平行BC?
B
AD//BE
AB//DC
AB//DC
∠A
即学即练
例:如图,当∠1=∠2时,AB
与CD平行吗?为什么?
答:
AB∥CD
.
理由如下:
∵
∠1=∠2,
又∵
∠2=∠3
,
∴
∠1=∠3
.
∵
∠1和∠3是同位角
,
∴
AB∥CD(同位角相等,两直线平行).
平行线判定的实际应用
我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图,是光线从空气中射入水中,再从水中射入空气中的示意图.由于折射率相同,因此已知∠1=∠4,∠2=∠3,请你用所学知识来判断
c
与d?是否平行?并说明理由.
探究:在同一平面内,两条直线垂直于同一条直线,
这两条直线平行吗?为什么?
a
b
c
b⊥a,c⊥a
b∥c
?
猜想:垂直于同一条直线的两条直线平行.
目标导学四:在同一平面内,垂直于同一条直线的两条直线平行
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
a
b
c
1
2
∵b⊥a
,c
⊥a
(已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1=
∠2
=
90°
(垂直的定义)
解法1:如图,
探究:
∵
b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
探究:
∵
b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴
∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
解法3:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
探究:
同一平面内,垂直于同一条直线
的两条直线平行.
几何语言:
∵
b⊥a,c⊥a(已知)
∴b∥c(同一平面内,垂直于同一条直线的两条
直线平行.)
a
b
c
1
2
补充:有一块长方形的玻璃,你能用什么方法检查它的对边是平行的?
解:可以通过测量玻璃的四个角,看相邻两个角的和是否为180°,若是,就平行.
小结:想一想,你有多少种判定直线平行的方法?
1.同位角相等
2.内错角相等
3.同旁内角互补
两直线平行
平行条件
条件:
角的关系
平行关系
4.
平行于同一直线的两直线平行
5.在同一平面内,垂直于同一条直线的两直线平行
6.平行线的定义.
课堂小结
下面几种说法中,正确的是( )
A.同一平面内不相交的两条线段平行
B.同一平面内不相交的两条射线平行
C.同一平面内不相交的两条直线平行
D.以上三种说法都不正确
C
检测目标
如图,下列条件中,能判断AB∥CD的是(
A
)
A.∠C+∠CEB=180°
B.∠BFC+∠C=180°
C.∠AEC=∠EFC
D.∠AEC=∠EFD
检测目标
平面上五条直线l1,l2,l3,l4和l5相交的情形如图所示,根据图中标出的角度,下列叙述正确的是(
A
)
A.l1和l3不平行,l2和l3平行
B.l1和l3不平行,l2和l3不平行
C.l1和l3平行,l2和l3平行
D.l1和l3平行,l2和l3不平行
检测目标
在下面的四个图形中,已知∠1=∠2,那么能判定AB∥CD的是(
A
)
检测目标
如图,已知∠ABC=∠BCD,∠ABC+∠CDG=180°,求证:BC∥GD.
检测目标
证明:∵∠ABC=∠BCD,∠ABC+∠CDG=180°,
∴∠BCD+∠CDG=180°,
∴BC∥GD(
同旁内角互补,两直线平行
).
?
如图,由∠D+∠A=
180°可以判定哪两条直线平行?根据是什么?
∠A和∠D是AB和CD被AD所截形成的同旁内角,
所以AB∥CD,依据是同旁内角互补,两直线平行.
检测目标
在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么?
解:①通过度量∠3的度数,
若满足∠2+∠3=180°,
根据同旁内角互补,两直线平行,
就可以验证这个结论;
②通过度量∠4的度数,若满足∠2=∠4,
根据同位角相等,两直线平行,就可以验证这个结论;
③通过度量∠5的度数,若满足∠2=∠5,
根据内错角相等,两直线平行,就可以验证这个结论.
检测目标
已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?
平行线判定综合
答:
AB∥CD
.
理由如下:
∵
AC平分∠BAD,∴
∠1=∠3
.
∵∠1=∠2,∴
∠2=∠3
.
∵
∠2和∠3是内错角,
∴
AB∥CD(内错角相等,两直线平行).
检测目标
如图,已知CD⊥DA,AB⊥AD,∠1=∠2,问DF与AE平行吗?
检测目标
(变式):如图,已知AB,CD被EF所截,∠1=∠2,∠CNF=∠BME,
试说明①AB∥CD
;②MP∥NQ
1
2
B
D
A
C
E
F
M
N
P
Q
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
温故知新
1.两条不重合的直线有哪几种位置关系?
2.什么是平行线?
3.平行公理及逆定理分别是什么?
根据平行线的定义,如果同一平面内的两条直线不相交,就可以判断这两条直线平行。如何证明两条直线平行呢?今天我们就来探究平行线的判定。
导入新课
5.2.2
平行线的判定
人教版七年级数学
下册
目标导航
1.掌握平行线的三种判定方法,会运用判定方法来判断两条直线是否平行;
2.能够根据平行线的判定方法进行简单的推理。
3.掌握垂直于同一条直线的两条直线互相平行。
●
一、放
二、靠
三、推
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
目标导学一:利用同位角判定两条直线平行
b
A
2
1
a
B
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
思考
(3)将其最初和最终的两种特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(4)
由上面的操作过程,你能发现判定两直线平行的方法吗?
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1=∠2(已知)
∴l1∥l2
(同位角相等,两直线平行)
1
2
l2
l1
A
B
如图,哪两个角相等能判定直线AB∥CD?
1
4
3
2
A
D
C
B
请举手回答!
4
3
即学即练
如果
,
能判定哪两条直线平行?
∠1
=∠2
4
1
2
3
A
B
C
E
F
D
5
H
G
∠3
=∠4
即学即练
如图,哪两个角相等能判定直线AB∥CD?
B
1
4
3
2
A
C
答案:∠3和∠4(同位角相等,两直线平行)
即学即练
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
目标导学二:利用内错角、同旁内角判定两条直线平行
先看内错角,如果∠2=∠3,能得出a∥b吗?
因为∠2=∠3(已知),
∠3=∠1(对顶角相等)
所以∠1=∠2(等量代换)
所以a∥b(同位角相等,两直线平行)
内错角相等,两直线平行
判定方法2
简单说成:
两条直线被第三条直线所截,
如果内错角相等,
那么这两条直线平行.
内错角相等,两直线平行.
例:如图,已知BC平分∠ACD,且∠1=∠2,AB与CD平行吗?为什么?
解:AB∥CD.理由如下:
∵BC平分∠ACD,
∴∠1=∠BCD.
∵∠1=∠2,
∴∠2=∠BCD,
∴AB∥CD(内错角相等,两直线平行).
如图,∠1=
∠2
,且∠1=∠3,
AB和CD平行吗?
A
B
C
D
1
2
3
解:
∵∠1=∠2,∠1=∠3
∴∠2=∠3
∴AB∥CD
即学即练
a
b
c
1
2
A
B
3
解:∵
∠1+∠3
=180°,
∠2+∠3
=180°
∴
∠2=∠1(同角的补角相等)
∴
a∥b(同位角相等,两直线平行)
如图,已知∠1+∠3=180°,
试说明a∥b.
再看同旁角,如果∠1+∠3=180°,能得出a∥b吗?
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?(利用内错角知识证明)
a
b
c
1
2
A
B
3
解:∵
∠1+∠3
=180°,
∠2+∠3
=180°
∴
∠2=∠1(同角的补角相等)
∴
a∥b(同旁内角互补,两直线平行)
如图,已知∠1+∠3=180°,
试说明a∥b.
平行线判定方法3
两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行
简写为:同旁内角互补,两直线平行
几何描述:
∵
∠1+∠2=180°(已知)
∴
a∥b(同旁内角互补,两直线平行)
a
b
c
1
A
B
2
D
C
B
A
答:AB//CD,AD//BC
∵?
B=45°(已知)
?
C=135°(已知)
??
B+
?
C=180°
?
AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
如图:?B=
?
D=45°,
?
C=135°,问图中有哪些直线平行?
即学即练
文字叙述
符号语言
图形
相等,
两直线平行
∵
(已知),
∴a∥b
相等,
两直线平行
∵
(已知),
∴a∥b
互补,
两直线平行
∵
(已知)
∴a∥b
判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
方法小结
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
直线平行的条件:
直线平行的条件:
寻找
同位角相等
内错角相等
同旁内角互补
目标导学三:平行线的判定的综合运用
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?
为什么?
例:
如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?
为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行?
为什么?
A
B
D
C
E
F
G
解
(1)AB//CD,
同位角相等,两直线平行;
(2)AD//BC,
内错角相等,两直线平行;
(3)AD//EF,
同旁内角互补,两直线平行.
例:如图:
∠C+∠A=
∠
AEC,判断AB与CD是否平行,并说明理由;
A
B
C
D
E
F
分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。
1.如图所示,由∠DCE
=
∠
D,可判断哪两条直线平行?由∠1=
∠
2,可判断哪两条直线平行?
2.如图,已知
∠A与∠
D互补,
可判断哪两条直线平行?
∠B与哪个角互补,可判断AD平行BC?
B
AD//BE
AB//DC
AB//DC
∠A
即学即练
例:如图,当∠1=∠2时,AB
与CD平行吗?为什么?
答:
AB∥CD
.
理由如下:
∵
∠1=∠2,
又∵
∠2=∠3
,
∴
∠1=∠3
.
∵
∠1和∠3是同位角
,
∴
AB∥CD(同位角相等,两直线平行).
平行线判定的实际应用
我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图,是光线从空气中射入水中,再从水中射入空气中的示意图.由于折射率相同,因此已知∠1=∠4,∠2=∠3,请你用所学知识来判断
c
与d?是否平行?并说明理由.
探究:在同一平面内,两条直线垂直于同一条直线,
这两条直线平行吗?为什么?
a
b
c
b⊥a,c⊥a
b∥c
?
猜想:垂直于同一条直线的两条直线平行.
目标导学四:在同一平面内,垂直于同一条直线的两条直线平行
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
a
b
c
1
2
∵b⊥a
,c
⊥a
(已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1=
∠2
=
90°
(垂直的定义)
解法1:如图,
探究:
∵
b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(内错角相等,两直线平行)
a
b
c
1
2
解法2:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
探究:
∵
b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴
∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
a
b
c
1
2
解法3:如图,
在同一平面内,b⊥a,c⊥a,试说明:b∥c.
探究:
同一平面内,垂直于同一条直线
的两条直线平行.
几何语言:
∵
b⊥a,c⊥a(已知)
∴b∥c(同一平面内,垂直于同一条直线的两条
直线平行.)
a
b
c
1
2
补充:有一块长方形的玻璃,你能用什么方法检查它的对边是平行的?
解:可以通过测量玻璃的四个角,看相邻两个角的和是否为180°,若是,就平行.
小结:想一想,你有多少种判定直线平行的方法?
1.同位角相等
2.内错角相等
3.同旁内角互补
两直线平行
平行条件
条件:
角的关系
平行关系
4.
平行于同一直线的两直线平行
5.在同一平面内,垂直于同一条直线的两直线平行
6.平行线的定义.
课堂小结
下面几种说法中,正确的是( )
A.同一平面内不相交的两条线段平行
B.同一平面内不相交的两条射线平行
C.同一平面内不相交的两条直线平行
D.以上三种说法都不正确
C
检测目标
如图,下列条件中,能判断AB∥CD的是(
A
)
A.∠C+∠CEB=180°
B.∠BFC+∠C=180°
C.∠AEC=∠EFC
D.∠AEC=∠EFD
检测目标
平面上五条直线l1,l2,l3,l4和l5相交的情形如图所示,根据图中标出的角度,下列叙述正确的是(
A
)
A.l1和l3不平行,l2和l3平行
B.l1和l3不平行,l2和l3不平行
C.l1和l3平行,l2和l3平行
D.l1和l3平行,l2和l3不平行
检测目标
在下面的四个图形中,已知∠1=∠2,那么能判定AB∥CD的是(
A
)
检测目标
如图,已知∠ABC=∠BCD,∠ABC+∠CDG=180°,求证:BC∥GD.
检测目标
证明:∵∠ABC=∠BCD,∠ABC+∠CDG=180°,
∴∠BCD+∠CDG=180°,
∴BC∥GD(
同旁内角互补,两直线平行
).
?
如图,由∠D+∠A=
180°可以判定哪两条直线平行?根据是什么?
∠A和∠D是AB和CD被AD所截形成的同旁内角,
所以AB∥CD,依据是同旁内角互补,两直线平行.
检测目标
在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么?
解:①通过度量∠3的度数,
若满足∠2+∠3=180°,
根据同旁内角互补,两直线平行,
就可以验证这个结论;
②通过度量∠4的度数,若满足∠2=∠4,
根据同位角相等,两直线平行,就可以验证这个结论;
③通过度量∠5的度数,若满足∠2=∠5,
根据内错角相等,两直线平行,就可以验证这个结论.
检测目标
已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?
平行线判定综合
答:
AB∥CD
.
理由如下:
∵
AC平分∠BAD,∴
∠1=∠3
.
∵∠1=∠2,∴
∠2=∠3
.
∵
∠2和∠3是内错角,
∴
AB∥CD(内错角相等,两直线平行).
检测目标
如图,已知CD⊥DA,AB⊥AD,∠1=∠2,问DF与AE平行吗?
检测目标
(变式):如图,已知AB,CD被EF所截,∠1=∠2,∠CNF=∠BME,
试说明①AB∥CD
;②MP∥NQ
1
2
B
D
A
C
E
F
M
N
P
Q
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
