人教版七年级数学 下册 第五章 5.3.1 平行线的性质 课件(共54张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第五章 5.3.1 平行线的性质 课件(共54张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览






文档简介
(共54张PPT)
温故知新
1.什么是平行线?
2.平行线的判定方法有哪些?
平行线的判定方法
同位角相等,
两直线平行。
内错角相等,
两直线平行。
同旁内角互补,
两直线平行。
这些判定方法先知道什么,后知道什么?
如果两条直线平行,那么这两条平行线被第三条直线所截而成的8个角会有什么关系呢?
5.3.1
平行线的性质
人教版七年级数学
下册
目标导航
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补。
2.能够根据平行线的性质进行简单的推理。
3.运用平行线的性质和判定进行简单的推理和计算。
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
思考
通过上题可知平行线的判定方法是什么?
探究
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
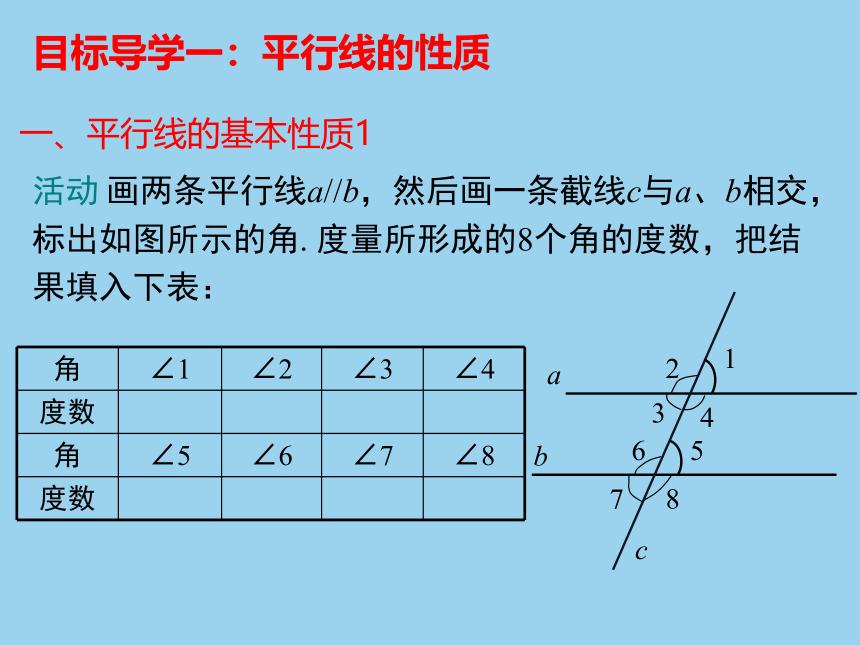
活动
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角.
度量所形成的8个角的度数,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
b
1
2
a
c
5
6
7
8
3
4
一、平行线的基本性质1
目标导学一:平行线的性质
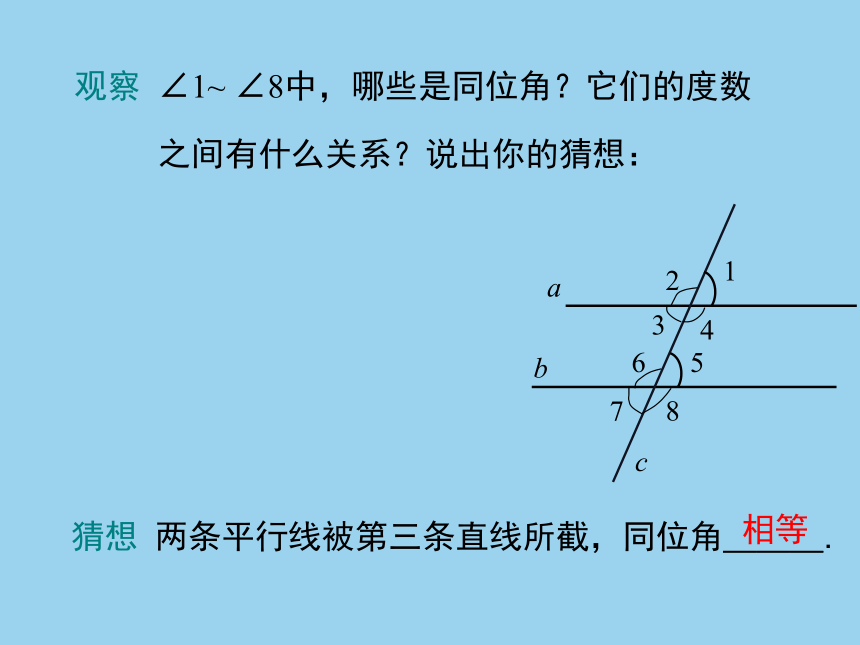
观察
∠1~
∠8中,哪些是同位角?它们的度数
之间有什么关系?说出你的猜想:
猜想
两条平行线被第三条直线所截,同位角___.
相等
b
1
2
a
c
5
6
7
8
3
4
a
b
d
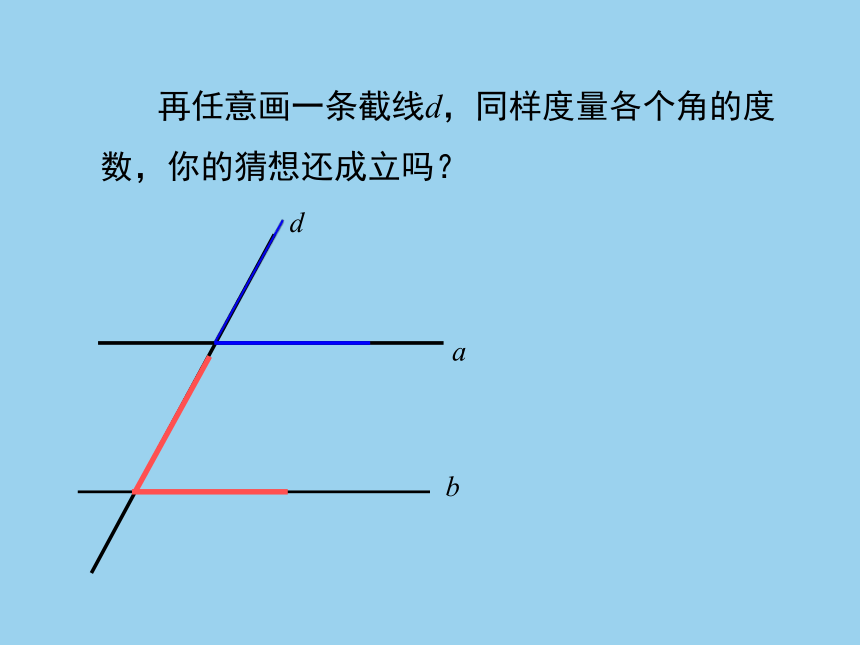
再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?
如果两直线不平行,上述结论还成立吗?
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
归纳
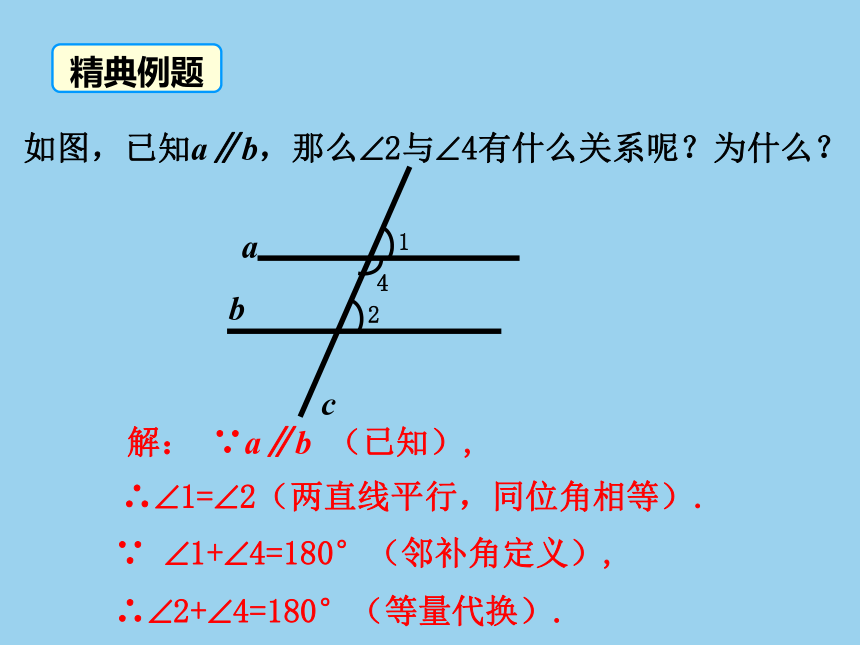
如图,已知a∥b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
解:
∵a∥b
(已知),
∴?1=?2(两直线平行,同位角相等).
∵
?1+?4=180°(邻补角定义),
∴?2+?4=180°(等量代换).
精典例题
思考:在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等,
能否得到内错角之间的数量关系?
二、平行线的基本性质2
如图:已知a//b,那么?2与?3相等吗?
为什么?
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵
∠1=∠3(对顶角相等),
∴
∠2=∠3(等量代换).
b
1
2
a
c
3
思考
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
∴∠ABD=∠BDC(两直线平行,内错角相等)
证明:∵AB∥CD(已知)
∵AE∥BD(
已知)
∴∠BDC=∠E
(两直线平行,同位角相等)
∴∠ABD=∠E(等量代换)
如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
精典例题
如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?
B
C
即学即练
如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?
B
C
答:∠C=142o
即学即练
如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?
B
C
答:∠C=142o
因为拐弯前后的两条路互相平行,∠B和∠C是两条平行线的内错角,根据两直线平行,内错角相等,∠C=∠B=142o
即学即练
如图,已知a//b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
解:
∵a//b
(已知),
∴?
1=
?
2
(两直线平行,同位角相等).
∵
?
1+
?
4=180°
(邻补角的性质),
∴?
2+
?
4=180°
(等量代换).
思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
三、平行线的基本性质3
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
∴?
2+
?
4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
例:如图,梯形ABCD中,AB//CD,∠D=(
)
A.
120°
B.
135°
C.
145°
D.
155°
B
精典例题
例:如图,
AB//CD,AD//BC.
求证:∠A=∠C.
证明:∵AB//CD(已知),
∴∠A+∠D=180°(两直线平行,同旁内角互补).
∵AD//BC(已知),
∴∠C+∠D=180°(两直线平行,同旁内角互补).
∴∠A=∠C(同角的补角相等).
即学即练
图形
已知
结果
结论
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
2
∠1=
∠2
∠3=
∠2
∠4+
∠2=1800
知识归纳
你能区别平行线的判定与性质吗?
四、平行线的判定与性质
同位角相等
内错角相等
同旁内角互补
两直线平行。
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
性质
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
性质
平行线的判定是先知道角相等或互补,后知道两直线平行。
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
性质
平行线的判定是先知道角相等或互补,后知道两直线平行。
平行线的性质是先知道两直线平行,后知道角相等或互补。
你能区别平行线的判定与性质吗?
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的性质与判断的关系
例:如图,已知平行线AB、CD被直线AE所截
(1)从
∠1=110o可以知道∠2
是多少度吗,为什么?
(2)从∠1=110o可以知道
∠3是多少度吗,为什么?
(3)从
∠1=110o可以知道∠4
是多少度吗,为什么?
2
3
E
1
4
A
B
D
C
解:(1)∠2=110o
∵两直线平行,内错角相等;
(2)∠3=110o
∵两直线平行,
同位角相等;
(3)∠4=70o
∵两直线平行,同旁内角互补.
精典例题
例:如图,一条公路两次拐弯的前后两条路互相平行。第
一次拐弯时∠B是142°,第二次拐弯时∠C是多少度?
为什么?
解:∠C=142o
∵两直线平行,内错角相等.
B
C
精典例题
思维拓展:如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3,
∵两直线行,内错角相等;
∵∠1=∠2=∠3=∠4,
∴
∠5=∠6,
∴进入潜望镜的光线和
离开潜望镜的光线平行.
例1:如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B
=
60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
C
解:(1)
DE∥BC.理由如下:
∵
∠ADE=60°,∠B
=
60°
∴
∠ADE=∠B
∴
DE∥BC
(同位角相等,两直线平行
).
A
B
D
E
目标导学二:平行线的性质和判定及其综合应用
例:如下图一块梯形贴片的残余部分,量的∠A=100°,∠B=115°,另外两个角分别是多少度?
A
B
C
D
解:∵该四边形ABCD是梯形
∴AB∥CD
∴∠A+∠D=180°
∠B+∠C=180°(两直线平行,同旁内角互补)
∴
∠D=180°-
∠A
=
180°-
100°=80°
∠C=180°-
∠B
=
180°-
115°=65°
所以梯形的另外两个角分别是80°、65°
例:如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,
梯形另外两个角分别是多少度?
①梯形这个条件说明
∥
.
②∠A与∠D、∠B
与∠C的位置关系是
,
数量关系是
.
③所以∠D=
,∠C=
.
同旁内角
互补
80°
65°
DC
AB
已知:AB∥CD,∠1
=
∠2.试说明:BE∥CF.
证明:
∵AB
∥
CD
∴∠ABC=∠BCD
(两直线平行,内错角相等)
∵∠1=∠2
∴∠ABC
-∠1=∠BCD-
∠2
即∠3=∠4
∴
BE∥CF
(内错角相等,两直线平行)
即学既练
1
它与地面所
成的较大的
角是多少度
95
0
目前,它与地面所成的较小的角
为∠1=85?
2
3
联系生活
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
课堂小结
判定:已知角的关系得平行的关系.
推平行,用判定.
性质:已知平行的关系得角的关系.
知平行,用性质.
平行线的“判定”与“性质”有什么不同:
课堂小结
1.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14°
B.15°
C.16°
D.17°
C
检测目标
2.
如图,直线a//b,直线c与直线a,b相交,
若∠1=56°,则∠2等于(
)
A.
24°
B.
34°
C.
56°
D.
124°
C
检测目标
3.如图,∠BCD=95°,AB∥DE,则∠α与∠β满足(
)
A.∠α+∠β=95°
B.∠β﹣∠α=95°
C.∠α+∠β=85°
D.∠β﹣∠α=85°
【答案】D
【详解】
解:过点C作CF∥AB
∵AB∥DE,CF∥AB∴AB∥DE∥CF
∴∠BCF=∠α,∠DCF+∠β=180°
∴∠BCD=∠BCF
+∠DCF
∴∠α+180°-∠β=95°
∴∠β﹣∠α=85°故选:D
检测目标
4.如图,AB∥CD,则,,则的大小是(
)
A.
B.
C.
D.
【答案】B
【详解】
∵∠DEC=100°,∠C=40°,
∴∠D=180°-∠DEC-∠C=40°,
又∵AB∥CD,
∴∠B=∠D=40°,
故选B.
检测目标
5.如图,已知直线a,b被直线c所截,在括号内为下面各小题推理填上适当的根据:
(1)∵
a∥b,
∴∠1=∠3(
).
a
b
c
1
2
3
4
两直线平行,同位角相等
(2)∵
∠1=
∠3,
∴a∥b(
).
同位角相等,两直线平行
(3)∵a∥b
,
∴∠1=∠2(
).
两直线平行,内错角相等
检测目标
6.如图,BCD是一条直线,∠A=75°,
∠1=53°,∠2=75°,求∠B的度数.
B
A
C
D
E
1
2
解:
∵∠A=∠2=75°,
∴AB∥CE,
∴∠B=∠1=53°.
检测目标
7.已知:AB∥CD,∠1
=
∠2.试说明:BE∥CF.
证明:
∵AB
∥
CD(已知)
∴∠ABC=∠BCD
(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠ABC
-∠1=∠BCD-
∠2(等式性质)
即∠3=∠4
∴
BE∥CF(内错角相等,两直线平行)
1
2
4
3
检测目标
8.如图,直线a∥b,∠1=54°,∠2
,∠3
,∠4各是多少度
?
解:
∵∠1=54°,
∴
∠2=∠1=54°.
∵a∥b,
∴
∠2+∠3=180°(两直线平行,同旁内角互补),
∴
∠3=180°-∠2=180°-54°=126°.
∵a∥b
,
∴∠4=∠2=54°(两直线平行,内错角相等).
检测目标
9.如图,已知∠1+∠2=180°,∠B=∠3,
判断∠C与∠AED的大小关系,并说明理由.
1
3
2
A
B
C
D
E
F
G
解:∠C=∠AED,理由是:
∵∠1+∠2=180°(已知)
∠1+∠EFD=180°(邻补角的定义)
∴∠2=∠EFD(同角的补角相等)
∴AB∥EF(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
∵∠B=∠3(已知)
∴∠ADE=∠B(等量代换)
∴DE∥BC(同位角相等,两直线平行)
∴∠C=∠AED(两直线平行,同位角相等)
检测目标
D
C
E
F
A
A
G
G
1
2
10.小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
挑战无处不在
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
温故知新
1.什么是平行线?
2.平行线的判定方法有哪些?
平行线的判定方法
同位角相等,
两直线平行。
内错角相等,
两直线平行。
同旁内角互补,
两直线平行。
这些判定方法先知道什么,后知道什么?
如果两条直线平行,那么这两条平行线被第三条直线所截而成的8个角会有什么关系呢?
5.3.1
平行线的性质
人教版七年级数学
下册
目标导航
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补。
2.能够根据平行线的性质进行简单的推理。
3.运用平行线的性质和判定进行简单的推理和计算。
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
思考
通过上题可知平行线的判定方法是什么?
探究
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
活动
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角.
度量所形成的8个角的度数,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
b
1
2
a
c
5
6
7
8
3
4
一、平行线的基本性质1
目标导学一:平行线的性质
观察
∠1~
∠8中,哪些是同位角?它们的度数
之间有什么关系?说出你的猜想:
猜想
两条平行线被第三条直线所截,同位角___.
相等
b
1
2
a
c
5
6
7
8
3
4
a
b
d
再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?
如果两直线不平行,上述结论还成立吗?
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
归纳
如图,已知a∥b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
解:
∵a∥b
(已知),
∴?1=?2(两直线平行,同位角相等).
∵
?1+?4=180°(邻补角定义),
∴?2+?4=180°(等量代换).
精典例题
思考:在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等,
能否得到内错角之间的数量关系?
二、平行线的基本性质2
如图:已知a//b,那么?2与?3相等吗?
为什么?
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵
∠1=∠3(对顶角相等),
∴
∠2=∠3(等量代换).
b
1
2
a
c
3
思考
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
∴∠ABD=∠BDC(两直线平行,内错角相等)
证明:∵AB∥CD(已知)
∵AE∥BD(
已知)
∴∠BDC=∠E
(两直线平行,同位角相等)
∴∠ABD=∠E(等量代换)
如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
精典例题
如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?
B
C
即学即练
如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?
B
C
答:∠C=142o
即学即练
如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?
B
C
答:∠C=142o
因为拐弯前后的两条路互相平行,∠B和∠C是两条平行线的内错角,根据两直线平行,内错角相等,∠C=∠B=142o
即学即练
如图,已知a//b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
解:
∵a//b
(已知),
∴?
1=
?
2
(两直线平行,同位角相等).
∵
?
1+
?
4=180°
(邻补角的性质),
∴?
2+
?
4=180°
(等量代换).
思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
三、平行线的基本性质3
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
∴?
2+
?
4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
例:如图,梯形ABCD中,AB//CD,∠D=(
)
A.
120°
B.
135°
C.
145°
D.
155°
B
精典例题
例:如图,
AB//CD,AD//BC.
求证:∠A=∠C.
证明:∵AB//CD(已知),
∴∠A+∠D=180°(两直线平行,同旁内角互补).
∵AD//BC(已知),
∴∠C+∠D=180°(两直线平行,同旁内角互补).
∴∠A=∠C(同角的补角相等).
即学即练
图形
已知
结果
结论
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
2
∠1=
∠2
∠3=
∠2
∠4+
∠2=1800
知识归纳
你能区别平行线的判定与性质吗?
四、平行线的判定与性质
同位角相等
内错角相等
同旁内角互补
两直线平行。
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
性质
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
性质
平行线的判定是先知道角相等或互补,后知道两直线平行。
你能区别平行线的判定与性质吗?
同位角相等
内错角相等
同旁内角互补
两直线平行。
判定
性质
平行线的判定是先知道角相等或互补,后知道两直线平行。
平行线的性质是先知道两直线平行,后知道角相等或互补。
你能区别平行线的判定与性质吗?
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的性质与判断的关系
例:如图,已知平行线AB、CD被直线AE所截
(1)从
∠1=110o可以知道∠2
是多少度吗,为什么?
(2)从∠1=110o可以知道
∠3是多少度吗,为什么?
(3)从
∠1=110o可以知道∠4
是多少度吗,为什么?
2
3
E
1
4
A
B
D
C
解:(1)∠2=110o
∵两直线平行,内错角相等;
(2)∠3=110o
∵两直线平行,
同位角相等;
(3)∠4=70o
∵两直线平行,同旁内角互补.
精典例题
例:如图,一条公路两次拐弯的前后两条路互相平行。第
一次拐弯时∠B是142°,第二次拐弯时∠C是多少度?
为什么?
解:∠C=142o
∵两直线平行,内错角相等.
B
C
精典例题
思维拓展:如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3,
∵两直线行,内错角相等;
∵∠1=∠2=∠3=∠4,
∴
∠5=∠6,
∴进入潜望镜的光线和
离开潜望镜的光线平行.
例1:如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B
=
60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
C
解:(1)
DE∥BC.理由如下:
∵
∠ADE=60°,∠B
=
60°
∴
∠ADE=∠B
∴
DE∥BC
(同位角相等,两直线平行
).
A
B
D
E
目标导学二:平行线的性质和判定及其综合应用
例:如下图一块梯形贴片的残余部分,量的∠A=100°,∠B=115°,另外两个角分别是多少度?
A
B
C
D
解:∵该四边形ABCD是梯形
∴AB∥CD
∴∠A+∠D=180°
∠B+∠C=180°(两直线平行,同旁内角互补)
∴
∠D=180°-
∠A
=
180°-
100°=80°
∠C=180°-
∠B
=
180°-
115°=65°
所以梯形的另外两个角分别是80°、65°
例:如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,
梯形另外两个角分别是多少度?
①梯形这个条件说明
∥
.
②∠A与∠D、∠B
与∠C的位置关系是
,
数量关系是
.
③所以∠D=
,∠C=
.
同旁内角
互补
80°
65°
DC
AB
已知:AB∥CD,∠1
=
∠2.试说明:BE∥CF.
证明:
∵AB
∥
CD
∴∠ABC=∠BCD
(两直线平行,内错角相等)
∵∠1=∠2
∴∠ABC
-∠1=∠BCD-
∠2
即∠3=∠4
∴
BE∥CF
(内错角相等,两直线平行)
即学既练
1
它与地面所
成的较大的
角是多少度
95
0
目前,它与地面所成的较小的角
为∠1=85?
2
3
联系生活
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
课堂小结
判定:已知角的关系得平行的关系.
推平行,用判定.
性质:已知平行的关系得角的关系.
知平行,用性质.
平行线的“判定”与“性质”有什么不同:
课堂小结
1.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14°
B.15°
C.16°
D.17°
C
检测目标
2.
如图,直线a//b,直线c与直线a,b相交,
若∠1=56°,则∠2等于(
)
A.
24°
B.
34°
C.
56°
D.
124°
C
检测目标
3.如图,∠BCD=95°,AB∥DE,则∠α与∠β满足(
)
A.∠α+∠β=95°
B.∠β﹣∠α=95°
C.∠α+∠β=85°
D.∠β﹣∠α=85°
【答案】D
【详解】
解:过点C作CF∥AB
∵AB∥DE,CF∥AB∴AB∥DE∥CF
∴∠BCF=∠α,∠DCF+∠β=180°
∴∠BCD=∠BCF
+∠DCF
∴∠α+180°-∠β=95°
∴∠β﹣∠α=85°故选:D
检测目标
4.如图,AB∥CD,则,,则的大小是(
)
A.
B.
C.
D.
【答案】B
【详解】
∵∠DEC=100°,∠C=40°,
∴∠D=180°-∠DEC-∠C=40°,
又∵AB∥CD,
∴∠B=∠D=40°,
故选B.
检测目标
5.如图,已知直线a,b被直线c所截,在括号内为下面各小题推理填上适当的根据:
(1)∵
a∥b,
∴∠1=∠3(
).
a
b
c
1
2
3
4
两直线平行,同位角相等
(2)∵
∠1=
∠3,
∴a∥b(
).
同位角相等,两直线平行
(3)∵a∥b
,
∴∠1=∠2(
).
两直线平行,内错角相等
检测目标
6.如图,BCD是一条直线,∠A=75°,
∠1=53°,∠2=75°,求∠B的度数.
B
A
C
D
E
1
2
解:
∵∠A=∠2=75°,
∴AB∥CE,
∴∠B=∠1=53°.
检测目标
7.已知:AB∥CD,∠1
=
∠2.试说明:BE∥CF.
证明:
∵AB
∥
CD(已知)
∴∠ABC=∠BCD
(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠ABC
-∠1=∠BCD-
∠2(等式性质)
即∠3=∠4
∴
BE∥CF(内错角相等,两直线平行)
1
2
4
3
检测目标
8.如图,直线a∥b,∠1=54°,∠2
,∠3
,∠4各是多少度
?
解:
∵∠1=54°,
∴
∠2=∠1=54°.
∵a∥b,
∴
∠2+∠3=180°(两直线平行,同旁内角互补),
∴
∠3=180°-∠2=180°-54°=126°.
∵a∥b
,
∴∠4=∠2=54°(两直线平行,内错角相等).
检测目标
9.如图,已知∠1+∠2=180°,∠B=∠3,
判断∠C与∠AED的大小关系,并说明理由.
1
3
2
A
B
C
D
E
F
G
解:∠C=∠AED,理由是:
∵∠1+∠2=180°(已知)
∠1+∠EFD=180°(邻补角的定义)
∴∠2=∠EFD(同角的补角相等)
∴AB∥EF(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
∵∠B=∠3(已知)
∴∠ADE=∠B(等量代换)
∴DE∥BC(同位角相等,两直线平行)
∴∠C=∠AED(两直线平行,同位角相等)
检测目标
D
C
E
F
A
A
G
G
1
2
10.小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法可以测出∠A的度数?
挑战无处不在
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
