2.4.2 二次函数的应用 课件(共30张PPT)
文档属性
| 名称 | 2.4.2 二次函数的应用 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 18:25:09 | ||
图片预览









文档简介
第4节 二次函数的应用
(第2课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.
2.学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.
学习目标
前面我们已经学习了利用二次函数解决几何最值问题,实际问题中最值问题,本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
新课导入
实际中二次函数模型的建立
知识点一
2.利用二次函数解决实际问题的基本思路是:
(1)建立适当的平面直角坐标系;
(2)把实际问题中一些数据与点的坐标联系起来;
(3)用待定系数法求出抛物线对应的函数表达式;
(4)利用二次函数的图象及性质去分析、解决问题.
探究新知
例1 图中是抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
例题讲解
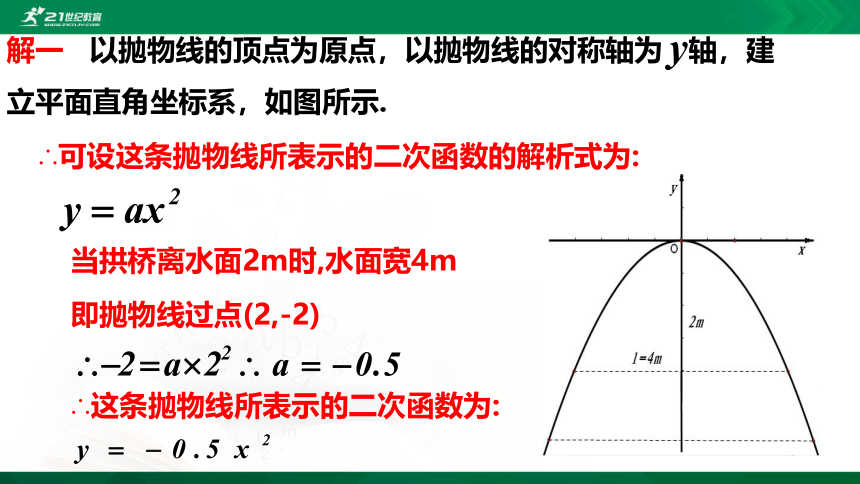
解一 以抛物线的顶点为原点,以抛物线的对称轴为 轴,建立平面直角坐标系,如图所示.
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
当水面下降1m时,水面的纵坐标为y=-3,这时有:
∴当水面下降1m时,水面宽度增加了
解二 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
∴这条抛物线所表示的二次函数为:
∴可设这条抛物线所表示的二次函数的解析式为:
此时,抛物线的顶点为(0,2)
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
总结:求解的一般步骤是:
1.建立适当的平面直角坐标系,将抛物线形状的图形放在坐标中;
2. 结合图形和已知条件,分析变量间的关系;
3. 用待定系数法求函数表达式;
4. 利用二次函数的表达式及其性质,求解实际问题.
求实际中“抛物线”型的最值问题
知识点二
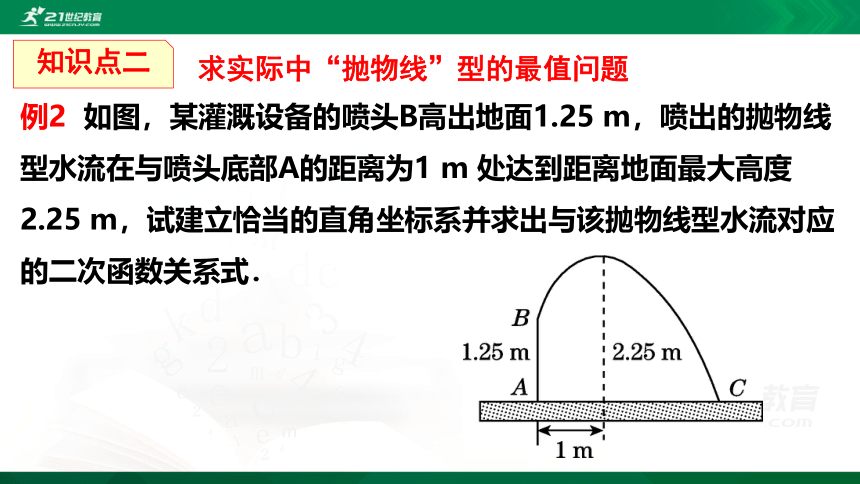
例2 如图,某灌溉设备的喷头B高出地面1.25 m,喷出的抛物线型水流在与喷头底部A的距离为1 m 处达到距离地面最大高度2.25 m,试建立恰当的直角坐标系并求出与该抛物线型水流对应的二次函数关系式.
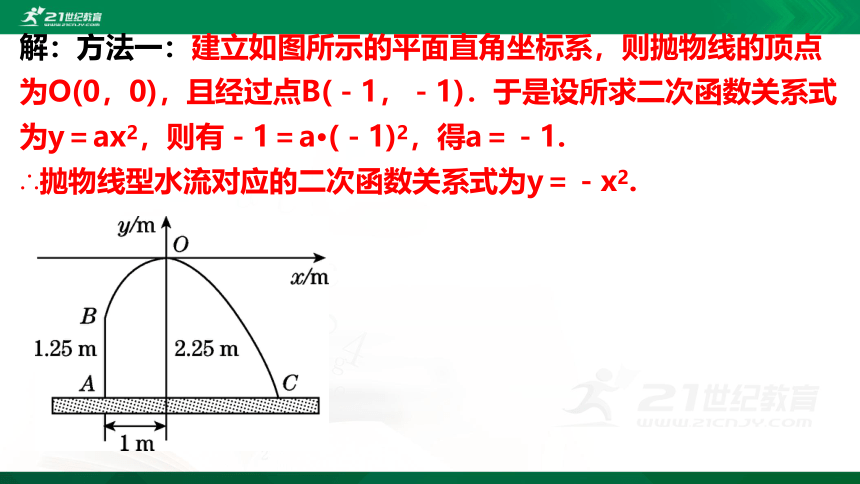
解:方法一:建立如图所示的平面直角坐标系,则抛物线的顶点为O(0,0),且经过点B(-1,-1).于是设所求二次函数关系式为y=ax2,则有-1=a·(-1)2,得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2.
方法二:建立如图所示的平面直角坐标系,则抛物线的顶点为D(0,2.25),且抛物线经过点B(-1,1.25).于是设所求二次函数关系式为y=ax2+2.25,则有1.25=a·(-1)2+2.25,解得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2+2.25.
方法三:建立如图所示的平面直角坐标系,则抛物线的顶点为D(1,2.25),且经过点B(0,1.25).于是设所求二次函数关系式为y=a(x-1)2+2.25,则有1.25=a(-1)2+2.25,解得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-(x-1)2+2.25.
总结:解决抛物线型问题,其一般步骤为:
(1)建立适当的坐标系,正确写出关键点的坐标;
(2)根据图象设抛物线对应的函数表达式;
(3)根据已知条件,利用待定系数法求表达式,再利用二次函数的性质解题.在解题过程中要充分利用抛物线的对称性,同时要注意数形结合思想的应用.
用二次函数表达式表示实际问题
知识点三
根据实际问题列二次函数的关系式,一般要经历以下几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
例3 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合.问题:
(1)试写出重叠部分面积y(cm2)与线段MA的
长度x(cm)之间的函数关系式;
(2)当MA=1 cm时,重叠部分的面积是多少?
例题讲解
解:(1)由题意知,开始时A点与M点重合,让△ABC向右
移动,两图形重叠部分为等腰直角三角形,
所以y= x2(0<x≤10);
(2)当MA=1 cm时,重叠部分的面积是 cm2.
利用二次函数求实际应用中的最值问题
知识点四
例4 服装厂生产某品牌的T恤衫成本
是每件10元.根据市场调查,以单价
13元批发给经销商,经销商愿意经销
5 000件,并且表示单价每降价0.1元,
愿意多经销500件.
请你帮助分析,厂家批发单价是多少时可以获利最多?
解: 设每件T恤降价 0.1x 元时,获利 y 元.
=-50x2+1000x+15000
y=(13-10-0.1x)(5000+500x)
=-50(x-10)2+20000
当x=10时,获利最多,为20000元.
此时单价为13-10×0.1=12元
总结: 利用二次函数解决实际生活中的利润问题,一般运用“总利润=每件商品所获利润×销售件数”或“总利润=总售价-总成本”建立利润与销售单价之间的二次函数关系式,求其图象的顶点坐标,获取最值.
1 河北省赵县的赵州桥的桥拱是近似的抛物线型,建立如图所示的平面直角坐标系,其函数表达式为 y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB为( )
A.-20 m B.10 m C.20 m D.-10 m
课堂练习
2 某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:m)的一部分,则水喷出的最大高度是( )
A.4 m B.5 m
C.6 m D.7 m
3 心理学家发现:学生对概念的接受能力y与提出概念的时间x(min)之间是二次函数关系,当提出概念13min时,学生对概念的接受能力最大,为59.9;当提出概念30 min时,学生对概念的接受能力就剩下31,则y与x满足的二次函数表达式为( )
A.y=-(x-13)2+59.9
B.y=-0.1x2+2.6x+31
C.y=0.1x2-2.6x+76.8
D.y=-0.1x2+2.6x+43
4 向上发射一枚炮弹,经x s后的高度为y m,且时间与高度之间的关系为y=ax2+bx.若此炮弹在第7 s与第14 s时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9.5 s B.第10 s
C.第10.5 s D.第11 s
5 如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时抛物线对应的函数表达式是y=- (x-6)2+4,则选取点B为坐标原点时抛物线对应的函数表达式是____________.
6 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可 售出400件. 根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提 高1元,销售量相应减少20件. 销售单价为多少元时,半月内获得的利润最大?最大利润是多少?
1.抛物线型建筑物问题:几种常见的抛物线型建筑物有拱形桥洞、隧道洞口、拱形门等.解决这类问题的关键是根据已知条件选择合理的位置建立直角坐标系,结合问题中的数据求出函数解析式,然后利用函数解析式解决问题.
利润问题的基本关系式:
总利润=单件利润×销售总量.
若销售单价每提高m元,销售量相应减少n件,
设提高x元,则现销售量=原销售量-
课堂小结
谢谢聆听
(第2课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.
2.学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.
学习目标
前面我们已经学习了利用二次函数解决几何最值问题,实际问题中最值问题,本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
新课导入
实际中二次函数模型的建立
知识点一
2.利用二次函数解决实际问题的基本思路是:
(1)建立适当的平面直角坐标系;
(2)把实际问题中一些数据与点的坐标联系起来;
(3)用待定系数法求出抛物线对应的函数表达式;
(4)利用二次函数的图象及性质去分析、解决问题.
探究新知
例1 图中是抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
例题讲解
解一 以抛物线的顶点为原点,以抛物线的对称轴为 轴,建立平面直角坐标系,如图所示.
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
当水面下降1m时,水面的纵坐标为y=-3,这时有:
∴当水面下降1m时,水面宽度增加了
解二 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
∴这条抛物线所表示的二次函数为:
∴可设这条抛物线所表示的二次函数的解析式为:
此时,抛物线的顶点为(0,2)
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
总结:求解的一般步骤是:
1.建立适当的平面直角坐标系,将抛物线形状的图形放在坐标中;
2. 结合图形和已知条件,分析变量间的关系;
3. 用待定系数法求函数表达式;
4. 利用二次函数的表达式及其性质,求解实际问题.
求实际中“抛物线”型的最值问题
知识点二
例2 如图,某灌溉设备的喷头B高出地面1.25 m,喷出的抛物线型水流在与喷头底部A的距离为1 m 处达到距离地面最大高度2.25 m,试建立恰当的直角坐标系并求出与该抛物线型水流对应的二次函数关系式.
解:方法一:建立如图所示的平面直角坐标系,则抛物线的顶点为O(0,0),且经过点B(-1,-1).于是设所求二次函数关系式为y=ax2,则有-1=a·(-1)2,得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2.
方法二:建立如图所示的平面直角坐标系,则抛物线的顶点为D(0,2.25),且抛物线经过点B(-1,1.25).于是设所求二次函数关系式为y=ax2+2.25,则有1.25=a·(-1)2+2.25,解得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2+2.25.
方法三:建立如图所示的平面直角坐标系,则抛物线的顶点为D(1,2.25),且经过点B(0,1.25).于是设所求二次函数关系式为y=a(x-1)2+2.25,则有1.25=a(-1)2+2.25,解得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-(x-1)2+2.25.
总结:解决抛物线型问题,其一般步骤为:
(1)建立适当的坐标系,正确写出关键点的坐标;
(2)根据图象设抛物线对应的函数表达式;
(3)根据已知条件,利用待定系数法求表达式,再利用二次函数的性质解题.在解题过程中要充分利用抛物线的对称性,同时要注意数形结合思想的应用.
用二次函数表达式表示实际问题
知识点三
根据实际问题列二次函数的关系式,一般要经历以下几个步骤:
(1)确定自变量与因变量代表的实际意义;
(2)找到自变量与因变量之间的等量关系,根据等量关系列出方程或等式.
(3)将方程或等式整理成二次函数的一般形式.
例3 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合.问题:
(1)试写出重叠部分面积y(cm2)与线段MA的
长度x(cm)之间的函数关系式;
(2)当MA=1 cm时,重叠部分的面积是多少?
例题讲解
解:(1)由题意知,开始时A点与M点重合,让△ABC向右
移动,两图形重叠部分为等腰直角三角形,
所以y= x2(0<x≤10);
(2)当MA=1 cm时,重叠部分的面积是 cm2.
利用二次函数求实际应用中的最值问题
知识点四
例4 服装厂生产某品牌的T恤衫成本
是每件10元.根据市场调查,以单价
13元批发给经销商,经销商愿意经销
5 000件,并且表示单价每降价0.1元,
愿意多经销500件.
请你帮助分析,厂家批发单价是多少时可以获利最多?
解: 设每件T恤降价 0.1x 元时,获利 y 元.
=-50x2+1000x+15000
y=(13-10-0.1x)(5000+500x)
=-50(x-10)2+20000
当x=10时,获利最多,为20000元.
此时单价为13-10×0.1=12元
总结: 利用二次函数解决实际生活中的利润问题,一般运用“总利润=每件商品所获利润×销售件数”或“总利润=总售价-总成本”建立利润与销售单价之间的二次函数关系式,求其图象的顶点坐标,获取最值.
1 河北省赵县的赵州桥的桥拱是近似的抛物线型,建立如图所示的平面直角坐标系,其函数表达式为 y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB为( )
A.-20 m B.10 m C.20 m D.-10 m
课堂练习
2 某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:m)的一部分,则水喷出的最大高度是( )
A.4 m B.5 m
C.6 m D.7 m
3 心理学家发现:学生对概念的接受能力y与提出概念的时间x(min)之间是二次函数关系,当提出概念13min时,学生对概念的接受能力最大,为59.9;当提出概念30 min时,学生对概念的接受能力就剩下31,则y与x满足的二次函数表达式为( )
A.y=-(x-13)2+59.9
B.y=-0.1x2+2.6x+31
C.y=0.1x2-2.6x+76.8
D.y=-0.1x2+2.6x+43
4 向上发射一枚炮弹,经x s后的高度为y m,且时间与高度之间的关系为y=ax2+bx.若此炮弹在第7 s与第14 s时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9.5 s B.第10 s
C.第10.5 s D.第11 s
5 如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时抛物线对应的函数表达式是y=- (x-6)2+4,则选取点B为坐标原点时抛物线对应的函数表达式是____________.
6 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可 售出400件. 根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提 高1元,销售量相应减少20件. 销售单价为多少元时,半月内获得的利润最大?最大利润是多少?
1.抛物线型建筑物问题:几种常见的抛物线型建筑物有拱形桥洞、隧道洞口、拱形门等.解决这类问题的关键是根据已知条件选择合理的位置建立直角坐标系,结合问题中的数据求出函数解析式,然后利用函数解析式解决问题.
利润问题的基本关系式:
总利润=单件利润×销售总量.
若销售单价每提高m元,销售量相应减少n件,
设提高x元,则现销售量=原销售量-
课堂小结
谢谢聆听
