六年级下册数学教案-2.1.1 圆柱(一)西师大版
文档属性
| 名称 | 六年级下册数学教案-2.1.1 圆柱(一)西师大版 |

|
|
| 格式 | doc | ||
| 文件大小 | 302.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 15:26:11 | ||
图片预览

文档简介
第二单元 圆柱
第一课时 圆柱(一)
圆柱的认识与圆柱的侧面积
学习内容:
教材24—25页例1、例2。
学习目标:
1.能知道圆柱各部分的名称,掌握圆柱的基本特征。
2.会描述圆柱侧面展开图与圆柱各部分的关系。
3.理解圆柱的侧面积的含义,探索圆柱侧面积的计算方法。
学习重、难点:
理解各个部分之间的关系,并以此学会求圆柱侧面积的方法。
学习过程:
一、学习准备。
1.这些物体的形状有什么共同特点?
2.生活中的物体,形状是圆柱形的有哪些,请用自己的话简单说一说并谈谈它都有哪些部分。
二、合作探究。
(一)自学例1,在完成自学后再在小组讨论下完成下面练习。
1.圆柱各部分名称及特征。
4467225200025(1)在观察我们不难发现:圆柱有两个 和一个 组成。圆柱的两个圆面叫做 ;周围的面叫做 ;两底面之间的距离叫做 。
(2)圆柱有什么特征?观察右图后在小组内说说自己的想法。
圆柱的特征:圆柱的两底面都是 ,并且大小 ;
圆柱的侧面是 ;有 条高,长度都相等。
(二)自学例2,在完成自学后再在小组讨论下完成下面练习。
1.圆柱的侧面、底面及之间的关系。
圆柱的侧面展开后是什么形状?请用纸做出一个圆柱体剪一剪再展开。
496252595250125920585725圆柱侧面展开后得到的长方形的长、宽与圆柱有什么关系?把这个长方形重新包在圆柱上,请说出你的发现。
圆柱侧面展开后得到的长方形的长、宽与圆柱有什么关系?把这个长方形重新包在圆柱上,请说出你的发现。
(1)在展开后我们发现,沿圆柱的高剪开侧面,侧面是 ,长方形的长等于圆柱 的 周长,长方形的宽等于圆柱的 。
(2)请用自己的语言概括圆柱的侧面、底面及之间的关系。
2.圆柱的侧面积。
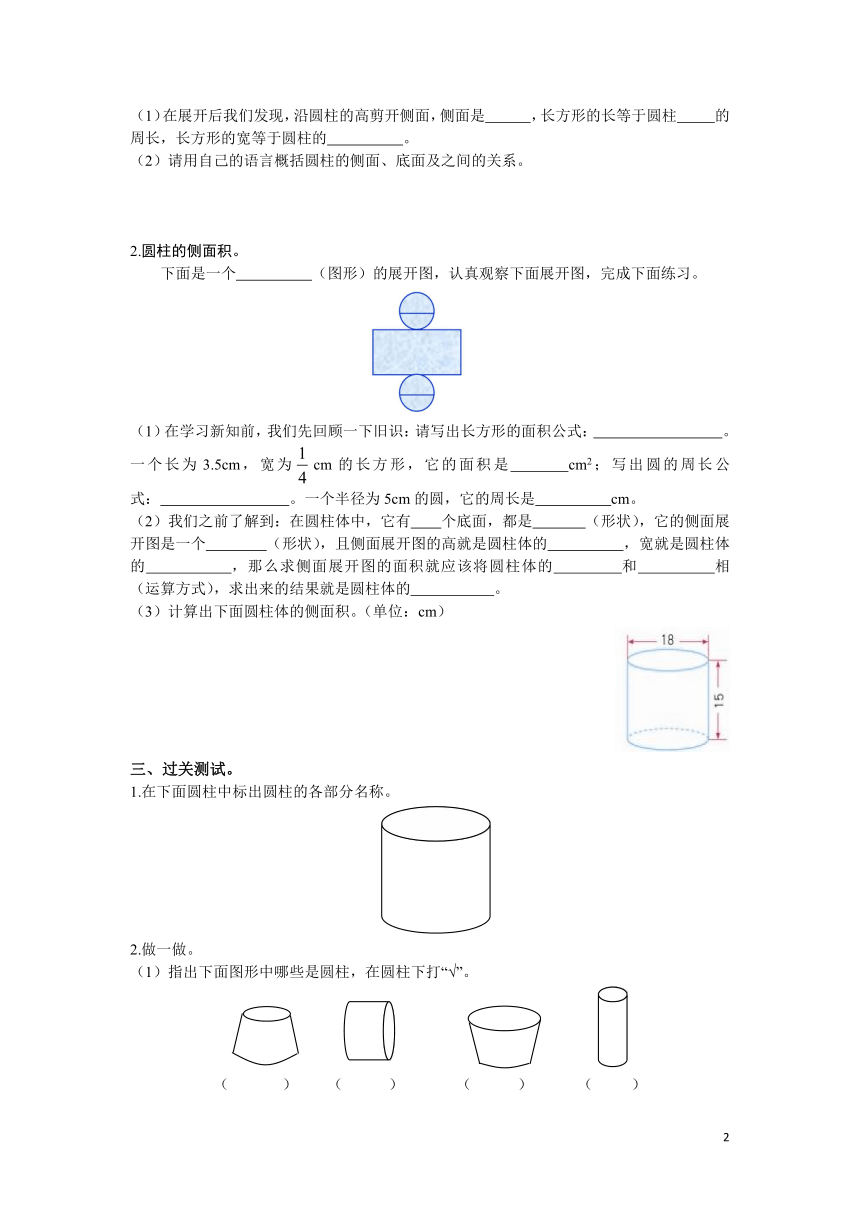
下面是一个 (图形)的展开图,认真观察下面展开图,完成下面练习。
(1)在学习新知前,我们先回顾一下旧识:请写出长方形的面积公式: 。一个长为3.5cm,宽为falsecm的长方形,它的面积是 cm2;写出圆的周长公式: 。一个半径为5cm的圆,它的周长是 cm。
(2)我们之前了解到:在圆柱体中,它有 个底面,都是 (形状),它的侧面展开图是一个 (形状),且侧面展开图的高就是圆柱体的 ,宽就是圆柱体的 ,那么求侧面展开图的面积就应该将圆柱体的 和 相 (运算方式),求出来的结果就是圆柱体的 。
(3)计算出下面圆柱体的侧面积。(单位:cm)
三、过关测试。
1.在下面圆柱中标出圆柱的各部分名称。
2.做一做。
(1)指出下面图形中哪些是圆柱,在圆柱下打“√”。
( ) ( ) ( ) ( )
3.判断。
(1)上下两个底面相等的物体一定是圆柱体。( )
(2)圆柱的侧面沿着高展开后,会得到一个长方形或者正方形。 ( )
(3)同一个圆柱底面之间的距离处处相等。( )
(4)一个圆柱,底面周长是12.56厘米,高是12.56厘米。这个圆柱的侧面沿着高展开,得到一个长方形。( )
(5)一个圆柱,底面半径是4厘米,高是4厘米。这个圆柱的侧面沿着高展开,得到一个正方形。( )
(6)圆柱的底面是两个大小相同的圆。( )
4.一个圆柱的侧面积是175.84平方分米,底面半径是2分米。它的高是多少分米?
5.一个圆柱的侧面积是188.84平方米,高是10米,它的底面半径是多少米?
6.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动一周,压路的面积是多少平方米?
7.广告公司制作了一个底面直径1.5m,高2.5m的圆柱形灯箱。它的侧面最多可以张贴多大面积的海报?
8.一个圆柱的侧面沿高展开是一个长12.56cm,宽6.28cm的长方形,求这个圆柱的底面半径。
四、课后反思。
第二课时 圆柱(二)
圆柱的表面积
学习内容:
教材25页例3。
学习目标:
1.能理解圆柱表面积的含义。
2.掌握圆柱表面积的计算方法。
3.能正确计算圆柱的表面积,并能解决生活中的实际问题。
学习重、难点:
能正确计算圆柱的表面积,并能解决生活中的实际问题。
学习过程:
一、学习准备。
1.填空。
(1)圆面积公式是: ;圆柱体侧面积公式是: 。
(2)圆柱的两底面都是 ,并且大小 ;圆柱的侧面是 ;长方形的长等于圆柱的 ,长方形的宽等于圆柱的 。
2.说说什么是“表面积”?
二、合作探究。
(一)自学例3,在完成自学后再在小组讨论下完成下面练习。
1.圆柱的表面积的意义及计算方法。
(1)根据学习准备可知,“圆柱的表面积”就是指圆柱的 和两个 的面积之和。
(2)计算圆柱的表面积。观察下面图形,完成下面练习,并小组探究如何计算圆柱的表面积?
我的发现:圆柱的表面积=圆柱的 +两个 的面积
圆柱的侧面积= × 【底面是 (形状),圆的面积公式是 】
所以,圆柱体的表面积公式是 。
2.计算圆柱的表面积。
【例】王阿姨做了一个圆柱形的抱枕,长80cm,底面直径18cm,共需要多少平方厘米的布?
3.变式训练。
5073650174625一顶圆柱形厨师帽,高30cm,帽顶直径20cm,做这样一顶帽子至少需要用多少平方厘米的面料?(得数保留整十数)
【小提示】根据上图及生活经验,我们可以发现,帽子、水桶等不同于我们平时练习用的圆柱体,因为它们只有 个底面、 个侧面,因此我们在计算其表面积时,则应该 ,才能得出正确结果。
三、过关测试。
1.用铁皮制作1节圆柱形通风管,它的长是60cm,底面直径是10cm。至少需要多少平方厘米铁皮?
2.一个圆柱形铁皮水桶(无盖),高12dm,底面直径是高的false。做这个水桶大约要用多少铁皮?
3.如图,林林做了一个圆柱形的灯笼。上下底面的中间留出了直径为10cm的圆口,他用了多少彩纸?
4.为迎接国庆,学校把大厅柱子布置成花柱,花柱的高是3.8米,底面半径是0.5米,如果每平方米有45朵花,这根柱子上有多少朵花?
四、课后反思。
第一课时 圆柱(一)
圆柱的认识与圆柱的侧面积
学习内容:
教材24—25页例1、例2。
学习目标:
1.能知道圆柱各部分的名称,掌握圆柱的基本特征。
2.会描述圆柱侧面展开图与圆柱各部分的关系。
3.理解圆柱的侧面积的含义,探索圆柱侧面积的计算方法。
学习重、难点:
理解各个部分之间的关系,并以此学会求圆柱侧面积的方法。
学习过程:
一、学习准备。
1.这些物体的形状有什么共同特点?
2.生活中的物体,形状是圆柱形的有哪些,请用自己的话简单说一说并谈谈它都有哪些部分。
二、合作探究。
(一)自学例1,在完成自学后再在小组讨论下完成下面练习。
1.圆柱各部分名称及特征。
4467225200025(1)在观察我们不难发现:圆柱有两个 和一个 组成。圆柱的两个圆面叫做 ;周围的面叫做 ;两底面之间的距离叫做 。
(2)圆柱有什么特征?观察右图后在小组内说说自己的想法。
圆柱的特征:圆柱的两底面都是 ,并且大小 ;
圆柱的侧面是 ;有 条高,长度都相等。
(二)自学例2,在完成自学后再在小组讨论下完成下面练习。
1.圆柱的侧面、底面及之间的关系。
圆柱的侧面展开后是什么形状?请用纸做出一个圆柱体剪一剪再展开。
496252595250125920585725圆柱侧面展开后得到的长方形的长、宽与圆柱有什么关系?把这个长方形重新包在圆柱上,请说出你的发现。
圆柱侧面展开后得到的长方形的长、宽与圆柱有什么关系?把这个长方形重新包在圆柱上,请说出你的发现。
(1)在展开后我们发现,沿圆柱的高剪开侧面,侧面是 ,长方形的长等于圆柱 的 周长,长方形的宽等于圆柱的 。
(2)请用自己的语言概括圆柱的侧面、底面及之间的关系。
2.圆柱的侧面积。
下面是一个 (图形)的展开图,认真观察下面展开图,完成下面练习。
(1)在学习新知前,我们先回顾一下旧识:请写出长方形的面积公式: 。一个长为3.5cm,宽为falsecm的长方形,它的面积是 cm2;写出圆的周长公式: 。一个半径为5cm的圆,它的周长是 cm。
(2)我们之前了解到:在圆柱体中,它有 个底面,都是 (形状),它的侧面展开图是一个 (形状),且侧面展开图的高就是圆柱体的 ,宽就是圆柱体的 ,那么求侧面展开图的面积就应该将圆柱体的 和 相 (运算方式),求出来的结果就是圆柱体的 。
(3)计算出下面圆柱体的侧面积。(单位:cm)
三、过关测试。
1.在下面圆柱中标出圆柱的各部分名称。
2.做一做。
(1)指出下面图形中哪些是圆柱,在圆柱下打“√”。
( ) ( ) ( ) ( )
3.判断。
(1)上下两个底面相等的物体一定是圆柱体。( )
(2)圆柱的侧面沿着高展开后,会得到一个长方形或者正方形。 ( )
(3)同一个圆柱底面之间的距离处处相等。( )
(4)一个圆柱,底面周长是12.56厘米,高是12.56厘米。这个圆柱的侧面沿着高展开,得到一个长方形。( )
(5)一个圆柱,底面半径是4厘米,高是4厘米。这个圆柱的侧面沿着高展开,得到一个正方形。( )
(6)圆柱的底面是两个大小相同的圆。( )
4.一个圆柱的侧面积是175.84平方分米,底面半径是2分米。它的高是多少分米?
5.一个圆柱的侧面积是188.84平方米,高是10米,它的底面半径是多少米?
6.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动一周,压路的面积是多少平方米?
7.广告公司制作了一个底面直径1.5m,高2.5m的圆柱形灯箱。它的侧面最多可以张贴多大面积的海报?
8.一个圆柱的侧面沿高展开是一个长12.56cm,宽6.28cm的长方形,求这个圆柱的底面半径。
四、课后反思。
第二课时 圆柱(二)
圆柱的表面积
学习内容:
教材25页例3。
学习目标:
1.能理解圆柱表面积的含义。
2.掌握圆柱表面积的计算方法。
3.能正确计算圆柱的表面积,并能解决生活中的实际问题。
学习重、难点:
能正确计算圆柱的表面积,并能解决生活中的实际问题。
学习过程:
一、学习准备。
1.填空。
(1)圆面积公式是: ;圆柱体侧面积公式是: 。
(2)圆柱的两底面都是 ,并且大小 ;圆柱的侧面是 ;长方形的长等于圆柱的 ,长方形的宽等于圆柱的 。
2.说说什么是“表面积”?
二、合作探究。
(一)自学例3,在完成自学后再在小组讨论下完成下面练习。
1.圆柱的表面积的意义及计算方法。
(1)根据学习准备可知,“圆柱的表面积”就是指圆柱的 和两个 的面积之和。
(2)计算圆柱的表面积。观察下面图形,完成下面练习,并小组探究如何计算圆柱的表面积?
我的发现:圆柱的表面积=圆柱的 +两个 的面积
圆柱的侧面积= × 【底面是 (形状),圆的面积公式是 】
所以,圆柱体的表面积公式是 。
2.计算圆柱的表面积。
【例】王阿姨做了一个圆柱形的抱枕,长80cm,底面直径18cm,共需要多少平方厘米的布?
3.变式训练。
5073650174625一顶圆柱形厨师帽,高30cm,帽顶直径20cm,做这样一顶帽子至少需要用多少平方厘米的面料?(得数保留整十数)
【小提示】根据上图及生活经验,我们可以发现,帽子、水桶等不同于我们平时练习用的圆柱体,因为它们只有 个底面、 个侧面,因此我们在计算其表面积时,则应该 ,才能得出正确结果。
三、过关测试。
1.用铁皮制作1节圆柱形通风管,它的长是60cm,底面直径是10cm。至少需要多少平方厘米铁皮?
2.一个圆柱形铁皮水桶(无盖),高12dm,底面直径是高的false。做这个水桶大约要用多少铁皮?
3.如图,林林做了一个圆柱形的灯笼。上下底面的中间留出了直径为10cm的圆口,他用了多少彩纸?
4.为迎接国庆,学校把大厅柱子布置成花柱,花柱的高是3.8米,底面半径是0.5米,如果每平方米有45朵花,这根柱子上有多少朵花?
四、课后反思。
