2.5 一元一次不等式与一次函数一课一练(含解析)
文档属性
| 名称 | 2.5 一元一次不等式与一次函数一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 17:40:13 | ||
图片预览


文档简介
初中数学北师大版八年级下学期 第二章 2.5 一元一次不等式与一次函数
一、单选题
1.如图,直线 与坐标轴相交于 , 两点,则关于x的不等式 的解集是(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
2.直线 : 与直线 : 在同一平面直角坐标系中的图象如图所示,则关于 的不等式 的解为(??? )
A.?x>-1???????????????????????????????B.?x<-1???????????????????????????????C.? x<-2???????????????????????????????D.?无法确定
3.如图,一次函数y=kx+b的图象与y轴交于点(0,1),则关于x的不等式kx+b>1的解集是(? )
A.?x>0????????????????????????????????????B.?x<0????????????????????????????????????C.?x>1????????????????????????????????????D.?x<1
4.如图,一次函数 ( )的图像与正比例函数 ( )的图像相交于点 ,已知点 的横坐标为1,则关于 的不等式 的解集为(? )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
5.已知一次函数y=kx+b中,x取不同值时,y对应的值列表如下:
x
…
-m2-1
2
3
…
y
…
-1
0
n2+1
…
则不等式kx+b>0(其中k,b,m,n为常数)的解集为( ??)
A.?x>2??????????????????????????????????B.?x>3??????????????????????????????????C.?x<2??????????????????????????????????D.?无法确定
6.同一平面直角坐标系中,一次函数 的图像与正比例函数 的图像如图所示,则关于 的方程 的解为(????? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
7.如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为(? ??)
A.?x>﹣2????????????????????????????????B.?x<﹣2????????????????????????????????C.?x>﹣5????????????????????????????????D.?x<﹣5
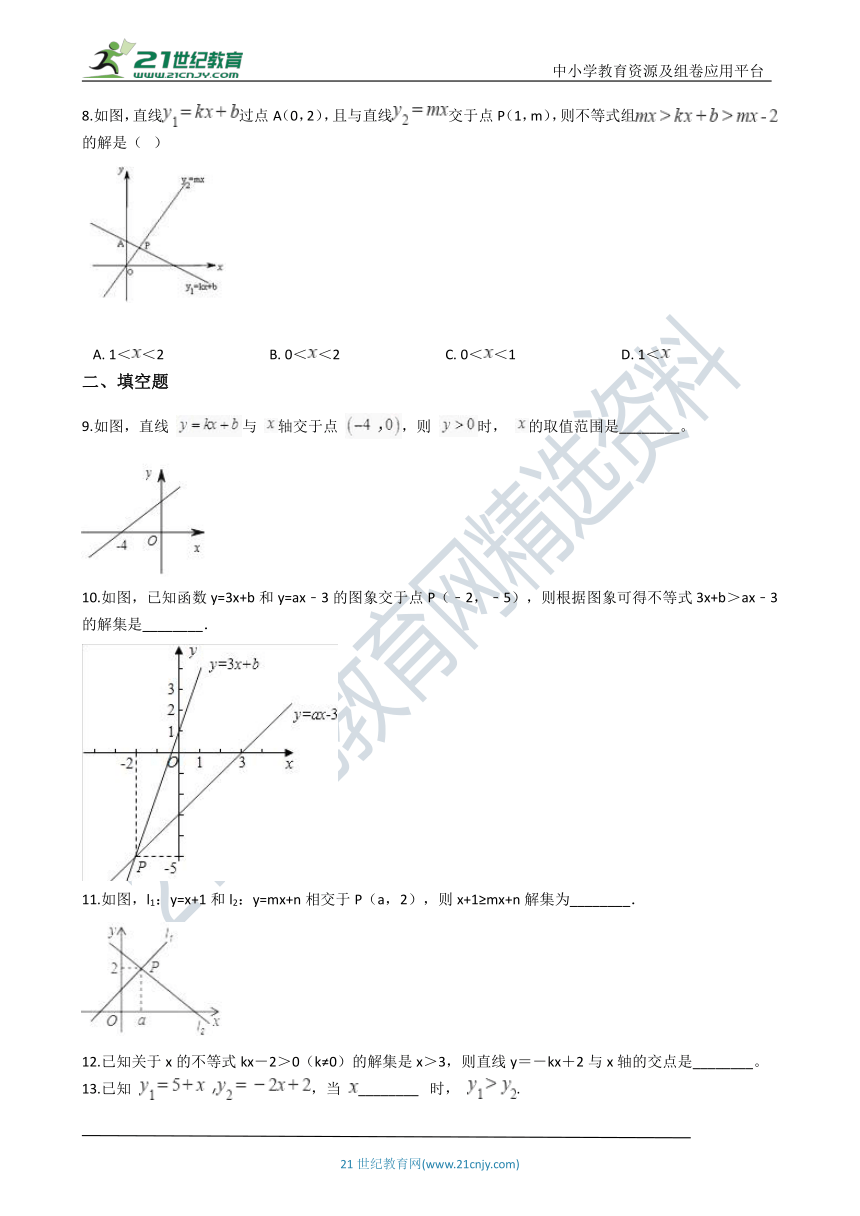
8.如图,直线过点A(0,2),且与直线交于点P(1,m),则不等式组的解是(???)
A.?1<<2??????????????????????????????B.?0<<2??????????????????????????????C.?0<<1??????????????????????????????D.?1<
二、填空题
9.如图,直线 与 轴交于点 ,则 时, 的取值范围是________。
10.如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是________.
11.如图,l1:y=x+1和l2:y=mx+n相交于P(a,2),则x+1≥mx+n解集为________.
12.已知关于x的不等式kx-2>0(k≠0)的解集是x>3,则直线y=-kx+2与x轴的交点是________。
13.已知 ,当 ________? 时, .
三、解答题
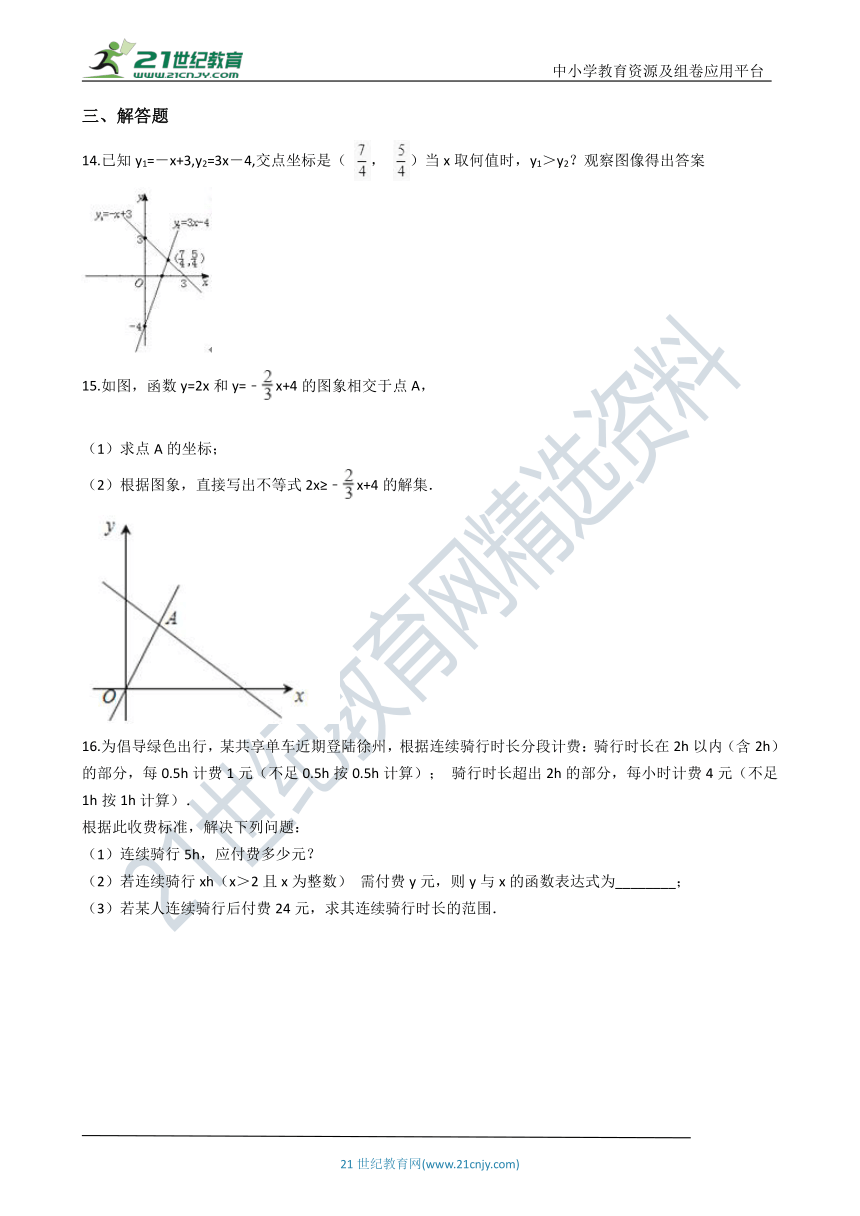
14.已知y1=-x+3,y2=3x-4,交点坐标是( , )当x取何值时,y1>y2?观察图像得出答案
15.如图,函数y=2x和y=﹣x+4的图象相交于点A,
(1)求点A的坐标;
(2)根据图象,直接写出不等式2x≥﹣x+4的解集.
16.为倡导绿色出行,某共享单车近期登陆徐州,根据连续骑行时长分段计费:骑行时长在2h以内(含2h)的部分,每0.5h计费1元(不足0.5h按0.5h计算); 骑行时长超出2h的部分,每小时计费4元(不足1h按1h计算).
根据此收费标准,解决下列问题:
(1)连续骑行5h,应付费多少元?
(2)若连续骑行xh(x>2且x为整数) 需付费y元,则y与x的函数表达式为________;
(3)若某人连续骑行后付费24元,求其连续骑行时长的范围.
答案解析部分
一、单选题
1.【答案】 D
解:∵直线y=kx+b交x轴于A(-2,0),
结合函数图形可知不等式kx+b>0解集对应直线在x轴上方部分图象上点的横坐标的集合;
∴不等式kx+b>0的解集是x>-2,
故答案为:D.
2.【答案】 B
解:通过观察函数图像可知要使 需要看图像在上方时候横坐标的取值范围,可以得出当x<-1时候满足条件;故答案是B选项
3.【答案】 B
解:由一次函数的图象可知,此函数是减函数,
?????????????????? ∵一次函数y=kx+b的图象与y轴交于点(0,1),
?????????????????? ∴当x<0时,关于x的不等式kx+b>1.
故选B.
4.【答案】A
解:当x<1时,kx+3>mx,所以关于x的不等式(k-m)x>-3的解集为x<1.故答案为:A.
5.【答案】 A
解:由表格可得:x=2时,y=0,由n2+1>0,
则x>2时,不等式kx+b>0(其中k,b,m,n为常数).
故答案为:A.
6.【答案】 D
解:y=k1x?2b=k1x+b?3b是由y=k1x+b向上平移?3b个单位得到的,
∵y=k1x+b与y=k2x交点的横坐标为?2,
∴y=k1x?2b与y=k2x的交点的横坐标为4,
∴方程k1x?2b>k2x的解为:x<4.
故选:D.
7.【答案】 A
解:从图像得到,当x>﹣2时,y1=3x+b的图像对应的点在函数y2=ax﹣3的图像上面,
∴不等式3x+b>ax﹣3的解集为:x>﹣2.
故答案为:A.
8.【答案】 A
解:由于一次函数y1同时经过A、P两点,可将它们的坐标分别代入y1的解析式中,即可求得k、b与m的关系,将其代入所求不等式组中,即可求得不等式的解集.
由于直线y1=kx+b过点A(0,2),P(1,m),
则有:
k+b=m
b=2
解得
k=m?2
b=2
∴直线y1=(m-2)x+2.
故所求不等式组可化为:mx>(m-2)x+2>mx-2,
解得:1<x<2.
9.【答案】
解:从图像可以观察当y大于0的时候,x的取值范围是 ,故答案是
10.【答案】x>﹣2
解:从图象得到,当x>﹣2时,y=3x+b的图象对应的点在函数y=ax﹣3的图象上面,
∴不等式3x+b>ax﹣3的解集为:x>﹣2.
故答案为:x>﹣2.
11.【答案】x≥1
解∵直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),
∴a+1=2,
解得:a=1,
观察图象知:关于x的不等式x+1≥mx+n的解集为x≥1.
12.【答案】(3,0)
解:因为不等式kx-2>0(k≠0)的解集是x>3,所以可以求得k的值是 ,将k的值代入y=-kx+2,得到y=- x+2 ,与x轴的交点是纵坐标是0,即0=- x+2,解得x=3,所以坐标是(3,0)
13.【答案】 x>-1
解:∵ ,
∴5+x>-2x+2
3x>-3
x>-1
故答案为:x>-1.
三、解答题
14.【答案】 若y1>y2 , 观察函数y1的图像在函数y2的上方,当x取小于 的值时,有y1>y2
解:若y1>y2 , 那么只需要观察函数y1的图像在函数y2的上方即可,当x取小于 的值时,有y1>y2
15.【答案】 解:(1)由, 解得:, ∴A的坐标为(, 3);(2)由图象,得不等式2x≥﹣x+4的解集为:x≥.
16.【答案】 (1)解:当x=5时,y=2×2+4×(5﹣2)=16,
∴应付16元。
(2)y=4(x﹣2)+2×2=4x﹣4;
故答案为:y=4x﹣4;
(3)当y=24,24=4x﹣4,
x=7,
∴连续骑行时长的范围是:6<x≤7
一、单选题
1.如图,直线 与坐标轴相交于 , 两点,则关于x的不等式 的解集是(??? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
2.直线 : 与直线 : 在同一平面直角坐标系中的图象如图所示,则关于 的不等式 的解为(??? )
A.?x>-1???????????????????????????????B.?x<-1???????????????????????????????C.? x<-2???????????????????????????????D.?无法确定
3.如图,一次函数y=kx+b的图象与y轴交于点(0,1),则关于x的不等式kx+b>1的解集是(? )
A.?x>0????????????????????????????????????B.?x<0????????????????????????????????????C.?x>1????????????????????????????????????D.?x<1
4.如图,一次函数 ( )的图像与正比例函数 ( )的图像相交于点 ,已知点 的横坐标为1,则关于 的不等式 的解集为(? )
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
5.已知一次函数y=kx+b中,x取不同值时,y对应的值列表如下:
x
…
-m2-1
2
3
…
y
…
-1
0
n2+1
…
则不等式kx+b>0(其中k,b,m,n为常数)的解集为( ??)
A.?x>2??????????????????????????????????B.?x>3??????????????????????????????????C.?x<2??????????????????????????????????D.?无法确定
6.同一平面直角坐标系中,一次函数 的图像与正比例函数 的图像如图所示,则关于 的方程 的解为(????? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
7.如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为(? ??)
A.?x>﹣2????????????????????????????????B.?x<﹣2????????????????????????????????C.?x>﹣5????????????????????????????????D.?x<﹣5
8.如图,直线过点A(0,2),且与直线交于点P(1,m),则不等式组的解是(???)
A.?1<<2??????????????????????????????B.?0<<2??????????????????????????????C.?0<<1??????????????????????????????D.?1<
二、填空题
9.如图,直线 与 轴交于点 ,则 时, 的取值范围是________。
10.如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是________.
11.如图,l1:y=x+1和l2:y=mx+n相交于P(a,2),则x+1≥mx+n解集为________.
12.已知关于x的不等式kx-2>0(k≠0)的解集是x>3,则直线y=-kx+2与x轴的交点是________。
13.已知 ,当 ________? 时, .
三、解答题
14.已知y1=-x+3,y2=3x-4,交点坐标是( , )当x取何值时,y1>y2?观察图像得出答案
15.如图,函数y=2x和y=﹣x+4的图象相交于点A,
(1)求点A的坐标;
(2)根据图象,直接写出不等式2x≥﹣x+4的解集.
16.为倡导绿色出行,某共享单车近期登陆徐州,根据连续骑行时长分段计费:骑行时长在2h以内(含2h)的部分,每0.5h计费1元(不足0.5h按0.5h计算); 骑行时长超出2h的部分,每小时计费4元(不足1h按1h计算).
根据此收费标准,解决下列问题:
(1)连续骑行5h,应付费多少元?
(2)若连续骑行xh(x>2且x为整数) 需付费y元,则y与x的函数表达式为________;
(3)若某人连续骑行后付费24元,求其连续骑行时长的范围.
答案解析部分
一、单选题
1.【答案】 D
解:∵直线y=kx+b交x轴于A(-2,0),
结合函数图形可知不等式kx+b>0解集对应直线在x轴上方部分图象上点的横坐标的集合;
∴不等式kx+b>0的解集是x>-2,
故答案为:D.
2.【答案】 B
解:通过观察函数图像可知要使 需要看图像在上方时候横坐标的取值范围,可以得出当x<-1时候满足条件;故答案是B选项
3.【答案】 B
解:由一次函数的图象可知,此函数是减函数,
?????????????????? ∵一次函数y=kx+b的图象与y轴交于点(0,1),
?????????????????? ∴当x<0时,关于x的不等式kx+b>1.
故选B.
4.【答案】A
解:当x<1时,kx+3>mx,所以关于x的不等式(k-m)x>-3的解集为x<1.故答案为:A.
5.【答案】 A
解:由表格可得:x=2时,y=0,由n2+1>0,
则x>2时,不等式kx+b>0(其中k,b,m,n为常数).
故答案为:A.
6.【答案】 D
解:y=k1x?2b=k1x+b?3b是由y=k1x+b向上平移?3b个单位得到的,
∵y=k1x+b与y=k2x交点的横坐标为?2,
∴y=k1x?2b与y=k2x的交点的横坐标为4,
∴方程k1x?2b>k2x的解为:x<4.
故选:D.
7.【答案】 A
解:从图像得到,当x>﹣2时,y1=3x+b的图像对应的点在函数y2=ax﹣3的图像上面,
∴不等式3x+b>ax﹣3的解集为:x>﹣2.
故答案为:A.
8.【答案】 A
解:由于一次函数y1同时经过A、P两点,可将它们的坐标分别代入y1的解析式中,即可求得k、b与m的关系,将其代入所求不等式组中,即可求得不等式的解集.
由于直线y1=kx+b过点A(0,2),P(1,m),
则有:
k+b=m
b=2
解得
k=m?2
b=2
∴直线y1=(m-2)x+2.
故所求不等式组可化为:mx>(m-2)x+2>mx-2,
解得:1<x<2.
9.【答案】
解:从图像可以观察当y大于0的时候,x的取值范围是 ,故答案是
10.【答案】x>﹣2
解:从图象得到,当x>﹣2时,y=3x+b的图象对应的点在函数y=ax﹣3的图象上面,
∴不等式3x+b>ax﹣3的解集为:x>﹣2.
故答案为:x>﹣2.
11.【答案】x≥1
解∵直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),
∴a+1=2,
解得:a=1,
观察图象知:关于x的不等式x+1≥mx+n的解集为x≥1.
12.【答案】(3,0)
解:因为不等式kx-2>0(k≠0)的解集是x>3,所以可以求得k的值是 ,将k的值代入y=-kx+2,得到y=- x+2 ,与x轴的交点是纵坐标是0,即0=- x+2,解得x=3,所以坐标是(3,0)
13.【答案】 x>-1
解:∵ ,
∴5+x>-2x+2
3x>-3
x>-1
故答案为:x>-1.
三、解答题
14.【答案】 若y1>y2 , 观察函数y1的图像在函数y2的上方,当x取小于 的值时,有y1>y2
解:若y1>y2 , 那么只需要观察函数y1的图像在函数y2的上方即可,当x取小于 的值时,有y1>y2
15.【答案】 解:(1)由, 解得:, ∴A的坐标为(, 3);(2)由图象,得不等式2x≥﹣x+4的解集为:x≥.
16.【答案】 (1)解:当x=5时,y=2×2+4×(5﹣2)=16,
∴应付16元。
(2)y=4(x﹣2)+2×2=4x﹣4;
故答案为:y=4x﹣4;
(3)当y=24,24=4x﹣4,
x=7,
∴连续骑行时长的范围是:6<x≤7
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
