湖南省岳阳市湘阴县知源学校2020-2021学年八年级上学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 湖南省岳阳市湘阴县知源学校2020-2021学年八年级上学期期末考试数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 366.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 18:24:46 | ||
图片预览


文档简介
数学试题
一、选择题(本大题共8小题,共24分)
1.下列代数式中,属于分式的是( )
A.-3 B. C. D.
2.实数,0,,0.33,,中无理数有( )个
A.1 B.2 C.3 D.4
3.4的算术平方根是( )
A. B. C. D.
4.如图,数轴表示的不等式组的解集是( )
A. B. C. D.
5.若等腰三角形的一个内角是40°,则这个等腰三角形的其他内角的度数为( )
A.40°,100° B.70°,70°
C.40°,100°或70°,70° D.以上都不对
6.如图,是用直尺和圆规作等于已知的示意图,则图中两个三角形全等的依据是( )
A. B. C. D.
7.设为实数,且,则的值是( )
A.1 B.9 C.4 D.5
8.在数轴上,点表示1,现将点沿轴做如下移动:第一次点向左移动3个单位长度到达点,第二次将点向右移动6个单位长度到达点,第三次将点向左移动9个单位长度到达点,按照这种移动规律移动下去,第次移动到点,如果点与原点的距离不小于30,那么的最小值是( )
A.19 B.20 C.21 D.22
二、填空题(本大题共6小题,共18分)
9.对于分式,当______时,分式有意义.
10.科学家发现一种病毒的直径为微米,则这种病毒的直径用科学计数法表示为________微米.
4260850190500011.4的平方根是________;的算术平方根是________;的立方根是________.
39179501187450012.如图,,要使,需添加的一个条件是_____________(只添一个条件即可).
13.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC=_____.
14.关于的方程的解为正整数,且关于的不等式组有解且最多有个整数解,则满足条件的所有整数的值为_______.
三、解答题
15.(本题共5分)解不等式:
16.(本题共5分)解方程:
17.(本题共6分)把下列命题改写成“如果…,那么…”
(1)同旁内角互补,两直线平行;
(2)a+b=0,则a与b互为相反数;
(3)平行于同一条直线的两条直线平行.
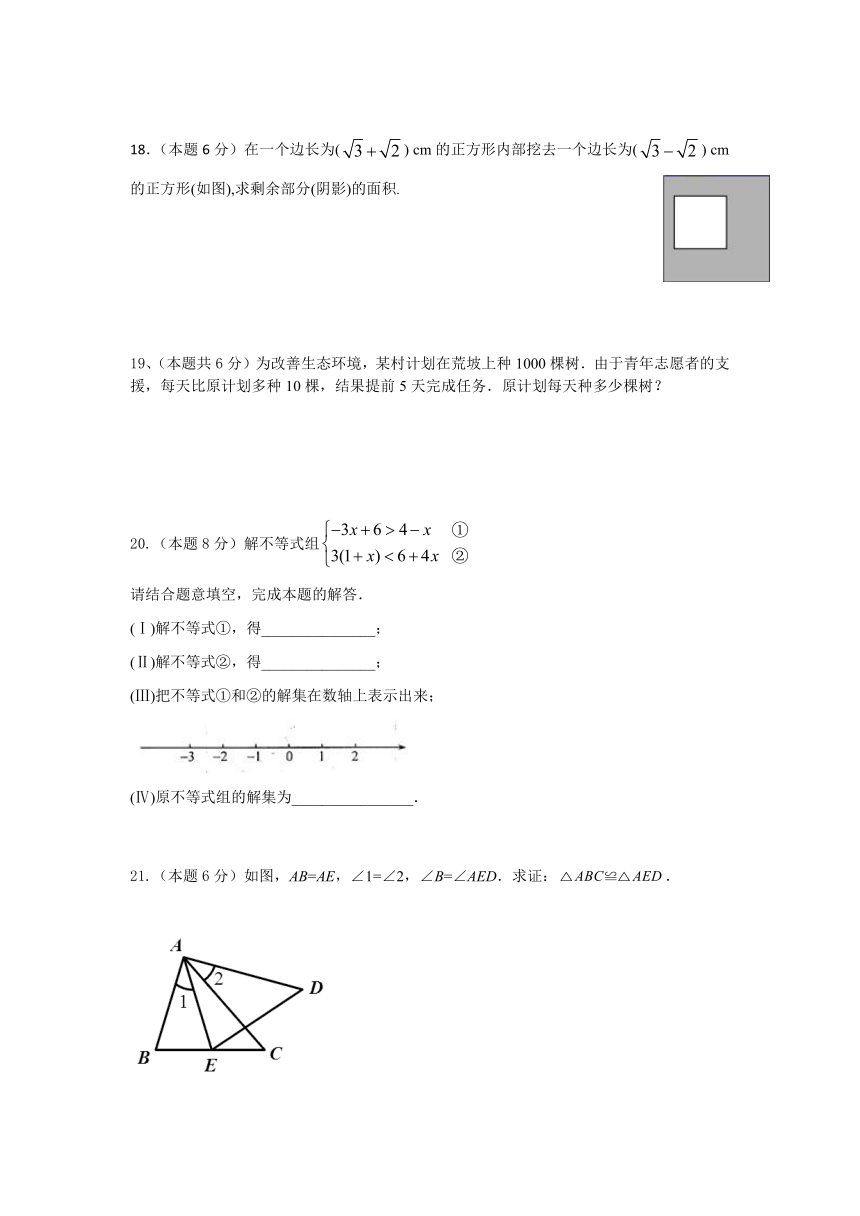
46863004279900018.(本题6分)在一个边长为() cm的正方形内部挖去一个边长为() cm的正方形(如图),求剩余部分(阴影)的面积.
19、(本题共6分)为改善生态环境,某村计划在荒坡上种1000棵树.由于青年志愿者的支援,每天比原计划多种10棵,结果提前5天完成任务.原计划每天种多少棵树?
20.(本题8分)解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为________________.
21.(本题6分)如图,AB=AE,∠1=∠2,∠B=∠AED.求证:.
22.(本题6分)为了增加同学们对新冠肺炎防控知识的了解,某班级组织了一次测验,共有15道选择题,评分标准为:答对一道题给2分,答错一道题扣2分,不答题不给分也不扣分.小强同学在答题时除了有2道题不会没有给出答案外,对其它题都给出了答案,若他想让自己的总分不低于16分,那么他至少要答对几道题?
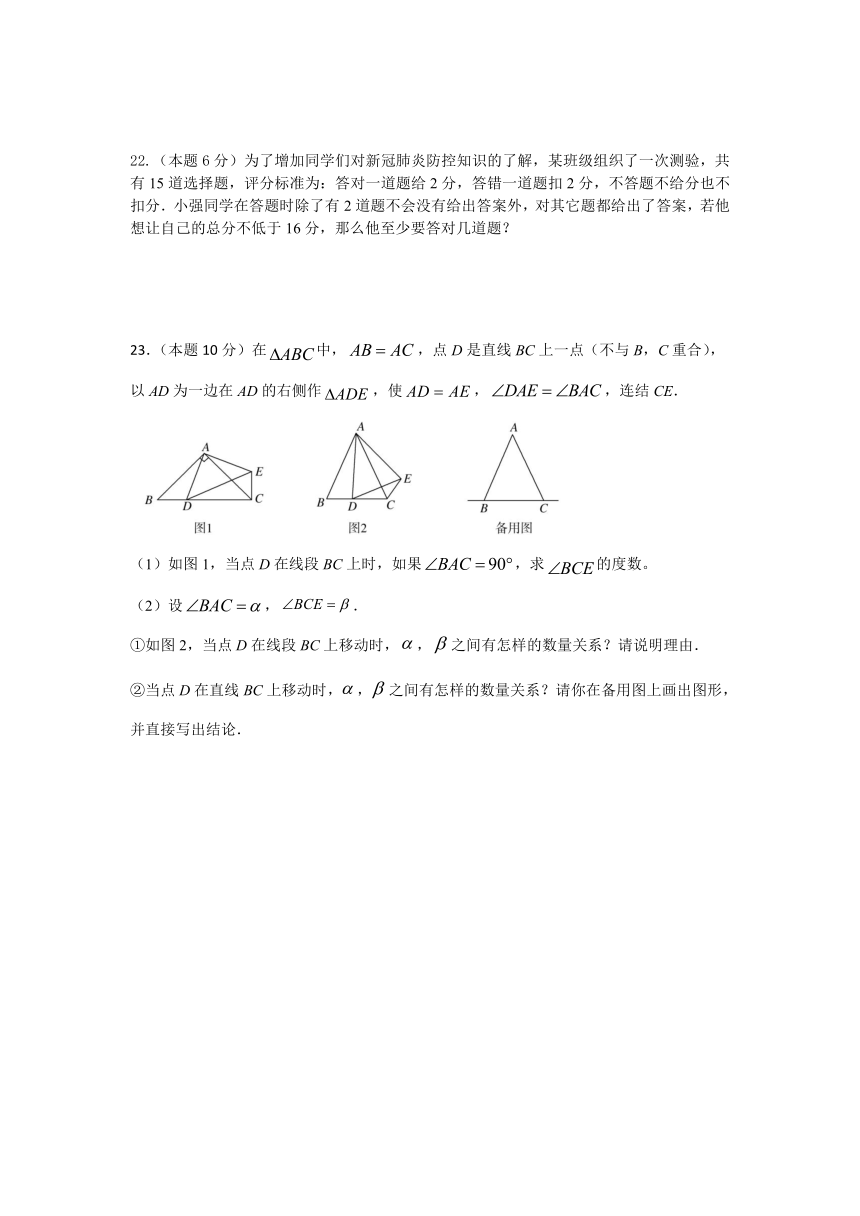
23.(本题10分)在中,,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作,使,,连结CE.
(1)如图1,当点D在线段BC上时,如果,求的度数。
(2)设,.
①如图2,当点D在线段BC上移动时,,之间有怎样的数量关系?请说明理由.
②当点D在直线BC上移动时,,之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论.
参考答案
1.C 2.B 3.C 4.A 5.C 6.A 7.A
8.B
由题意得:表示的数为
表示的数为
表示的数为
表示的数为
表示的数为
归纳类推得:每移动2次后,点与原点的距离增加3个单位长度
移动20次时,点与原点的距离为30
则n的最小值为20
故选:B.
9. 10.
11.
12.或或
13.12
14.﹣2,﹣1
解:分式方程去分母得:8﹣4x=ax﹣x,
解得:x=,
由分式方程解为正整数,得到a+3=1,2,4,8,
解得:a=﹣2,﹣1,1,5,
又∵x≠2,
∴a≠1,
∴a=﹣2,﹣1,5,
不等式组整理得:,
解得:a≤x<5,
由不等式组有解且最多有7个整数解,得到整数解为4,3,2,1,0,﹣1,﹣2,
∴﹣3<a<5,
∴整数解为4,3,2,1,0,﹣1,﹣2,
则满足题意a的值为﹣2,﹣1,
故答案为:﹣2,﹣1.
15.x>6
解:移项得:
合并同类项得:x>6.
16.x=-4
解:方程两边同乘以得
x=-4
经检验,x=-4是方程的解.
17.(1)如果同旁内角互补,那么两直线平行;
(2)如果,那么a与b互为相反数;
(3)如果两条直线平行于同一条直线,那么这两条直线平行.
18.4
试题解析:
S阴=()2-()2
=3+2+2-3+2-2
=4(cm2),
即阴影部分的面积是4 cm2.
19.原计划每天种树40棵.
解:设原计划每天种棵,根据题意得
.
,
经检验,,都是原方程的根,但不合题意,舍去
答:原计划每天种树40棵.
20.解:(Ⅰ)由①得:
故答案为:;
(Ⅱ)由②得:,
故答案为:;
(Ⅲ)把不等式①②的解集在数轴上表示如下:
(Ⅳ)根据数轴得到不等式组的解集为:
.
故答案为:.
21.证明:
在与中,
22.解:设小明答对x道题,
根据题意,可得 ,
解得,
因为 x 是整数,所以 x 最小整数值是 11 ,
答:小明至少要答对 11 道题,总分才不会低于16分.
23.(1);
证明:∵,
∴;
∴;
在和中,
,
∴;
∴;
∴;
故答案为90°;
(2)①由(1)中可知,
∴、存在的数量关系为;
证明方法同(1)中证明
②当点D在射线BC上时,如图1,
同(1)的方法即可得出,;
∴,
∴,
∴;
当点D在射线BC的反向延长线上时,如图2,
同(1)的方法即可得出,;
∴,
∴,
∴.
一、选择题(本大题共8小题,共24分)
1.下列代数式中,属于分式的是( )
A.-3 B. C. D.
2.实数,0,,0.33,,中无理数有( )个
A.1 B.2 C.3 D.4
3.4的算术平方根是( )
A. B. C. D.
4.如图,数轴表示的不等式组的解集是( )
A. B. C. D.
5.若等腰三角形的一个内角是40°,则这个等腰三角形的其他内角的度数为( )
A.40°,100° B.70°,70°
C.40°,100°或70°,70° D.以上都不对
6.如图,是用直尺和圆规作等于已知的示意图,则图中两个三角形全等的依据是( )
A. B. C. D.
7.设为实数,且,则的值是( )
A.1 B.9 C.4 D.5
8.在数轴上,点表示1,现将点沿轴做如下移动:第一次点向左移动3个单位长度到达点,第二次将点向右移动6个单位长度到达点,第三次将点向左移动9个单位长度到达点,按照这种移动规律移动下去,第次移动到点,如果点与原点的距离不小于30,那么的最小值是( )
A.19 B.20 C.21 D.22
二、填空题(本大题共6小题,共18分)
9.对于分式,当______时,分式有意义.
10.科学家发现一种病毒的直径为微米,则这种病毒的直径用科学计数法表示为________微米.
4260850190500011.4的平方根是________;的算术平方根是________;的立方根是________.
39179501187450012.如图,,要使,需添加的一个条件是_____________(只添一个条件即可).
13.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC=_____.
14.关于的方程的解为正整数,且关于的不等式组有解且最多有个整数解,则满足条件的所有整数的值为_______.
三、解答题
15.(本题共5分)解不等式:
16.(本题共5分)解方程:
17.(本题共6分)把下列命题改写成“如果…,那么…”
(1)同旁内角互补,两直线平行;
(2)a+b=0,则a与b互为相反数;
(3)平行于同一条直线的两条直线平行.
46863004279900018.(本题6分)在一个边长为() cm的正方形内部挖去一个边长为() cm的正方形(如图),求剩余部分(阴影)的面积.
19、(本题共6分)为改善生态环境,某村计划在荒坡上种1000棵树.由于青年志愿者的支援,每天比原计划多种10棵,结果提前5天完成任务.原计划每天种多少棵树?
20.(本题8分)解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为________________.
21.(本题6分)如图,AB=AE,∠1=∠2,∠B=∠AED.求证:.
22.(本题6分)为了增加同学们对新冠肺炎防控知识的了解,某班级组织了一次测验,共有15道选择题,评分标准为:答对一道题给2分,答错一道题扣2分,不答题不给分也不扣分.小强同学在答题时除了有2道题不会没有给出答案外,对其它题都给出了答案,若他想让自己的总分不低于16分,那么他至少要答对几道题?
23.(本题10分)在中,,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作,使,,连结CE.
(1)如图1,当点D在线段BC上时,如果,求的度数。
(2)设,.
①如图2,当点D在线段BC上移动时,,之间有怎样的数量关系?请说明理由.
②当点D在直线BC上移动时,,之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论.
参考答案
1.C 2.B 3.C 4.A 5.C 6.A 7.A
8.B
由题意得:表示的数为
表示的数为
表示的数为
表示的数为
表示的数为
归纳类推得:每移动2次后,点与原点的距离增加3个单位长度
移动20次时,点与原点的距离为30
则n的最小值为20
故选:B.
9. 10.
11.
12.或或
13.12
14.﹣2,﹣1
解:分式方程去分母得:8﹣4x=ax﹣x,
解得:x=,
由分式方程解为正整数,得到a+3=1,2,4,8,
解得:a=﹣2,﹣1,1,5,
又∵x≠2,
∴a≠1,
∴a=﹣2,﹣1,5,
不等式组整理得:,
解得:a≤x<5,
由不等式组有解且最多有7个整数解,得到整数解为4,3,2,1,0,﹣1,﹣2,
∴﹣3<a<5,
∴整数解为4,3,2,1,0,﹣1,﹣2,
则满足题意a的值为﹣2,﹣1,
故答案为:﹣2,﹣1.
15.x>6
解:移项得:
合并同类项得:x>6.
16.x=-4
解:方程两边同乘以得
x=-4
经检验,x=-4是方程的解.
17.(1)如果同旁内角互补,那么两直线平行;
(2)如果,那么a与b互为相反数;
(3)如果两条直线平行于同一条直线,那么这两条直线平行.
18.4
试题解析:
S阴=()2-()2
=3+2+2-3+2-2
=4(cm2),
即阴影部分的面积是4 cm2.
19.原计划每天种树40棵.
解:设原计划每天种棵,根据题意得
.
,
经检验,,都是原方程的根,但不合题意,舍去
答:原计划每天种树40棵.
20.解:(Ⅰ)由①得:
故答案为:;
(Ⅱ)由②得:,
故答案为:;
(Ⅲ)把不等式①②的解集在数轴上表示如下:
(Ⅳ)根据数轴得到不等式组的解集为:
.
故答案为:.
21.证明:
在与中,
22.解:设小明答对x道题,
根据题意,可得 ,
解得,
因为 x 是整数,所以 x 最小整数值是 11 ,
答:小明至少要答对 11 道题,总分才不会低于16分.
23.(1);
证明:∵,
∴;
∴;
在和中,
,
∴;
∴;
∴;
故答案为90°;
(2)①由(1)中可知,
∴、存在的数量关系为;
证明方法同(1)中证明
②当点D在射线BC上时,如图1,
同(1)的方法即可得出,;
∴,
∴,
∴;
当点D在射线BC的反向延长线上时,如图2,
同(1)的方法即可得出,;
∴,
∴,
∴.
同课章节目录
