人教版七年级数学 下册 第七章 7.1.2 平面直角坐标系 课件(共50张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第七章 7.1.2 平面直角坐标系 课件(共50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览






文档简介
(共50张PPT)
温故知新
1.什么是有序数对?
2.在电影院5排3号用(5,3)表示,那么6排2号可表示为_____.
3.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是(
)
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
A
B
如何确定数轴上点的位置?
1米
温故知新
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
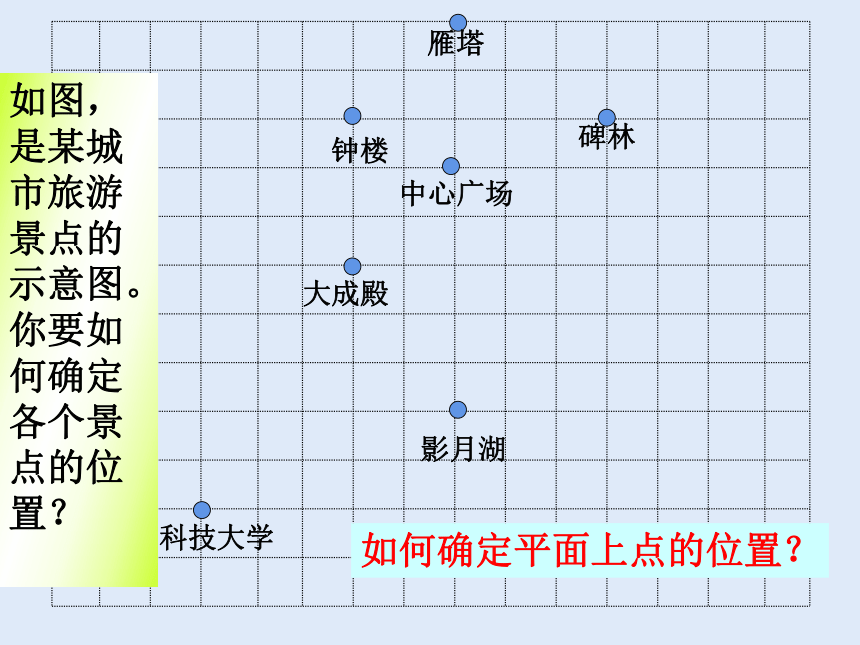
如图,是某城市旅游景点的示意图。你要如何确定各个景点的位置?
如何确定平面上点的位置?
7.1.2
平面直角坐标系
人教版七年级数学
下册
学习目标
1、认识平面直角坐标系,并能在方格纸上建立适当的平面直角坐标系。
2、了解点与坐标的对应关系。
3、在给定的直角坐标系中,已知点的位置可以写出点的坐标。
4、在平面直角坐标系中四个象限的点对应坐标的符号特征。
重点
理解平面直角坐标系的概念。
难点
象限内点对应坐标的符号特征,根据点的坐标判断其所在象限。
认真阅读课本中7.1.2
平面直角坐标系的内容,完成下面任务。
自主研学
学习任务:
1.如何确定一个点在数轴上的位置.
2.平面直角坐标系的概念,如何建立平面直角坐标系,象限划分.
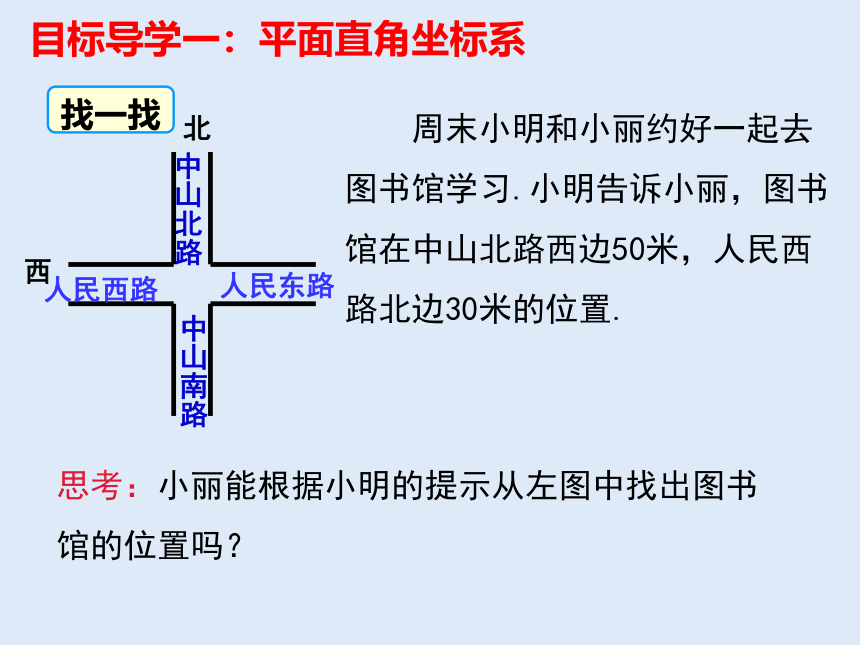
思考:小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
中山南路
人民东路
中山北路
人民西路
北
西
找一找
目标导学一:平面直角坐标系
中山南路
人民东路
中山北路
人民西路
北
西
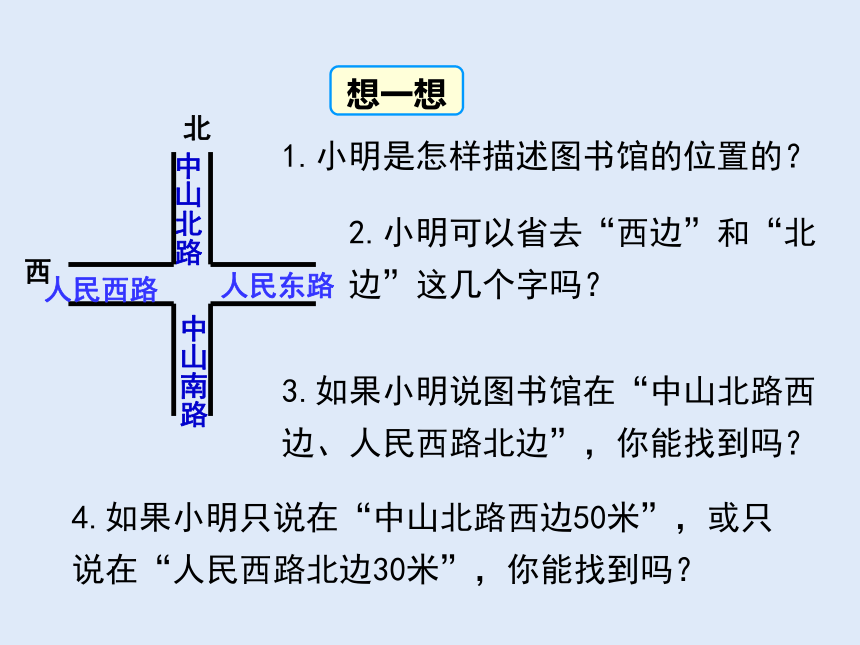
想一想
4.如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
1.小明是怎样描述图书馆的位置的?
2.小明可以省去“西边”和“北边”这几个字吗?
3.如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
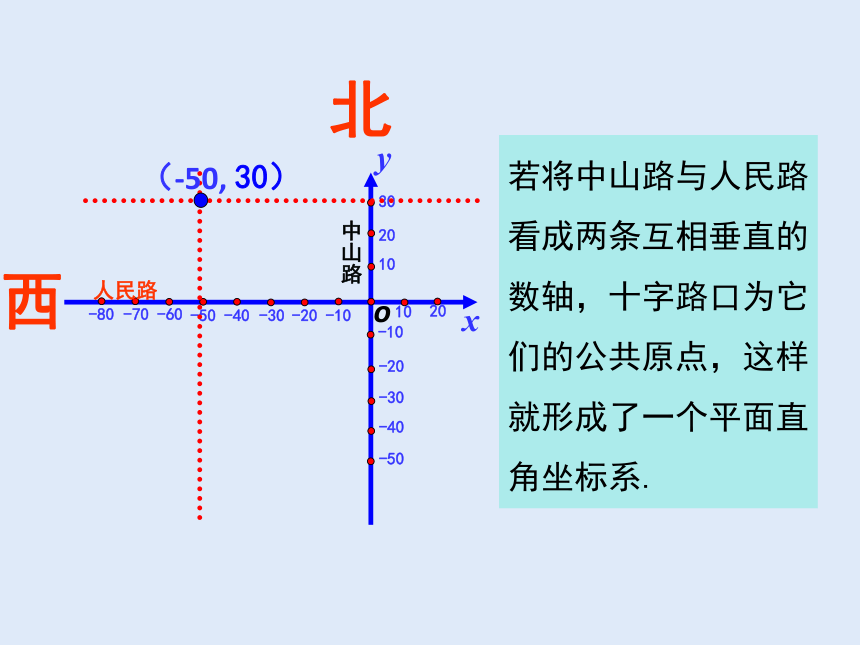
若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
法国数学家笛卡尔(Descartes,
1596一1650),最早引入坐标系,
用代数方法研究几何图形.
1
2
3
-1
-2
-3
O
1
-1
2
-2
-3
3
x
y
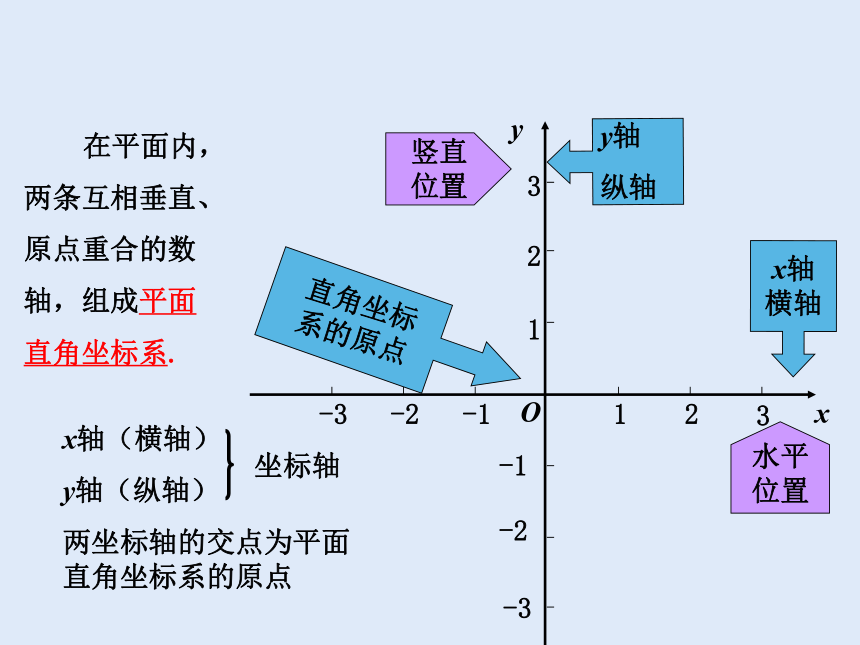
x轴
横轴
y轴
纵轴
直角坐标
系的原点
在平面内,两条互相垂直、原点重合的数轴,组成平面直角坐标系.
水平
位置
竖直
位置
x轴(横轴)
y轴(纵轴)
两坐标轴的交点为平面直角坐标系的原点
坐标轴
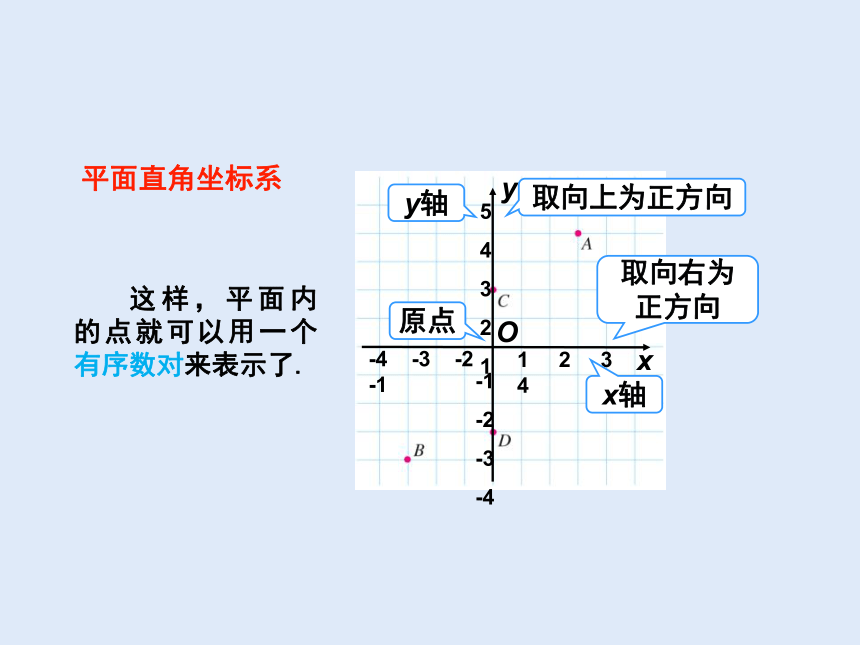
这样,平面内的点就可以用一个有序数对来表示了.
x
y
O
1
2
3
4
5
4
3
2
1
-4
-3
-2
-1
-1
-2
-3
-4
x轴
y轴
原点
平面直角坐标系
取向右为正方向
取向上为正方向
平面直角坐标系中两坐标轴的特征:
①互相垂直;
②原点重合;
③通常取向上、向右为正方向;
④单位长度一般取相同的,在有些实际问题中,两坐标轴上的单位长度可以不同.
x
O
下面四个图形中,是平面直角坐标系的是(
)
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3
2
1
-1
-2
-3
x
y
(B)
2
1
-1
-2
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
(C)
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
y
(D)
O
D
点的坐标
x
y
O
1
2
3
4
5
4
3
2
1
-4
-3
-2
-1
-1
-2
-3
-4
(
,
)
3
4
(
,
)
-3
-4
横坐标
纵坐标
原点的坐标是?
x轴和y轴上的点的坐标有什么特点?
判断点的坐标
尝试用有序数对表示点A,B,C,D的位置。
A(_____,_____)
B(_____,_____)
C(_____,_____)
D(_____,_____)
A
B
C
D
y
x
0
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
5
5
8
2
2
6
8
4
我们说
A点的横坐标是5,
纵坐标是8,
有序数对(5,
8)就叫做A点的坐标,
记作
A(5,
8)
由点A分别向x轴、y轴作垂线,
垂足M
在x轴上的坐标5,
垂足N在y轴上的坐标是8.
M
N
即学即练
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
例:在平面直角坐标系中
找点A(3,-2)
由坐标找点的方法:
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
例:已知坐标平面内的点,说出它的坐标.
如图:说出A,B,C,D,M,N各点的坐标.
-4
–3
–2
–1
O
1
2
3
4
5
-1
-2
-3
-4
x
y
●
●
1
2
3
4
●
●
●
●
A
(3,4)
B
C
D
N
M
(-3,-4)
(0,2)
(0,-3)
(3,0)
(0,4)
如图,在平面直角坐标系中写出图中点A,B,C,D,E
的坐标.
答:
A(-2,-2),
B(-5,4),
C(5,-4),
D(0,-3),
E(3,5).
即学即练
我们知道,数轴上的点与实数是一一对应的.我们还可以得出:对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)(即点M的坐标)和它对应;
反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.也就是说,坐标平面内的点与有序实数对是一一对应的.
知识归纳
原点O的坐标是什么?x轴和y轴上的点坐标有什么特点?
A
B
C
D
点
A
B
O
C
D
坐标
(
2,0
)
(
-3,0
)
(
0,0
)
(
0,4
)
(
0,-6
)
1.
x轴上的点,纵坐标等于0;
2.
y轴上的点,横坐标等于0;
3.
原点位置的点,横、纵坐标都为0.
目标导学二:直角坐标系中点的坐标的特征
y
O
-6
-5
-4
-3
-2
-1
5
4
3
2
1
-1
-2
-3
-4
-5
x
1
2
3
4
5
6
平面直角坐标系将平面分成四个象限
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
1
2
3
-1
-2
-3
O
1
-1
2
-2
-3
3
x
y
a
b
对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标.
记作:P(a,b)
温馨提示:横坐标必须写在纵坐标前面
根据点的坐标找对应位置
解:
如图,
先在x轴上找出表示4的点,
再在y轴上找出表示5的点,
过这两个点分别作x轴和y轴的垂线,
垂线的交点就是点A.
在平面直角坐标系中描出下列各点
A(4,
5)
,
B(-2,
3),
C(-4,
-1),D(2.5,
-2),
E(0,
-4)
A
尝试画出其它点的坐标,
观察这些坐标,你发现它们所在象限
与点的坐标之间有什么关系?
即学即练
活动:
观察坐标系,填写各象限内的点的坐标的特征:
点的位置
横坐标的符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5)
,
B(-2,3),
C(-4,
-1),
D(2.5,-2),
E(0,-4)所在的象限吗?你的方法又是什么?
点的位置
横坐标的符号
纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),
C(-4,0),E(0,-4),O(0,0)所在的位置吗?你的方法又是什么?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动.观察坐标系,填写坐标轴上的点的坐标的特征:
在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限或哪条坐标轴上:
(1)点P(x,y)的坐标满足xy>0;
(2)点P(x,y)的坐标满足xy<0;
(3)点P(x,y)的坐标满足xy=0;
(4)点P(x,y)的坐标满足x2+y2=0.
第一、三象限
第二、四象限
在任意一条坐标轴上
在原点处
即学即练
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或y轴负半轴上(a=0,b<0).
例
已知a那么点P(a,-b)在第
象限.
二
【方法总结】求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求出相应字母的取值范围.
即学即练
若设点M(a,b),
M点关于X轴的对称点M1(
)
M点关于Y轴的对称点M2(
)
M点关于原点O的对称点M3(
)
a,-b
-
a,
b
-a,-b
即学即练
例:若点A(-2,n)在x轴上,则点B(n-2,n+1)在
(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
分析:∵点A(-2,n)在x轴上,∴n=0,
∴B为(-2,1)
∴点B在第二象限。
B
已知点
A(2,n),
B(m,-4)不重合,若线段
AB//y轴,且
A,B到x轴的距离相等,则m=______,n=________。
4
2
即学即练
本类题的易错点有三处:
①混淆距离与坐标之间的区别;
②不知道“点P到x轴的距离”对应的是纵坐标,“点P到y轴的距离”对应的是横坐标;
③忽略坐标的符号出现错解.若本例题只已知距离而无附加条件,则点P的坐标有四个.
方法归纳
问题:正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
目标导学三:建立坐标系求图形中点的坐标
4
4
y
x
(A)
B
C
D
解:如图,以顶点A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.
此时,正方形四个顶点A,B,C,D的坐标分别为:
A(0,0),
B(4,0),
C(4,4),
D(0,4).
O
A
B
C
D
A(0,-4),
B(4,-4),C(4,0),
D(0,0).
y
x
O
想一想:还可以建立其他平面直角坐标系,表示正方形的四个顶点A,B,C,D的坐标吗?
A(-4,0),
B(0,0),C(0,4),
D(-4,4).
A(-4,-4),
B(0,-4),C(0,0),
D(-4,0).
A(-2,-2),
B(2,-2),C(2,2),
D(-2,2).
建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
知识归纳
探究
如图,正方形ABCD的边长为6,如果以点A为原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A,B,C,D的坐标.
x
(A)
B
C
D
O
方法总结:由已知条件正确确定坐标轴的位置是解决本题的关键.
x
y
0
.A(2,1)
.B(2,-1)
.C(-2,1)
E(3,0)
D(0,1)
.F(-2,-1)
1
-1
1、平面直角坐标系概念
2、直角坐标系中点的坐标.
3、x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4.当两点的横坐标相同,纵坐标互为相反数时,这两点关于X轴对称;当两点的纵坐标相同,横坐标互为相反数时,这两点关于Y轴对称;当两点的横坐标、纵坐标互为相反数时,这两点关于原点对称;
课堂小结
1.在平面直角坐标系的第二象限内有一点,点到轴的距离为3,到轴的距离为4,则点的坐标是(
)
A.
B.
C.
D.
【答案】C
【解析】
由题意,得x=-4,y=3,即M点的坐标是(-4,3),故选C.
检测目标
2.下列说法错误的是(
)
A
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限
检测目标
3.下列说法错误的是(
)
分析:A错误,没有明确两条数轴原点重合。
B正确。
C正确。
D正确。
A
检测目标
4.下列各点中,位于第四象限的是( )
A.(4,3)
B.(﹣3,5)
C.(3,﹣4)
D.(﹣4,﹣3)
检测目标
5.
在平面直角坐标系中,若A(-3,-2),则点A到x轴的距离为(
)
D
A.-3
B.3
C.-2
D.2
检测目标
检测目标
6.实数
x,y满足
(x-1)2+
|y|
=
0,则点
P(
x,y)在(
)
(A)原点
(B)x轴正半轴
(C)第一象限
(D)任意位置
B
7.写出图中点A,B,C,D,E,F的坐标.
(-2,-2)
(-5,4)
(5,-4)
(2,5)
(-3,0)
(0,-3)
检测目标
8.在平面直角坐标系中描出下列各点:
A(4,5),
B(-2,3),
C(-4,-1),
D(2.5,-2),
E(0,-4).
-4
–3
–2
–1
O
1
2
3
4
5
-1
-2
-3
-4
x
y
●
1
2
3
4
5
A(4,5)
●
B(-2,3)
●
C(-4,-1)
●
D(2.5,-2)
●
E(0,-4)
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
温故知新
1.什么是有序数对?
2.在电影院5排3号用(5,3)表示,那么6排2号可表示为_____.
3.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是(
)
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
A
B
如何确定数轴上点的位置?
1米
温故知新
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
如图,是某城市旅游景点的示意图。你要如何确定各个景点的位置?
如何确定平面上点的位置?
7.1.2
平面直角坐标系
人教版七年级数学
下册
学习目标
1、认识平面直角坐标系,并能在方格纸上建立适当的平面直角坐标系。
2、了解点与坐标的对应关系。
3、在给定的直角坐标系中,已知点的位置可以写出点的坐标。
4、在平面直角坐标系中四个象限的点对应坐标的符号特征。
重点
理解平面直角坐标系的概念。
难点
象限内点对应坐标的符号特征,根据点的坐标判断其所在象限。
认真阅读课本中7.1.2
平面直角坐标系的内容,完成下面任务。
自主研学
学习任务:
1.如何确定一个点在数轴上的位置.
2.平面直角坐标系的概念,如何建立平面直角坐标系,象限划分.
思考:小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
中山南路
人民东路
中山北路
人民西路
北
西
找一找
目标导学一:平面直角坐标系
中山南路
人民东路
中山北路
人民西路
北
西
想一想
4.如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
1.小明是怎样描述图书馆的位置的?
2.小明可以省去“西边”和“北边”这几个字吗?
3.如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
法国数学家笛卡尔(Descartes,
1596一1650),最早引入坐标系,
用代数方法研究几何图形.
1
2
3
-1
-2
-3
O
1
-1
2
-2
-3
3
x
y
x轴
横轴
y轴
纵轴
直角坐标
系的原点
在平面内,两条互相垂直、原点重合的数轴,组成平面直角坐标系.
水平
位置
竖直
位置
x轴(横轴)
y轴(纵轴)
两坐标轴的交点为平面直角坐标系的原点
坐标轴
这样,平面内的点就可以用一个有序数对来表示了.
x
y
O
1
2
3
4
5
4
3
2
1
-4
-3
-2
-1
-1
-2
-3
-4
x轴
y轴
原点
平面直角坐标系
取向右为正方向
取向上为正方向
平面直角坐标系中两坐标轴的特征:
①互相垂直;
②原点重合;
③通常取向上、向右为正方向;
④单位长度一般取相同的,在有些实际问题中,两坐标轴上的单位长度可以不同.
x
O
下面四个图形中,是平面直角坐标系的是(
)
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3
2
1
-1
-2
-3
x
y
(B)
2
1
-1
-2
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
(C)
O
-3
-2
-1
1
2
3
3
2
1
-1
-2
-3
y
(D)
O
D
点的坐标
x
y
O
1
2
3
4
5
4
3
2
1
-4
-3
-2
-1
-1
-2
-3
-4
(
,
)
3
4
(
,
)
-3
-4
横坐标
纵坐标
原点的坐标是?
x轴和y轴上的点的坐标有什么特点?
判断点的坐标
尝试用有序数对表示点A,B,C,D的位置。
A(_____,_____)
B(_____,_____)
C(_____,_____)
D(_____,_____)
A
B
C
D
y
x
0
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
5
5
8
2
2
6
8
4
我们说
A点的横坐标是5,
纵坐标是8,
有序数对(5,
8)就叫做A点的坐标,
记作
A(5,
8)
由点A分别向x轴、y轴作垂线,
垂足M
在x轴上的坐标5,
垂足N在y轴上的坐标是8.
M
N
即学即练
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
例:在平面直角坐标系中
找点A(3,-2)
由坐标找点的方法:
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
例:已知坐标平面内的点,说出它的坐标.
如图:说出A,B,C,D,M,N各点的坐标.
-4
–3
–2
–1
O
1
2
3
4
5
-1
-2
-3
-4
x
y
●
●
1
2
3
4
●
●
●
●
A
(3,4)
B
C
D
N
M
(-3,-4)
(0,2)
(0,-3)
(3,0)
(0,4)
如图,在平面直角坐标系中写出图中点A,B,C,D,E
的坐标.
答:
A(-2,-2),
B(-5,4),
C(5,-4),
D(0,-3),
E(3,5).
即学即练
我们知道,数轴上的点与实数是一一对应的.我们还可以得出:对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)(即点M的坐标)和它对应;
反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.也就是说,坐标平面内的点与有序实数对是一一对应的.
知识归纳
原点O的坐标是什么?x轴和y轴上的点坐标有什么特点?
A
B
C
D
点
A
B
O
C
D
坐标
(
2,0
)
(
-3,0
)
(
0,0
)
(
0,4
)
(
0,-6
)
1.
x轴上的点,纵坐标等于0;
2.
y轴上的点,横坐标等于0;
3.
原点位置的点,横、纵坐标都为0.
目标导学二:直角坐标系中点的坐标的特征
y
O
-6
-5
-4
-3
-2
-1
5
4
3
2
1
-1
-2
-3
-4
-5
x
1
2
3
4
5
6
平面直角坐标系将平面分成四个象限
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
1
2
3
-1
-2
-3
O
1
-1
2
-2
-3
3
x
y
a
b
对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标.
记作:P(a,b)
温馨提示:横坐标必须写在纵坐标前面
根据点的坐标找对应位置
解:
如图,
先在x轴上找出表示4的点,
再在y轴上找出表示5的点,
过这两个点分别作x轴和y轴的垂线,
垂线的交点就是点A.
在平面直角坐标系中描出下列各点
A(4,
5)
,
B(-2,
3),
C(-4,
-1),D(2.5,
-2),
E(0,
-4)
A
尝试画出其它点的坐标,
观察这些坐标,你发现它们所在象限
与点的坐标之间有什么关系?
即学即练
活动:
观察坐标系,填写各象限内的点的坐标的特征:
点的位置
横坐标的符号
纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5)
,
B(-2,3),
C(-4,
-1),
D(2.5,-2),
E(0,-4)所在的象限吗?你的方法又是什么?
点的位置
横坐标的符号
纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),
C(-4,0),E(0,-4),O(0,0)所在的位置吗?你的方法又是什么?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动.观察坐标系,填写坐标轴上的点的坐标的特征:
在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限或哪条坐标轴上:
(1)点P(x,y)的坐标满足xy>0;
(2)点P(x,y)的坐标满足xy<0;
(3)点P(x,y)的坐标满足xy=0;
(4)点P(x,y)的坐标满足x2+y2=0.
第一、三象限
第二、四象限
在任意一条坐标轴上
在原点处
即学即练
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或y轴负半轴上(a=0,b<0).
例
已知a
象限.
二
【方法总结】求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求出相应字母的取值范围.
即学即练
若设点M(a,b),
M点关于X轴的对称点M1(
)
M点关于Y轴的对称点M2(
)
M点关于原点O的对称点M3(
)
a,-b
-
a,
b
-a,-b
即学即练
例:若点A(-2,n)在x轴上,则点B(n-2,n+1)在
(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
分析:∵点A(-2,n)在x轴上,∴n=0,
∴B为(-2,1)
∴点B在第二象限。
B
已知点
A(2,n),
B(m,-4)不重合,若线段
AB//y轴,且
A,B到x轴的距离相等,则m=______,n=________。
4
2
即学即练
本类题的易错点有三处:
①混淆距离与坐标之间的区别;
②不知道“点P到x轴的距离”对应的是纵坐标,“点P到y轴的距离”对应的是横坐标;
③忽略坐标的符号出现错解.若本例题只已知距离而无附加条件,则点P的坐标有四个.
方法归纳
问题:正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
目标导学三:建立坐标系求图形中点的坐标
4
4
y
x
(A)
B
C
D
解:如图,以顶点A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系.
此时,正方形四个顶点A,B,C,D的坐标分别为:
A(0,0),
B(4,0),
C(4,4),
D(0,4).
O
A
B
C
D
A(0,-4),
B(4,-4),C(4,0),
D(0,0).
y
x
O
想一想:还可以建立其他平面直角坐标系,表示正方形的四个顶点A,B,C,D的坐标吗?
A(-4,0),
B(0,0),C(0,4),
D(-4,4).
A(-4,-4),
B(0,-4),C(0,0),
D(-4,0).
A(-2,-2),
B(2,-2),C(2,2),
D(-2,2).
建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
知识归纳
探究
如图,正方形ABCD的边长为6,如果以点A为原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A,B,C,D的坐标.
x
(A)
B
C
D
O
方法总结:由已知条件正确确定坐标轴的位置是解决本题的关键.
x
y
0
.A(2,1)
.B(2,-1)
.C(-2,1)
E(3,0)
D(0,1)
.F(-2,-1)
1
-1
1、平面直角坐标系概念
2、直角坐标系中点的坐标.
3、x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
4.当两点的横坐标相同,纵坐标互为相反数时,这两点关于X轴对称;当两点的纵坐标相同,横坐标互为相反数时,这两点关于Y轴对称;当两点的横坐标、纵坐标互为相反数时,这两点关于原点对称;
课堂小结
1.在平面直角坐标系的第二象限内有一点,点到轴的距离为3,到轴的距离为4,则点的坐标是(
)
A.
B.
C.
D.
【答案】C
【解析】
由题意,得x=-4,y=3,即M点的坐标是(-4,3),故选C.
检测目标
2.下列说法错误的是(
)
A
A.平面内两条互相垂直的数轴就构成了平面直角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每个部分称为象限
D.坐标轴上的点不属于任何象限
检测目标
3.下列说法错误的是(
)
分析:A错误,没有明确两条数轴原点重合。
B正确。
C正确。
D正确。
A
检测目标
4.下列各点中,位于第四象限的是( )
A.(4,3)
B.(﹣3,5)
C.(3,﹣4)
D.(﹣4,﹣3)
检测目标
5.
在平面直角坐标系中,若A(-3,-2),则点A到x轴的距离为(
)
D
A.-3
B.3
C.-2
D.2
检测目标
检测目标
6.实数
x,y满足
(x-1)2+
|y|
=
0,则点
P(
x,y)在(
)
(A)原点
(B)x轴正半轴
(C)第一象限
(D)任意位置
B
7.写出图中点A,B,C,D,E,F的坐标.
(-2,-2)
(-5,4)
(5,-4)
(2,5)
(-3,0)
(0,-3)
检测目标
8.在平面直角坐标系中描出下列各点:
A(4,5),
B(-2,3),
C(-4,-1),
D(2.5,-2),
E(0,-4).
-4
–3
–2
–1
O
1
2
3
4
5
-1
-2
-3
-4
x
y
●
1
2
3
4
5
A(4,5)
●
B(-2,3)
●
C(-4,-1)
●
D(2.5,-2)
●
E(0,-4)
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
