2.4.1 二次函数的应用 课件(共21张PPT)
文档属性
| 名称 | 2.4.1 二次函数的应用 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 22:26:45 | ||
图片预览






文档简介
第4节 二次函数的应用
(第1课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.
2.学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.
学习目标
想一想:如何求出二次函数 y = ax2 + bx + c 的最小(大)值?
由于抛物线y = ax 2 + bx + c 的顶点是最低(高)点,当 时,二次函数 y = ax 2 + bx + c 有最小(大) 值
当自变量的取值范围是全体实数时,
(1)若a>0时,在顶点处取得最小值,此时不存在最大值;
a<0时,在顶点处取得最大值,此时不存在最小值.
新课导入
当自变量的取值范围是x1≤x≤x2时,
(1)若 在自变量的取值范围x1≤x≤x2内,
最大值与最小值同时存在,
如图①,当a>0时, 最小值在x= 处取得,
最大值为函数在x=x1,x=x2时的较大的函数值;
当a<0时,最大值在x= 处取得,
最小值为函数在x=x1,x=x2时的较小的函数值;
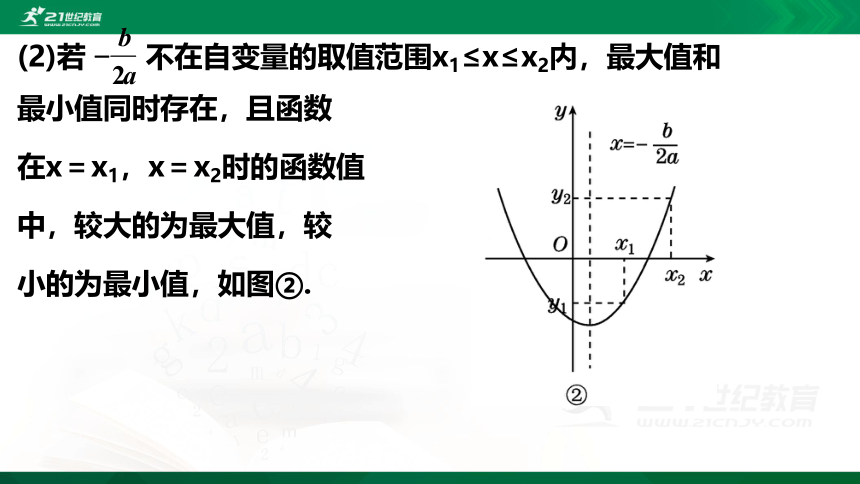
(2)若 不在自变量的取值范围x1≤x≤x2内,最大值和最小值同时存在,且函数
在x=x1,x=x2时的函数值
中,较大的为最大值,较
小的为最小值,如图②.
二次函数的最值
知识点一
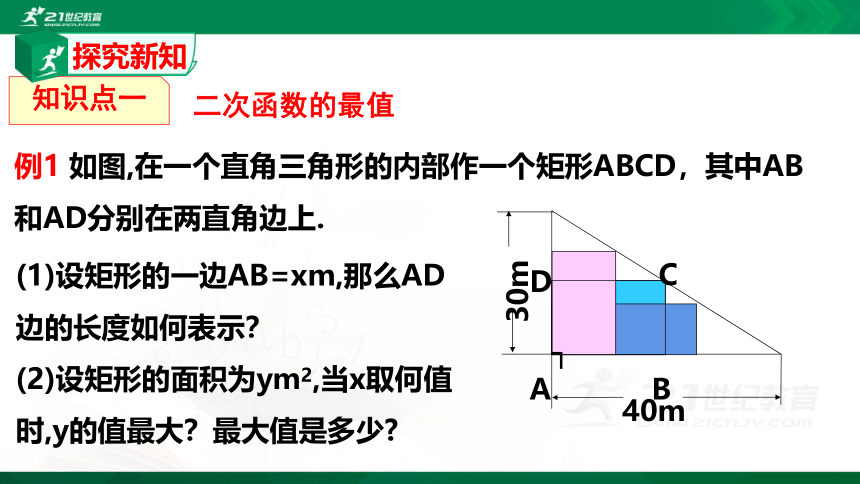
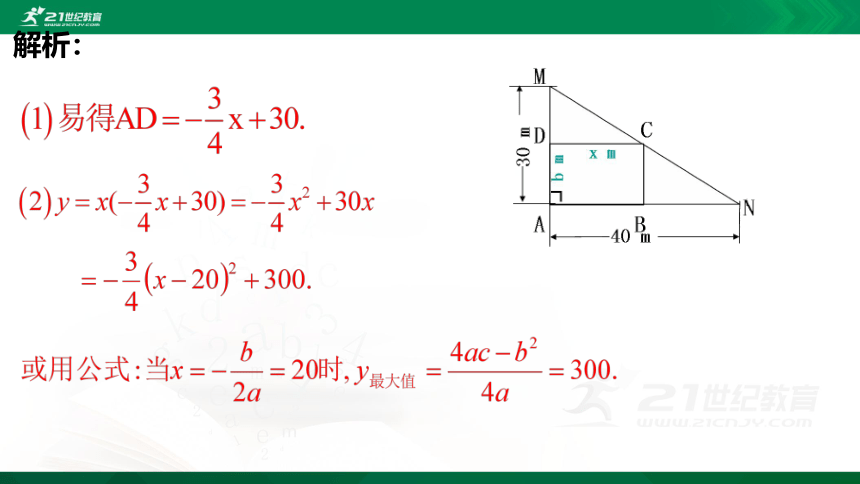
(1)设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少?
例1 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
40m
30m
A
B
C
D
┐
探究新知
解析:
总结:1.利用二次函数求几何图形的面积的最值的一般步骤:
(1)引入自变量;
(2)用含有自变量的代数式分别表示与所求几何图形相关的量;
(3)由几何图形的特征,列出其面积的计算公式,并且用函数表示这个面积;
(4)根据函数的关系式及自变量的取值范围求出其最值.
例2 分别在下列范围内求函数y=x2-2x-3的最值:
(1)0<x<2;(2)2≤x≤3.
解:∵y=x2-2x-3=(x-1)2-4,
∴图象的顶点坐标为(1,-4).
(1)∵x=1在0<x<2范围内,且a=1>0,
∴当x=1时,y有最小值,y最小值=-4.
∵x=1是0<x<2范围的中点,在直线x=1两侧的图象左右对称,端点处取不到, ∴不存在最大值.
例题讲解
(2)∵x=1不在2≤x≤3范围内(如图),而函数y=x2-2x-3(2≤x≤3)的图象是抛物线y=x2-2x-3的一部分,且当2≤x≤3时,y随x的增大而增大,
∴当x=3时,
y最大值=32-2×3-3=0;
当x=2时,
y最小值=22-2×2-3=-3.
例3 某建筑物的窗户如图,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15 m,当x等于多少时,窗户通过的光线最多?(结果精确到0.01 m)此时,窗户的面积是多少?(结果精确到0.01 m2)
x
x
y
解: ∵ 7x+4y+πx=15,
设窗户的面积是Sm2,则S= πx2+2xy
当x= ≈1.07 时,S最大 = ≈4.02.
因此,当x约为1.07m时,窗户通过的光线最多.
此时,窗户的面积约为 4.02 m2.
例4 〈实际应用题,易错题〉张大伯准备用一面长15 m的墙和长38m的栅栏修建一个如图所示的矩形养殖场ABCD,并在养殖场的一侧留出一个2 m宽的门.
(1)求养殖场的面积y(m2)与BC边的长x(m)之间的函数关系式.
(2)当BC边的长为多少时,养殖场的面积最大?最大面积是多少?
解:(1)由题意得,AB= m,
∴y=x· =x· =- x2+20x.
由题意知
∴0<x≤15.∴y=- x2+20x,其中0<x≤15.
(2)y=- x2+20x=- (x2-40x)
=- (x-20)2+200.
∵a=- <0,0<x≤15,∴y随x的增大而增大.
∴当x=15时,y最大=- ×(15-20)2+200=187.5.
答:BC边的长为15 m时,养殖场的面积最大,最大面
积是187.5 m2.
1 二次函数y=x2-4x+c的最小值为0,则c的值为( )
A.2 B.4 C.-4 D.16
课堂练习
2 已知0≤x≤ ,那么函数y=-2x2+8x-6的最大值是( )
A.-6 B.-2.5
C.2 D.不能确定
3 已知一个直角三角形两直角边长之和为20 cm,则
这个直角三角形的最大面积为( )
A.25 cm2 B.50 cm2
C.100 cm2 D.不确定
4 用一条长为40 cm的绳子围成一个面积为a cm2的长
方形,a的值不可能为( )
A.20 B.40 C.100 D.120
5 如果把矩形ABCD改为如图所示的位置,其他条件不变,则矩形ABCD的最大面积是多少?
A
B
C
D
E
F
G
6 如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A开始沿AB向B以2 cm/s的速度移动,点Q从点B开始沿BC向C以1 cm/s的速度移动.如果P,Q分别从A,B同时出发,当△PBQ的面积最大时,运动时间为________.
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
(二次函数的图象和性质)
实际问题
数学模型
转化
回归
(实物中的抛物线形问题)
课堂小结
(第1课时)
第二章 二次函数
2020-2021北师大版九年级数学下册
1.掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.
2.学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.
学习目标
想一想:如何求出二次函数 y = ax2 + bx + c 的最小(大)值?
由于抛物线y = ax 2 + bx + c 的顶点是最低(高)点,当 时,二次函数 y = ax 2 + bx + c 有最小(大) 值
当自变量的取值范围是全体实数时,
(1)若a>0时,在顶点处取得最小值,此时不存在最大值;
a<0时,在顶点处取得最大值,此时不存在最小值.
新课导入
当自变量的取值范围是x1≤x≤x2时,
(1)若 在自变量的取值范围x1≤x≤x2内,
最大值与最小值同时存在,
如图①,当a>0时, 最小值在x= 处取得,
最大值为函数在x=x1,x=x2时的较大的函数值;
当a<0时,最大值在x= 处取得,
最小值为函数在x=x1,x=x2时的较小的函数值;
(2)若 不在自变量的取值范围x1≤x≤x2内,最大值和最小值同时存在,且函数
在x=x1,x=x2时的函数值
中,较大的为最大值,较
小的为最小值,如图②.
二次函数的最值
知识点一
(1)设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少?
例1 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
40m
30m
A
B
C
D
┐
探究新知
解析:
总结:1.利用二次函数求几何图形的面积的最值的一般步骤:
(1)引入自变量;
(2)用含有自变量的代数式分别表示与所求几何图形相关的量;
(3)由几何图形的特征,列出其面积的计算公式,并且用函数表示这个面积;
(4)根据函数的关系式及自变量的取值范围求出其最值.
例2 分别在下列范围内求函数y=x2-2x-3的最值:
(1)0<x<2;(2)2≤x≤3.
解:∵y=x2-2x-3=(x-1)2-4,
∴图象的顶点坐标为(1,-4).
(1)∵x=1在0<x<2范围内,且a=1>0,
∴当x=1时,y有最小值,y最小值=-4.
∵x=1是0<x<2范围的中点,在直线x=1两侧的图象左右对称,端点处取不到, ∴不存在最大值.
例题讲解
(2)∵x=1不在2≤x≤3范围内(如图),而函数y=x2-2x-3(2≤x≤3)的图象是抛物线y=x2-2x-3的一部分,且当2≤x≤3时,y随x的增大而增大,
∴当x=3时,
y最大值=32-2×3-3=0;
当x=2时,
y最小值=22-2×2-3=-3.
例3 某建筑物的窗户如图,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15 m,当x等于多少时,窗户通过的光线最多?(结果精确到0.01 m)此时,窗户的面积是多少?(结果精确到0.01 m2)
x
x
y
解: ∵ 7x+4y+πx=15,
设窗户的面积是Sm2,则S= πx2+2xy
当x= ≈1.07 时,S最大 = ≈4.02.
因此,当x约为1.07m时,窗户通过的光线最多.
此时,窗户的面积约为 4.02 m2.
例4 〈实际应用题,易错题〉张大伯准备用一面长15 m的墙和长38m的栅栏修建一个如图所示的矩形养殖场ABCD,并在养殖场的一侧留出一个2 m宽的门.
(1)求养殖场的面积y(m2)与BC边的长x(m)之间的函数关系式.
(2)当BC边的长为多少时,养殖场的面积最大?最大面积是多少?
解:(1)由题意得,AB= m,
∴y=x· =x· =- x2+20x.
由题意知
∴0<x≤15.∴y=- x2+20x,其中0<x≤15.
(2)y=- x2+20x=- (x2-40x)
=- (x-20)2+200.
∵a=- <0,0<x≤15,∴y随x的增大而增大.
∴当x=15时,y最大=- ×(15-20)2+200=187.5.
答:BC边的长为15 m时,养殖场的面积最大,最大面
积是187.5 m2.
1 二次函数y=x2-4x+c的最小值为0,则c的值为( )
A.2 B.4 C.-4 D.16
课堂练习
2 已知0≤x≤ ,那么函数y=-2x2+8x-6的最大值是( )
A.-6 B.-2.5
C.2 D.不能确定
3 已知一个直角三角形两直角边长之和为20 cm,则
这个直角三角形的最大面积为( )
A.25 cm2 B.50 cm2
C.100 cm2 D.不确定
4 用一条长为40 cm的绳子围成一个面积为a cm2的长
方形,a的值不可能为( )
A.20 B.40 C.100 D.120
5 如果把矩形ABCD改为如图所示的位置,其他条件不变,则矩形ABCD的最大面积是多少?
A
B
C
D
E
F
G
6 如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A开始沿AB向B以2 cm/s的速度移动,点Q从点B开始沿BC向C以1 cm/s的速度移动.如果P,Q分别从A,B同时出发,当△PBQ的面积最大时,运动时间为________.
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
(二次函数的图象和性质)
实际问题
数学模型
转化
回归
(实物中的抛物线形问题)
课堂小结
