人教版 九年级下册 第二十七章 相似 课时训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级下册 第二十七章 相似 课时训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 587.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-02 20:32:04 | ||
图片预览


文档简介
人教版 九年级下册 第27章 相似 课时训练
一、选择题
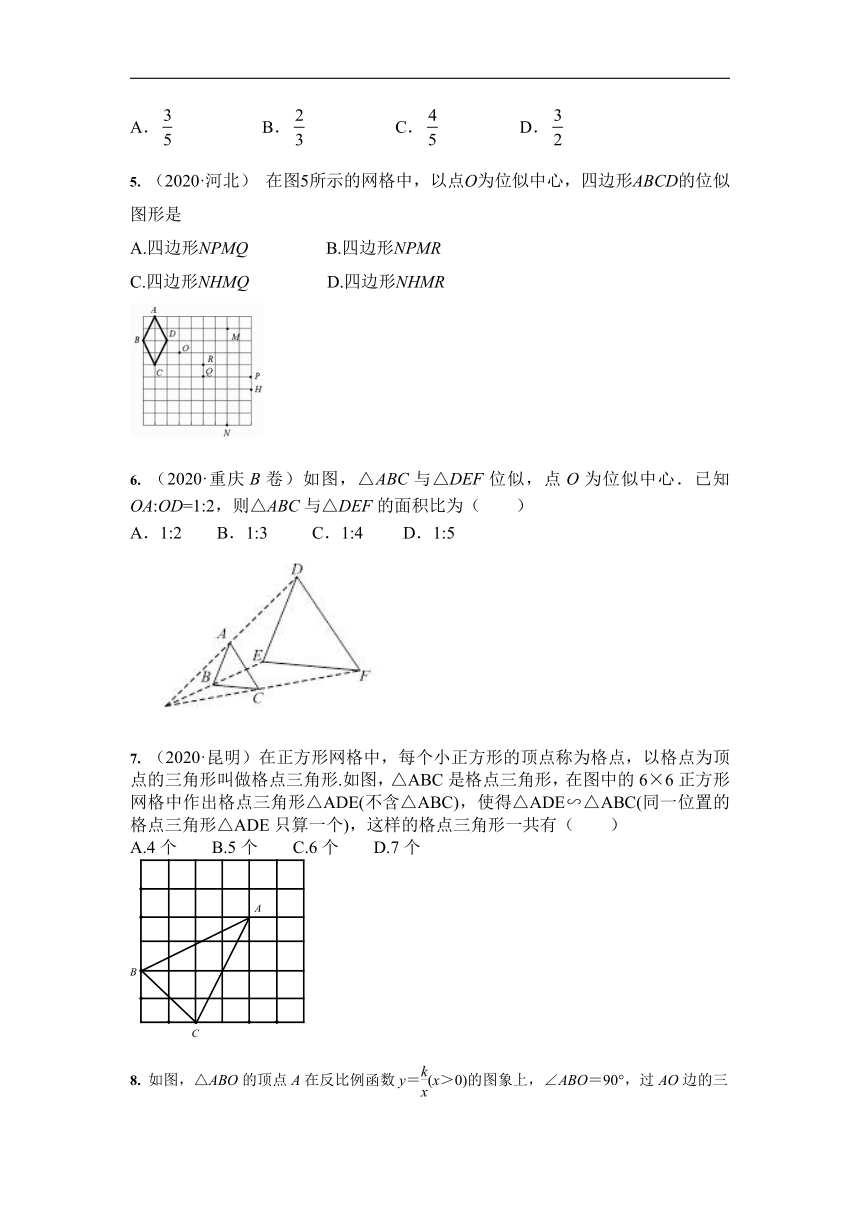
1. 如图,在平面直角坐标系中,以原点O为中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4) B.(-1,-2)
C.(-2,-4) D.(-2,-1)
2. 已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
3. (2020·永州)如图,在中,,四边形的面积为21,则的面积是( )
A. B. 25 C. 35 D. 63
4. (2020·营口)如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
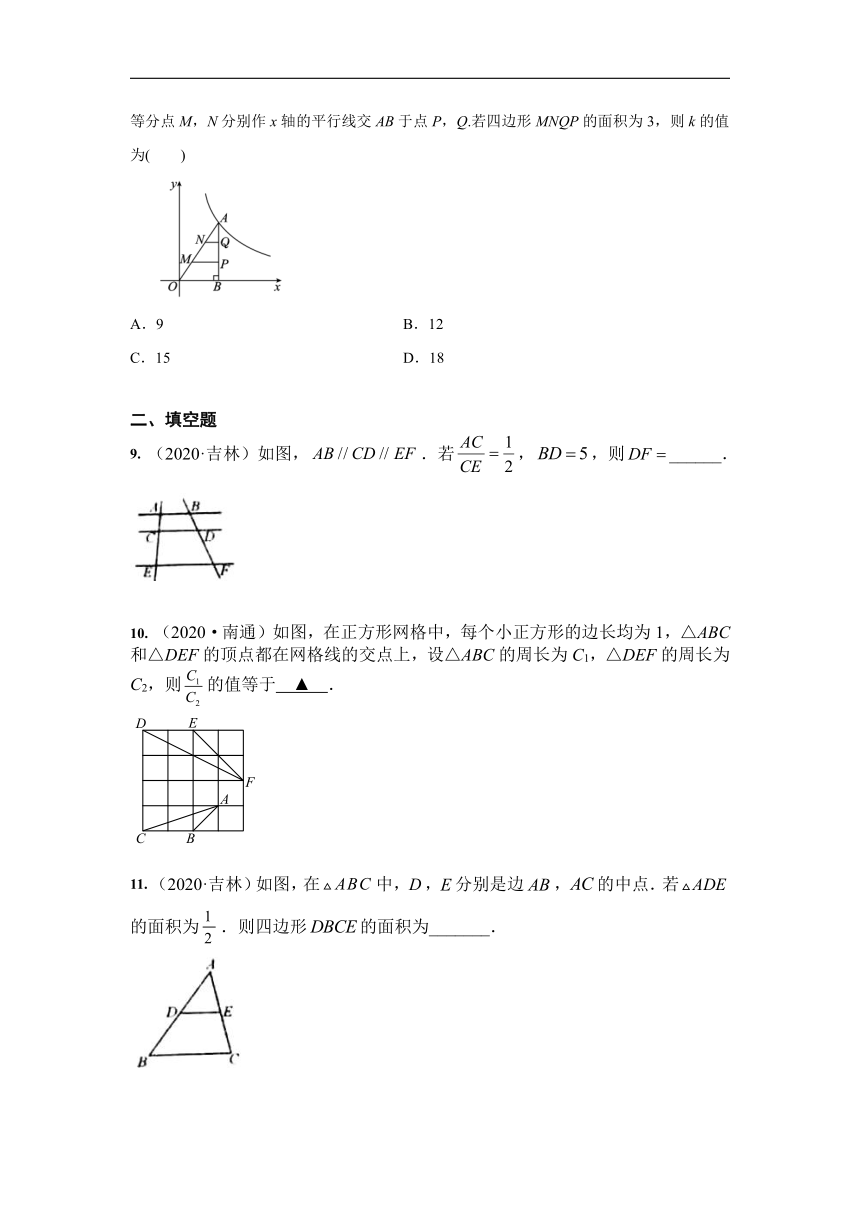
5. (2020·河北) 在图5所示的网格中,以点O为位似中心,四边形ABCD的位似图形是
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
6. (2020·重庆B卷)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
7. (2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
8. 如图,△ABO的顶点A在反比例函数y=(x>0)的图象上,∠ABO=90°,过AO边的三等分点M,N分别作x轴的平行线交AB于点P,Q.若四边形MNQP的面积为3,则k的值为( )
A.9 B.12
C.15 D.18
二、填空题
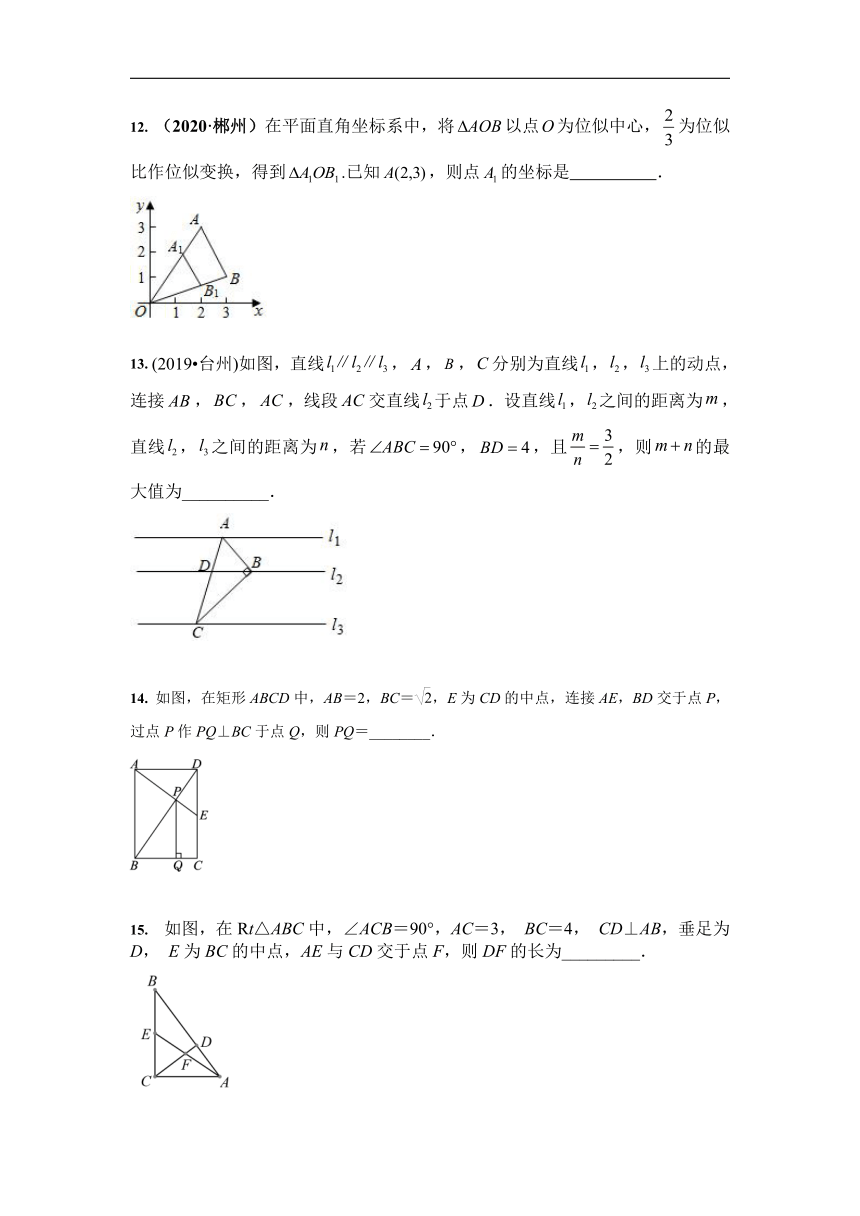
9. (2020·吉林)如图,.若,,则______.
10. (2020·南通)如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则的值等于 ▲ .
11. (2020·吉林)如图,在中,,分别是边,的中点.若的面积为.则四边形的面积为_______.
12. (2020·郴州)在平面直角坐标系中,将以点为位似中心,为位似比作位似变换,得到.已知,则点的坐标是 .
13. (2019?台州)如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为__________.
14. 如图,在矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
15. 如图,在Rt△ABC中,∠ACB=90°,AC=3, BC=4, CD⊥AB,垂足为D, E为BC的中点,AE与CD交于点F,则DF的长为_________.
三、解答题
16. 如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设=.
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
17. (2020·江苏徐州)我们知道:如图①,点B把线段AC分成两部分,如果,那么称点B为线段AC的黄金分割点.它们的比值为.
(1)在图①中,若AC=20cm,则AB的长为 cm;
(2)如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B的对应点H,得折痕CG.试说明:G是AB的黄金分割点;
(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
图① 图 ② 图③
18. (2020?丽水)如图,在△ABC中,AB=4,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
人教版 九年级下册 第27章 相似 课时训练-答案
一、选择题
1. 【答案】C 解析:根据以原点O为位似中心,图形的坐标特点得出,对应点的坐标应乘以-2,故点A的坐标是(1,2),则点A′的坐标是(-2,-4).
2. 【答案】A
3. 【答案】B
【详解】解:∵
∴
∴
∵
∴
∴
∴
∵
∴
∴
故选:B.
4. 【答案】A
【解析】利用平行截割定理求的值.∵DE∥AB,∴==,∵CE+AE=AC,∴=.
5. 【答案】A
【解析】解析:连接AO并延长AO至点N,连接BO并延长PO至点P, 连接CO并延长CO至点M, 连接DO并延长DO至Q,可知,所以以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故答案为A.
6. 【答案】C
【解析】本题考查了相似三角形的性质, ∵△ABC与△DEF位似,且,∴,因此本题选C.
7. 【答案】A
【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:
因此本题选A.
8. 【答案】D [解析] ∵NQ∥MP∥OB,∴△ANQ∽△AMP∽△AOB.∵M,N是OA的三等分点,∴=,=,∴=.
∵四边形MNQP的面积为3,
∴=,∴S△ANQ=1.
∵=()2=,∴S△AOB=9,
∴k=2S△AOB=18.
二、填空题
9. 【答案】10
【解析】∵,∴,
又∵,,∴,∴,故答案为:10.
10. 【答案】
【解析】由图形易证△ABC与△DEF相似,且相似比为,所以周长比为.故答案为:.
11. 【答案】
【解析】点,分别是边,的中点,
,即
又,
则四边形的面积为.
故答案为:.
12. 【答案】(,2)
【解析】∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,A(2,3),∴点A1的坐标是:(×2,×3),即A1(,2).故答案为:(,2).
13. 【答案】
【解析】如图,过作于,延长交于,过作于,过作于,
设,,,,
∵,∴,,
∵,
∴,
∴,∴,
∴,即,∴,
∵,∴,
∴,即,
∴,
∵,∴,
∴,
∴当最大时,,
∵,
∴当时,,
∴,
∴的最大值为.故答案为:.
14. 【答案】 [解析] ∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E为CD的中点,∴DE=CD=AB=1.
∵AB∥CD,∴△ABP∽△EDP,∴=,∴=,∴=.
∵PQ⊥BC,∴PQ∥CD,
∴△BPQ∽△BDC,∴==.
∵CD=2,∴PQ=.
15. 【答案】
【解析】本题考查平行线分线段成比例定理,相似三角形的判定与性质.已知∠ACB=90°,AC=3, BC=4,由勾股定理,得AB=5.CD⊥AB,由三角形的面积,得CD==.易得△ABC∽△ACD∽△CBD,由相似三角形对应边成比例,得AD==,BD==.过点E作EG∥AB交CD于点G,由平行线分线段成比例,得DG=CD=,EG=,所以,即,所以DF=,故答案为.
三、解答题
16. 【答案】
解:(1)证明:∵DE∥AC,
∴∠DEB=∠FCE.
∵EF∥AB,∴∠DBE=∠FEC,
∴△BDE∽△EFC.
(2)①∵EF∥AB,
∴==.
又∵BC=BE+EC=12,
∴BE=4.
②∵=,∴=.
∵EF∥AB,∴△EFC∽△BAC,
∴=2=2=,
∴S△ABC=S△EFC=×20=45.
17. 【答案】
解: (1).解:∵,AC=20,∴AB=.
(2)延长CG交DA的延长线于点J,由折叠可知:∠BCG=∠ECG,
∵AD∥BC,∴∠J=∠BCG=∠ECG,∴JE=CE.由折叠可知:E、F为AD、BC的中点,∴DE=AE=10,
由勾股定理可得:CE=,∴EJ=,∴AJ=JE-AE=-10,
∵AJ∥BC,∴△AGJ∽△BGC,∴,∴G是AB的黄金分割点.
(3)PB=BC,理由如下:∵E为AD的黄金分割点,且AE>DE,∴AE=a.
∵CF⊥BE,∴∠ABE+∠CBE=∠CBE+∠BCF=90?,∴∠ABE=∠FCB,
在△BEA和△CFB中,∵,∴△BEA≌△CFB,∴BF=AE=a.
∴,∵AE∥BP,∴△AEF∽△BPF,∴,
∵AE=BF,∴PB=AB,∴PB=BC.
18. 【答案】
解:(1)如图1中,过点A作AD⊥BC于D.
在Rt△ABD中,AD=AB?sin45°=44.
(2)①如图2中,
∵△AEF≌△PEF,∴AE=EP,∵AE=EB,∴BE=EP,∴∠EPB=∠B=45°,∴∠PEB=90°,∴∠AEP=180°﹣90°=90°.
②如图3中,由(1)可知:AC,
∵PF⊥AC,∴∠PFA=90°,∵△AEF≌△PEF,∴∠AFE=∠PFE=45°,
∴∠AFE=∠B,∵∠EAF=∠CAB,∴△AEF∽△ACB,
∴,即,∴AF=2,在Rt△AFP,AF=FP,
∴APAF=2.
一、选择题
1. 如图,在平面直角坐标系中,以原点O为中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4) B.(-1,-2)
C.(-2,-4) D.(-2,-1)
2. 已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
3. (2020·永州)如图,在中,,四边形的面积为21,则的面积是( )
A. B. 25 C. 35 D. 63
4. (2020·营口)如图,在△ABC中,DE∥AB,且=,则的值为( )
A. B. C. D.
5. (2020·河北) 在图5所示的网格中,以点O为位似中心,四边形ABCD的位似图形是
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
6. (2020·重庆B卷)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
7. (2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
8. 如图,△ABO的顶点A在反比例函数y=(x>0)的图象上,∠ABO=90°,过AO边的三等分点M,N分别作x轴的平行线交AB于点P,Q.若四边形MNQP的面积为3,则k的值为( )
A.9 B.12
C.15 D.18
二、填空题
9. (2020·吉林)如图,.若,,则______.
10. (2020·南通)如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则的值等于 ▲ .
11. (2020·吉林)如图,在中,,分别是边,的中点.若的面积为.则四边形的面积为_______.
12. (2020·郴州)在平面直角坐标系中,将以点为位似中心,为位似比作位似变换,得到.已知,则点的坐标是 .
13. (2019?台州)如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为__________.
14. 如图,在矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
15. 如图,在Rt△ABC中,∠ACB=90°,AC=3, BC=4, CD⊥AB,垂足为D, E为BC的中点,AE与CD交于点F,则DF的长为_________.
三、解答题
16. 如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设=.
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
17. (2020·江苏徐州)我们知道:如图①,点B把线段AC分成两部分,如果,那么称点B为线段AC的黄金分割点.它们的比值为.
(1)在图①中,若AC=20cm,则AB的长为 cm;
(2)如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B的对应点H,得折痕CG.试说明:G是AB的黄金分割点;
(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.
图① 图 ② 图③
18. (2020?丽水)如图,在△ABC中,AB=4,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
人教版 九年级下册 第27章 相似 课时训练-答案
一、选择题
1. 【答案】C 解析:根据以原点O为位似中心,图形的坐标特点得出,对应点的坐标应乘以-2,故点A的坐标是(1,2),则点A′的坐标是(-2,-4).
2. 【答案】A
3. 【答案】B
【详解】解:∵
∴
∴
∵
∴
∴
∴
∵
∴
∴
故选:B.
4. 【答案】A
【解析】利用平行截割定理求的值.∵DE∥AB,∴==,∵CE+AE=AC,∴=.
5. 【答案】A
【解析】解析:连接AO并延长AO至点N,连接BO并延长PO至点P, 连接CO并延长CO至点M, 连接DO并延长DO至Q,可知,所以以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故答案为A.
6. 【答案】C
【解析】本题考查了相似三角形的性质, ∵△ABC与△DEF位似,且,∴,因此本题选C.
7. 【答案】A
【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:
因此本题选A.
8. 【答案】D [解析] ∵NQ∥MP∥OB,∴△ANQ∽△AMP∽△AOB.∵M,N是OA的三等分点,∴=,=,∴=.
∵四边形MNQP的面积为3,
∴=,∴S△ANQ=1.
∵=()2=,∴S△AOB=9,
∴k=2S△AOB=18.
二、填空题
9. 【答案】10
【解析】∵,∴,
又∵,,∴,∴,故答案为:10.
10. 【答案】
【解析】由图形易证△ABC与△DEF相似,且相似比为,所以周长比为.故答案为:.
11. 【答案】
【解析】点,分别是边,的中点,
,即
又,
则四边形的面积为.
故答案为:.
12. 【答案】(,2)
【解析】∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,A(2,3),∴点A1的坐标是:(×2,×3),即A1(,2).故答案为:(,2).
13. 【答案】
【解析】如图,过作于,延长交于,过作于,过作于,
设,,,,
∵,∴,,
∵,
∴,
∴,∴,
∴,即,∴,
∵,∴,
∴,即,
∴,
∵,∴,
∴,
∴当最大时,,
∵,
∴当时,,
∴,
∴的最大值为.故答案为:.
14. 【答案】 [解析] ∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E为CD的中点,∴DE=CD=AB=1.
∵AB∥CD,∴△ABP∽△EDP,∴=,∴=,∴=.
∵PQ⊥BC,∴PQ∥CD,
∴△BPQ∽△BDC,∴==.
∵CD=2,∴PQ=.
15. 【答案】
【解析】本题考查平行线分线段成比例定理,相似三角形的判定与性质.已知∠ACB=90°,AC=3, BC=4,由勾股定理,得AB=5.CD⊥AB,由三角形的面积,得CD==.易得△ABC∽△ACD∽△CBD,由相似三角形对应边成比例,得AD==,BD==.过点E作EG∥AB交CD于点G,由平行线分线段成比例,得DG=CD=,EG=,所以,即,所以DF=,故答案为.
三、解答题
16. 【答案】
解:(1)证明:∵DE∥AC,
∴∠DEB=∠FCE.
∵EF∥AB,∴∠DBE=∠FEC,
∴△BDE∽△EFC.
(2)①∵EF∥AB,
∴==.
又∵BC=BE+EC=12,
∴BE=4.
②∵=,∴=.
∵EF∥AB,∴△EFC∽△BAC,
∴=2=2=,
∴S△ABC=S△EFC=×20=45.
17. 【答案】
解: (1).解:∵,AC=20,∴AB=.
(2)延长CG交DA的延长线于点J,由折叠可知:∠BCG=∠ECG,
∵AD∥BC,∴∠J=∠BCG=∠ECG,∴JE=CE.由折叠可知:E、F为AD、BC的中点,∴DE=AE=10,
由勾股定理可得:CE=,∴EJ=,∴AJ=JE-AE=-10,
∵AJ∥BC,∴△AGJ∽△BGC,∴,∴G是AB的黄金分割点.
(3)PB=BC,理由如下:∵E为AD的黄金分割点,且AE>DE,∴AE=a.
∵CF⊥BE,∴∠ABE+∠CBE=∠CBE+∠BCF=90?,∴∠ABE=∠FCB,
在△BEA和△CFB中,∵,∴△BEA≌△CFB,∴BF=AE=a.
∴,∵AE∥BP,∴△AEF∽△BPF,∴,
∵AE=BF,∴PB=AB,∴PB=BC.
18. 【答案】
解:(1)如图1中,过点A作AD⊥BC于D.
在Rt△ABD中,AD=AB?sin45°=44.
(2)①如图2中,
∵△AEF≌△PEF,∴AE=EP,∵AE=EB,∴BE=EP,∴∠EPB=∠B=45°,∴∠PEB=90°,∴∠AEP=180°﹣90°=90°.
②如图3中,由(1)可知:AC,
∵PF⊥AC,∴∠PFA=90°,∵△AEF≌△PEF,∴∠AFE=∠PFE=45°,
∴∠AFE=∠B,∵∠EAF=∠CAB,∴△AEF∽△ACB,
∴,即,∴AF=2,在Rt△AFP,AF=FP,
∴APAF=2.
