1.6 利用三角函数测高 课件(共23张PPT)
文档属性
| 名称 | 1.6 利用三角函数测高 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 10:44:06 | ||
图片预览






文档简介
第6节 利用三角函数测高
第一章 直角三角形的边角关系
2020-2021北师大版九年级数学下册
1.能够设计活动方案、自制测倾器和运用测倾器进行实地测量以及撰写活动报告的过程;
2.能够对所得的数据进行整理、分析和矫正。
学习目标
看一看:观察下图中的建筑及其高度,想一想人们是如何准确测出它们的实际高度的。
哈利法塔原名迪拜塔,又称迪拜大厦或比斯迪拜塔,塔高828米,楼层总数162层。
上海中心大厦建筑主体为119层,总高为632米,结构高度为580米,
新课导入
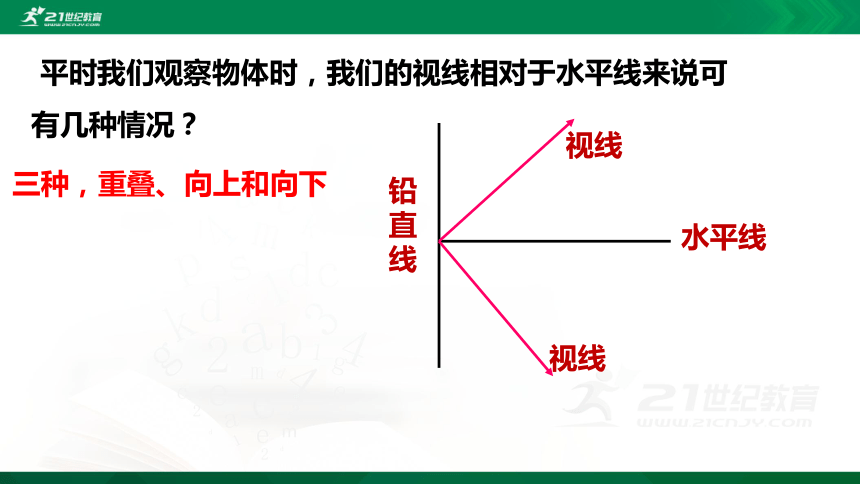
平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
三种,重叠、向上和向下
铅直线
水平线
视线
视线
测量中的视角问题
知识点一
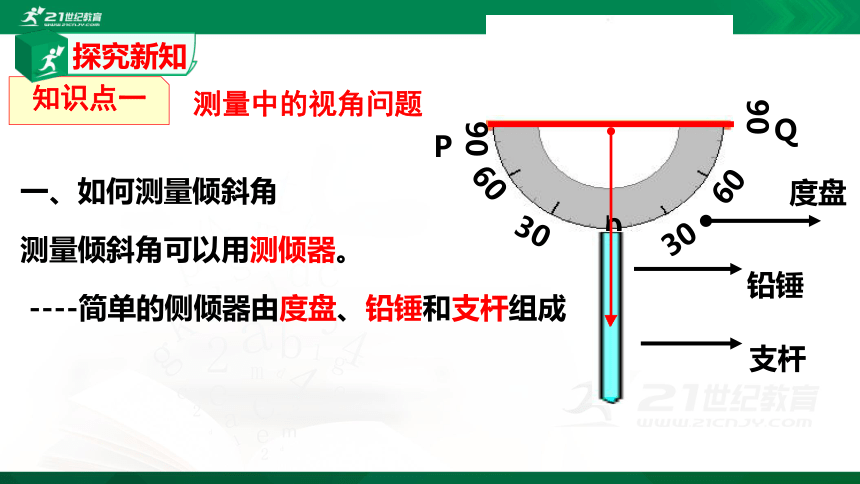
一、如何测量倾斜角
测量倾斜角可以用测倾器。
----简单的侧倾器由度盘、铅锤和支杆组成
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
探究新知
0
30
30
60
60
90
90
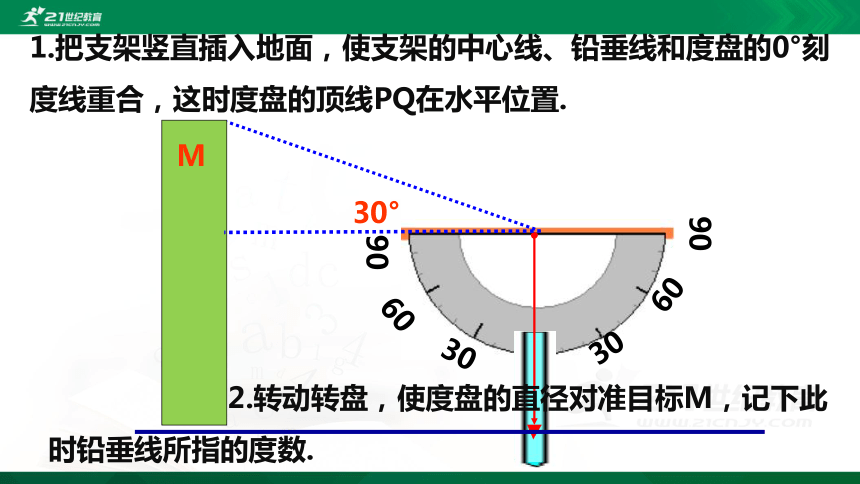
2.转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
M
30°
1.把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
例1 如图小山岗的斜坡AC的坡度是坡角为α,在与山脚C距离200 m的点D处测得山顶A的仰角为26.6°,求小山岗的高.(结果精确到1 m,参考数据:sin26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50)
例题讲解
设小山岗的高为x m,
在Rt△ABC中,由题意得 tan α=
∴BC=
∴BD=DC+BC=
在Rt△ABD中,tan ∠ADB=tan 26.6°=
∴ 解得x≈300,即小山岗的高约为300 m.
解:
总结:与仰角(或俯角)有关的计算问题的解决方法:
首先弄清哪个角是仰角(或俯角),再选择或构造恰当的直角三角形,将仰角或俯角置于这个三角形中,选择正确的三角函数,并借助计算器求出要求的量.
例2 如图,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在N处看塔顶,仰角为60°.
乙:我站在M处看塔顶,仰角为30°.
甲:我们的身高都是1.5 m.
乙:我们和塔在一条直线上,且我们相距20 m.请你根据两位同学的对话,计算白塔的高度.(结果精确到1 m).
例题讲解
由题意知∠CAB=30°,∠CBD=60°,AB=20 m,AM=BN=DP=1.5 m.
在△ABC中,∠CBD=∠ACB+∠CAB,
∴∠ACB=60°-30°=30°.
∴∠ACB=∠CAB.∴BC=AB=20 m.
在Rt△CBD中,BC=20 m,∠CBD=60°,sin ∠CBD=
∴CD=BC·sin ∠CBD=20sin 60°=20× (m).
∴CP=CD+DP=10 +1.5≈19(m).
答:白塔的高度约为19 m.
解:
例3 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°,如图所示.已知大桥BC与地面在同一水平面上,其长度为100 m.请求出热气球离地面
的高度.(结果保留整数.
参考数据:sin 35°≈0.574,
cos 35°≈0.819,tan 35°≈0.700)
例题讲解
如图,作AD⊥BC于点D.由题意得∠ABD=45°,
∠ACD=35°,BC=100 m.
设AD=x m,则BD=AD=x m,CD= m.
∵BC=CD-BD,∴ -x=100.
∴x≈233.
答:热气球离地面的高度约为233 m.
解:
总结:从同一点看不同的位置,有两个视角,不同位置之间有距离,作垂线将两个视角都放在直角三角形中,利用不同位置之间的距离列方程来解决问题.
1.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米
课堂练习
2.如图,山顶有一座电视塔,在地面上一点A处测得塔顶B处的仰角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60米,则山高CD等于( )
A.30(1+ )米
B.30( -1)米
C.30 米
D.(30 +1)米
3.如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120 m,则这栋楼的高度为( )
A.160 m
B.120 m
C.300 m
D.160 m
4.湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米
5.如图,某建筑物BC上有一旗杆AB,从与BC相距38 m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为________
(结果精确到0.1 m.参考数据:sin 50°≈0.77,
cos50°≈0.64,tan 50°≈1.19).
6.目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B
的仰角为45°,在楼顶D处测得塔顶B的仰角为
39°.(tan39°≈0.81)
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米)
A
B
C
D
E
39°
45°
利用三角函数测高
测量底部可以到达的物体的高度
测量底部不可以到达的物体的高度
课堂小结
谢谢聆听
第一章 直角三角形的边角关系
2020-2021北师大版九年级数学下册
1.能够设计活动方案、自制测倾器和运用测倾器进行实地测量以及撰写活动报告的过程;
2.能够对所得的数据进行整理、分析和矫正。
学习目标
看一看:观察下图中的建筑及其高度,想一想人们是如何准确测出它们的实际高度的。
哈利法塔原名迪拜塔,又称迪拜大厦或比斯迪拜塔,塔高828米,楼层总数162层。
上海中心大厦建筑主体为119层,总高为632米,结构高度为580米,
新课导入
平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?
三种,重叠、向上和向下
铅直线
水平线
视线
视线
测量中的视角问题
知识点一
一、如何测量倾斜角
测量倾斜角可以用测倾器。
----简单的侧倾器由度盘、铅锤和支杆组成
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
探究新知
0
30
30
60
60
90
90
2.转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
M
30°
1.把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
例1 如图小山岗的斜坡AC的坡度是坡角为α,在与山脚C距离200 m的点D处测得山顶A的仰角为26.6°,求小山岗的高.(结果精确到1 m,参考数据:sin26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50)
例题讲解
设小山岗的高为x m,
在Rt△ABC中,由题意得 tan α=
∴BC=
∴BD=DC+BC=
在Rt△ABD中,tan ∠ADB=tan 26.6°=
∴ 解得x≈300,即小山岗的高约为300 m.
解:
总结:与仰角(或俯角)有关的计算问题的解决方法:
首先弄清哪个角是仰角(或俯角),再选择或构造恰当的直角三角形,将仰角或俯角置于这个三角形中,选择正确的三角函数,并借助计算器求出要求的量.
例2 如图,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在N处看塔顶,仰角为60°.
乙:我站在M处看塔顶,仰角为30°.
甲:我们的身高都是1.5 m.
乙:我们和塔在一条直线上,且我们相距20 m.请你根据两位同学的对话,计算白塔的高度.(结果精确到1 m).
例题讲解
由题意知∠CAB=30°,∠CBD=60°,AB=20 m,AM=BN=DP=1.5 m.
在△ABC中,∠CBD=∠ACB+∠CAB,
∴∠ACB=60°-30°=30°.
∴∠ACB=∠CAB.∴BC=AB=20 m.
在Rt△CBD中,BC=20 m,∠CBD=60°,sin ∠CBD=
∴CD=BC·sin ∠CBD=20sin 60°=20× (m).
∴CP=CD+DP=10 +1.5≈19(m).
答:白塔的高度约为19 m.
解:
例3 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°,如图所示.已知大桥BC与地面在同一水平面上,其长度为100 m.请求出热气球离地面
的高度.(结果保留整数.
参考数据:sin 35°≈0.574,
cos 35°≈0.819,tan 35°≈0.700)
例题讲解
如图,作AD⊥BC于点D.由题意得∠ABD=45°,
∠ACD=35°,BC=100 m.
设AD=x m,则BD=AD=x m,CD= m.
∵BC=CD-BD,∴ -x=100.
∴x≈233.
答:热气球离地面的高度约为233 m.
解:
总结:从同一点看不同的位置,有两个视角,不同位置之间有距离,作垂线将两个视角都放在直角三角形中,利用不同位置之间的距离列方程来解决问题.
1.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米
课堂练习
2.如图,山顶有一座电视塔,在地面上一点A处测得塔顶B处的仰角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60米,则山高CD等于( )
A.30(1+ )米
B.30( -1)米
C.30 米
D.(30 +1)米
3.如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120 m,则这栋楼的高度为( )
A.160 m
B.120 m
C.300 m
D.160 m
4.湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )(参考数据:sin 41.5°≈0.663,cos 41.5°≈0.749,tan 41.5°≈0.885)
A.34米 B.38米
C.45米 D.50米
5.如图,某建筑物BC上有一旗杆AB,从与BC相距38 m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为________
(结果精确到0.1 m.参考数据:sin 50°≈0.77,
cos50°≈0.64,tan 50°≈1.19).
6.目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B
的仰角为45°,在楼顶D处测得塔顶B的仰角为
39°.(tan39°≈0.81)
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米)
A
B
C
D
E
39°
45°
利用三角函数测高
测量底部可以到达的物体的高度
测量底部不可以到达的物体的高度
课堂小结
谢谢聆听
