1.5 三角函数的应用 课件(共20张PPT)
文档属性
| 名称 | 1.5 三角函数的应用 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 13:51:22 | ||
图片预览






文档简介
第5节 三角函数的应用
第一章 直角三角形的边角关系
2020-2021北师大版九年级数学下册
1.正确理解方位角、仰角和坡角的概念;(重点)
2.能运用解直角三角形知识解决方位角、仰角和坡角的问题.(难点)
学习目标
我们已经知道轮船在海中航行时,可以用方位角准确描述它的航行方向.
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
新课导入
利用解直角三角形的知识解一般实际应用问题
知识点一
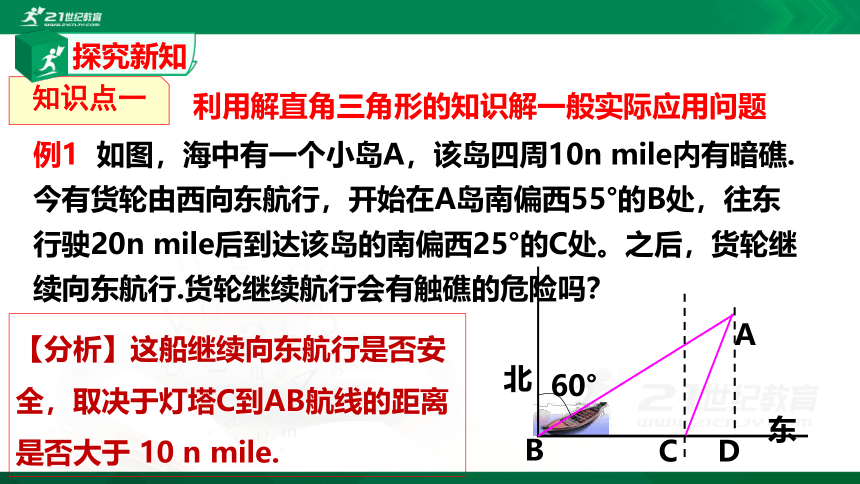
例1 如图,海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处。之后,货轮继续向东航行.货轮继续航行会有触礁的危险吗?
B
A
C
60°
D
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于 10 n mile.
北
东
探究新知
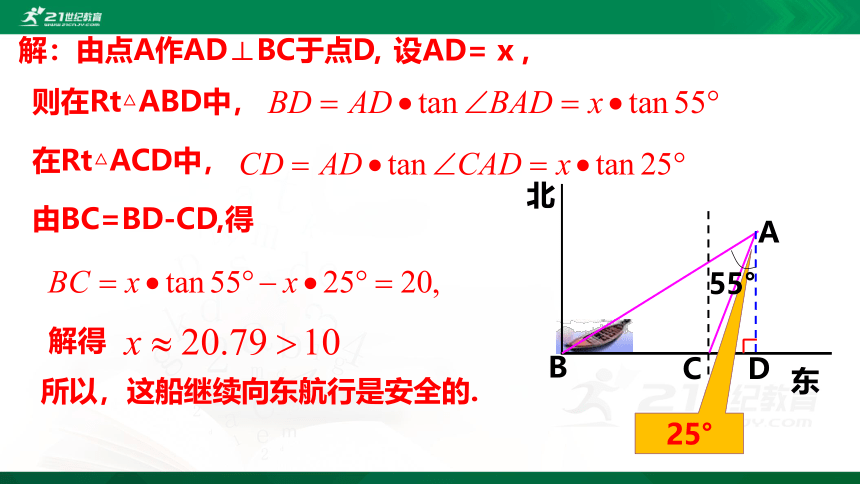
解:由点A作AD⊥BC于点D,
设AD= x ,
则在Rt△ABD中,
在Rt△ACD中,
解得
所以,这船继续向东航行是安全的.
B
A
C
D
25°
55°
北
东
由BC=BD-CD,得
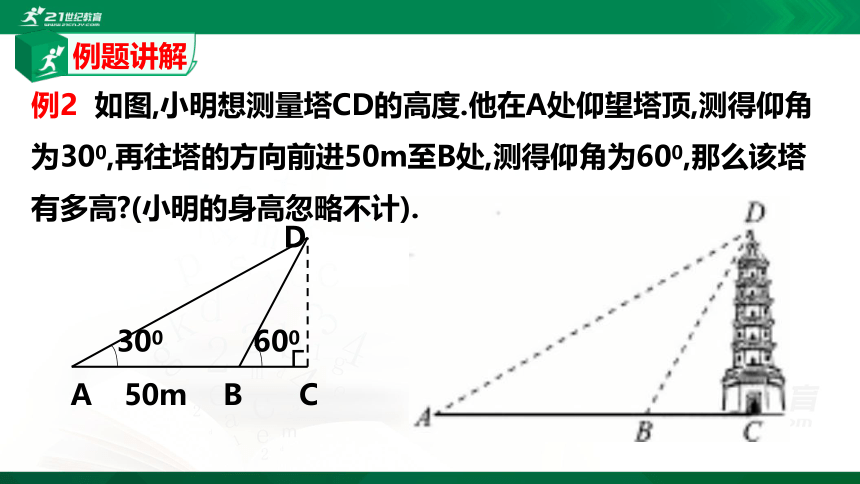
例2 如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计).
D
A
B
C
┌
50m
300
600
例题讲解
设CD长为x米,则∠ADC=60?,∠BDC=30?,
解:如图,根据题意知,∠A=300,∠DBC=600,AB=50m.求CD的长
在Rt△ADC中,tan60?=
在Rt△BDC中,tan30?=
∵AC-BC=AB
(
)
.
3
25
3
3
3
50
30
tan
60
tan
50
0
0
m
x
=
-
=
-
=
D
A
B
C
┌
50m
300
600
答:该塔约有 m高.
3
25
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
方法归纳
例3 如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)
分析:求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解,所以要用方程思想,先把AC看成已知,用含AC的代数式表示BC和DC,由BD=1000m建立关于AC的方程,从而求得AC.
例题讲解
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
例4 如图,一幢楼房AB背后有一台阶CD,台阶每层高0.2 m,且 AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°
时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在台阶的MN这层上晒太阳( 取1.73).
(1)求楼房的高度约为多少米.
(2)过了一会儿,当α=45°时,
请说明理由.
例题讲解
(1)当α=60°时,在Rt△ABE中,
∵tan 60°=
∴AB=10·tan 60°=10 ≈10×1.73=17.3(m).
即楼房的高度约为17.3 m.
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:假设没有台阶,当α=45°时,从点B射
下的光线与地面AD的交点为点F,与射线CM的交点
为点H(如下图).
解:
∵∠BFA=45°,
∴tan 45°= =1,此时的影长AF=AB≈17.3m.
∴CF=AF-AC≈17.3-17.2=0.1(m).∴CH=CF≈0.1 m.
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳。
1.如图,AB是斜靠在墙上的长梯,D是梯上一点,梯脚B与墙脚的距离为1.6 m(即BC的长),点D与墙的距离为1.4 m(即DE的长),BD长为0.55 m,则梯子的长为( )
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
课堂练习
2.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
3.如图,已知电线杆AB直立于地面上,它的影子恰好照在土坡的坡面CD和地面BC上,如果CD与地面成45°,∠A=60°,CD=4 m,BC=(4 -2 ) m,则电线杆AB的长为_______.
4.水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度为1∶3,斜坡CD的坡度为1∶2.5,求:
(1)坝底AD与斜坡AB的长度(精确到0.1m );
(2)斜坡CD的坡角α(精确到 1°).
E
F
A
D
B
C
1:2.5
23
6
α
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
课堂小结
谢谢聆听
第一章 直角三角形的边角关系
2020-2021北师大版九年级数学下册
1.正确理解方位角、仰角和坡角的概念;(重点)
2.能运用解直角三角形知识解决方位角、仰角和坡角的问题.(难点)
学习目标
我们已经知道轮船在海中航行时,可以用方位角准确描述它的航行方向.
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
新课导入
利用解直角三角形的知识解一般实际应用问题
知识点一
例1 如图,海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处。之后,货轮继续向东航行.货轮继续航行会有触礁的危险吗?
B
A
C
60°
D
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于 10 n mile.
北
东
探究新知
解:由点A作AD⊥BC于点D,
设AD= x ,
则在Rt△ABD中,
在Rt△ACD中,
解得
所以,这船继续向东航行是安全的.
B
A
C
D
25°
55°
北
东
由BC=BD-CD,得
例2 如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计).
D
A
B
C
┌
50m
300
600
例题讲解
设CD长为x米,则∠ADC=60?,∠BDC=30?,
解:如图,根据题意知,∠A=300,∠DBC=600,AB=50m.求CD的长
在Rt△ADC中,tan60?=
在Rt△BDC中,tan30?=
∵AC-BC=AB
(
)
.
3
25
3
3
3
50
30
tan
60
tan
50
0
0
m
x
=
-
=
-
=
D
A
B
C
┌
50m
300
600
答:该塔约有 m高.
3
25
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
方法归纳
例3 如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)
分析:求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解,所以要用方程思想,先把AC看成已知,用含AC的代数式表示BC和DC,由BD=1000m建立关于AC的方程,从而求得AC.
例题讲解
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
例4 如图,一幢楼房AB背后有一台阶CD,台阶每层高0.2 m,且 AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°
时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在台阶的MN这层上晒太阳( 取1.73).
(1)求楼房的高度约为多少米.
(2)过了一会儿,当α=45°时,
请说明理由.
例题讲解
(1)当α=60°时,在Rt△ABE中,
∵tan 60°=
∴AB=10·tan 60°=10 ≈10×1.73=17.3(m).
即楼房的高度约为17.3 m.
(2)当α=45°时,小猫仍可以晒到太阳.
理由如下:假设没有台阶,当α=45°时,从点B射
下的光线与地面AD的交点为点F,与射线CM的交点
为点H(如下图).
解:
∵∠BFA=45°,
∴tan 45°= =1,此时的影长AF=AB≈17.3m.
∴CF=AF-AC≈17.3-17.2=0.1(m).∴CH=CF≈0.1 m.
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳。
1.如图,AB是斜靠在墙上的长梯,D是梯上一点,梯脚B与墙脚的距离为1.6 m(即BC的长),点D与墙的距离为1.4 m(即DE的长),BD长为0.55 m,则梯子的长为( )
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
课堂练习
2.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
3.如图,已知电线杆AB直立于地面上,它的影子恰好照在土坡的坡面CD和地面BC上,如果CD与地面成45°,∠A=60°,CD=4 m,BC=(4 -2 ) m,则电线杆AB的长为_______.
4.水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度为1∶3,斜坡CD的坡度为1∶2.5,求:
(1)坝底AD与斜坡AB的长度(精确到0.1m );
(2)斜坡CD的坡角α(精确到 1°).
E
F
A
D
B
C
1:2.5
23
6
α
利用解直角三角形的知识解决实际问题的一般过程:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解
直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数,运用直
角三角形的有关性质解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
课堂小结
谢谢聆听
