1.1.1 锐角三角函数(第1课时) 课件(共25张PPT)
文档属性
| 名称 | 1.1.1 锐角三角函数(第1课时) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 13:56:50 | ||
图片预览






文档简介
第1节 锐角三角函数
(第1课时)
第一章 直角三角形的边角关系
2020-2021北师大版九年级数学下册
1.经历探索直角三角形中某锐角确定后其对边与邻边的比值也随之确定的过程,理解正切的意义.
2.能够用表示直角三角形中两边的比,表示生活中物体的倾斜程度,并能够用正切进行简单的计算.
学习目标
生活中的梯子
新课导入
思考:衡量山“险”与“不险”的标准是什么呢?
陡
陡意味着倾斜程度大!
正切
知识点一
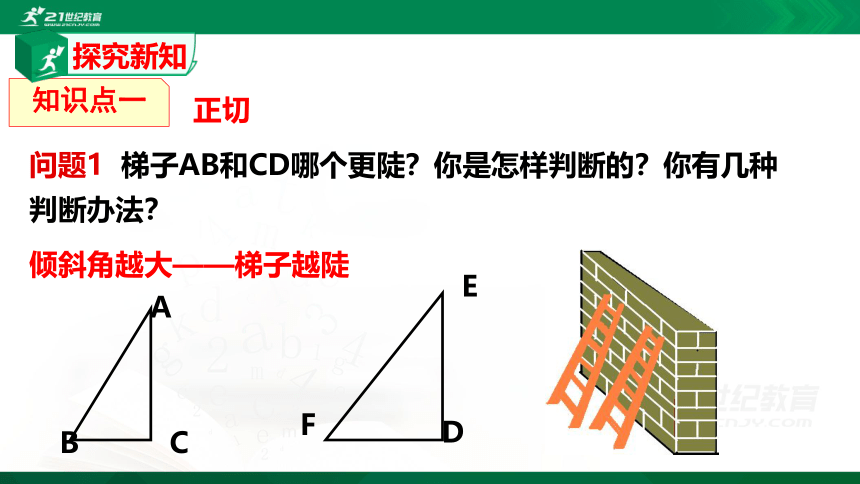
问题1 梯子AB和CD哪个更陡?你是怎样判断的?你有几种判断办法?
A
B
C
D
E
F
倾斜角越大——梯子越陡
探究新知
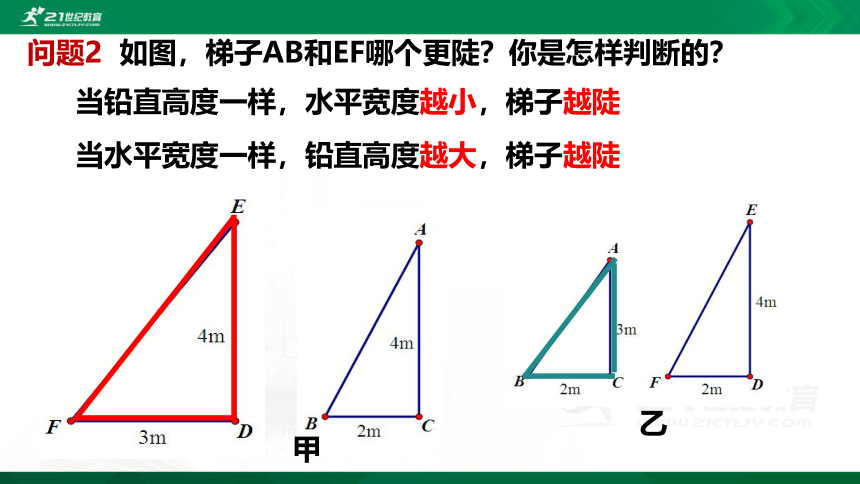
问题2 如图,梯子AB和EF哪个更陡?你是怎样判断的?
当铅直高度一样,水平宽度越小,梯子越陡
当水平宽度一样,铅直高度越大,梯子越陡
甲
乙
问题3 如图,梯子AB和EF哪个更陡?你是怎样判断的?
当铅直高度与水平宽度的比相等时,梯子一样陡
3m
6m
D
E
F
C
2m
B
4m
A
如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;
而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.
你同意小亮的看法吗?
想一想
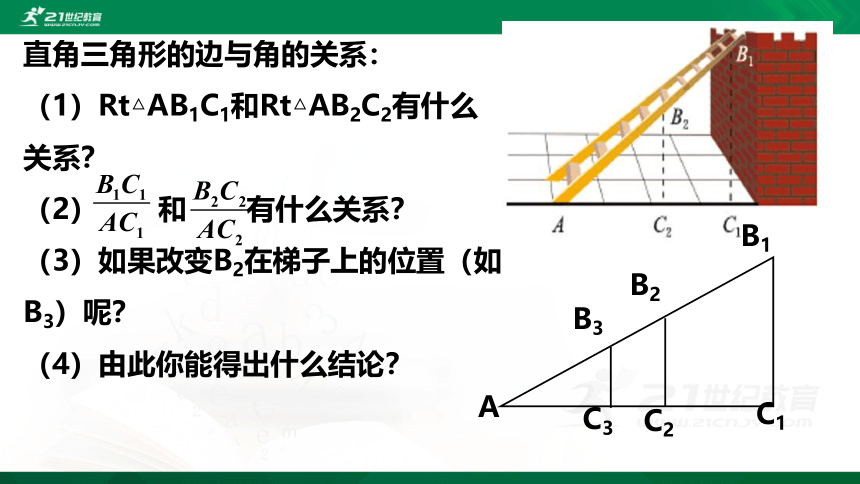
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
(3)如果改变B2在梯子上的位置(如B3)呢?
(4)由此你能得出什么结论?
A
B1
B2
B3
C1
C2
C3
A
B1
B2
B3
C1
C2
C3
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
Rt△AB1C1∽Rt△AB2C2
(3)如果改变B2在梯子上的位置(如B3)呢?
∵Rt△AB1C1∽Rt△AB2C2,即
(4)由此你能得出什么结论?
比值不变
直角三角形中,锐角大小确定后,对应的对边和邻边的比值也就确定了
例1 如图,在Rt△ABC中,∠C=90°,
则tan A=________.
例题讲解
总结:直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利用勾股定理求出未知的直角边,再利用正切的定义求解.
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
正切的定义
在Rt△ABC中,
如果
锐角A确定,
那么
∠A的对边与邻边的比
随之确定,
这个比叫做
∠A的正切.
记作:tanA
读?
结论:tanA的值越大,梯子越陡.
议一议
总结:1.当梯子与地面所成的角为锐角A时,
tan A= tan A的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2. 当倾斜角确定时,其对边与邻边之比随之确定,这一比
值只与倾斜角的大小有关,而与物体的长度无关.
例3 如图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
解:甲梯中, 乙梯中,
因为tanα>tanβ,所以甲梯更陡.
例题讲解
总结:(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾
斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程度,因为夹角的正切值越大,则夹角越大,物体放置得越“陡”.
正切与坡度(角)的关系
知识点二
探究
如图是某一大坝的横断面:
坡面AB的垂直高度与水平宽度AE的长度之比是α的什么三角函数?
α
A
C
B
D
E
坡面AB与水平面的夹角叫做坡角.
坡度的定义:
坡面的垂直高度与水平宽度之比叫做坡度,记作 i .
α
A
B
E
h
l
坡度的概念,一要记住是一个比值而不是角度, 二要明确坡度其实就是坡角的正切.
例4 如图所示,梯形护坡石坝的斜坡AB的坡度为1∶3,坝高BC=2米,则斜坡AB的长是( )
解析:∵∠ACB=90°,坡度为1∶3,
∵BC=2米,∴AC=3BC=3×2=6(米).
例题讲解
1.一个直角三角形中,如果各边的长度都扩大为原来
的2倍,那么它的两个锐角的正切值( )
A.都没有变化 B.都扩大为原来的2倍
C.都缩小为原来的一半 D.不能确定是否发生变化
课堂练习
2.以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
3.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tan A的值是( )
A. B. C. D.
4.在Rt△ABC中,CD为斜边AB上的高,且CD=2,BD=8,则tan A的值是( )
A.2 B.4 C. D.
5.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tan B的值是( )
A. B. 3 C. D.
6.如图, △ABC是等腰三角形,你能根据图中所给数据求出tanC吗?
B
C
正切:∠A的对边与邻边的比叫做∠A的正切,记作tan A, 即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
正切与坡度(角)的关系:坡度就是坡角的正切.
课堂小结
谢谢聆听
(第1课时)
第一章 直角三角形的边角关系
2020-2021北师大版九年级数学下册
1.经历探索直角三角形中某锐角确定后其对边与邻边的比值也随之确定的过程,理解正切的意义.
2.能够用表示直角三角形中两边的比,表示生活中物体的倾斜程度,并能够用正切进行简单的计算.
学习目标
生活中的梯子
新课导入
思考:衡量山“险”与“不险”的标准是什么呢?
陡
陡意味着倾斜程度大!
正切
知识点一
问题1 梯子AB和CD哪个更陡?你是怎样判断的?你有几种判断办法?
A
B
C
D
E
F
倾斜角越大——梯子越陡
探究新知
问题2 如图,梯子AB和EF哪个更陡?你是怎样判断的?
当铅直高度一样,水平宽度越小,梯子越陡
当水平宽度一样,铅直高度越大,梯子越陡
甲
乙
问题3 如图,梯子AB和EF哪个更陡?你是怎样判断的?
当铅直高度与水平宽度的比相等时,梯子一样陡
3m
6m
D
E
F
C
2m
B
4m
A
如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;
而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.
你同意小亮的看法吗?
想一想
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
(3)如果改变B2在梯子上的位置(如B3)呢?
(4)由此你能得出什么结论?
A
B1
B2
B3
C1
C2
C3
A
B1
B2
B3
C1
C2
C3
直角三角形的边与角的关系:
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
(2) 和 有什么关系?
Rt△AB1C1∽Rt△AB2C2
(3)如果改变B2在梯子上的位置(如B3)呢?
∵Rt△AB1C1∽Rt△AB2C2,即
(4)由此你能得出什么结论?
比值不变
直角三角形中,锐角大小确定后,对应的对边和邻边的比值也就确定了
例1 如图,在Rt△ABC中,∠C=90°,
则tan A=________.
例题讲解
总结:直角三角形中求锐角正切值的方法:
(1)若已知两直角边,直接利用正切的定义求解;
(2)若已知一直角边及斜边,另一直角边未知,可先利用勾股定理求出未知的直角边,再利用正切的定义求解.
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
正切的定义
在Rt△ABC中,
如果
锐角A确定,
那么
∠A的对边与邻边的比
随之确定,
这个比叫做
∠A的正切.
记作:tanA
读?
结论:tanA的值越大,梯子越陡.
议一议
总结:1.当梯子与地面所成的角为锐角A时,
tan A= tan A的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2. 当倾斜角确定时,其对边与邻边之比随之确定,这一比
值只与倾斜角的大小有关,而与物体的长度无关.
例3 如图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
解:甲梯中, 乙梯中,
因为tanα>tanβ,所以甲梯更陡.
例题讲解
总结:(1)倾斜程度,其本意指倾斜角的大小,一般来说,倾
斜角较大的物体,就说它放得更“陡”.
(2)利用物体与地面夹角的正切值来判断物体的倾斜程度,因为夹角的正切值越大,则夹角越大,物体放置得越“陡”.
正切与坡度(角)的关系
知识点二
探究
如图是某一大坝的横断面:
坡面AB的垂直高度与水平宽度AE的长度之比是α的什么三角函数?
α
A
C
B
D
E
坡面AB与水平面的夹角叫做坡角.
坡度的定义:
坡面的垂直高度与水平宽度之比叫做坡度,记作 i .
α
A
B
E
h
l
坡度的概念,一要记住是一个比值而不是角度, 二要明确坡度其实就是坡角的正切.
例4 如图所示,梯形护坡石坝的斜坡AB的坡度为1∶3,坝高BC=2米,则斜坡AB的长是( )
解析:∵∠ACB=90°,坡度为1∶3,
∵BC=2米,∴AC=3BC=3×2=6(米).
例题讲解
1.一个直角三角形中,如果各边的长度都扩大为原来
的2倍,那么它的两个锐角的正切值( )
A.都没有变化 B.都扩大为原来的2倍
C.都缩小为原来的一半 D.不能确定是否发生变化
课堂练习
2.以下对坡度的描述正确的是( )
A.坡度是指倾斜角的度数
B.坡度是指斜坡的铅直高度与水平宽度的比
C.坡度是指斜坡的水平宽度与铅直高度的比
D.坡度是指斜坡的高度与斜坡长度的比
3.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tan A的值是( )
A. B. C. D.
4.在Rt△ABC中,CD为斜边AB上的高,且CD=2,BD=8,则tan A的值是( )
A.2 B.4 C. D.
5.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tan B的值是( )
A. B. 3 C. D.
6.如图, △ABC是等腰三角形,你能根据图中所给数据求出tanC吗?
B
C
正切:∠A的对边与邻边的比叫做∠A的正切,记作tan A, 即tan A=
A
B
C
∠A的对边a
┌
斜边c
∠A的邻边b
正切与坡度(角)的关系:坡度就是坡角的正切.
课堂小结
谢谢聆听
