人教版九年级下册数学28.1:锐角三角函数(word版,无答案)
文档属性
| 名称 | 人教版九年级下册数学28.1:锐角三角函数(word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 78.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 13:07:46 | ||
图片预览

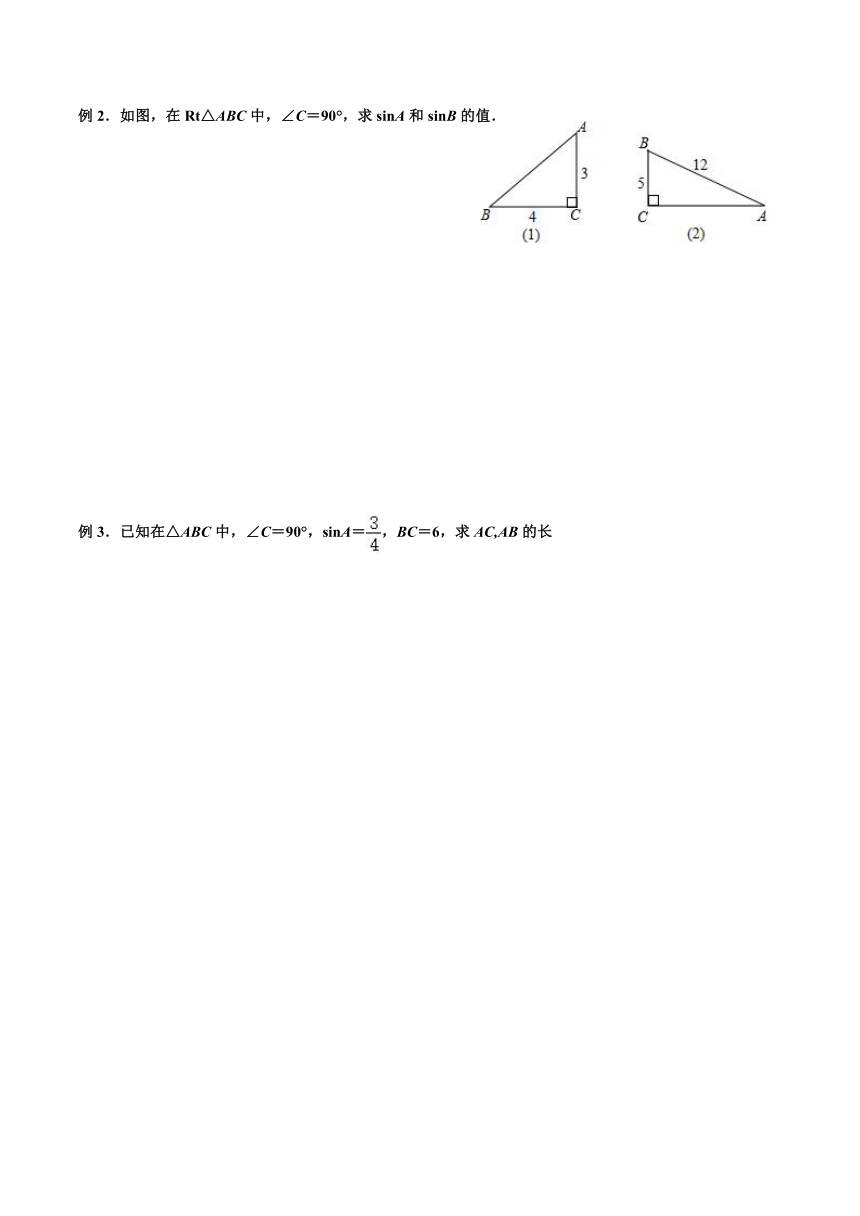


文档简介
锐角三角函数
一、在Rt△ABC中,∠C=90°.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边除以斜边=
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边除以斜边=
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边除以∠A的邻边=
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
二、特殊角的三角函数值
记忆口诀:
知识点一、三角函数定义
例1.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,AC=5,则下列三角函数表示正确的是(
)
A.sinA=
B.cosA=
C.tanA=
D.tanB=
例2.如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
例3.已知在△ABC中,∠C=90°,sinA=,BC=6,求AC,AB的长
例4.如图,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)利用此图形求tan15°的值(结果保留根号)
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线
于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
知识点二、特殊角的三角函数值
例6.在Rt△ABC中,∠C=90°,∠A=60°,则sinA+cosB的值为(
)
A.
B.
C.
D.
例7.在Rt△ABC中,AB=4,AC=2,∠C=90°,则∠A的度数为(
)
A.30°
B.40°
C.45°
D.60°
例8.在锐角△ABC中,,则∠A=(
)
A.30°
B.45°
C.60°
D.75°
例9.如图,P(12,a)在反比例函数图象上,PH⊥x轴于H,则tan∠POH的值为
.
例10.计算:
(1)2sin30°+cos60°﹣cos245°
(2)sin245°﹣2tan30°?sin60°
(3)(﹣1)0+sin45°﹣22
(4)
例11.已知a,b,c是△ABC的三边a,b,c满足等式(2b)2=4(c+a)(c﹣a),且5a﹣3c=0,
求sinA+sinB+sinC的值
【课后作业】
1.如图,△ABC中,∠B=90°,BC=2AB,则sinC=(
)
A.
B.
C.
D.
2.如图,在△ABC中,∠C=90°,AC=3,若cosA=,则BC的长为
.
3.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.
4.如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tan∠D=,
则=
.
5.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,tanB=,若BC=10,则AD的长为
.
6.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,
则tanD=
.
7.已知α为锐角,且sin(α﹣10°)=,则α等于(
)
A.70°
B.60°
C.50°
D.30°
8.cos60°﹣sin30°+tan45°的值为(
)
A.2
B.﹣2
C.1
D.﹣1
9.如图,在Rt△ABC中,∠C=90°,AB=10,tan∠A=,求BC的长和sin∠B的值.
10.已知a,b,c是△ABC的三边,a,b,c满足等式b2=(c+a)(c﹣a),且5b﹣4c=0,
求sinA+sinB的值.
一、在Rt△ABC中,∠C=90°.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边除以斜边=
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边除以斜边=
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边除以∠A的邻边=
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
二、特殊角的三角函数值
记忆口诀:
知识点一、三角函数定义
例1.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,AC=5,则下列三角函数表示正确的是(
)
A.sinA=
B.cosA=
C.tanA=
D.tanB=
例2.如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.
例3.已知在△ABC中,∠C=90°,sinA=,BC=6,求AC,AB的长
例4.如图,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)利用此图形求tan15°的值(结果保留根号)
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线
于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
知识点二、特殊角的三角函数值
例6.在Rt△ABC中,∠C=90°,∠A=60°,则sinA+cosB的值为(
)
A.
B.
C.
D.
例7.在Rt△ABC中,AB=4,AC=2,∠C=90°,则∠A的度数为(
)
A.30°
B.40°
C.45°
D.60°
例8.在锐角△ABC中,,则∠A=(
)
A.30°
B.45°
C.60°
D.75°
例9.如图,P(12,a)在反比例函数图象上,PH⊥x轴于H,则tan∠POH的值为
.
例10.计算:
(1)2sin30°+cos60°﹣cos245°
(2)sin245°﹣2tan30°?sin60°
(3)(﹣1)0+sin45°﹣22
(4)
例11.已知a,b,c是△ABC的三边a,b,c满足等式(2b)2=4(c+a)(c﹣a),且5a﹣3c=0,
求sinA+sinB+sinC的值
【课后作业】
1.如图,△ABC中,∠B=90°,BC=2AB,则sinC=(
)
A.
B.
C.
D.
2.如图,在△ABC中,∠C=90°,AC=3,若cosA=,则BC的长为
.
3.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.
4.如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tan∠D=,
则=
.
5.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,tanB=,若BC=10,则AD的长为
.
6.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,
则tanD=
.
7.已知α为锐角,且sin(α﹣10°)=,则α等于(
)
A.70°
B.60°
C.50°
D.30°
8.cos60°﹣sin30°+tan45°的值为(
)
A.2
B.﹣2
C.1
D.﹣1
9.如图,在Rt△ABC中,∠C=90°,AB=10,tan∠A=,求BC的长和sin∠B的值.
10.已知a,b,c是△ABC的三边,a,b,c满足等式b2=(c+a)(c﹣a),且5b﹣4c=0,
求sinA+sinB的值.
