人教版七年级数学下册导学案 第五章 相交线与平行线 5.1.2 垂线(第一课时)
文档属性
| 名称 | 人教版七年级数学下册导学案 第五章 相交线与平行线 5.1.2 垂线(第一课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 125.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 12:11:27 | ||
图片预览

文档简介
人教版七年级数学下册导学案
第五章
相交线与平行线
5.1.2
垂线(第一课时)
【学习目标】
1.理解垂线的概念,会用三角尺或量角器过一点画已知直线的垂线.
2.掌握垂线的性质,并会利用所学知识进行简单的推理.
【课前预习】
1.点P是直线l外一点,A为垂足,PA⊥l,且PA=5cm,则点P到直线l的距离(
)
A.小于PA=5cm
B.等于PA=5cm
C.大于PA=5cm
D.不确定
2.下列说法中,正确的是(
)
A.在同一平面内,过一点有无数条直线与已知直线垂直
B.两直线相交,对顶角互补
C.垂线段最短
D.直线外一点到这条直线的垂线段叫做点到直线的距离
3.下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
4.下列说法中,不正确的是(
)
A.两直线相交所成的四个角中有两个角相等,则这两条直线互相垂直
B.在同一平面内,经过一已知点能画一条直线和已知直线垂直
C.一条直线可以有无数条垂线
D.在同一平面内,过射线的端点与射线垂直的直线只有一条
5.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为(
)
A.4cm
B.2cm;
C.小于2cm
D.不大于2cm
6.如图所示,直线AB,CD相交于点O,于点O,OF平分,,则下列结论中不正确的是(
)
A.
B.
C.与互为补角
D.的余角等于
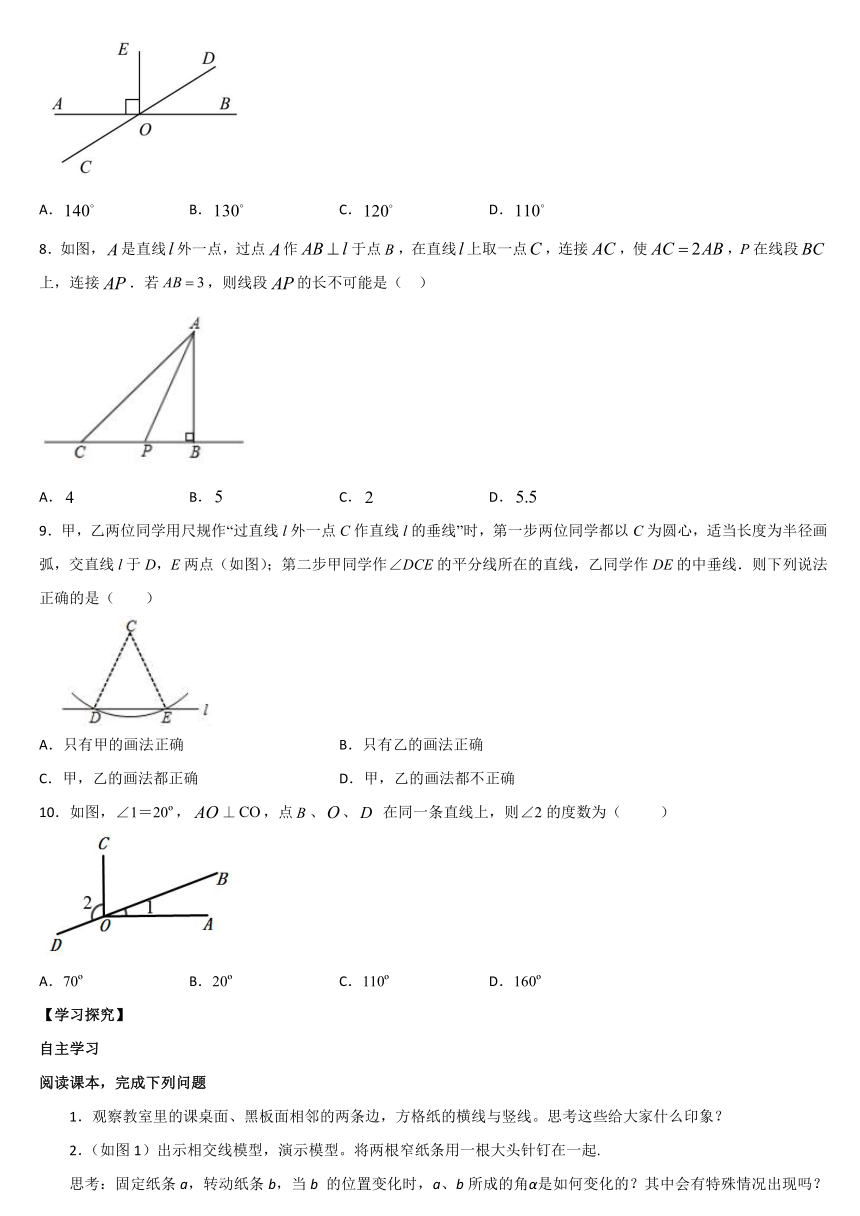
7.如图,直线AB与CD相交于点O,∠BOD=40°,OE⊥AB,则∠COE的度数为(
)
A.
B.
C.
D.
8.如图,是直线外一点,过点作于点,在直线上取一点,连接,使,P在线段上,连接.若,则线段的长不可能是(
)
A.
B.
C.
D.
9.甲,乙两位同学用尺规作“过直线l外一点C作直线l的垂线”时,第一步两位同学都以C为圆心,适当长度为半径画弧,交直线l于D,E两点(如图);第二步甲同学作∠DCE的平分线所在的直线,乙同学作DE的中垂线.则下列说法正确的是( )
A.只有甲的画法正确
B.只有乙的画法正确
C.甲,乙的画法都正确
D.甲,乙的画法都不正确
10.如图,∠1=20?,⊥,点、、
在同一条直线上,则∠2的度数为(
)
A.70?
B.20?
C.110?
D.160?
【学习探究】
自主学习
阅读课本,完成下列问题
1.观察教室里的课桌面、黑板面相邻的两条边,方格纸的横线与竖线。思考这些给大家什么印象?
2.(如图1)出示相交线模型,演示模型。将两根窄纸条用一根大头针钉在一起.
思考:固定纸条a,转动纸条b,当b
的位置变化时,a、b所成的角α是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a、b所成的四个角有什么特殊关系?
3.归纳:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相
,其中一条直线叫做另一条直线的
,它们的交点叫做
.
4.垂直用符号
来表示,如直线AB、CD互相垂直,记作:
,读作:
.
互学探究
探究(一)垂线的定义及表示
操作与思考:固定木条a,转动木条,
当b的位置变化时,a、b所成的∠a是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a、b所成的四个角有什么特殊关系?都是什么角?
结论:当b的位置变化时,∠a从锐角变为钝角,其中∠a是_____角(即:∠a=_____)时是特殊情况;其特殊之处还在于:当∠a是_____角时,它的邻补角,对顶角都是_____角,即a、b所成的四个角都是_____角,都_____度.
垂直的定义:两条直线相交,所成四个角中有一个角是_____角时,我们称这两条直线__________,其中一条直线是另一条的_____,他们的交点叫做_____。
表示方法:垂直用符号“⊥”来表示,如图,“直线AB垂直于直线CD,
垂足为O”,则记为___________________________________。
垂直的推理应用(即:几何语言):如右上图
(1)∵∠AOD=90°(
)
(2)∵
AB⊥CD
(
)
∴AB⊥CD
(
)
∴
∠AOD=90°(
)
探究(二).垂线的性质
动手操作画图:(1).用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
(2).经过直线l上一点A画l的垂线,这样的垂线能画出几条?
(3).经过直线l外一点B画l的垂线,这样的垂线能画出几条?
思考:画已知直线的垂线能画几条?经过一点(已知直线上或直线外),能画出已知直线的几条垂线?
垂线的性质
______________________。
例题
例1.(1)如图1,若直线m、n相交于点O,
∠1=90°,则______;
(2)如图2,BO⊥AO,∠BOC与∠BOA的
度数之比为1∶5,那么∠COA=____,
∠BOC的补角为______.
例2.如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求
∠AOM和∠NOC的度数.
【课后练习】
1.下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
2.下列选项中,不是运用“垂线段最短”这一性质的是( )
A.立定跳远时测量落点后端到起跳线的距离
B.从一个村庄向一条河引一条最短的水渠
C.把弯曲的公路改成直道可以缩短路程
D.直角三角形中任意一条直角边的长度都比斜边短
3.下列说法中错误的是(
)
A.一个锐角的补角一定是钝角;
B.同角或等角的余角相等;
C.两点间的距离是连结这两点的线段的长度;
D.过直线l上的一点有且只有一条直线垂直于l
4.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4
cm,PB=5
cm,PC=2
cm,则点P到直线m的距离为(
)
A.4
cm
B.5
cm
C.小于2
cm
D.不大于2
cm
5.下列命题:①两条直线相交,一角的两邻补角相等,则这两条直线垂直;②两条直线相交,一角与其邻补角相等,则这两条直线垂直;③过一点有且只有一条直线与已知直线平行;④直线外一点到这条直线的垂线段,叫做点到直线的距离.其中正确的个数为(
).
A.3
B.2
C.1
D.0
6.已知A、B为平面上的2个定点,且AB=5.若点A、B到直线l的距离分别等于2、3,则满足条件的直线共有( )条.
A.2
B.3
C.4
D.5
7.点A、B、C为直线l上三点,点P为直线l外一点,且PA=3cm,PB=4cm,PC=5cm,则点P到直线l的距离为(
)
A.2cm
B.3cm
C.小于3cm
D.不大于3cm
8.如图,学校举行运动会,A为主席台位置,对面是观众席,甲、乙、丙、丁四位同学分别坐在观众席的点B,C,D,E的位置上,已知B,C,D,E四点在一条直线上,且AD⊥BE,问距离主席台最近的同学是()
A.甲
B.乙
C.丙
D.丁
9.下列说法:①相等的角是对顶角;②平面内,过一点有且只有一条直线与已知直线垂直;③
平行于同一条直线的两条直线互相平行;
④同角或等角的余角相等,其中正确的说法有(
)
A.4
个
B.3
个
C.2
个
D.1
个
10.在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°,则∠NPB的度数是( )
A.50°
B.60°
C.40°或140°
D.50°或130°
11.过直线AB上一点O作射线OC、OD,使OC⊥OD,当∠AOC=50°时,则∠BOD的度数__.
12.运动会上裁判员测量跳远成绩时,先在距离踏板最近的跳远落地点上插上作为标记的小旗,再以小旗的位置为赤字的零点,将尺子拉直,并与踏板边缘所在直线垂直,把尺子上垂足点表示的数作为跳远成绩.这实质上是数学知识____________在生活中的应用.
13.关于垂线,小明给出了下面三种说法:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直;②这两条直线的交点叫垂足;③直线AB⊥CD,也可以说成CD⊥AB.其中正确的有______(填序号).
14.两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角.(______)
15.在直线AB上任取一点O,过点O作射线OC、OD,使∠COD=90°,当∠AOC=50°时,∠BOD的度数是____________.
【参考答案】
【课前预习】
1.B
2.C
3.C
4.A
5.D
6.D
7.B
8.C
9.C
10.C
【课后练习】
1.C
2.C
3.D
4.D
5.C
6.B
7.D
8.C
9.B
10.D
11.40?或140?
12.垂线段最短
13.①③.
14.正确
15.40°或140°
第五章
相交线与平行线
5.1.2
垂线(第一课时)
【学习目标】
1.理解垂线的概念,会用三角尺或量角器过一点画已知直线的垂线.
2.掌握垂线的性质,并会利用所学知识进行简单的推理.
【课前预习】
1.点P是直线l外一点,A为垂足,PA⊥l,且PA=5cm,则点P到直线l的距离(
)
A.小于PA=5cm
B.等于PA=5cm
C.大于PA=5cm
D.不确定
2.下列说法中,正确的是(
)
A.在同一平面内,过一点有无数条直线与已知直线垂直
B.两直线相交,对顶角互补
C.垂线段最短
D.直线外一点到这条直线的垂线段叫做点到直线的距离
3.下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
4.下列说法中,不正确的是(
)
A.两直线相交所成的四个角中有两个角相等,则这两条直线互相垂直
B.在同一平面内,经过一已知点能画一条直线和已知直线垂直
C.一条直线可以有无数条垂线
D.在同一平面内,过射线的端点与射线垂直的直线只有一条
5.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为(
)
A.4cm
B.2cm;
C.小于2cm
D.不大于2cm
6.如图所示,直线AB,CD相交于点O,于点O,OF平分,,则下列结论中不正确的是(
)
A.
B.
C.与互为补角
D.的余角等于
7.如图,直线AB与CD相交于点O,∠BOD=40°,OE⊥AB,则∠COE的度数为(
)
A.
B.
C.
D.
8.如图,是直线外一点,过点作于点,在直线上取一点,连接,使,P在线段上,连接.若,则线段的长不可能是(
)
A.
B.
C.
D.
9.甲,乙两位同学用尺规作“过直线l外一点C作直线l的垂线”时,第一步两位同学都以C为圆心,适当长度为半径画弧,交直线l于D,E两点(如图);第二步甲同学作∠DCE的平分线所在的直线,乙同学作DE的中垂线.则下列说法正确的是( )
A.只有甲的画法正确
B.只有乙的画法正确
C.甲,乙的画法都正确
D.甲,乙的画法都不正确
10.如图,∠1=20?,⊥,点、、
在同一条直线上,则∠2的度数为(
)
A.70?
B.20?
C.110?
D.160?
【学习探究】
自主学习
阅读课本,完成下列问题
1.观察教室里的课桌面、黑板面相邻的两条边,方格纸的横线与竖线。思考这些给大家什么印象?
2.(如图1)出示相交线模型,演示模型。将两根窄纸条用一根大头针钉在一起.
思考:固定纸条a,转动纸条b,当b
的位置变化时,a、b所成的角α是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a、b所成的四个角有什么特殊关系?
3.归纳:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相
,其中一条直线叫做另一条直线的
,它们的交点叫做
.
4.垂直用符号
来表示,如直线AB、CD互相垂直,记作:
,读作:
.
互学探究
探究(一)垂线的定义及表示
操作与思考:固定木条a,转动木条,
当b的位置变化时,a、b所成的∠a是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a、b所成的四个角有什么特殊关系?都是什么角?
结论:当b的位置变化时,∠a从锐角变为钝角,其中∠a是_____角(即:∠a=_____)时是特殊情况;其特殊之处还在于:当∠a是_____角时,它的邻补角,对顶角都是_____角,即a、b所成的四个角都是_____角,都_____度.
垂直的定义:两条直线相交,所成四个角中有一个角是_____角时,我们称这两条直线__________,其中一条直线是另一条的_____,他们的交点叫做_____。
表示方法:垂直用符号“⊥”来表示,如图,“直线AB垂直于直线CD,
垂足为O”,则记为___________________________________。
垂直的推理应用(即:几何语言):如右上图
(1)∵∠AOD=90°(
)
(2)∵
AB⊥CD
(
)
∴AB⊥CD
(
)
∴
∠AOD=90°(
)
探究(二).垂线的性质
动手操作画图:(1).用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
(2).经过直线l上一点A画l的垂线,这样的垂线能画出几条?
(3).经过直线l外一点B画l的垂线,这样的垂线能画出几条?
思考:画已知直线的垂线能画几条?经过一点(已知直线上或直线外),能画出已知直线的几条垂线?
垂线的性质
______________________。
例题
例1.(1)如图1,若直线m、n相交于点O,
∠1=90°,则______;
(2)如图2,BO⊥AO,∠BOC与∠BOA的
度数之比为1∶5,那么∠COA=____,
∠BOC的补角为______.
例2.如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求
∠AOM和∠NOC的度数.
【课后练习】
1.下列四个说法:①两点之间,线段最短;②连接两点之间的线段叫做这两点间的距离;③经过直线外一点,有且只有一条直线与这条直线平行;④直线外一点与这条直线上各点连接的所有线段中,垂线段最短.其中正确的个数有(
)
A.1个
B.2个
C.3个
D.4个
2.下列选项中,不是运用“垂线段最短”这一性质的是( )
A.立定跳远时测量落点后端到起跳线的距离
B.从一个村庄向一条河引一条最短的水渠
C.把弯曲的公路改成直道可以缩短路程
D.直角三角形中任意一条直角边的长度都比斜边短
3.下列说法中错误的是(
)
A.一个锐角的补角一定是钝角;
B.同角或等角的余角相等;
C.两点间的距离是连结这两点的线段的长度;
D.过直线l上的一点有且只有一条直线垂直于l
4.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4
cm,PB=5
cm,PC=2
cm,则点P到直线m的距离为(
)
A.4
cm
B.5
cm
C.小于2
cm
D.不大于2
cm
5.下列命题:①两条直线相交,一角的两邻补角相等,则这两条直线垂直;②两条直线相交,一角与其邻补角相等,则这两条直线垂直;③过一点有且只有一条直线与已知直线平行;④直线外一点到这条直线的垂线段,叫做点到直线的距离.其中正确的个数为(
).
A.3
B.2
C.1
D.0
6.已知A、B为平面上的2个定点,且AB=5.若点A、B到直线l的距离分别等于2、3,则满足条件的直线共有( )条.
A.2
B.3
C.4
D.5
7.点A、B、C为直线l上三点,点P为直线l外一点,且PA=3cm,PB=4cm,PC=5cm,则点P到直线l的距离为(
)
A.2cm
B.3cm
C.小于3cm
D.不大于3cm
8.如图,学校举行运动会,A为主席台位置,对面是观众席,甲、乙、丙、丁四位同学分别坐在观众席的点B,C,D,E的位置上,已知B,C,D,E四点在一条直线上,且AD⊥BE,问距离主席台最近的同学是()
A.甲
B.乙
C.丙
D.丁
9.下列说法:①相等的角是对顶角;②平面内,过一点有且只有一条直线与已知直线垂直;③
平行于同一条直线的两条直线互相平行;
④同角或等角的余角相等,其中正确的说法有(
)
A.4
个
B.3
个
C.2
个
D.1
个
10.在直线MN上取一点P,过点P作射线PA,PB,使PA⊥PB,当∠MPA=40°,则∠NPB的度数是( )
A.50°
B.60°
C.40°或140°
D.50°或130°
11.过直线AB上一点O作射线OC、OD,使OC⊥OD,当∠AOC=50°时,则∠BOD的度数__.
12.运动会上裁判员测量跳远成绩时,先在距离踏板最近的跳远落地点上插上作为标记的小旗,再以小旗的位置为赤字的零点,将尺子拉直,并与踏板边缘所在直线垂直,把尺子上垂足点表示的数作为跳远成绩.这实质上是数学知识____________在生活中的应用.
13.关于垂线,小明给出了下面三种说法:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直;②这两条直线的交点叫垂足;③直线AB⊥CD,也可以说成CD⊥AB.其中正确的有______(填序号).
14.两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角.(______)
15.在直线AB上任取一点O,过点O作射线OC、OD,使∠COD=90°,当∠AOC=50°时,∠BOD的度数是____________.
【参考答案】
【课前预习】
1.B
2.C
3.C
4.A
5.D
6.D
7.B
8.C
9.C
10.C
【课后练习】
1.C
2.C
3.D
4.D
5.C
6.B
7.D
8.C
9.B
10.D
11.40?或140?
12.垂线段最短
13.①③.
14.正确
15.40°或140°
