人教版七年级下册数学7.平面直角坐标系--平面直角坐标系中的图形面积解题技巧教案
文档属性
| 名称 | 人教版七年级下册数学7.平面直角坐标系--平面直角坐标系中的图形面积解题技巧教案 | 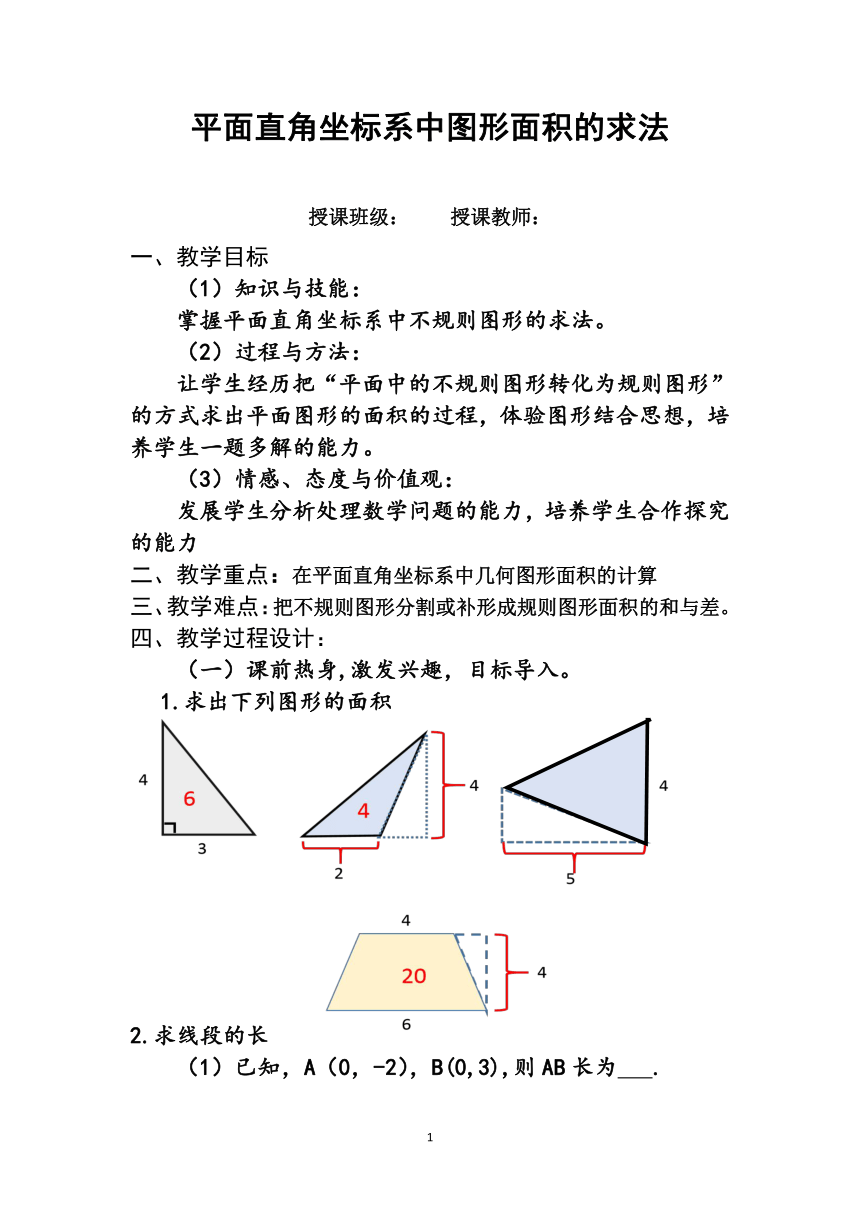 | |
| 格式 | zip | ||
| 文件大小 | 359.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 12:14:36 | ||
图片预览

文档简介
平面直角坐标系中图形面积的求法
授课班级:
授课教师:
一、教学目标?
(1)知识与技能:?
掌握平面直角坐标系中不规则图形的求法。
(2)过程与方法:?
让学生经历把“平面中的不规则图形转化为规则图形”的方式求出平面图形的面积的过程,体验图形结合思想,培养学生一题多解的能力。
情感、态度与价值观:?
发展学生分析处理数学问题的能力,培养学生合作探究的能力
二、教学重点:在平面直角坐标系中几何图形面积的计算?
三、教学难点:把不规则图形分割或补形成规则图形面积的和与差。
四、教学过程设计:?
(一)课前热身,激发兴趣,目标导入。
1.求出下列图形的面积
2.求线段的长
(1)已知,A(0,-2),B(0,3),则AB长为
.
(2)已知,A(-3,0),B(2,0),则AB长为
.
(3)已知,A(2,6),B(2,1)则AB长为
。
(二)自学自研(完成导学案)
交流展示
1、交流:对学、合学、讨论或请教老师解决疑难问题,形成本小组统一的答案。
2、展示:分组进行展示导学案的以下内容:
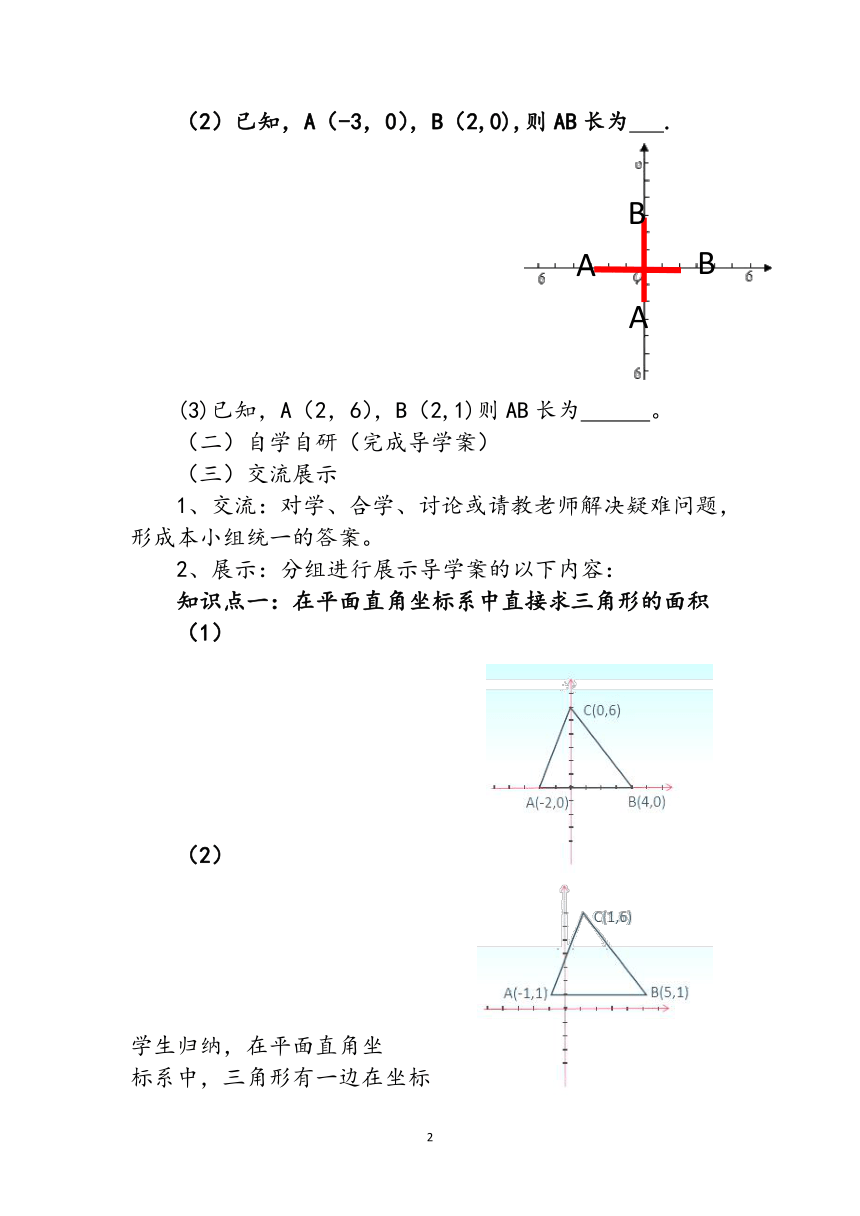
知识点一:在平面直角坐标系中直接求三角形的面积
(1)
(2)
学生归纳,在平面直角坐
标系中,三角形有一边在坐标
轴上(或平行于坐标轴),应选取坐标轴上的边(或平行于坐标轴上的边)作为三角形的底
知识点二:在平面直角坐标系中用分割法求三角形的面积
如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为________.
知识点三:在平面直角坐标系中用补形法求三角形的面积
在三角形ABC中,A、B、C三点坐标分别为A(-1,-2),B(6,2),C(1,3)
求三角形ABC的面积。
(四)课堂总结归纳:(略)?
(五)、巩固练习、作业:
练习:判断正误
如图,已知A(-2,0),
B(4,0),C(-4,4),则三角形
ABC的面积为(
).
(2)如图,已知A(-1,1),B(5,1),C(1,6),则三角形ABC的面积为(
).
作业:
1.观察右图,图中每个小正方形的边长均为1,
回答以下问题:
(1)写出多边形ABCDEF各个顶点的坐标;
(2)线段BC,CE的位置各有什么特点?
(3)求多边形ABCDEF的面积.
2.已知点A(3,4),B(-1,0),C(4,-2),
求三角形ABC的面积.
授课班级:
授课教师:
一、教学目标?
(1)知识与技能:?
掌握平面直角坐标系中不规则图形的求法。
(2)过程与方法:?
让学生经历把“平面中的不规则图形转化为规则图形”的方式求出平面图形的面积的过程,体验图形结合思想,培养学生一题多解的能力。
情感、态度与价值观:?
发展学生分析处理数学问题的能力,培养学生合作探究的能力
二、教学重点:在平面直角坐标系中几何图形面积的计算?
三、教学难点:把不规则图形分割或补形成规则图形面积的和与差。
四、教学过程设计:?
(一)课前热身,激发兴趣,目标导入。
1.求出下列图形的面积
2.求线段的长
(1)已知,A(0,-2),B(0,3),则AB长为
.
(2)已知,A(-3,0),B(2,0),则AB长为
.
(3)已知,A(2,6),B(2,1)则AB长为
。
(二)自学自研(完成导学案)
交流展示
1、交流:对学、合学、讨论或请教老师解决疑难问题,形成本小组统一的答案。
2、展示:分组进行展示导学案的以下内容:
知识点一:在平面直角坐标系中直接求三角形的面积
(1)
(2)
学生归纳,在平面直角坐
标系中,三角形有一边在坐标
轴上(或平行于坐标轴),应选取坐标轴上的边(或平行于坐标轴上的边)作为三角形的底
知识点二:在平面直角坐标系中用分割法求三角形的面积
如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为________.
知识点三:在平面直角坐标系中用补形法求三角形的面积
在三角形ABC中,A、B、C三点坐标分别为A(-1,-2),B(6,2),C(1,3)
求三角形ABC的面积。
(四)课堂总结归纳:(略)?
(五)、巩固练习、作业:
练习:判断正误
如图,已知A(-2,0),
B(4,0),C(-4,4),则三角形
ABC的面积为(
).
(2)如图,已知A(-1,1),B(5,1),C(1,6),则三角形ABC的面积为(
).
作业:
1.观察右图,图中每个小正方形的边长均为1,
回答以下问题:
(1)写出多边形ABCDEF各个顶点的坐标;
(2)线段BC,CE的位置各有什么特点?
(3)求多边形ABCDEF的面积.
2.已知点A(3,4),B(-1,0),C(4,-2),
求三角形ABC的面积.
