2020-2021学年苏科版七年级数学下册7.2平行线的性质自主学习同步测评2(Word版 附答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册7.2平行线的性质自主学习同步测评2(Word版 附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 311.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 19:24:44 | ||
图片预览


文档简介
2021年苏科新版七年级数学下册7.2平行线的性质自主学习同步测评2(附答案)
1.如图,AB⊥AE于点A,AB∥CD,∠CAE=42°,则∠ACD=( )
A.112°
B.122°
C.132°
D.142°
2.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90°
B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180°
D.∠α+∠β+∠γ=180°
3.如图,将三角尺的直角顶点放在直尺的一边上,若∠1=60°15′,则∠2的大小为( )
A.60°15′
B.39°45′
C.29°85′
D.29°45′
4.将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=62°,则∠2的度数为( )
A.28°
B.30°
C.38°
D.62°
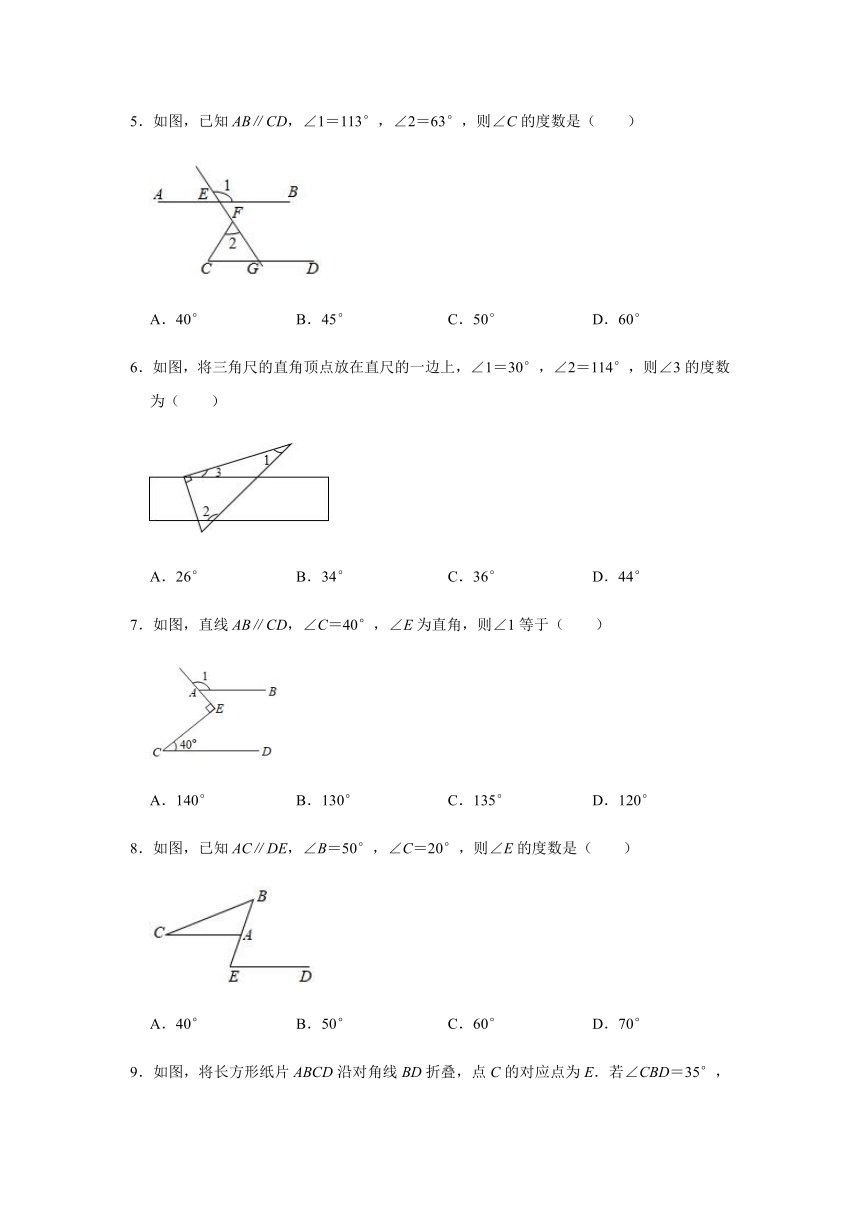
5.如图,已知AB∥CD,∠1=113°,∠2=63°,则∠C的度数是( )
A.40°
B.45°
C.50°
D.60°
6.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=114°,则∠3的度数为( )
A.26°
B.34°
C.36°
D.44°
7.如图,直线AB∥CD,∠C=40°,∠E为直角,则∠1等于( )
A.140°
B.130°
C.135°
D.120°
8.如图,已知AC∥DE,∠B=50°,∠C=20°,则∠E的度数是( )
A.40°
B.50°
C.60°
D.70°
9.如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为E.若∠CBD=35°,则∠ADE的度数为( )
A.15°
B.20°
C.25°
D.30°
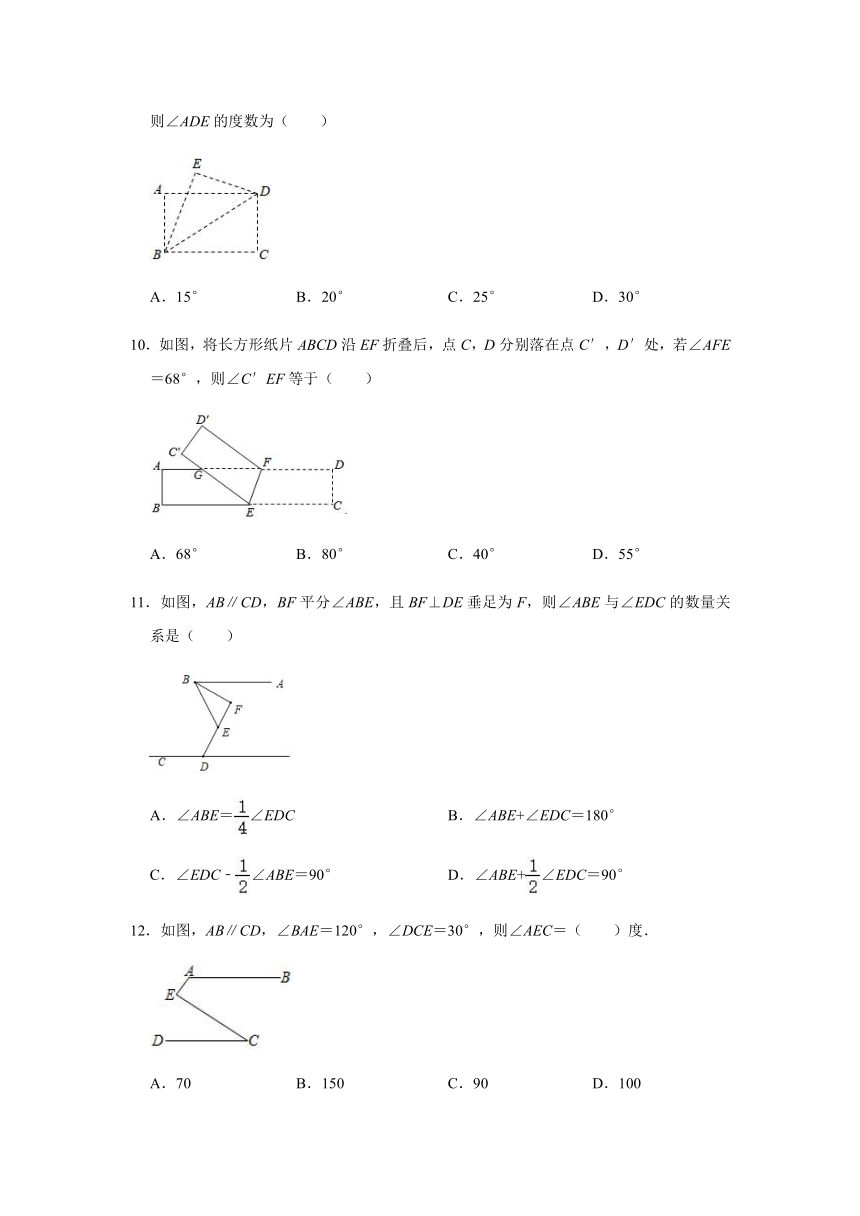
10.如图,将长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′处,若∠AFE=68°,则∠C′EF等于( )
A.68°
B.80°
C.40°
D.55°
11.如图,AB∥CD,BF平分∠ABE,且BF⊥DE垂足为F,则∠ABE与∠EDC的数量关系是( )
A.∠ABE=∠EDC
B.∠ABE+∠EDC=180°
C.∠EDC﹣∠ABE=90°
D.∠ABE+∠EDC=90°
12.如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.
A.70
B.150
C.90
D.100
13.如图,∠DAC+∠ACB=180°,EF∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是( )
A.10°
B.20°
C.15°
D.30°
14.如图,l1∥l2,则∠1、∠2、∠3关系是( )
A.∠2>∠1+∠3
B.无法确定
C.∠3=∠1﹣∠2
D.∠2=∠1+∠3
15.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2
B.∠1+∠2
C.∠2﹣∠1
D.180°+∠2﹣2∠1
16.将一副三角板的直角顶点重合按如图放置,小明得到下列结论:
①如果∠2=30°,则AC∥DE;②∠BAE+∠CAD=180°;
③如果BC∥AD,则∠2=30°;④如果∠CAD=150°,则∠4=∠C.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
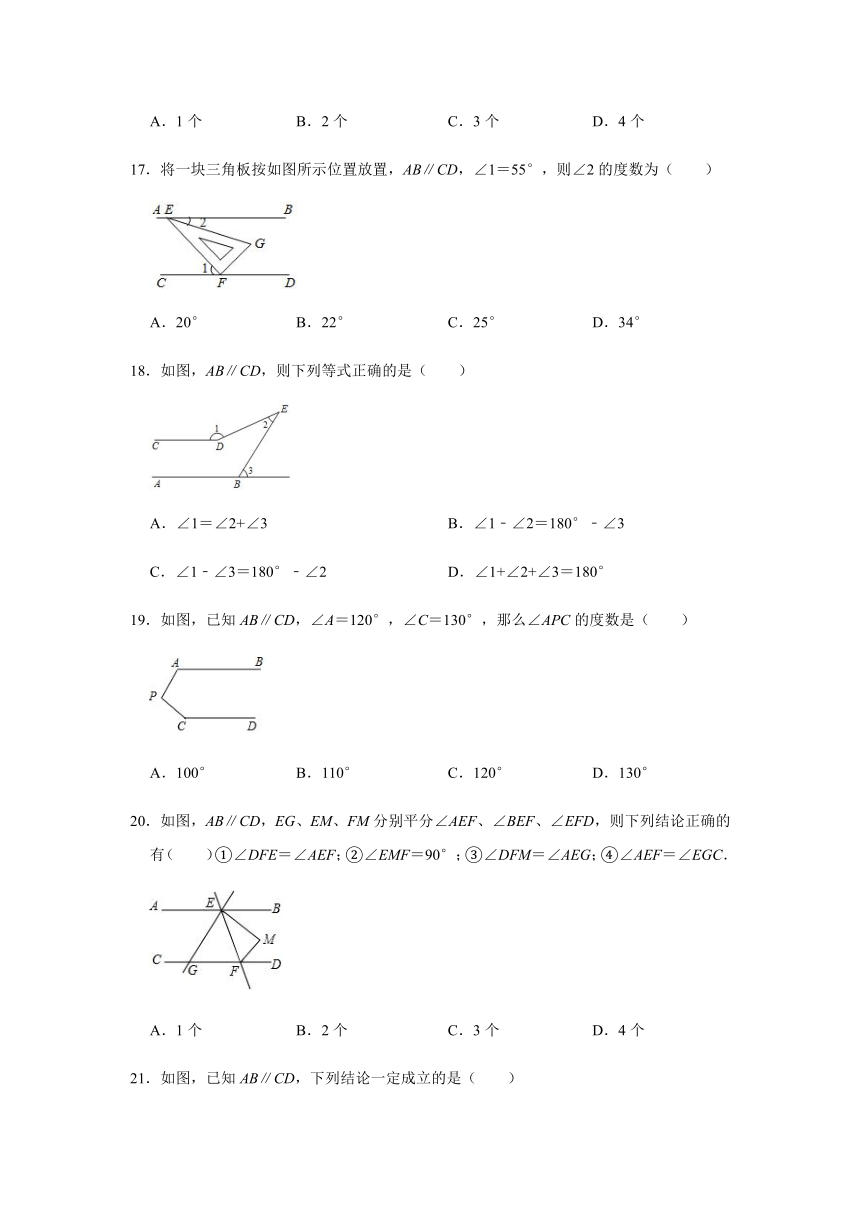
17.将一块三角板按如图所示位置放置,AB∥CD,∠1=55°,则∠2的度数为( )
A.20°
B.22°
C.25°
D.34°
18.如图,AB∥CD,则下列等式正确的是( )
A.∠1=∠2+∠3
B.∠1﹣∠2=180°﹣∠3
C.∠1﹣∠3=180°﹣∠2
D.∠1+∠2+∠3=180°
19.如图,已知AB∥CD,∠A=120°,∠C=130°,那么∠APC的度数是( )
A.100°
B.110°
C.120°
D.130°
20.如图,AB∥CD,EG、EM、FM分别平分∠AEF、∠BEF、∠EFD,则下列结论正确的有( )①∠DFE=∠AEF;②∠EMF=90°;③∠DFM=∠AEG;④∠AEF=∠EGC.
A.1个
B.2个
C.3个
D.4个
21.如图,已知AB∥CD,下列结论一定成立的是( )
A.∠A=∠C
B.∠C=∠E
C.∠A﹣∠C=∠E
D.∠C=∠A+∠E
22.如图,AE∥BD,∠1=115°,∠2=40°,则∠C的度数是( )
A.15°
B.25°
C.35°
D.45°
23.如图,直线l1∥l2,点A在l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点;连接AC,BC.若∠ABC=55°,则∠1的大小为
.
24.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD=
.
25.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于
.
26.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连结PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为
度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
27.如图,AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC平分∠ABP交AM于点C,BD平分∠PBN交AM于点D.
(1)求∠ABN的度数.
(2)求∠CBD的度数.
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若变化,请写出变化规律;若不变化,请写出它们之间的数量关系,并说明理由.
28.已知点A在射线CE上,∠BDA=∠C.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请证明∠DAE+2∠C=90°;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线CE于点F,当∠DFE=8∠DAE时,求∠BAD的度数.(直接写出结果)
29.完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED(
)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(
)
∴DF∥AE(
)
∴∠EGF+∠AEG=180°(
)
30.几何说理填空:如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2,求证:DE∥BC.
证明:连接EF
∵FG⊥AC,HE⊥AC,
∴∠FGC=∠HEC=90°(
).
∴
∥
(
).
∴∠3=∠
(
).
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4.
即∠DEF=∠EFC
∴DE∥BC(
).
31.完成下面推理过程.
如图:已知,∠A=112°,∠ABC=68°,BD⊥DC于点D,EF⊥DC于点F,求证:∠1=∠2.
证明:∵∠A=112°,∠ABC=68°(已知)
∴∠A+∠ABC=180°
∴AD∥BC(
)
∴∠1=
(
)
∵BD⊥DC,EF⊥DC(已知)
∴∠BDF=90°,∠EFC=90°(
)
∴∠BDF=∠EFC=90°
∴BD∥EF(
)
∴∠2=
(
)
∴∠1=∠2(
)
32.如图1,AB∥CD,∠PAB=125°,∠PCD=115°,求∠APC的度数.
小明的思路是:过P作PM∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为
度;
(2)如图2,AB∥CD,点P在直线a上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点B、D两点不重合),请直接写出∠APC与α、β之间的数量关系
33.直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点.
(1)若点P在直线CD上,如图①,∠α=50°,则∠2=
°.
(2)若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;
(3)若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由.
34.(1)问题情境:如图1,AB∥CD,∠PAB=120°,∠PCD=130°,求∠APC的度数.
小辰的思路是:如图2,过点P作PE∥AB,通过平行线的性质,可求得∠APC的度数.请写出具体求解过程.
(2)问题迁移:
①如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,设∠CPD=∠α,∠ADP=∠β,∠BCP=∠γ,问:∠α、∠β、∠γ之间有何数量关系?请说明理由.
②在①的条件下,如果点P不在A、B两点之间运动时(点P与点A、B、O三点不重合),请你直接写出∠α、∠β、∠γ间的数量关系.
参考答案
1.解:∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°﹣42°=48°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故选:C.
2.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
3.解:如图,
由直尺两边平行,可得:∠1=∠3=60°15',
∴∠2=90°﹣∠3=90°﹣60°15'=29°45',
故选:D.
4.解:如图,
∵a∥b,
∴∠1=∠3=62°,
∵∠2+∠3=90°,
∴∠2=90°﹣∠3=90°﹣62°=28°,
故选:A.
5.解:∵AB∥CD,
∴∠1=∠FGD=113°,
∴∠C=∠FGD﹣∠2=113°﹣63°=50°,
故选:C.
6.解:∵AB∥CD,
∴∠ABE=∠2=114°,
在△ABE中,∠3=180°﹣∠1﹣∠ABE=180°﹣30°﹣114°=36°.
故选:C.
7.解:延长CE交AB于点F,如右图所示,
∵AB∥CD,∠C=40°,
∴∠C=∠2=40°,
∵∠AEF=90°,
∴∠1=∠AEF+∠2=90°+40°=130°,
故选:B.
8.解:∵∠B=50°,∠C=20°,
∴∠CAE=∠B+∠C=70°,
∵AC∥DE,
∴∠CAE=∠E,
∴∠E=70°,
故选:D.
9.解:由折叠的性质可得,
∠CDB=∠EDB,
∵AD∥BC,∠CBD=35°,
∴∠CBD=∠ADB=35°,
∵∠C=90°,
∴∠CDB=55°,
∴∠EDB=55°,
∴∠ADE=∠EDB﹣∠ADB=55°﹣35°=20°,
故选:B.
10.解:∵∠AFE=68°,AD∥BC,
∴∠AFE=∠CEF=68°,
由折叠的性质可得,
∠CEF=∠C′EF,
∴∠C′EF=68°,
故选:A.
11.解:过F点作FG∥AB,
∵AB∥CD,
∴FG∥CD,
∴∠BFG=∠ABF,∠DFG+∠CDF=180°,
∵BF⊥DE,
∴∠BFD=90°,
∵BF平分∠ABE,
∴∠ABE=2∠ABF,
∴∠BFG+∠DFG+∠CDF=∠ABF+180°,
∴90°+∠CDE=∠ABE+180°,即∠EDC﹣∠ABE=90°.
故选:C.
12.解:如图,延长AE交CD于点F,
∵AB∥CD,
∴∠BAE+∠EFC=180°,
又∵∠BAE=120°,
∴∠EFC=180°﹣∠BAE=180°﹣120°=60°,
又∵∠DCE=30°,
∴∠AEC=∠DCE+∠EFC=30°+60°=90°.
故选:C.
13.解:设∠BCE=∠ECF=∠BCF=x,
∵∠DAC=3∠BCF,
∴∠DAC=6x,
∵∠DAC+∠ACB=180°,
∴6x+x+x+20°=180°,
解得x=20°,
所以,∠FEC的度数为20°.
故选:B.
14.解:过∠2的顶点,作如图所示的射线l,使l∥l1,
∵l1∥l2,l∥l1,
∴l1∥l2∥l.
∴∠1=∠α,∠2=∠β.
∵∠α+∠β=∠2,
∴∠1+∠3=∠2.
故选:D.
15.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
16.解:∵∠2=30°,∠CAB=90°,
∴∠1=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE,故①正确;
∵∠CAB=∠DAE=90°,
∴∠BAE+∠CAD=90°﹣∠1+90°+∠1=180°,故②正确;
∵BC∥AD,∠B=45°,
∴∠3=∠B=45°,
∵∠2+∠3=∠DAE=90°,
∴∠2=45°,故③错误;
∵∠CAD=150°,∠BAE+∠CAD=180°,
∴∠BAE=30°,
∵∠E=60°,
∴∠BOE=∠BAE+∠E=90°,
∴∠4+∠B=90°,
∵∠B=45°,
∴∠4=45°,
∵∠C=45°,
∴∠4=∠C,故④正确;
所以其中正确的结论有①②④,3个.
故选:C.
17.解:过G作直线MN∥AB,如下图所示,
∵MN∥AB,
∴∠2=∠3(两直线平行,内错角相等),
∵MN∥AB,AB∥CD,
∴MN∥CD,
∴∠5=∠4(两直线平行,内错角相等),
∴∠EGF=∠3+∠5=∠2+∠4=60°,
∵∠EFG=90°,
∴∠1+∠4=180°﹣90°=90°,
∴∠2=60°﹣∠4=60°﹣(90°﹣∠1)=∠1﹣30°=55°﹣30°=25°,
故选:C.
18.解:如右图所示,
∵CD∥AB,
∴∠4=∠3,
∵∠4=∠2+(180°﹣∠1),
∴∠3=∠2+(180°﹣∠1),
∴∠1﹣∠2=180°﹣∠3,
故选:B.
19.解:过P作直线MN∥AB,如下图所示,
∵MN∥AB,
∴∠A+∠1=180°(两直线平行,同旁内角互补),
∴∠1=180°﹣∠A=180°﹣120°=60°,
∵MN∥AB,AB∥CD,
∴MN∥CD,
∴∠C+∠2=180°(两直线平行,同旁内角互补),
∴∠2=180°﹣∠C=180°﹣130°=50°,
∴∠APC=∠1+∠2=60°+50°=110°,
故选:B.
20.解:如下图所示,
①∵AB∥CD,
∴∠DFE=∠AEF(两直线平行,内错角相等),
故①正确;
②∵EM平分∠BEF,
∴∠3=∠4,
∵FM平分∠EFD,
∴∠5=∠6,
∵AB∥CD,
∴∠3+∠4+∠5+∠6=180°(两直线平行,同旁内角互补),
∴∠3+∠5=90°,
∴∠EMF=180°﹣∠3﹣∠5=180°﹣90°=90°,
故②正确;
③∵AB∥CD,
∴∠1+∠2=∠5+∠6(两直线平行,内错角相等),
∵EG平分∠AEF,
∵∠1=∠2,
∵FM平分∠EFD,
∴∠5=∠6,
∴∠1=∠6,
∴∠DFM=∠AEG,
故③正确;
④由题意得∠AEF=∠1+∠2,∠EGC=∠2+∠EFG,
∵根据题意无法判断∠1与∠EFG的大小关系,
∴∠AEF不一定等于∠EFG,
故④不正确;
综上所述,正确的结论有3个,
故选:C.
21.解:设AE与CD相交于M点,如下图所示,
A.∵AB∥CD,
∴∠A=∠AMC(两直线平行,内错角相等),
∵∠AMC=∠C+∠E(外角的性质),
∴∠AMC>∠C,
∴∠A>∠C,
故A选项不符合题意;
B.由题意得无法根据AB∥CD得出∠C与∠E的关系,故B选项不符合题意;
C.∵AB∥CD,
∴∠A=∠AMC(两直线平行,内错角相等),
∵∠AMC=∠C+∠E(外角的性质),
∴∠A=∠C+∠E,
故C选项符合题意;
D.∵AB∥CD,
∴∠A=∠AMC(两直线平行,内错角相等),
∵∠AMC=∠C+∠E(外角的性质),
∴∠AMC>∠C,
∴∠A>∠C,
∴∠C<∠A+∠E
∴故D选项不符合题意;
故选:C.
22.解:∵AE∥BD,∠2=40°,
∴∠CEA=∠2=40°,
又∵∠1=115°,
∴∠C=180°﹣∠CEA﹣∠1=180°﹣115°﹣40°=25°.
故选:B.
23.解:∵AC=AB,
∴∠ACB=∠ABC=55°,
根据三角形的内角和定理得:∠ACB+∠ABC+∠CAB=180°,
∴∠CAB=180°﹣∠ACB﹣∠ABC=180°﹣55°﹣55°=70°,
∵l1∥l2,
∴∠1=∠CAB=70°,
故答案为:70°.
24.解:∵AB∥CD,
∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,
∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠1+∠3=45°,
∵∠5=∠2+∠3,
∴∠5=∠1+∠3=45°,
即∠BFD=45°,
故答案为:45°.
25.解:∵AB∥CD,
∴∠FGB+∠GFD=180°,
∴∠GFD=180°﹣∠FGB=26°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=52°,
∵AB∥CD,
∴∠AEF=∠EFD=52°.
故答案为:52°.
26.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
27.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°﹣∠A=180°﹣60°=120°.
(2)∵BC平分∠ABP,BD平分∠PBN,
∴∠CBP=∠ABP,∠PBD=∠PBN,
∴∠CBD=∠CBP+∠PBD=∠ABP+∠PBN=∠ABN=60°.
(3)不变,∠APB=2∠ADB,理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PDN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB.
28.(1)证明:∵AC∥BD,
∴∠DAE=∠BDA,
∵∠BDA=∠C,
∴∠DAE=∠C,
∴AD∥BC;
(2)证明:如图2,设CE与BD相交于点G,∠BGA=∠BDA+DAE,
∵BD⊥BC,
∴∠BGA+∠C=90°,
∴∠BDA+∠DAE+∠C=90°,
∵∠BDA=∠C,
∴∠DAE+2∠C=90°;
(3)如图3,设∠DAE=α,则∠DFE=8α,
∵∠DFE+∠AFD=180°,
∴∠AFD=180°﹣8α,
∵DF∥BC,
∴∠C=∠AFD=180°﹣8α,
又∵2∠C+∠DAE=90°,
∴2(180°﹣8α)+α=90°,
∴α=18°,
∴∠C=180°﹣8α=36°=∠ADB,
又∵∠C=∠BDA,∠BAC=∠BAD,
∴∠ABC=∠ABD=∠CBD=45°,
△ABD中,∠BAD=180°﹣45°﹣36°=99°.
答:∠BAD的度数是99°.
29.证明:∵DE∥AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF∥AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
30.证明:连接EF
∵FG⊥AC,HE⊥AC,
∴∠FGC=∠HEC=90°(垂线的性质).
∴FG∥HE(同位角相等,两直线平行).
∴∠3=∠4(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4.
即∠DEF=∠EFC
∴DE∥BC(内错角相等,两直线平行).
故答案为:垂线的性质;FG,HE,同位角相等,两直线平行;4,两直线平行,内错角相等;内错角相等,两直线平行.
31.证明:∵∠A=112°,∠ABC=68°(已知),
∴∠A+∠ABC=180°.
∴AD∥BC(同旁内角互补,两直线平行).
∴∠1=∠3
(两直线平行,内错角相等
).
∵BD⊥DC,EF⊥DC(已知),
∴∠BDF=90°,∠EFC=90°(垂直的定义).
∴∠BDF=∠EFC=90°.
∴BD∥EF(同位角相等,两直线平行).
∴∠2=∠3(两直线平行,同位角相等).
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;∠3;两直线平行,内错角相等;垂直的定义;
同位角相等,两直线平行;∠3;两直线平行,同位角相等;等量代换.
32.解:(1)如图1,过P作PM∥AB,
∴∠APM+∠PAB=180°,
∴∠APM=180°﹣125°=55°,
∵AB∥CD,
∴PM∥CD,
∴∠CPM+∠PCD=180°,
∴∠CPM=180°﹣115°=65°,
∴∠APC=55°+65°=120°;
故答案为:120;
(2)如图2,∠APC=∠α+∠β,理由如下:
过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图3,当P在BD延长线时,∠APC=∠α﹣∠β;理由:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE﹣∠CPE=∠α﹣∠β;
如图4,当P在DB延长线时,∠APC=∠β﹣∠α;理由:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠CPE﹣∠APE=∠β﹣∠α;
33.解:①∵AB∥CD,∠α=50°
∴∠2=∠α=50°,
故答案为50;
(2)∠α=∠1+∠2.
证明:过P作PG∥AB,
∵AB∥CD,
∴PG∥AB∥CD,
∴∠2=∠EPG,∠1=∠FPG,
∵∠α=∠EPF=∠EPG+∠FPG,
∴∠α=∠1+∠2;
(3)不成立.
理由:过P作PH∥AB,
∵AB∥CD,
∴PH∥AB∥CD,
∴∠2=∠EPH,∠1=∠FPH,
∵∠α=∠EPF=∠EPH﹣∠FPH,
∴∠α=∠2﹣∠1,
故不成立.
34.解:(1)∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=120°,∠PCD=130°,
∴∠APE=60°,∠CPE=50°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)①当点P在A、B两点之间,如图3,作PQ∥AD,
∵PQ∥AD,AD∥BC,
∴PQ∥AD∥BC,
∴∠DPQ=∠β,∠CPQ=∠γ,
∵∠CPD=∠DPQ+∠CPQ,
∴∠α=∠β+∠γ;
②当点P在B、O两点之间时,作PQ∥AD,
∵PQ∥AD,AD∥BC,
∴PQ∥AD∥BC,
∴∠DPQ=∠β,∠CPQ=∠γ,
∵∠CPD=∠DPQ﹣∠CPQ,
∴∠α=∠β﹣∠γ
1.如图,AB⊥AE于点A,AB∥CD,∠CAE=42°,则∠ACD=( )
A.112°
B.122°
C.132°
D.142°
2.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90°
B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180°
D.∠α+∠β+∠γ=180°
3.如图,将三角尺的直角顶点放在直尺的一边上,若∠1=60°15′,则∠2的大小为( )
A.60°15′
B.39°45′
C.29°85′
D.29°45′
4.将一块直角三角尺ABC按如图所示的方式放置,其中点A、C分别落在直线a、b上,若a∥b,∠1=62°,则∠2的度数为( )
A.28°
B.30°
C.38°
D.62°
5.如图,已知AB∥CD,∠1=113°,∠2=63°,则∠C的度数是( )
A.40°
B.45°
C.50°
D.60°
6.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=114°,则∠3的度数为( )
A.26°
B.34°
C.36°
D.44°
7.如图,直线AB∥CD,∠C=40°,∠E为直角,则∠1等于( )
A.140°
B.130°
C.135°
D.120°
8.如图,已知AC∥DE,∠B=50°,∠C=20°,则∠E的度数是( )
A.40°
B.50°
C.60°
D.70°
9.如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为E.若∠CBD=35°,则∠ADE的度数为( )
A.15°
B.20°
C.25°
D.30°
10.如图,将长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′处,若∠AFE=68°,则∠C′EF等于( )
A.68°
B.80°
C.40°
D.55°
11.如图,AB∥CD,BF平分∠ABE,且BF⊥DE垂足为F,则∠ABE与∠EDC的数量关系是( )
A.∠ABE=∠EDC
B.∠ABE+∠EDC=180°
C.∠EDC﹣∠ABE=90°
D.∠ABE+∠EDC=90°
12.如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.
A.70
B.150
C.90
D.100
13.如图,∠DAC+∠ACB=180°,EF∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是( )
A.10°
B.20°
C.15°
D.30°
14.如图,l1∥l2,则∠1、∠2、∠3关系是( )
A.∠2>∠1+∠3
B.无法确定
C.∠3=∠1﹣∠2
D.∠2=∠1+∠3
15.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2
B.∠1+∠2
C.∠2﹣∠1
D.180°+∠2﹣2∠1
16.将一副三角板的直角顶点重合按如图放置,小明得到下列结论:
①如果∠2=30°,则AC∥DE;②∠BAE+∠CAD=180°;
③如果BC∥AD,则∠2=30°;④如果∠CAD=150°,则∠4=∠C.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
17.将一块三角板按如图所示位置放置,AB∥CD,∠1=55°,则∠2的度数为( )
A.20°
B.22°
C.25°
D.34°
18.如图,AB∥CD,则下列等式正确的是( )
A.∠1=∠2+∠3
B.∠1﹣∠2=180°﹣∠3
C.∠1﹣∠3=180°﹣∠2
D.∠1+∠2+∠3=180°
19.如图,已知AB∥CD,∠A=120°,∠C=130°,那么∠APC的度数是( )
A.100°
B.110°
C.120°
D.130°
20.如图,AB∥CD,EG、EM、FM分别平分∠AEF、∠BEF、∠EFD,则下列结论正确的有( )①∠DFE=∠AEF;②∠EMF=90°;③∠DFM=∠AEG;④∠AEF=∠EGC.
A.1个
B.2个
C.3个
D.4个
21.如图,已知AB∥CD,下列结论一定成立的是( )
A.∠A=∠C
B.∠C=∠E
C.∠A﹣∠C=∠E
D.∠C=∠A+∠E
22.如图,AE∥BD,∠1=115°,∠2=40°,则∠C的度数是( )
A.15°
B.25°
C.35°
D.45°
23.如图,直线l1∥l2,点A在l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点;连接AC,BC.若∠ABC=55°,则∠1的大小为
.
24.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD=
.
25.如图,AB∥CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于
.
26.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连结PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为
度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
27.如图,AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC平分∠ABP交AM于点C,BD平分∠PBN交AM于点D.
(1)求∠ABN的度数.
(2)求∠CBD的度数.
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若变化,请写出变化规律;若不变化,请写出它们之间的数量关系,并说明理由.
28.已知点A在射线CE上,∠BDA=∠C.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请证明∠DAE+2∠C=90°;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线CE于点F,当∠DFE=8∠DAE时,求∠BAD的度数.(直接写出结果)
29.完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED(
)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(
)
∴DF∥AE(
)
∴∠EGF+∠AEG=180°(
)
30.几何说理填空:如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2,求证:DE∥BC.
证明:连接EF
∵FG⊥AC,HE⊥AC,
∴∠FGC=∠HEC=90°(
).
∴
∥
(
).
∴∠3=∠
(
).
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4.
即∠DEF=∠EFC
∴DE∥BC(
).
31.完成下面推理过程.
如图:已知,∠A=112°,∠ABC=68°,BD⊥DC于点D,EF⊥DC于点F,求证:∠1=∠2.
证明:∵∠A=112°,∠ABC=68°(已知)
∴∠A+∠ABC=180°
∴AD∥BC(
)
∴∠1=
(
)
∵BD⊥DC,EF⊥DC(已知)
∴∠BDF=90°,∠EFC=90°(
)
∴∠BDF=∠EFC=90°
∴BD∥EF(
)
∴∠2=
(
)
∴∠1=∠2(
)
32.如图1,AB∥CD,∠PAB=125°,∠PCD=115°,求∠APC的度数.
小明的思路是:过P作PM∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为
度;
(2)如图2,AB∥CD,点P在直线a上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点B、D两点不重合),请直接写出∠APC与α、β之间的数量关系
33.直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点.
(1)若点P在直线CD上,如图①,∠α=50°,则∠2=
°.
(2)若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;
(3)若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由.
34.(1)问题情境:如图1,AB∥CD,∠PAB=120°,∠PCD=130°,求∠APC的度数.
小辰的思路是:如图2,过点P作PE∥AB,通过平行线的性质,可求得∠APC的度数.请写出具体求解过程.
(2)问题迁移:
①如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,设∠CPD=∠α,∠ADP=∠β,∠BCP=∠γ,问:∠α、∠β、∠γ之间有何数量关系?请说明理由.
②在①的条件下,如果点P不在A、B两点之间运动时(点P与点A、B、O三点不重合),请你直接写出∠α、∠β、∠γ间的数量关系.
参考答案
1.解:∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°﹣42°=48°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故选:C.
2.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
3.解:如图,
由直尺两边平行,可得:∠1=∠3=60°15',
∴∠2=90°﹣∠3=90°﹣60°15'=29°45',
故选:D.
4.解:如图,
∵a∥b,
∴∠1=∠3=62°,
∵∠2+∠3=90°,
∴∠2=90°﹣∠3=90°﹣62°=28°,
故选:A.
5.解:∵AB∥CD,
∴∠1=∠FGD=113°,
∴∠C=∠FGD﹣∠2=113°﹣63°=50°,
故选:C.
6.解:∵AB∥CD,
∴∠ABE=∠2=114°,
在△ABE中,∠3=180°﹣∠1﹣∠ABE=180°﹣30°﹣114°=36°.
故选:C.
7.解:延长CE交AB于点F,如右图所示,
∵AB∥CD,∠C=40°,
∴∠C=∠2=40°,
∵∠AEF=90°,
∴∠1=∠AEF+∠2=90°+40°=130°,
故选:B.
8.解:∵∠B=50°,∠C=20°,
∴∠CAE=∠B+∠C=70°,
∵AC∥DE,
∴∠CAE=∠E,
∴∠E=70°,
故选:D.
9.解:由折叠的性质可得,
∠CDB=∠EDB,
∵AD∥BC,∠CBD=35°,
∴∠CBD=∠ADB=35°,
∵∠C=90°,
∴∠CDB=55°,
∴∠EDB=55°,
∴∠ADE=∠EDB﹣∠ADB=55°﹣35°=20°,
故选:B.
10.解:∵∠AFE=68°,AD∥BC,
∴∠AFE=∠CEF=68°,
由折叠的性质可得,
∠CEF=∠C′EF,
∴∠C′EF=68°,
故选:A.
11.解:过F点作FG∥AB,
∵AB∥CD,
∴FG∥CD,
∴∠BFG=∠ABF,∠DFG+∠CDF=180°,
∵BF⊥DE,
∴∠BFD=90°,
∵BF平分∠ABE,
∴∠ABE=2∠ABF,
∴∠BFG+∠DFG+∠CDF=∠ABF+180°,
∴90°+∠CDE=∠ABE+180°,即∠EDC﹣∠ABE=90°.
故选:C.
12.解:如图,延长AE交CD于点F,
∵AB∥CD,
∴∠BAE+∠EFC=180°,
又∵∠BAE=120°,
∴∠EFC=180°﹣∠BAE=180°﹣120°=60°,
又∵∠DCE=30°,
∴∠AEC=∠DCE+∠EFC=30°+60°=90°.
故选:C.
13.解:设∠BCE=∠ECF=∠BCF=x,
∵∠DAC=3∠BCF,
∴∠DAC=6x,
∵∠DAC+∠ACB=180°,
∴6x+x+x+20°=180°,
解得x=20°,
所以,∠FEC的度数为20°.
故选:B.
14.解:过∠2的顶点,作如图所示的射线l,使l∥l1,
∵l1∥l2,l∥l1,
∴l1∥l2∥l.
∴∠1=∠α,∠2=∠β.
∵∠α+∠β=∠2,
∴∠1+∠3=∠2.
故选:D.
15.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
16.解:∵∠2=30°,∠CAB=90°,
∴∠1=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE,故①正确;
∵∠CAB=∠DAE=90°,
∴∠BAE+∠CAD=90°﹣∠1+90°+∠1=180°,故②正确;
∵BC∥AD,∠B=45°,
∴∠3=∠B=45°,
∵∠2+∠3=∠DAE=90°,
∴∠2=45°,故③错误;
∵∠CAD=150°,∠BAE+∠CAD=180°,
∴∠BAE=30°,
∵∠E=60°,
∴∠BOE=∠BAE+∠E=90°,
∴∠4+∠B=90°,
∵∠B=45°,
∴∠4=45°,
∵∠C=45°,
∴∠4=∠C,故④正确;
所以其中正确的结论有①②④,3个.
故选:C.
17.解:过G作直线MN∥AB,如下图所示,
∵MN∥AB,
∴∠2=∠3(两直线平行,内错角相等),
∵MN∥AB,AB∥CD,
∴MN∥CD,
∴∠5=∠4(两直线平行,内错角相等),
∴∠EGF=∠3+∠5=∠2+∠4=60°,
∵∠EFG=90°,
∴∠1+∠4=180°﹣90°=90°,
∴∠2=60°﹣∠4=60°﹣(90°﹣∠1)=∠1﹣30°=55°﹣30°=25°,
故选:C.
18.解:如右图所示,
∵CD∥AB,
∴∠4=∠3,
∵∠4=∠2+(180°﹣∠1),
∴∠3=∠2+(180°﹣∠1),
∴∠1﹣∠2=180°﹣∠3,
故选:B.
19.解:过P作直线MN∥AB,如下图所示,
∵MN∥AB,
∴∠A+∠1=180°(两直线平行,同旁内角互补),
∴∠1=180°﹣∠A=180°﹣120°=60°,
∵MN∥AB,AB∥CD,
∴MN∥CD,
∴∠C+∠2=180°(两直线平行,同旁内角互补),
∴∠2=180°﹣∠C=180°﹣130°=50°,
∴∠APC=∠1+∠2=60°+50°=110°,
故选:B.
20.解:如下图所示,
①∵AB∥CD,
∴∠DFE=∠AEF(两直线平行,内错角相等),
故①正确;
②∵EM平分∠BEF,
∴∠3=∠4,
∵FM平分∠EFD,
∴∠5=∠6,
∵AB∥CD,
∴∠3+∠4+∠5+∠6=180°(两直线平行,同旁内角互补),
∴∠3+∠5=90°,
∴∠EMF=180°﹣∠3﹣∠5=180°﹣90°=90°,
故②正确;
③∵AB∥CD,
∴∠1+∠2=∠5+∠6(两直线平行,内错角相等),
∵EG平分∠AEF,
∵∠1=∠2,
∵FM平分∠EFD,
∴∠5=∠6,
∴∠1=∠6,
∴∠DFM=∠AEG,
故③正确;
④由题意得∠AEF=∠1+∠2,∠EGC=∠2+∠EFG,
∵根据题意无法判断∠1与∠EFG的大小关系,
∴∠AEF不一定等于∠EFG,
故④不正确;
综上所述,正确的结论有3个,
故选:C.
21.解:设AE与CD相交于M点,如下图所示,
A.∵AB∥CD,
∴∠A=∠AMC(两直线平行,内错角相等),
∵∠AMC=∠C+∠E(外角的性质),
∴∠AMC>∠C,
∴∠A>∠C,
故A选项不符合题意;
B.由题意得无法根据AB∥CD得出∠C与∠E的关系,故B选项不符合题意;
C.∵AB∥CD,
∴∠A=∠AMC(两直线平行,内错角相等),
∵∠AMC=∠C+∠E(外角的性质),
∴∠A=∠C+∠E,
故C选项符合题意;
D.∵AB∥CD,
∴∠A=∠AMC(两直线平行,内错角相等),
∵∠AMC=∠C+∠E(外角的性质),
∴∠AMC>∠C,
∴∠A>∠C,
∴∠C<∠A+∠E
∴故D选项不符合题意;
故选:C.
22.解:∵AE∥BD,∠2=40°,
∴∠CEA=∠2=40°,
又∵∠1=115°,
∴∠C=180°﹣∠CEA﹣∠1=180°﹣115°﹣40°=25°.
故选:B.
23.解:∵AC=AB,
∴∠ACB=∠ABC=55°,
根据三角形的内角和定理得:∠ACB+∠ABC+∠CAB=180°,
∴∠CAB=180°﹣∠ACB﹣∠ABC=180°﹣55°﹣55°=70°,
∵l1∥l2,
∴∠1=∠CAB=70°,
故答案为:70°.
24.解:∵AB∥CD,
∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,
∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠1+∠3=45°,
∵∠5=∠2+∠3,
∴∠5=∠1+∠3=45°,
即∠BFD=45°,
故答案为:45°.
25.解:∵AB∥CD,
∴∠FGB+∠GFD=180°,
∴∠GFD=180°﹣∠FGB=26°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=52°,
∵AB∥CD,
∴∠AEF=∠EFD=52°.
故答案为:52°.
26.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
27.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°﹣∠A=180°﹣60°=120°.
(2)∵BC平分∠ABP,BD平分∠PBN,
∴∠CBP=∠ABP,∠PBD=∠PBN,
∴∠CBD=∠CBP+∠PBD=∠ABP+∠PBN=∠ABN=60°.
(3)不变,∠APB=2∠ADB,理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PDN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB.
28.(1)证明:∵AC∥BD,
∴∠DAE=∠BDA,
∵∠BDA=∠C,
∴∠DAE=∠C,
∴AD∥BC;
(2)证明:如图2,设CE与BD相交于点G,∠BGA=∠BDA+DAE,
∵BD⊥BC,
∴∠BGA+∠C=90°,
∴∠BDA+∠DAE+∠C=90°,
∵∠BDA=∠C,
∴∠DAE+2∠C=90°;
(3)如图3,设∠DAE=α,则∠DFE=8α,
∵∠DFE+∠AFD=180°,
∴∠AFD=180°﹣8α,
∵DF∥BC,
∴∠C=∠AFD=180°﹣8α,
又∵2∠C+∠DAE=90°,
∴2(180°﹣8α)+α=90°,
∴α=18°,
∴∠C=180°﹣8α=36°=∠ADB,
又∵∠C=∠BDA,∠BAC=∠BAD,
∴∠ABC=∠ABD=∠CBD=45°,
△ABD中,∠BAD=180°﹣45°﹣36°=99°.
答:∠BAD的度数是99°.
29.证明:∵DE∥AB(已知),
∴∠A=∠CED(两直线平行,同位角相等)
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD(等量代换)
∴DF∥AE(同位角相等,两直线平行)
∴∠EGF+∠AEG=180°(两直线平行,同旁内角互补)
故答案为:两直线平行,同位角相等;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补.
30.证明:连接EF
∵FG⊥AC,HE⊥AC,
∴∠FGC=∠HEC=90°(垂线的性质).
∴FG∥HE(同位角相等,两直线平行).
∴∠3=∠4(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4.
即∠DEF=∠EFC
∴DE∥BC(内错角相等,两直线平行).
故答案为:垂线的性质;FG,HE,同位角相等,两直线平行;4,两直线平行,内错角相等;内错角相等,两直线平行.
31.证明:∵∠A=112°,∠ABC=68°(已知),
∴∠A+∠ABC=180°.
∴AD∥BC(同旁内角互补,两直线平行).
∴∠1=∠3
(两直线平行,内错角相等
).
∵BD⊥DC,EF⊥DC(已知),
∴∠BDF=90°,∠EFC=90°(垂直的定义).
∴∠BDF=∠EFC=90°.
∴BD∥EF(同位角相等,两直线平行).
∴∠2=∠3(两直线平行,同位角相等).
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;∠3;两直线平行,内错角相等;垂直的定义;
同位角相等,两直线平行;∠3;两直线平行,同位角相等;等量代换.
32.解:(1)如图1,过P作PM∥AB,
∴∠APM+∠PAB=180°,
∴∠APM=180°﹣125°=55°,
∵AB∥CD,
∴PM∥CD,
∴∠CPM+∠PCD=180°,
∴∠CPM=180°﹣115°=65°,
∴∠APC=55°+65°=120°;
故答案为:120;
(2)如图2,∠APC=∠α+∠β,理由如下:
过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图3,当P在BD延长线时,∠APC=∠α﹣∠β;理由:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE﹣∠CPE=∠α﹣∠β;
如图4,当P在DB延长线时,∠APC=∠β﹣∠α;理由:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠CPE﹣∠APE=∠β﹣∠α;
33.解:①∵AB∥CD,∠α=50°
∴∠2=∠α=50°,
故答案为50;
(2)∠α=∠1+∠2.
证明:过P作PG∥AB,
∵AB∥CD,
∴PG∥AB∥CD,
∴∠2=∠EPG,∠1=∠FPG,
∵∠α=∠EPF=∠EPG+∠FPG,
∴∠α=∠1+∠2;
(3)不成立.
理由:过P作PH∥AB,
∵AB∥CD,
∴PH∥AB∥CD,
∴∠2=∠EPH,∠1=∠FPH,
∵∠α=∠EPF=∠EPH﹣∠FPH,
∴∠α=∠2﹣∠1,
故不成立.
34.解:(1)∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=120°,∠PCD=130°,
∴∠APE=60°,∠CPE=50°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)①当点P在A、B两点之间,如图3,作PQ∥AD,
∵PQ∥AD,AD∥BC,
∴PQ∥AD∥BC,
∴∠DPQ=∠β,∠CPQ=∠γ,
∵∠CPD=∠DPQ+∠CPQ,
∴∠α=∠β+∠γ;
②当点P在B、O两点之间时,作PQ∥AD,
∵PQ∥AD,AD∥BC,
∴PQ∥AD∥BC,
∴∠DPQ=∠β,∠CPQ=∠γ,
∵∠CPD=∠DPQ﹣∠CPQ,
∴∠α=∠β﹣∠γ
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
