2020-2021学年苏科版七年级数学下册7.2探索平行线的性质 平行线的性质自主学习同步训练3(Word版 附答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册7.2探索平行线的性质 平行线的性质自主学习同步训练3(Word版 附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 678.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 00:00:00 | ||
图片预览

文档简介
2021年苏科新版七年级数学下册7.2平行线的性质自主学习同步训练3(附答案)
1.如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H.点F是边AB上一点.使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G,若∠DEH=100°,则∠BEG的度数为( )
A.30°
B.40°
C.50°
D.60°
2.已知直线AB∥CD,点P、Q分别在AB、CD上,如图所示,射线PB按顺时针方向以每秒4°的速度旋转至PA便立即回转,并不断往返旋转;射线QC按顺时针方向每秒1°旋转至QD停止,此时射线PB也停止旋转.
(1)若射线PB、QC同时开始旋转,当旋转时间30秒时,PB'与QC'的位置关系为
;
(2)若射线QC先转45秒,射线PB才开始转动,当射线PB旋转的时间为
秒时,PB′∥QC′.
3.如图,直线AB∥CD,直线EF与AB,CD分别交于点E,F,∠AEF与∠CFE的角平分线交于点P,延长FP交AB于点G,过点G作GQ⊥FG交直线EF于点Q,连接PQ,点M是QG延长线上的一点,且∠PQM=∠QPM,若PN平分∠FPM交CD于点N,则∠NPQ的度数为
.
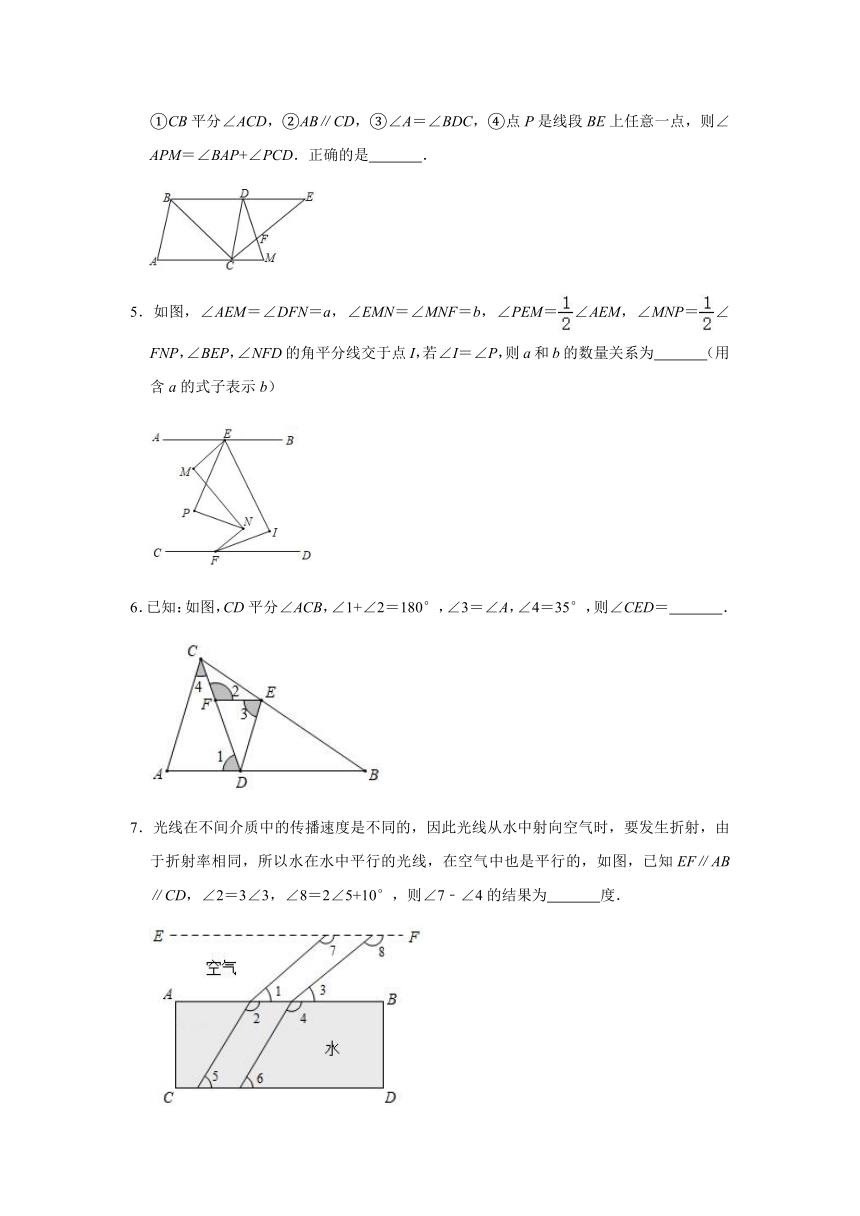
4.如图,已知AC∥BD,BC平分∠ABD,CE平分∠DCM,且BC⊥CE.则下列结论:①CB平分∠ACD,②AB∥CD,③∠A=∠BDC,④点P是线段BE上任意一点,则∠APM=∠BAP+∠PCD.正确的是
.
5.如图,∠AEM=∠DFN=a,∠EMN=∠MNF=b,∠PEM=∠AEM,∠MNP=∠FNP,∠BEP,∠NFD的角平分线交于点I,若∠I=∠P,则a和b的数量关系为
(用含a的式子表示b)
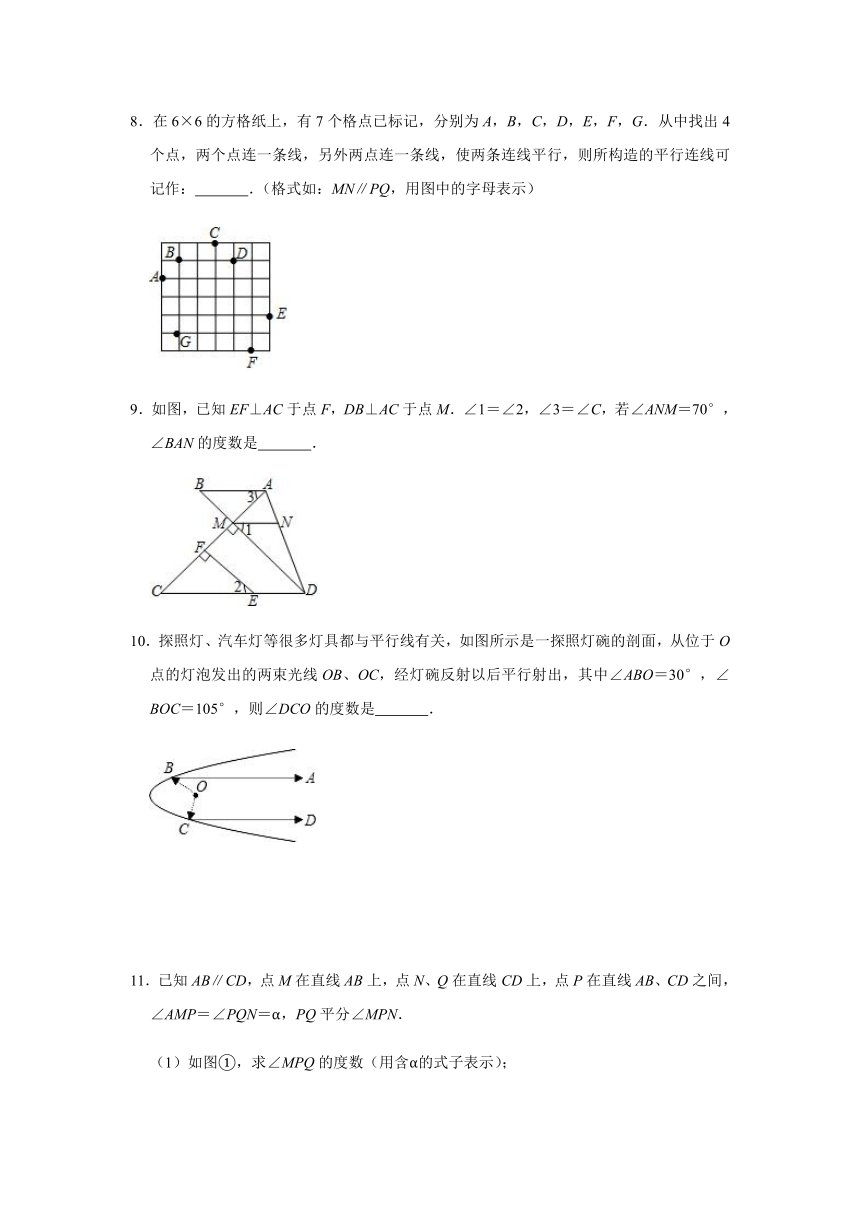
6.已知:如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=
.
7.光线在不间介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射,由于折射率相同,所以水在水中平行的光线,在空气中也是平行的,如图,已知EF∥AB∥CD,∠2=3∠3,∠8=2∠5+10°,则∠7﹣∠4的结果为
度.
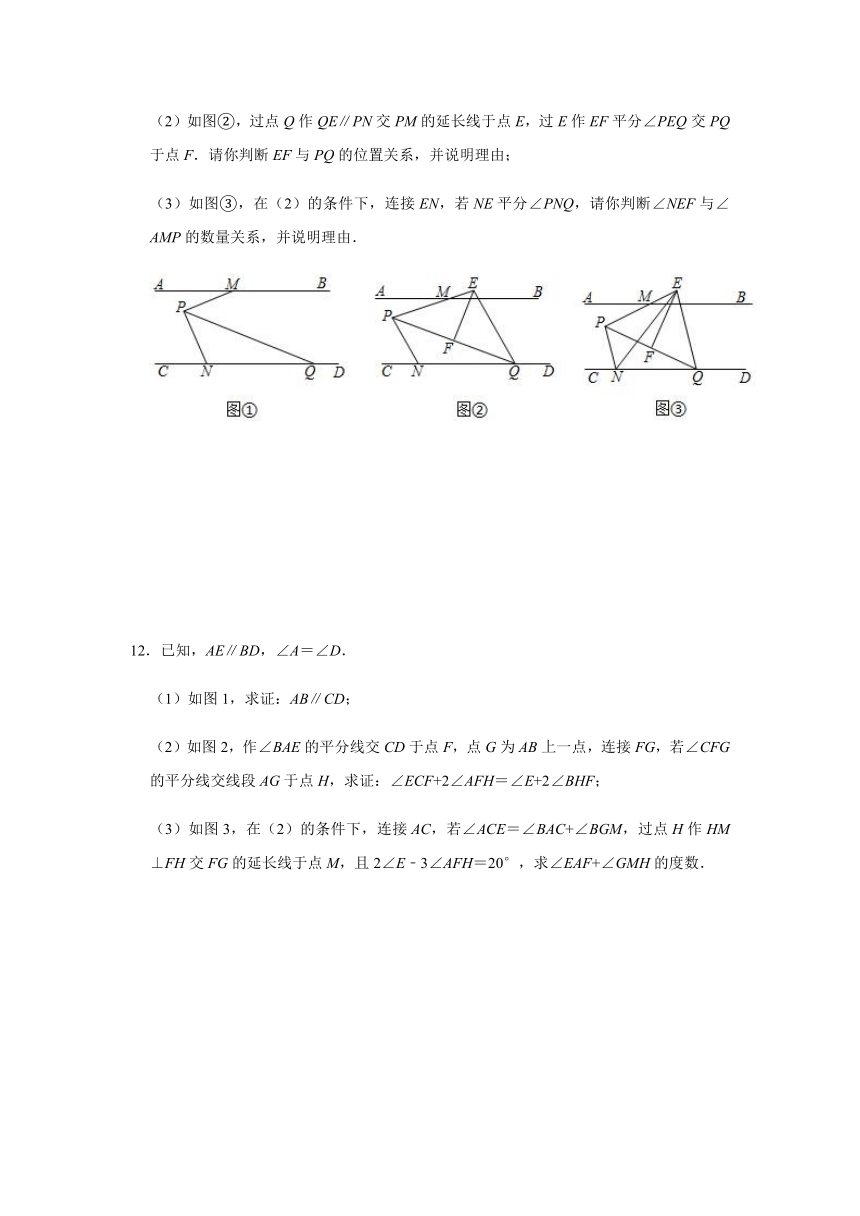
8.在6×6的方格纸上,有7个格点已标记,分别为A,B,C,D,E,F,G.从中找出4个点,两个点连一条线,另外两点连一条线,使两条连线平行,则所构造的平行连线可记作:
.(格式如:MN∥PQ,用图中的字母表示)
9.如图,已知EF⊥AC于点F,DB⊥AC于点M.∠1=∠2,∠3=∠C,若∠ANM=70°,∠BAN的度数是
.
10.探照灯、汽车灯等很多灯具都与平行线有关,如图所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB、OC,经灯碗反射以后平行射出,其中∠ABO=30°,∠BOC=105°,则∠DCO的度数是
.
11.已知AB∥CD,点M在直线AB上,点N、Q在直线CD上,点P在直线AB、CD之间,∠AMP=∠PQN=α,PQ平分∠MPN.
(1)如图①,求∠MPQ的度数(用含α的式子表示);
(2)如图②,过点Q作QE∥PN交PM的延长线于点E,过E作EF平分∠PEQ交PQ于点F.请你判断EF与PQ的位置关系,并说明理由;
(3)如图③,在(2)的条件下,连接EN,若NE平分∠PNQ,请你判断∠NEF与∠AMP的数量关系,并说明理由.
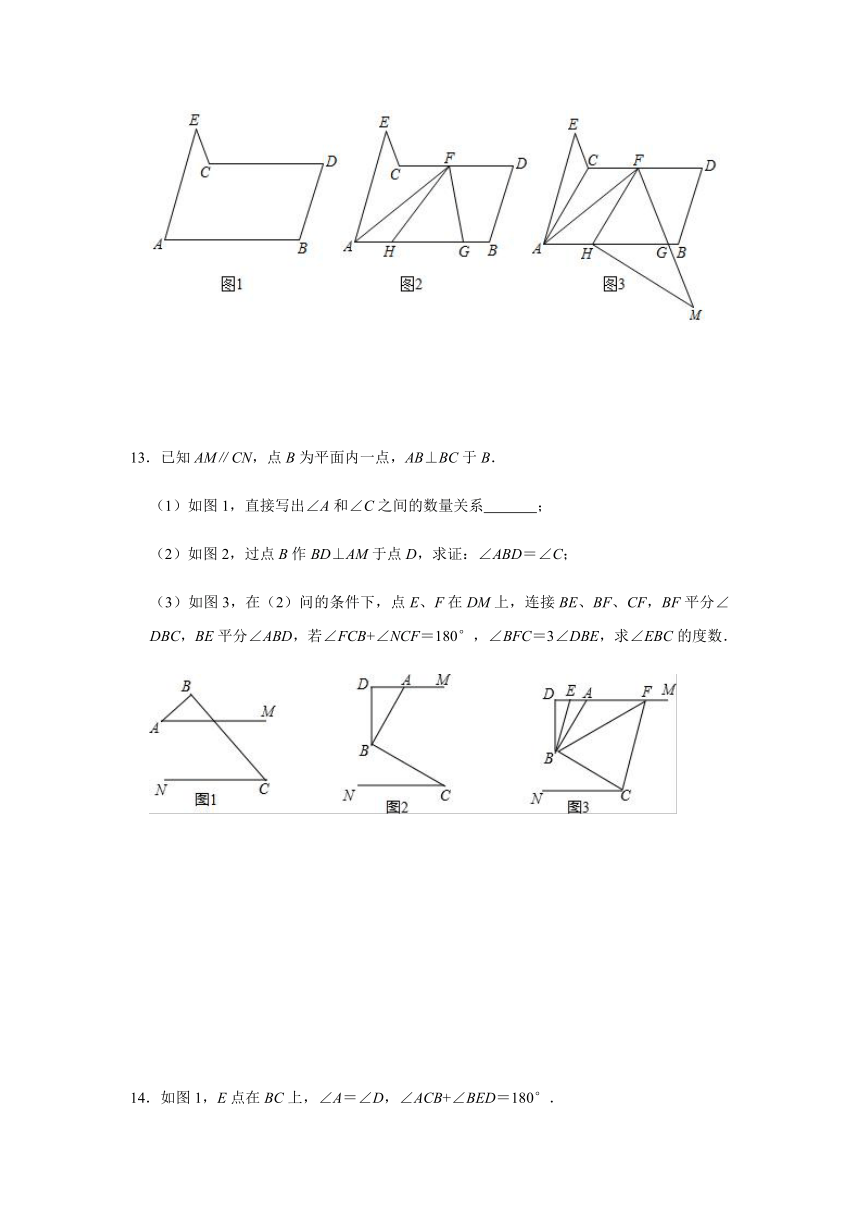
12.已知,AE∥BD,∠A=∠D.
(1)如图1,求证:AB∥CD;
(2)如图2,作∠BAE的平分线交CD于点F,点G为AB上一点,连接FG,若∠CFG的平分线交线段AG于点H,求证:∠ECF+2∠AFH=∠E+2∠BHF;
(3)如图3,在(2)的条件下,连接AC,若∠ACE=∠BAC+∠BGM,过点H作HM⊥FH交FG的延长线于点M,且2∠E﹣3∠AFH=20°,求∠EAF+∠GMH的度数.
13.已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系
;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
14.如图1,E点在BC上,∠A=∠D,∠ACB+∠BED=180°.
(1)求证:AB∥CD;
(2)如图2,AB∥CD,BG平分∠ABE,与∠EDF的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.
(3)保特(2)中所求的∠DEB的度数不变,如图3,BM平分∠EBK,DN平分∠CDE,作BP∥DN,则∠PBM的度数是否改变?若不变,请求值;若改变,请说明理由.
15.如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.
(1)判断DE与BF是否平行?并说明理由;
(2)试说明:∠C=2∠P.
16.完成下面的解题过程:
如图,AD∥BC,点F是AD上一点,CF与BA的延长线相交于点E,且∠1=∠2,∠3=∠4.CD与BE平行吗?为什么?
解:CD∥BE,理由如下:
∵AD∥BC(已知),
∴∠4=
(
)
∵∠3=∠4(已知),
∴∠3=
(
)
∵∠1=∠2(已知),
∴∠1+∠ACE=∠2+∠ACE
(
)
即∠BCE=
∴∠3=
∴CD∥BE(
)
17.如图,取一副三角板按图1拼接,固定三角板ADE(含30°),将三角板ABC(含45°)绕点A顺时针方向旋转一个大小为α的角(0°<α≤45°),试问:
(1)当∠α=
度时,能使图2中的AB∥DE;
(2)当旋转到AB与AE重叠时(如图3),则∠α=
度;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;
(4)当0°<α≤45°时,连接BD(如图4),探求∠DBC+∠CAE+∠BDE的值的大小变化情况,并说明理由.
18.如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
(1)求证:EM∥NG;
(2)连接EG,在GN上取一点H,使∠HEG=∠HGE,作∠FEH的平分线EP交AB于点P,求∠PEG的度数.
19.如图1,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠DCE﹣∠HAE=90°.(1)求证:BH∥CD.
(2)如图2:直线AF交DC于F,AM平分∠EAF,AN平分∠BAE.试探究∠MAN,∠AFG的数量关系.
20.如图,已知直线AB∥CD,直线EF分别与AB、CD相交于点E、F,FM平分∠EFD,点H是射线EA上一动点(不与点E重合),过点H的直线交EF于点P,HM平分∠BHP交FM于点M.
(1)如图1,试说明:∠HMF=(∠BHP+∠DFP);
请在下列解答中,填写相应的理由:
解:过点M作MQ∥AB(过直线外一点有且只有一条直线与这条直线平行).
∵AB∥CD(已知),
∴MQ∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠1=∠3,∠2=∠4(
)
∴∠1+∠2=∠3+∠4(等式的性质)
即∠HMF=∠1+∠2.
∵FM平分∠EFD,HM平分∠BHP(已知)
∵∠1=∠BHP,∠2=∠DFP(
)
∴∠HMF=∠BHP+∠DFP=(∠BHP+∠DFP)(等量代换).
(2)如图2,若HP⊥EF,求∠HMF的度数;
(3)如图3,当点P与点F重合时,FN平分∠HFE交AB于点N,过点N作NQ⊥FM于点Q,试说明无论点H在何处都有∠EHF=2∠FNQ.
21.如图1,已知AB∥CD,∠B=30°,∠D=120°;
(1)若∠E=60°,则∠F=
;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
22.已知,AB∥CD,CF平分∠ECD.
(1)如图1,若∠DCF=25°,∠E=20°,求∠ABE的度数.
(2)如图2,若∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,求∠ABE的度数.
(3)如图3,在(2)的条件下,P为射线BE上一点,H为CD上一点,PK平分∠BPH,HN∥PK,HM平分∠DHP,∠DHQ=2∠DHN,求∠PHQ的度数.
23.已知,AB∥CD,点E为射线FG上一点.
(1)如图1,若∠EAF=30°,∠EDG=40°,则∠AED=
°;
(2)如图2,当点E在FG延长线上时,此时CD与AE交于点H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图3,DI平分∠EDC,交AE于点K,交AI于点I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD的度数.
24.如图1,AB∥CD,直线EF交AB于点E,交CD于点F,点G在CD上,点P在直线EF左侧、且在直线AB和CD之间,连接PE、PG.
(1)求证:∠EPG=∠AEP+∠PGC;
(2)连接EG,若EG平分∠PEF,∠AEP+∠PGE=110°,∠PGC=∠EFC,求∠AEP的度数;
(3)如图2,若EF平分∠PEB,∠PGC的平分线所在的直线与EF相交于点H,则∠EPG与∠EHG之间的数量关系为
.
25.已知E、D分别在∠AOB的边OA、OB上,C为平面内一点,DE、DF分别是∠CDO、∠CDB的平分线.
(1)如图1,若点C在OA上,且FD∥AO,求证:DE⊥AO;
(2)如图2,若点C在∠AOB的内部,且∠DEO=∠DEC,请猜想∠DCE、∠AEC、∠CDB之间的数量关系,并证明;
(3)若点C在∠AOB的外部,且∠DEO=∠DEC,请根据图3、图4分别写出∠DCE、∠AEC、∠CDB之间的数量关系(不需证明).
26.已知:射线OP∥AE
(1)如图1,∠AOP的角平分线交射线AE与点B,若∠BOP=58°,求∠A的度数.
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ADO=39°,求∠ABO﹣∠AOB的度数.
(3)如图3,若∠A=m,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,∠Bn﹣1OP的角平分线OBn,其中点B,B1,B2,…,Bn﹣1,Bn都在射线AE上,试求∠ABnO的度数.
27.(1)如图1,已知直线AB∥CD,点E是AB上方一点,MF平分∠AME,若点G恰好在MF的反向延长线上,且NE平分∠CNG,2∠E与∠G互余,求∠AME的大小.
(2)如图2,在(1)的条件下,若点P是EM上一动点,PQ平分∠MPN,NH平分∠PNC,交AB于点H,PJ∥NH,当点P在线段EM上运动时,∠JPQ的度数是否改变?若不变,求出其值;若改变,请说明你的理由.
28.如图,在△ABC中,∠B=∠C,∠BAC=80°,AD∥EF,∠1=∠2,求∠BDG的度数.
29.如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=50°,∠F=25°.
(1)求证:EG⊥BD;
(2)求∠CDB的度数.
30.如图,已知射线CD∥AB,∠C=∠ABD=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.
(1)求∠FAD的度数;
(2)若向右平行移动BD,其它条件不变,那么∠ADC:∠AEC的值是否发生变化?若变化,找出其中规律;若不变,求出这个比值;
(3)在向右平行移动BD的过程中,是否存在某种情况,使∠AFC=∠ADB?若存在,请求出∠ADB度数;若不存在,说明理由.
31.请将下列题目的证明过程补充完整:
如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2,求证:DE∥BC.
证明:连接EF.
∵FG⊥AC,HE⊥AC,
∴∠FGC=∠HEC=90°.
∴FG∥
(
).
∴∠3=∠
(
).
又∵∠1=∠2,
∴
=∠2+∠4,
即∠
=∠EFC.
∴DE∥BC(
).
32.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
33.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图1,求证:CF∥AB;
(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(3)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.
34.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
35.如图:已知:∠ADE+∠BCF=180°,BE平分∠ABC交CD的延长线于点E,AF平分∠BAD交DC的延长线于点F,若∠ABC=2∠E,则∠E+∠F=90°,完成下列推理过程.
证明:
∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°
∴∠ADF=∠BCF(
)
∴AD∥BC(
)
∵BE平分∠ABC
∴∠ABC=2∠ABE(
)
又∵∠ABC=2∠E
∴∠ABE=∠E
∴AB∥EF(
)
∵AD∥BC
∴∠BAD+∠ABC=180°(
)
∵BE平分∠ABC,AF平分∠BAD
∴∠ABE=∠ABC,∠BAF=∠BAD
∴∠ABE+∠BAF=∠ABC+∠BAD=×180°=90°
∵AB∥EF(
)
∴∠BAF=∠F(
)
∵∠ABE=∠E
∴∠E+∠F=90°(
)
36.如图,点D为线段BC上的一点,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,那么AD平分∠BAC吗?请说明理由.
37.如图,AF的延长线与BC的延长线交于点E,AD∥BE,∠1=∠2=30°,∠3=∠4=80°.
(1)求∠CAE的度数;
(2)求证:AB∥DC.
38.如图,AD交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)证明AD∥EF;
(2)若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,则∠BAD和∠CAD相等吗?请说明理由;
(3)在(2)的条件下,若FH⊥BC,∠C=30°,求∠F的度数.
39.如图,已知∠A+∠3=180°,∠1=∠2,∠D=80°,∠CBD=70°.
(1)试说明AB∥CD;
(2)求∠CBA的度数.
40.如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.
(1)求证:AB∥CD;
(2)若BC平分∠ABD,∠D=112°,求∠C的度数.
参考答案
1.解:设FBE=∠FEB=α,则∠AFE=2α,
∠FEH的角平分线为EG,设∠GEH=∠GEF=β,
∵AD∥BC,∴∠ABC+∠BAD=180°,
而∠D=∠ABC,∴∠D+∠BAD=180°,∴AB∥CD,
∠DEH=100°,则∠CEH=∠FAE=80°,
∠AEF=180°﹣∠FEG﹣∠HEG=180°﹣2β,
在△AEF中,
在△AEF中,80°+2α+180﹣2β=180°
故β﹣α=40°,
而∠BEG=∠FEG﹣∠FEB=β﹣α=40°,
故选:B.
2.解:(1)如图1,当旋转时间30秒时,由已知得∠BPB′=4°×30=120°,∠CQC′=30°,
过E作EF∥AB,则EF∥CD,
∴∠PEF=180°﹣∠BPB′=60°,∠QEF=∠CQC′=30°,
∴∠PEQ=90°,
∴PB′⊥QC′,
故答案为:PB′⊥QC′;
(2)①当0s<t≤45时,如图2,则∠BPB′=4t°,∠CQC′=45°+t°,
∵AB∥CD,PB′∥QC′,
∴∠BPB′=∠PEC=∠CQC′,
即4t=45+t,
解得,t=15(s);
②当45s<t≤67.5s时,如图3,则∠APB′=4t﹣180°,∠CQC'=t+45°,
∵AB∥CD,PB′∥QC′,
∴∠APB′=∠PED=180°﹣∠CQC′,
即4t﹣180=180﹣(45+t),
解得,t=63(s);
③当67.5s<t<135s时,如图4,则∠BPB′=4t﹣360°,∠CQC′=t+45°,
∵AB∥CD,PB′∥QC′,
∴∠BPB′=∠PEC=∠CQC′,
即4t﹣360=t+45,
解得,t=135(s);
综上,当射线PB旋转的时间为15秒或63秒或135秒时,PB′∥QC′.
故答案为:15秒或63秒或135秒.
3.解:设∠PQM=∠QPM=x°,
∵PN平分∠MPF,
∴∠MPN=∠FPN,
设∠MPN=∠FPN=y°,
∵∠AEF与∠CFE的角平分线交于点P,
∴∠PEF=,∠EFP=,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴∠PEF+∠PFE==90°,
∴∠EPF=180°﹣(∠PEF+∠PFE)=180°﹣90°=90°,
∵GQ⊥PF,
∴∠QGP=90°,
∴∠QGP=∠EPF,
∴GQ∥EP,
∴∠PQM=∠QPE=x°,
∵∠QPE+∠QPM+∠FPN+∠NPM+∠EPF=360°,
∴x+x+y+y+90=360,
∴x+y=135,
即∠QPM+∠NPM=135°,
∴∠NPQ=∠QPM+∠NPM=135°.
4.解:如图,
∵AC∥BD,
∵∠2=∠3
∵BC平分∠ABD,
∴∠1=∠2,
∴∠1=∠3,
∵CE平分∠DCM,
∴∠4=∠5,
∵BC⊥CE.
∴∠4+∠6=90°,
∴∠5+∠6=90°,
∵∠3+∠5=90°,
∴∠3=∠6,
∴CB平分∠ACD,故①正确;
∴∠1=∠6,
AB∥CD,故②正确;
∴四边形ABCD是平行四边形,
∴∠A=∠BDC,故③正确;
如图,点P是线段BE上任意一点,
∵AB与PC不平行,CD与PM不平行,
∴∠BAP≠∠APC,∠PCD≠∠CPM,
∴∠APM≠∠BAP+∠PCD.故④不正确.
所以正确的是①②③.
故答案为:①②③.
5.解:分别过点P、I作ME∥PH,AB∥GI,
设∠AEM=2x,∠PNF=2y,则∠PEM=x,∠MNP=y,
∴∠DFN=2x,
∵PH∥ME,
∴∠EPH=x,
∵EM∥FN,
∴PH∥FN,
∴∠HPN=2y,∠EPN=x+2y,
同理,∠EIF=,
∵∠EPN=∠EIF,
∴=x+2y,
∴,
∴,
故答案为:.
6.解:∵∠1+∠2=180°,∠1+∠BDC=180°
∴∠2=∠BDC
∴EF∥AB
∴∠3=∠BDE
∵∠3=∠A
∴∠A=∠BDE
∴AC∥DE
∴∠ACB+∠CED=180°
∵CD平分∠ACB,∠4=35°
∴∠ACB=2∠4=2×35°=70°
∴∠CED=180°﹣∠ACB=180°﹣70°=110°
故答案为:110°.
7.解:∵EF∥AB∥CD,
∴∠4=∠2,∠5=∠6,∠7=∠8,∠4+∠6=180°,∠3+∠8=180°,
∴∠4=180°﹣∠6,∠3=180°﹣∠8=180°﹣∠7,
∵∠2=3∠3,∠8=2∠5+10°,
∴∠4=3∠3,∠7=2∠5+10°=2(180°﹣∠4)+10°=2(180°﹣3∠3)+10°=2[180°﹣3(180°﹣∠7)]+10°,
∴∠7=142°,
∴∠4=3∠3=3(180°﹣∠7)=114°,
∴∠7﹣∠4=28°,
故答案为:28.
8.解:如图所示,过A、G两点作直线AG,过C、F两点作直线CF,
根据方格的性质得出:∠1=∠2,
∵tan∠1==3,tan∠3==3,
∴∠1=∠3,
∴∠2=∠3,
∴AG∥CF,
故答案为:AG∥CF.
9.解:∵EF⊥AC,DB⊥AC,
∴∠EFC=∠DMC=90°,
∴BD∥FE,
∴∠2=∠BDC,
∵∠1=∠2,
∴∠1=∠BDC,
∴MN∥CD,
∵∠3=∠C,
∴AB∥CD,
∴MN∥AB,
∴∠BAN+∠ANM=180°,
∵∠ANM=70°,
∴∠BAN=110°,
故答案为:110°.
10.解:过O点作OH∥AB,则∠ABO=∠HOB=30°,
∵∠BOC=105°,
∴∠HOC=105°﹣30°=75°,
∵AB∥CD,
∴OH∥CD,
∴∠HOC=∠DCO=75°.
故答案为:75°.
11.解:(1)如图①,过点P作PR∥AB,
∵AB∥CD,
∴AB∥CD∥PR,
∴∠AMP=∠MPR=α,∠PQN=∠RPQ=α,
∴∠MPQ=∠MPR+∠RPQ=2α;
(2)如图②,EF⊥PQ,理由如下:
∵PQ平分∠MPN.
∴∠MPQ=∠NPQ=2α,
∵QE∥PN,
∴∠EQP=∠NPQ=2α,
∴∠EPQ=∠EQP=2α,
∵EF平分∠PEQ,
∴∠PEQ=2∠PEF=2∠QEF,
∵∠EPQ+∠EQP+∠PEQ=180°,
∴2∠EPQ+2∠PEF=180°,
∴∠EPQ+∠PEF=90°,
∴∠PFE=180°﹣90°=90°,
∴EF⊥PQ;
(3)如图③,∠NEF=∠AMP,理由如下:
由(2)可知:∠EQP=2α,∠EFQ=90°,
∴∠QEF=90°﹣2α,
∵∠PQN=α,
∴∠NQE=∠PQN+∠EQP=3α,
∵NE平分∠PNQ,
∴∠PNE=∠QNE,
∵QE∥PN,
∴∠QEN=∠PNE,
∴∠QNE=∠QEN,
∵∠NQE=3α,
∴∠QNE=(180°﹣∠NQE)=(180°﹣3α),
∴∠NEF=180°﹣∠QEF﹣∠NQE﹣∠QNE
=180°﹣(90°﹣2α)﹣3α﹣(180°﹣3α)
=180°﹣90°+2α﹣3α﹣90°+α
=α
=∠AMP.
∴∠NEF=∠∠AMP.
12.(1)证明:∵AE∥BD,
∴∠A+∠B=180°,
∵∠A=∠D,
∴∠D+∠B=180°,
∴AB∥CD;
(2)证明:如图2,过点E作EP∥CD,
∵AB∥CD,
∴AB∥EP,
∴∠PEA=∠EAB,∠PEC=∠ECF,
∵∠AEC=∠PEC﹣∠PEA,
∴∠AEC=∠ECF﹣∠EAB,
即∠ECF=∠AEC+∠EAB,
∵AF是∠BAE的平分线,
∴∠EAF=∠FAB=EAB,
∵FH是∠CFG的平分线,
∴∠CFH=∠HFG=CFG,
∵CD∥AB,
∴∠BHF=∠CFH,∠CFA=∠FAB,
设∠FAB=α,∠CFH=β,
∵∠AFH=∠CFH﹣∠CFA=∠CFH﹣∠FAB,
∴∠AFH=β﹣α,∠BHF=∠CFH=β,
∴∠ECF+2∠AFH=∠AEC+∠EAB+2∠AFH=∠AEC+2α+2(β﹣α)=∠AEC+2β,
∴∠ECF+2∠AFH=∠E+2∠BHF;
(3)解:如图,延长DC至点Q,
∵AB∥CD,
∴∠QCA=∠CAB,∠BGM=∠DFG,∠CFH=∠BHF,∠CFA=∠FAG,
∵∠ACE=∠BAC+∠BGM,
∴∠ECQ+∠QCA=∠BAC+∠BGM,
∴∠ECQ=∠BGM=∠DFG,
∵∠ECQ+∠ECD=180°,∠DFG+∠CFG=180°,
∴∠ECF=∠CFG,
由(2)问知:∠ECF+2∠AFH=∠AEC+2∠BHF,∠CFG=2∠CFH=2∠BHF,
∴∠AEC=2∠AFH,
∵2∠AEC﹣3∠AFH=20°,
∴∠AFH=20°,
由(2)问知:∠CFM=2β,∠FHG=β,
∵FH⊥HM,
∴∠FHM=90°,
∴∠GHM=90°﹣β,
过点M作MN∥AB,
∴MN∥CD,
∴∠CFM+∠NMF=180°,∠GHM=∠HMN=90°﹣β,
∴∠HMB=∠HMN=90°﹣β,
由(2)问知:∠EAF=∠FAB,
∴∠EAF=∠CFA=∠CFH﹣∠AFH=β﹣20°,
∴∠EAF+∠GMH=β﹣20°+90°﹣β=70°,
∴∠EAF+∠GMH=70°.
13.解:(1)如图1,AM与BC的交点记作点O,
∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°,
故答案为:∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,BG∥AM,
∴CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
14.(1)证明:如图1,延长DE交AB于点F,
∵∠ACB+∠BED=180°,∠CED+∠BED=180°,
∴∠ACB=∠CED,
∴AC∥DF,
∴∠A=∠DFB,
∵∠A=∠D,
∴∠DFB=∠D,
∴AB∥CD;
(2)如图2,作EM∥CD,HN∥CD,
∵AB∥CD,
∴AB∥EM∥HN∥CD,
∴∠1+∠EDF=180°,∠MEB=∠ABE,
∵BG平分∠ABE,
∴∠ABG=ABE,
∵AB∥HN,
∴∠2=∠ABG,
∵CF∥HN,
∴∠2+∠β=∠3,
∴ABE+∠β=∠3,
∵DH平分∠EDF,
∴∠3=EDF,
∴ABE+∠β=EDF,
∴∠β=(∠EDF﹣∠ABE),
∴∠EDF﹣∠ABE=2∠β,
设∠DEB=∠α,
∵∠α=∠1+∠MEB=180°﹣∠EDF+∠ABE=180°﹣(∠EDF﹣∠ABE)=180°﹣2∠β,
∵∠DEB比∠DHB大60°,
∴∠α﹣60°=∠β,
∴∠α=180°﹣2(∠α﹣60°)
解得∠α=100°
∴∠DEB的度数为100°;
(3)∠PBM的度数不变,理由如下:
如图3,过点E作ES∥CD,设直线DF和直线BP相交于点G,
∵BM平分∠EBK,DN平分∠CDE,
∴∠EBM=∠MBK=EBK,
∠CDN=∠EDN=CDE,
∵ES∥CD,AB∥CD,
∴ES∥AB∥CD,
∴∠DES=∠CDE,
∠BES=∠ABE=180°﹣∠EBK,
∠G=∠PBK,
由(2)可知:∠DEB=100°,
∴∠CDE+180°﹣∠EBK=100°,
∴∠EBK﹣∠CDE=80°,
∵BP∥DN,
∴∠CDN=∠G,
∴∠PBK=∠G=∠CDN=CDE,
∴∠PBM=∠MBK﹣∠PBK
=∠EBK﹣CDE
=(∠EBK﹣∠CDE)
=80°
=40°.
15.解:(1)DE∥BF,
理由是:∵∠3=∠4,
∴BD∥CE,
∴∠5=∠FAB,
∵∠5=∠C,
∴∠C=∠FAB,
∴AB∥CD,
∴∠2=∠BGD,
∵∠1=∠2,
∴∠1=∠BGD,
∴DE∥BF;
(2)∵AB∥CD,
∴∠P=∠PDH,
∵DP平分∠BDH,
∴∠BDP=∠PDH,
∴∠BDP=∠PDH=∠P,
∵∠5=∠P+∠BDP,
∴∠5=2∠P,
∵∠C=∠5,
∴∠C=2∠P.
16.解:CD∥BE,理由如下:
∵AD∥BC(已知),
∴∠4=∠BCE(两直线平行,同位角相等)
∵∠3=∠4(已知),
∴∠3=∠BCE(等量代换)
∵∠1=∠2(已知),
∴∠1+∠ACE=∠2+∠ACE
(等式性质)
即∠BCE=∠ACD
∴∠3=∠ACD
∴CD∥BE(内错角相等,两直线平行)
故答案为:∠BCE;两直线平行,同位角相等;∠BCE;等量代换;等式性质;∠ACD;∠ACD;内错角相等,两直线平行.
17.解:(1)如图2,当AB∥DE时,∠BAE=∠E=30°,
∵∠BAC=45°,
∴∠CAE=45°﹣30°=15°,
即∠α=15°,
故答案为:15;
(2)当旋转到AB与AE重叠时,∠α=∠BAC=45°,
故答案为:45;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,旋转角α的所有可能的度数为15°,45°.
①当AB∥DE时,α=15°;
②当AD∥CB时,α=45°;
③当DE∥BC时,α=105°;
④当AE∥BC时,α=135°;
⑤当AC∥DE时,α=150°.
又∵0°<α≤45°,
∴旋转角α的所有可能的度数为15°,45°.
(4)如图4,当0°<α≤45°时,∠DBC+∠CAE+∠BDE=105°,保持不变;
理由:设BD分别交AE、AC于点M、N,
在△AMN中,∠AMN+∠CAE+∠ANM=180°,
∵∠ANM=∠C+∠DBC,∠AMN=∠E+∠BDE,
∴∠E+∠BDE+∠CAE+∠C+∠DBC=180°,
∵∠E=30°,∠C=45°,
∴∠DBC+∠CAE+∠BDE=180°﹣75°=105°.
18.解:(1)∵AB∥CD,
∴∠AMN+∠CNM=180°,
∵ME,NE分别是∠AMN与∠CNM的平分线,
∴∠EMN=∠AMN,∠ENM=∠MNC,
∴∠EMN+∠ENM=90°,即∠MEN=90°,
又∵NG⊥EN,
∴∠MEN+∠ENH=180°,
∴EM∥NG;
(2)设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°﹣2x,
∵EP平分∠FEH,
∴∠FEH=2∠PEH=2(∠PEG+x),
又∵∠FEH+∠HEN=180°,
∴2(∠PEG+x)+90°﹣2x=180°,
解得∠PEG=45°.
19.(1)证明:如图,延长AE交DC于F,
∵AE⊥CE,
∴∠CEF=90°,
根据三角形的外角性质,∠DCE﹣∠AFD=∠CEF=90°,
又∵∠DCE﹣∠HAE=90°,
∴∠HAE=∠AFD,
∴BH∥CD;
(2)解:∵AM平分∠EAF,AN平分∠BAE,
∴∠EAM=∠EAF,∠EAN=∠BAE=(∠EAF+∠BAF),
∴∠MAN=∠EAN﹣∠EAM=(∠EAF+∠BAF)﹣∠EAF=∠BAF,
∵BH∥CD,
∴∠BAF=∠AFG,
∴∠MAN=∠AFG.
20.解:(1)由MQ∥CD,得到∠1=∠3,∠2=∠4,其依据为:两直线平行,内错角相等;
由FM平分∠EFD,HM平分∠BHP,得到∠1=∠BHP,∠2=∠DFP,其依据为:角平分线定义.
故答案为:两直线平行,内错角相等;角平分线定义.
(2)如图2,∵HP⊥EF,
∴∠HPE=90°,
∴∠EHP+∠HEP=180°﹣90°=90°(三角形的内角和等于180°)
又∵AB∥CD,
∴∠HEP=∠DFP.
∴∠EHP+∠DFP=90°.
由(1)得:∠HMF=(∠EHP+∠DFP)=×90°=45°.
(3)如图3,∵NQ⊥FM,
∴∠NFQ+∠FNQ=180°﹣90°=90°(三角形的内角和等于180°).
∴∠NFQ=90°﹣∠FNQ.
∵FN平分∠HFE,FM平分∠EFD,
又∵∠NFQ=∠NFE+∠QFE=(∠HFE+∠EFD)=∠HFD,
∴∠HFD=2∠NFQ.
又∵AB∥CD,
∴∠EHF+∠HFD=180°,
∴∠EHF=180°﹣∠HFD=180°﹣2∠NFQ=180°﹣2(90°﹣∠FNQ)=2∠FNQ,
即无论点H在何处都有∠EHF=2∠FNQ.
21.解:(1)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°
∴∠EFD=∠BEF+30°=90°;
故答案为:90°;
(2)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°,
∴∠EFD=∠BEF+30°;
(3)如图2,过点F作FH∥EP,
由(2)知,∠EFD=∠BEF+30°,
设∠BEF=2x°,则∠EFD=(2x+30)°,
∵EP平分∠BEF,GF平分∠EFD,
∴∠PEF=∠BEF=x°,∠EFG=∠EFD=(x+15)°,
∵FH∥EP,
∴∠PEF=∠EFH=x°,∠P=∠HFG,
∵∠HFG=∠EFG﹣∠EFH=15°,
∴∠P=15°.
22.解:(1)如图1,
过点E作ER∥AB,
∵AB∥CD,
∴ER∥CD,
∵∠DCF=25°,∠E=20°,
∵CF平分∠ECD,∴∠DCF=∠FCE=25°,
∴∠CER=∠DCE=2∠DCF=50°,
∴∠BER=∠CER﹣∠CEB=30°,
∴∠ABE=∠BER=30°
答:∠ABE的度数为30°.
(2)如图2,分别过点E、F作AB的平行线ET、FL,
∵∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,
设∠ABF=α,则∠EBF=2α,
∴∠ABE=3α,∴∠BET=∠ABE=3α,
设∠CEB=β,
则∠DCE=∠CET=∠CEB+∠BET=3α+β,
∵CF平分∠ECD,
∴∠DCF=∠FCE=,
∴∠CFL=,∠BFL=∠ABF=α,
∴∠CFB=∠CFL﹣∠BFL=,
∴2×+180﹣β=190,
∴α=10,
∴∠ABE=30°.
答:∠ABE的度数为30°.
(3)如图3,过点P作PJ∥AB,
∵AB∥CD,
∴PJ∥CD,
∵PK平分∠BPH,
∴∠KPH=∠KPB=x,
∵HN∥PK,
∴∠NHP=x,
设∠MHN=y,
∴∠MHP=x+y,
∵HM平分∠DHP,
∴∠DHM=∠MHP=x+y,
∵∠DHQ=2∠DHN,
∴∠DHQ=2(x+y+y)=2x+4y,
∴∠PHQ=∠DHQ﹣∠DHP=(2x+4y)﹣(2x+2y)=2y,
∴∠HPJ=∠DHP=2x+2y,
∴∠BPJ=∠ABE=30°=2y,
∴∠PHQ=30°
答:∠PHQ的度数为30°.
23.解:(1)如图,延长DE交AB于H,
∵AB∥CD,
∴∠D=∠AHE=40°,
∵∠AED是△AEH的外角,
∴∠AED=∠A+∠AHE=30°+40°=70°,
故答案为:70;
(2)∠EAF=∠AED+∠EDG.
理由:∵AB∥CD,
∴∠EAF=∠EHC,
∵∠EHC是△DEH的外角,
∴∠EHG=∠AED+∠EDG,
∴∠EAF=∠AED+∠EDG;
(3)∵∠EAI:∠BAI=1:2,
∴设∠EAI=α,则∠BAE=3α,
∵∠AED=22°,∠I=20°,∠DKE=∠AKI,
又∵∠EDK+∠DKE+∠DEK=180°,∠KAI+∠KIA+∠AKI=180°,
∴∠EDK=α﹣2°,
∵DI平分∠EDC,
∴∠CDE=2∠EDK=2α﹣4°,
∵AB∥CD,
∴∠EHC=∠EAF=∠AED+∠EDG,
即3α=22°+2α﹣4°,
解得α=18°,
∴∠EDK=16°,
∴在△DKE中,∠EKD=180°﹣16°﹣22°=142°.
24.解:(1)如图1,延长EP交CD于M,
∵AB∥CD,
∴∠AEP=∠GMP,
∵∠EPG是△PGM的外角,
∴∠EPG=∠PMG+∠PGC=∠AEP+∠PGC;
(2)如图1,连接EG,
∵GE平分∠PEF,
∴∠PEG=∠FEG,
设∠AEP=α,∠PGC=β,则∠PGE=110°﹣α,∠EFG=2β,
∵AE∥CG,∠AEP+∠PGE=110°,
∴∠PEG+∠PGC=180°﹣110°=70°,即∠PEG=70°﹣β,
∵∠CGE是△EFG的外角,
∴∠FEG=∠CGE﹣∠EFG=β+(110°﹣α)﹣2β=110°﹣α﹣β,
70°﹣β=110°﹣α﹣β,
解得α=40°,
∴∠AEP=40°;
(3)如图2,∵EF平分∠PEB,
∴可设∠BEF=∠PEF=α,
∵AB∥CD,
∴∠GFE=∠BEF=α,
∴四边形PGFE中,∠PGF=360°﹣∠P﹣2α,
∴∠PGC=180°﹣(360°﹣∠P﹣2α)=∠P+2α﹣180°,
∵∠EFG是△FGH的外角,
∴∠FGH=∠EFG﹣∠EHG=α﹣∠EHG,
又∵QG平分∠PGC,
∴∠PGC=2∠FGH,
即∠P+2α﹣180°=2(α﹣∠EHG),
整理可得,∠P+2∠EHG=180°.
故答案为:∠P+2∠EHG=180°.
25.解:(1)如图1,∵DE、DF分别是∠CDO、∠CDB的平分线,
∴∠CDF=∠CDB,∠CDE=∠CDO,
∴∠EDF=(∠CDB+∠CDO)=90°,
又∵DF∥AO,
∴∠AED=90°,
∴DE⊥AO;
(2)如图2,连接OC,
∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠CDB是△COD的外角,∠AEC是△COE的外角,
∴∠CDB=∠COD+∠OCD,∠AEC=∠EOC+∠ECO,
∴∠CDB+∠AEC=∠COD+∠OCD+∠EOC+∠ECO=2∠DCE;
(3)图3中,∠CDB=∠AEC+2∠DCE;图4中,∠AEC=∠CDB+2∠DCE.理由:
如图3,∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠CDB是△ODG的外角,
∴∠CDB=∠DOG+∠DGO,
∵∠DGO是△CEG的外角,
∴∠DGO=∠AEC+∠C,
∴∠CDB=∠DOG+∠AEC+∠C=∠AEC+2∠DCE;
如图4,∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠AEC是△OEH的外角,
∴∠AEC=∠DOE+∠OHE,
∵∠OHE是△CDH的外角,
∴∠OHE=∠CDB+∠C,
∴∠AEC=∠DOE+∠CDB+∠C=∠CDB+2∠DCE.
26.解:(1)如图1,∵OP∥AE,
∴∠A=∠1,
∵∠BOP=58°,OB是∠AOP的角平分线,
∴∠AOP=2∠BOP=116°
∴∠1=180°﹣116°=64°,
∴∠A=∠1=64°;
(2)如图2,
∵OP∥AE,
∴∠POD=∠ADO=39°,
∵OB平分∠AOC,
∴∠AOB=∠BOC,
∵OD平分∠COP,
∴∠COP=2∠DOP=78°,
∴∠ABO﹣∠AOB=∠COP=78°;
(3)如图3,由(1)可知,∠ABO=(180°﹣m),∠AB1O=(180°﹣∠OBB1)=∠ABO=(180°﹣m),∠AB2O=(180°﹣m),…
则∠ABnO=.
27.解:(1)如图,设FG与NE交点为H点,AB与NE的交点I,
在△HNG中,∵∠G+∠HNG+∠NHG=180°
∴∠HNG=∠AIE=∠IHM+∠IMH=(∠E+∠EMF)+∠IMH=∠E+(∠EMF+∠IMH
)=∠E+∠AME
∠NHG=∠IHM=∠E+∠EMF=∠E+∠AME
∴∠G+∠HNG+∠NHG=∠G+(∠E+∠AME)+(∠E+∠AME)=180°
(∠G+2∠E)+∠AME=180°,即90°+∠AME=180°,
∴∠AME=60°;
(2)∠JPQ的度数不改变,
∵PQ平分∠MPN,NH平分∠PNC,
∴∠JPQ=∠JPN﹣∠MPN
=(∠ENC﹣∠MPN)
=(∠AOE﹣∠MPN)
=∠AME
=30°.
28.解:∵AD∥EF,
∴∠2=∠DAC,
∵∠1=∠2,
∴∠1=∠DAC,
∴∠GD∥AC,
∴∠BAG=∠C,
∵∠BAC=80°,∠B=∠C,
∴2∠C=180°﹣∠BAC=100°,
∴∠C=50°,
∴∠BDG=50°.
29.解:(1)∵AB∥CD,∠CDE=50°,
∴∠BED=∠CDE=50°,
∵EG平分∠DEB,
∴∠DEG=25°,
∵∠F=25°,
∴∠F=∠DEG=25°,
∴BF∥EG,
∵FB⊥BD,
∴EG⊥BD;
(2)由(1)得∠FBE=∠BEG=25°,
∵∠FBD=90°,
∴∠EBD=65°,
∵AB∥CD,
∴∠CDB=115°.
30.解:(1)∵射线CD∥AB,∠C=110°,
∴∠CAB=70°,∠BAD=∠EAD,
∵∠EAD=∠EDA,
∴∠EAD=∠BAD=∠EAB.
∵AF平分∠CAE,
∴∠FAD=∠FAE+∠EAD=∠CAB=×70°=35°;
(2)不变.
∵AB∥CD,∠C=110°,
∴∠CAB=70°.
当BD向右平移时,∠EAD增大,∠CAB不变,
∵∠EAD=∠EDA,∠AEC=∠EAD+∠EDA,
∴∠ADC:∠AEC=1:2;
(3)存在.
设∠BAD=∠EAD=∠EDA=x°,
∵由(1)知∠FAD=35°,
∴∠AFC=x°+35°.
∵AB∥CD,∠ABD=110°,
∴∠BDC=70°,
∴∠ADB=70°﹣x°,
∵∠AFC=∠ADB,
∴x°+35°=70°﹣x°,解得x=17.5°,
∴∠ADB=70°﹣17.5°=52.5°.
31.证明:连接EF.
∵FG⊥AC,HE⊥AC,
∴∠FGC=∠HEC=90°.
∴FG∥HE(同位角相等,两直线平行).
∴∠3=∠4(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4,
即∠DEF=∠EFC.
∴DE∥BC(内错角相等,两直线平行).
故答案为:HE,同位角相等,两直线平行;4,两直线平行,内错角相等;∠1+∠3,DEF,内错角相等,两直线平行.
32.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠EGF=∠AEG+∠GFC;
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
33.(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠BCF+∠ADE=180°.
∴∠BCF+∠B=180°.
∴CF∥AB;
(2)解:如图2,过点E作EK∥AB,
∴∠BEK=∠ABE=40°,
∵CF∥AB,
∴CF∥EK,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
(3)∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=7:13,
∴设∠EBC=7x°,则∠ECB=13x°,
∵DE∥BC,
∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,
∵∠AED+∠DEB+∠BEC=180°,
∴13x+7x+100=180,
解得x=4,
∴∠EBC=7x°=28°,
∵∠EBG=∠EBC+∠CBG,
∴∠CBG=∠EBG﹣∠EBC=40°﹣28°=12°.
34.(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFE=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90﹣x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
35.证明:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°
∴∠ADF=∠BCF(同角的补角相等)
∴AD∥BC(同位角相等,两直线平行)
∵BE平分∠ABC
∴∠ABC=2∠ABE(角平分线定义)
又∵∠ABC=2∠E
∴∠ABE=∠E
∴AB∥EF(内错角相等,两直线平行)
∵AD∥BC
∴∠BAD+∠ABC=180°(两直线平行,同旁内角互补)
BE平分∠ABC,AE平分∠BAD
∴∠ABE=∠ABC,∠BAF=∠BAD
∴∠ABE+∠BAF=∠ABC+∠BAD=×180°=90°
∵AB∥EF(己证)
∴∠BAF=∠F(两直线平行,内错角相等)
∠ABE=∠E
∴∠E+∠F=90°(等量代换)
36.解:(1)AD∥EF,
理由:∵∠BDA+∠CEG=180°,∠BDA+∠CDA=180°,
∴∠CEG=∠CDA,
∴AD∥EF;
(2)AD平分∠BAC,
理由:∵∠EDH=∠C,
∴DH∥AC,
∴∠H=∠EGC,
∵∠F=∠H,
∴∠F=∠EGC,
∵AD∥EF,
∴∠BAD=∠F,∠CAD=∠EGC,
∴∠BAD=∠CAD,
∴AD平分∠BAC.
37.(1)解:∵AD∥BE,
∴∠CAD=∠3,
∵∠2+∠CAE=∠CAD,∠3=80°,
∴∠2+∠CAE=80°,
∵∠2=30°,
∴∠CAE=50°;
(2)证明:∵∠2+∠CAE=∠CAD=∠3,
∠1=∠2,∠3=∠4,
∴∠1+∠CAE=∠4,
即∠BAE=∠4,
∴AB∥DC.
38.解:(1)证明:∵∠BDA+∠CEG=180°,∠BDA+∠ADC=180°.
∴∠ADC=∠CEG,
∴AD∥EF;
(2)∠BAD和∠CAD相等,理由如下:
∵∠EDH=∠C,
∴DH∥AC,
∴∠H=∠CGH,
∵∠CGH=∠AGF,
∴∠H=∠AGF,
∵∠F=∠H,
∴∠F=∠AGF,
∵AD∥EF,
∴∠BAD=∠F,∠CAD=∠AGF,
∴∠BAD=∠CAD;
(3)∵FH⊥BC,
∴∠CEG=90°,
∵∠C=30°,
∴∠CGE=90°﹣30°=60°,
∴∠F=∠AGF=∠CGE=60°.
39.(1)证明:∵∠A+∠3=180°,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠ABD=180°,
∴∠D+∠CBD+∠CBA=180°,
∵∠D=80°,∠CBD=70°,
∴∠CBA=180°﹣∠D﹣∠CBD
=180°﹣80°﹣70°
=30°.
40.解:(1)证明:∵FG∥AE,
∴∠FGC=∠2,
∵∠1=∠2,
∴∠1=∠FGC,
∴AB∥CD;
(2)∵AB∥CD,
∴∠ABC+∠D=180°,
∵∠D=112°,
∴∠ABD=180°﹣112°=68°,
∵BC平分∠ABD,
∴∠ABC=ABD=34°,
∵AB∥CD,
∴∠C=∠ABC=34°.
所以∠C的度数为34°
1.如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H.点F是边AB上一点.使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G,若∠DEH=100°,则∠BEG的度数为( )
A.30°
B.40°
C.50°
D.60°
2.已知直线AB∥CD,点P、Q分别在AB、CD上,如图所示,射线PB按顺时针方向以每秒4°的速度旋转至PA便立即回转,并不断往返旋转;射线QC按顺时针方向每秒1°旋转至QD停止,此时射线PB也停止旋转.
(1)若射线PB、QC同时开始旋转,当旋转时间30秒时,PB'与QC'的位置关系为
;
(2)若射线QC先转45秒,射线PB才开始转动,当射线PB旋转的时间为
秒时,PB′∥QC′.
3.如图,直线AB∥CD,直线EF与AB,CD分别交于点E,F,∠AEF与∠CFE的角平分线交于点P,延长FP交AB于点G,过点G作GQ⊥FG交直线EF于点Q,连接PQ,点M是QG延长线上的一点,且∠PQM=∠QPM,若PN平分∠FPM交CD于点N,则∠NPQ的度数为
.
4.如图,已知AC∥BD,BC平分∠ABD,CE平分∠DCM,且BC⊥CE.则下列结论:①CB平分∠ACD,②AB∥CD,③∠A=∠BDC,④点P是线段BE上任意一点,则∠APM=∠BAP+∠PCD.正确的是
.
5.如图,∠AEM=∠DFN=a,∠EMN=∠MNF=b,∠PEM=∠AEM,∠MNP=∠FNP,∠BEP,∠NFD的角平分线交于点I,若∠I=∠P,则a和b的数量关系为
(用含a的式子表示b)
6.已知:如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=
.
7.光线在不间介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射,由于折射率相同,所以水在水中平行的光线,在空气中也是平行的,如图,已知EF∥AB∥CD,∠2=3∠3,∠8=2∠5+10°,则∠7﹣∠4的结果为
度.
8.在6×6的方格纸上,有7个格点已标记,分别为A,B,C,D,E,F,G.从中找出4个点,两个点连一条线,另外两点连一条线,使两条连线平行,则所构造的平行连线可记作:
.(格式如:MN∥PQ,用图中的字母表示)
9.如图,已知EF⊥AC于点F,DB⊥AC于点M.∠1=∠2,∠3=∠C,若∠ANM=70°,∠BAN的度数是
.
10.探照灯、汽车灯等很多灯具都与平行线有关,如图所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB、OC,经灯碗反射以后平行射出,其中∠ABO=30°,∠BOC=105°,则∠DCO的度数是
.
11.已知AB∥CD,点M在直线AB上,点N、Q在直线CD上,点P在直线AB、CD之间,∠AMP=∠PQN=α,PQ平分∠MPN.
(1)如图①,求∠MPQ的度数(用含α的式子表示);
(2)如图②,过点Q作QE∥PN交PM的延长线于点E,过E作EF平分∠PEQ交PQ于点F.请你判断EF与PQ的位置关系,并说明理由;
(3)如图③,在(2)的条件下,连接EN,若NE平分∠PNQ,请你判断∠NEF与∠AMP的数量关系,并说明理由.
12.已知,AE∥BD,∠A=∠D.
(1)如图1,求证:AB∥CD;
(2)如图2,作∠BAE的平分线交CD于点F,点G为AB上一点,连接FG,若∠CFG的平分线交线段AG于点H,求证:∠ECF+2∠AFH=∠E+2∠BHF;
(3)如图3,在(2)的条件下,连接AC,若∠ACE=∠BAC+∠BGM,过点H作HM⊥FH交FG的延长线于点M,且2∠E﹣3∠AFH=20°,求∠EAF+∠GMH的度数.
13.已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系
;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
14.如图1,E点在BC上,∠A=∠D,∠ACB+∠BED=180°.
(1)求证:AB∥CD;
(2)如图2,AB∥CD,BG平分∠ABE,与∠EDF的平分线交于H点,若∠DEB比∠DHB大60°,求∠DEB的度数.
(3)保特(2)中所求的∠DEB的度数不变,如图3,BM平分∠EBK,DN平分∠CDE,作BP∥DN,则∠PBM的度数是否改变?若不变,请求值;若改变,请说明理由.
15.如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.
(1)判断DE与BF是否平行?并说明理由;
(2)试说明:∠C=2∠P.
16.完成下面的解题过程:
如图,AD∥BC,点F是AD上一点,CF与BA的延长线相交于点E,且∠1=∠2,∠3=∠4.CD与BE平行吗?为什么?
解:CD∥BE,理由如下:
∵AD∥BC(已知),
∴∠4=
(
)
∵∠3=∠4(已知),
∴∠3=
(
)
∵∠1=∠2(已知),
∴∠1+∠ACE=∠2+∠ACE
(
)
即∠BCE=
∴∠3=
∴CD∥BE(
)
17.如图,取一副三角板按图1拼接,固定三角板ADE(含30°),将三角板ABC(含45°)绕点A顺时针方向旋转一个大小为α的角(0°<α≤45°),试问:
(1)当∠α=
度时,能使图2中的AB∥DE;
(2)当旋转到AB与AE重叠时(如图3),则∠α=
度;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;
(4)当0°<α≤45°时,连接BD(如图4),探求∠DBC+∠CAE+∠BDE的值的大小变化情况,并说明理由.
18.如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
(1)求证:EM∥NG;
(2)连接EG,在GN上取一点H,使∠HEG=∠HGE,作∠FEH的平分线EP交AB于点P,求∠PEG的度数.
19.如图1,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠DCE﹣∠HAE=90°.(1)求证:BH∥CD.
(2)如图2:直线AF交DC于F,AM平分∠EAF,AN平分∠BAE.试探究∠MAN,∠AFG的数量关系.
20.如图,已知直线AB∥CD,直线EF分别与AB、CD相交于点E、F,FM平分∠EFD,点H是射线EA上一动点(不与点E重合),过点H的直线交EF于点P,HM平分∠BHP交FM于点M.
(1)如图1,试说明:∠HMF=(∠BHP+∠DFP);
请在下列解答中,填写相应的理由:
解:过点M作MQ∥AB(过直线外一点有且只有一条直线与这条直线平行).
∵AB∥CD(已知),
∴MQ∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠1=∠3,∠2=∠4(
)
∴∠1+∠2=∠3+∠4(等式的性质)
即∠HMF=∠1+∠2.
∵FM平分∠EFD,HM平分∠BHP(已知)
∵∠1=∠BHP,∠2=∠DFP(
)
∴∠HMF=∠BHP+∠DFP=(∠BHP+∠DFP)(等量代换).
(2)如图2,若HP⊥EF,求∠HMF的度数;
(3)如图3,当点P与点F重合时,FN平分∠HFE交AB于点N,过点N作NQ⊥FM于点Q,试说明无论点H在何处都有∠EHF=2∠FNQ.
21.如图1,已知AB∥CD,∠B=30°,∠D=120°;
(1)若∠E=60°,则∠F=
;
(2)请探索∠E与∠F之间满足的数量关系?说明理由;
(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
22.已知,AB∥CD,CF平分∠ECD.
(1)如图1,若∠DCF=25°,∠E=20°,求∠ABE的度数.
(2)如图2,若∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,求∠ABE的度数.
(3)如图3,在(2)的条件下,P为射线BE上一点,H为CD上一点,PK平分∠BPH,HN∥PK,HM平分∠DHP,∠DHQ=2∠DHN,求∠PHQ的度数.
23.已知,AB∥CD,点E为射线FG上一点.
(1)如图1,若∠EAF=30°,∠EDG=40°,则∠AED=
°;
(2)如图2,当点E在FG延长线上时,此时CD与AE交于点H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图3,DI平分∠EDC,交AE于点K,交AI于点I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD的度数.
24.如图1,AB∥CD,直线EF交AB于点E,交CD于点F,点G在CD上,点P在直线EF左侧、且在直线AB和CD之间,连接PE、PG.
(1)求证:∠EPG=∠AEP+∠PGC;
(2)连接EG,若EG平分∠PEF,∠AEP+∠PGE=110°,∠PGC=∠EFC,求∠AEP的度数;
(3)如图2,若EF平分∠PEB,∠PGC的平分线所在的直线与EF相交于点H,则∠EPG与∠EHG之间的数量关系为
.
25.已知E、D分别在∠AOB的边OA、OB上,C为平面内一点,DE、DF分别是∠CDO、∠CDB的平分线.
(1)如图1,若点C在OA上,且FD∥AO,求证:DE⊥AO;
(2)如图2,若点C在∠AOB的内部,且∠DEO=∠DEC,请猜想∠DCE、∠AEC、∠CDB之间的数量关系,并证明;
(3)若点C在∠AOB的外部,且∠DEO=∠DEC,请根据图3、图4分别写出∠DCE、∠AEC、∠CDB之间的数量关系(不需证明).
26.已知:射线OP∥AE
(1)如图1,∠AOP的角平分线交射线AE与点B,若∠BOP=58°,求∠A的度数.
(2)如图2,若点C在射线AE上,OB平分∠AOC交AE于点B,OD平分∠COP交AE于点D,∠ADO=39°,求∠ABO﹣∠AOB的度数.
(3)如图3,若∠A=m,依次作出∠AOP的角平分线OB,∠BOP的角平分线OB1,∠B1OP的角平分线OB2,∠Bn﹣1OP的角平分线OBn,其中点B,B1,B2,…,Bn﹣1,Bn都在射线AE上,试求∠ABnO的度数.
27.(1)如图1,已知直线AB∥CD,点E是AB上方一点,MF平分∠AME,若点G恰好在MF的反向延长线上,且NE平分∠CNG,2∠E与∠G互余,求∠AME的大小.
(2)如图2,在(1)的条件下,若点P是EM上一动点,PQ平分∠MPN,NH平分∠PNC,交AB于点H,PJ∥NH,当点P在线段EM上运动时,∠JPQ的度数是否改变?若不变,求出其值;若改变,请说明你的理由.
28.如图,在△ABC中,∠B=∠C,∠BAC=80°,AD∥EF,∠1=∠2,求∠BDG的度数.
29.如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=50°,∠F=25°.
(1)求证:EG⊥BD;
(2)求∠CDB的度数.
30.如图,已知射线CD∥AB,∠C=∠ABD=110°,E,F在CD上,且满足∠EAD=∠EDA,AF平分∠CAE.
(1)求∠FAD的度数;
(2)若向右平行移动BD,其它条件不变,那么∠ADC:∠AEC的值是否发生变化?若变化,找出其中规律;若不变,求出这个比值;
(3)在向右平行移动BD的过程中,是否存在某种情况,使∠AFC=∠ADB?若存在,请求出∠ADB度数;若不存在,说明理由.
31.请将下列题目的证明过程补充完整:
如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2,求证:DE∥BC.
证明:连接EF.
∵FG⊥AC,HE⊥AC,
∴∠FGC=∠HEC=90°.
∴FG∥
(
).
∴∠3=∠
(
).
又∵∠1=∠2,
∴
=∠2+∠4,
即∠
=∠EFC.
∴DE∥BC(
).
32.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.
33.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图1,求证:CF∥AB;
(2)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(3)如图3,在(2)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=7:13,BE平分∠ABG,求∠CBG的度数.
34.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
35.如图:已知:∠ADE+∠BCF=180°,BE平分∠ABC交CD的延长线于点E,AF平分∠BAD交DC的延长线于点F,若∠ABC=2∠E,则∠E+∠F=90°,完成下列推理过程.
证明:
∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°
∴∠ADF=∠BCF(
)
∴AD∥BC(
)
∵BE平分∠ABC
∴∠ABC=2∠ABE(
)
又∵∠ABC=2∠E
∴∠ABE=∠E
∴AB∥EF(
)
∵AD∥BC
∴∠BAD+∠ABC=180°(
)
∵BE平分∠ABC,AF平分∠BAD
∴∠ABE=∠ABC,∠BAF=∠BAD
∴∠ABE+∠BAF=∠ABC+∠BAD=×180°=90°
∵AB∥EF(
)
∴∠BAF=∠F(
)
∵∠ABE=∠E
∴∠E+∠F=90°(
)
36.如图,点D为线段BC上的一点,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,那么AD平分∠BAC吗?请说明理由.
37.如图,AF的延长线与BC的延长线交于点E,AD∥BE,∠1=∠2=30°,∠3=∠4=80°.
(1)求∠CAE的度数;
(2)求证:AB∥DC.
38.如图,AD交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)证明AD∥EF;
(2)若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,则∠BAD和∠CAD相等吗?请说明理由;
(3)在(2)的条件下,若FH⊥BC,∠C=30°,求∠F的度数.
39.如图,已知∠A+∠3=180°,∠1=∠2,∠D=80°,∠CBD=70°.
(1)试说明AB∥CD;
(2)求∠CBA的度数.
40.如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.
(1)求证:AB∥CD;
(2)若BC平分∠ABD,∠D=112°,求∠C的度数.
参考答案
1.解:设FBE=∠FEB=α,则∠AFE=2α,
∠FEH的角平分线为EG,设∠GEH=∠GEF=β,
∵AD∥BC,∴∠ABC+∠BAD=180°,
而∠D=∠ABC,∴∠D+∠BAD=180°,∴AB∥CD,
∠DEH=100°,则∠CEH=∠FAE=80°,
∠AEF=180°﹣∠FEG﹣∠HEG=180°﹣2β,
在△AEF中,
在△AEF中,80°+2α+180﹣2β=180°
故β﹣α=40°,
而∠BEG=∠FEG﹣∠FEB=β﹣α=40°,
故选:B.
2.解:(1)如图1,当旋转时间30秒时,由已知得∠BPB′=4°×30=120°,∠CQC′=30°,
过E作EF∥AB,则EF∥CD,
∴∠PEF=180°﹣∠BPB′=60°,∠QEF=∠CQC′=30°,
∴∠PEQ=90°,
∴PB′⊥QC′,
故答案为:PB′⊥QC′;
(2)①当0s<t≤45时,如图2,则∠BPB′=4t°,∠CQC′=45°+t°,
∵AB∥CD,PB′∥QC′,
∴∠BPB′=∠PEC=∠CQC′,
即4t=45+t,
解得,t=15(s);
②当45s<t≤67.5s时,如图3,则∠APB′=4t﹣180°,∠CQC'=t+45°,
∵AB∥CD,PB′∥QC′,
∴∠APB′=∠PED=180°﹣∠CQC′,
即4t﹣180=180﹣(45+t),
解得,t=63(s);
③当67.5s<t<135s时,如图4,则∠BPB′=4t﹣360°,∠CQC′=t+45°,
∵AB∥CD,PB′∥QC′,
∴∠BPB′=∠PEC=∠CQC′,
即4t﹣360=t+45,
解得,t=135(s);
综上,当射线PB旋转的时间为15秒或63秒或135秒时,PB′∥QC′.
故答案为:15秒或63秒或135秒.
3.解:设∠PQM=∠QPM=x°,
∵PN平分∠MPF,
∴∠MPN=∠FPN,
设∠MPN=∠FPN=y°,
∵∠AEF与∠CFE的角平分线交于点P,
∴∠PEF=,∠EFP=,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴∠PEF+∠PFE==90°,
∴∠EPF=180°﹣(∠PEF+∠PFE)=180°﹣90°=90°,
∵GQ⊥PF,
∴∠QGP=90°,
∴∠QGP=∠EPF,
∴GQ∥EP,
∴∠PQM=∠QPE=x°,
∵∠QPE+∠QPM+∠FPN+∠NPM+∠EPF=360°,
∴x+x+y+y+90=360,
∴x+y=135,
即∠QPM+∠NPM=135°,
∴∠NPQ=∠QPM+∠NPM=135°.
4.解:如图,
∵AC∥BD,
∵∠2=∠3
∵BC平分∠ABD,
∴∠1=∠2,
∴∠1=∠3,
∵CE平分∠DCM,
∴∠4=∠5,
∵BC⊥CE.
∴∠4+∠6=90°,
∴∠5+∠6=90°,
∵∠3+∠5=90°,
∴∠3=∠6,
∴CB平分∠ACD,故①正确;
∴∠1=∠6,
AB∥CD,故②正确;
∴四边形ABCD是平行四边形,
∴∠A=∠BDC,故③正确;
如图,点P是线段BE上任意一点,
∵AB与PC不平行,CD与PM不平行,
∴∠BAP≠∠APC,∠PCD≠∠CPM,
∴∠APM≠∠BAP+∠PCD.故④不正确.
所以正确的是①②③.
故答案为:①②③.
5.解:分别过点P、I作ME∥PH,AB∥GI,
设∠AEM=2x,∠PNF=2y,则∠PEM=x,∠MNP=y,
∴∠DFN=2x,
∵PH∥ME,
∴∠EPH=x,
∵EM∥FN,
∴PH∥FN,
∴∠HPN=2y,∠EPN=x+2y,
同理,∠EIF=,
∵∠EPN=∠EIF,
∴=x+2y,
∴,
∴,
故答案为:.
6.解:∵∠1+∠2=180°,∠1+∠BDC=180°
∴∠2=∠BDC
∴EF∥AB
∴∠3=∠BDE
∵∠3=∠A
∴∠A=∠BDE
∴AC∥DE
∴∠ACB+∠CED=180°
∵CD平分∠ACB,∠4=35°
∴∠ACB=2∠4=2×35°=70°
∴∠CED=180°﹣∠ACB=180°﹣70°=110°
故答案为:110°.
7.解:∵EF∥AB∥CD,
∴∠4=∠2,∠5=∠6,∠7=∠8,∠4+∠6=180°,∠3+∠8=180°,
∴∠4=180°﹣∠6,∠3=180°﹣∠8=180°﹣∠7,
∵∠2=3∠3,∠8=2∠5+10°,
∴∠4=3∠3,∠7=2∠5+10°=2(180°﹣∠4)+10°=2(180°﹣3∠3)+10°=2[180°﹣3(180°﹣∠7)]+10°,
∴∠7=142°,
∴∠4=3∠3=3(180°﹣∠7)=114°,
∴∠7﹣∠4=28°,
故答案为:28.
8.解:如图所示,过A、G两点作直线AG,过C、F两点作直线CF,
根据方格的性质得出:∠1=∠2,
∵tan∠1==3,tan∠3==3,
∴∠1=∠3,
∴∠2=∠3,
∴AG∥CF,
故答案为:AG∥CF.
9.解:∵EF⊥AC,DB⊥AC,
∴∠EFC=∠DMC=90°,
∴BD∥FE,
∴∠2=∠BDC,
∵∠1=∠2,
∴∠1=∠BDC,
∴MN∥CD,
∵∠3=∠C,
∴AB∥CD,
∴MN∥AB,
∴∠BAN+∠ANM=180°,
∵∠ANM=70°,
∴∠BAN=110°,
故答案为:110°.
10.解:过O点作OH∥AB,则∠ABO=∠HOB=30°,
∵∠BOC=105°,
∴∠HOC=105°﹣30°=75°,
∵AB∥CD,
∴OH∥CD,
∴∠HOC=∠DCO=75°.
故答案为:75°.
11.解:(1)如图①,过点P作PR∥AB,
∵AB∥CD,
∴AB∥CD∥PR,
∴∠AMP=∠MPR=α,∠PQN=∠RPQ=α,
∴∠MPQ=∠MPR+∠RPQ=2α;
(2)如图②,EF⊥PQ,理由如下:
∵PQ平分∠MPN.
∴∠MPQ=∠NPQ=2α,
∵QE∥PN,
∴∠EQP=∠NPQ=2α,
∴∠EPQ=∠EQP=2α,
∵EF平分∠PEQ,
∴∠PEQ=2∠PEF=2∠QEF,
∵∠EPQ+∠EQP+∠PEQ=180°,
∴2∠EPQ+2∠PEF=180°,
∴∠EPQ+∠PEF=90°,
∴∠PFE=180°﹣90°=90°,
∴EF⊥PQ;
(3)如图③,∠NEF=∠AMP,理由如下:
由(2)可知:∠EQP=2α,∠EFQ=90°,
∴∠QEF=90°﹣2α,
∵∠PQN=α,
∴∠NQE=∠PQN+∠EQP=3α,
∵NE平分∠PNQ,
∴∠PNE=∠QNE,
∵QE∥PN,
∴∠QEN=∠PNE,
∴∠QNE=∠QEN,
∵∠NQE=3α,
∴∠QNE=(180°﹣∠NQE)=(180°﹣3α),
∴∠NEF=180°﹣∠QEF﹣∠NQE﹣∠QNE
=180°﹣(90°﹣2α)﹣3α﹣(180°﹣3α)
=180°﹣90°+2α﹣3α﹣90°+α
=α
=∠AMP.
∴∠NEF=∠∠AMP.
12.(1)证明:∵AE∥BD,
∴∠A+∠B=180°,
∵∠A=∠D,
∴∠D+∠B=180°,
∴AB∥CD;
(2)证明:如图2,过点E作EP∥CD,
∵AB∥CD,
∴AB∥EP,
∴∠PEA=∠EAB,∠PEC=∠ECF,
∵∠AEC=∠PEC﹣∠PEA,
∴∠AEC=∠ECF﹣∠EAB,
即∠ECF=∠AEC+∠EAB,
∵AF是∠BAE的平分线,
∴∠EAF=∠FAB=EAB,
∵FH是∠CFG的平分线,
∴∠CFH=∠HFG=CFG,
∵CD∥AB,
∴∠BHF=∠CFH,∠CFA=∠FAB,
设∠FAB=α,∠CFH=β,
∵∠AFH=∠CFH﹣∠CFA=∠CFH﹣∠FAB,
∴∠AFH=β﹣α,∠BHF=∠CFH=β,
∴∠ECF+2∠AFH=∠AEC+∠EAB+2∠AFH=∠AEC+2α+2(β﹣α)=∠AEC+2β,
∴∠ECF+2∠AFH=∠E+2∠BHF;
(3)解:如图,延长DC至点Q,
∵AB∥CD,
∴∠QCA=∠CAB,∠BGM=∠DFG,∠CFH=∠BHF,∠CFA=∠FAG,
∵∠ACE=∠BAC+∠BGM,
∴∠ECQ+∠QCA=∠BAC+∠BGM,
∴∠ECQ=∠BGM=∠DFG,
∵∠ECQ+∠ECD=180°,∠DFG+∠CFG=180°,
∴∠ECF=∠CFG,
由(2)问知:∠ECF+2∠AFH=∠AEC+2∠BHF,∠CFG=2∠CFH=2∠BHF,
∴∠AEC=2∠AFH,
∵2∠AEC﹣3∠AFH=20°,
∴∠AFH=20°,
由(2)问知:∠CFM=2β,∠FHG=β,
∵FH⊥HM,
∴∠FHM=90°,
∴∠GHM=90°﹣β,
过点M作MN∥AB,
∴MN∥CD,
∴∠CFM+∠NMF=180°,∠GHM=∠HMN=90°﹣β,
∴∠HMB=∠HMN=90°﹣β,
由(2)问知:∠EAF=∠FAB,
∴∠EAF=∠CFA=∠CFH﹣∠AFH=β﹣20°,
∴∠EAF+∠GMH=β﹣20°+90°﹣β=70°,
∴∠EAF+∠GMH=70°.
13.解:(1)如图1,AM与BC的交点记作点O,
∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°,
故答案为:∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,BG∥AM,
∴CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
14.(1)证明:如图1,延长DE交AB于点F,
∵∠ACB+∠BED=180°,∠CED+∠BED=180°,
∴∠ACB=∠CED,
∴AC∥DF,
∴∠A=∠DFB,
∵∠A=∠D,
∴∠DFB=∠D,
∴AB∥CD;
(2)如图2,作EM∥CD,HN∥CD,
∵AB∥CD,
∴AB∥EM∥HN∥CD,
∴∠1+∠EDF=180°,∠MEB=∠ABE,
∵BG平分∠ABE,
∴∠ABG=ABE,
∵AB∥HN,
∴∠2=∠ABG,
∵CF∥HN,
∴∠2+∠β=∠3,
∴ABE+∠β=∠3,
∵DH平分∠EDF,
∴∠3=EDF,
∴ABE+∠β=EDF,
∴∠β=(∠EDF﹣∠ABE),
∴∠EDF﹣∠ABE=2∠β,
设∠DEB=∠α,
∵∠α=∠1+∠MEB=180°﹣∠EDF+∠ABE=180°﹣(∠EDF﹣∠ABE)=180°﹣2∠β,
∵∠DEB比∠DHB大60°,
∴∠α﹣60°=∠β,
∴∠α=180°﹣2(∠α﹣60°)
解得∠α=100°
∴∠DEB的度数为100°;
(3)∠PBM的度数不变,理由如下:
如图3,过点E作ES∥CD,设直线DF和直线BP相交于点G,
∵BM平分∠EBK,DN平分∠CDE,
∴∠EBM=∠MBK=EBK,
∠CDN=∠EDN=CDE,
∵ES∥CD,AB∥CD,
∴ES∥AB∥CD,
∴∠DES=∠CDE,
∠BES=∠ABE=180°﹣∠EBK,
∠G=∠PBK,
由(2)可知:∠DEB=100°,
∴∠CDE+180°﹣∠EBK=100°,
∴∠EBK﹣∠CDE=80°,
∵BP∥DN,
∴∠CDN=∠G,
∴∠PBK=∠G=∠CDN=CDE,
∴∠PBM=∠MBK﹣∠PBK
=∠EBK﹣CDE
=(∠EBK﹣∠CDE)
=80°
=40°.
15.解:(1)DE∥BF,
理由是:∵∠3=∠4,
∴BD∥CE,
∴∠5=∠FAB,
∵∠5=∠C,
∴∠C=∠FAB,
∴AB∥CD,
∴∠2=∠BGD,
∵∠1=∠2,
∴∠1=∠BGD,
∴DE∥BF;
(2)∵AB∥CD,
∴∠P=∠PDH,
∵DP平分∠BDH,
∴∠BDP=∠PDH,
∴∠BDP=∠PDH=∠P,
∵∠5=∠P+∠BDP,
∴∠5=2∠P,
∵∠C=∠5,
∴∠C=2∠P.
16.解:CD∥BE,理由如下:
∵AD∥BC(已知),
∴∠4=∠BCE(两直线平行,同位角相等)
∵∠3=∠4(已知),
∴∠3=∠BCE(等量代换)
∵∠1=∠2(已知),
∴∠1+∠ACE=∠2+∠ACE
(等式性质)
即∠BCE=∠ACD
∴∠3=∠ACD
∴CD∥BE(内错角相等,两直线平行)
故答案为:∠BCE;两直线平行,同位角相等;∠BCE;等量代换;等式性质;∠ACD;∠ACD;内错角相等,两直线平行.
17.解:(1)如图2,当AB∥DE时,∠BAE=∠E=30°,
∵∠BAC=45°,
∴∠CAE=45°﹣30°=15°,
即∠α=15°,
故答案为:15;
(2)当旋转到AB与AE重叠时,∠α=∠BAC=45°,
故答案为:45;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,旋转角α的所有可能的度数为15°,45°.
①当AB∥DE时,α=15°;
②当AD∥CB时,α=45°;
③当DE∥BC时,α=105°;
④当AE∥BC时,α=135°;
⑤当AC∥DE时,α=150°.
又∵0°<α≤45°,
∴旋转角α的所有可能的度数为15°,45°.
(4)如图4,当0°<α≤45°时,∠DBC+∠CAE+∠BDE=105°,保持不变;
理由:设BD分别交AE、AC于点M、N,
在△AMN中,∠AMN+∠CAE+∠ANM=180°,
∵∠ANM=∠C+∠DBC,∠AMN=∠E+∠BDE,
∴∠E+∠BDE+∠CAE+∠C+∠DBC=180°,
∵∠E=30°,∠C=45°,
∴∠DBC+∠CAE+∠BDE=180°﹣75°=105°.
18.解:(1)∵AB∥CD,
∴∠AMN+∠CNM=180°,
∵ME,NE分别是∠AMN与∠CNM的平分线,
∴∠EMN=∠AMN,∠ENM=∠MNC,
∴∠EMN+∠ENM=90°,即∠MEN=90°,
又∵NG⊥EN,
∴∠MEN+∠ENH=180°,
∴EM∥NG;
(2)设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°﹣2x,
∵EP平分∠FEH,
∴∠FEH=2∠PEH=2(∠PEG+x),
又∵∠FEH+∠HEN=180°,
∴2(∠PEG+x)+90°﹣2x=180°,
解得∠PEG=45°.
19.(1)证明:如图,延长AE交DC于F,
∵AE⊥CE,
∴∠CEF=90°,
根据三角形的外角性质,∠DCE﹣∠AFD=∠CEF=90°,
又∵∠DCE﹣∠HAE=90°,
∴∠HAE=∠AFD,
∴BH∥CD;
(2)解:∵AM平分∠EAF,AN平分∠BAE,
∴∠EAM=∠EAF,∠EAN=∠BAE=(∠EAF+∠BAF),
∴∠MAN=∠EAN﹣∠EAM=(∠EAF+∠BAF)﹣∠EAF=∠BAF,
∵BH∥CD,
∴∠BAF=∠AFG,
∴∠MAN=∠AFG.
20.解:(1)由MQ∥CD,得到∠1=∠3,∠2=∠4,其依据为:两直线平行,内错角相等;
由FM平分∠EFD,HM平分∠BHP,得到∠1=∠BHP,∠2=∠DFP,其依据为:角平分线定义.
故答案为:两直线平行,内错角相等;角平分线定义.
(2)如图2,∵HP⊥EF,
∴∠HPE=90°,
∴∠EHP+∠HEP=180°﹣90°=90°(三角形的内角和等于180°)
又∵AB∥CD,
∴∠HEP=∠DFP.
∴∠EHP+∠DFP=90°.
由(1)得:∠HMF=(∠EHP+∠DFP)=×90°=45°.
(3)如图3,∵NQ⊥FM,
∴∠NFQ+∠FNQ=180°﹣90°=90°(三角形的内角和等于180°).
∴∠NFQ=90°﹣∠FNQ.
∵FN平分∠HFE,FM平分∠EFD,
又∵∠NFQ=∠NFE+∠QFE=(∠HFE+∠EFD)=∠HFD,
∴∠HFD=2∠NFQ.
又∵AB∥CD,
∴∠EHF+∠HFD=180°,
∴∠EHF=180°﹣∠HFD=180°﹣2∠NFQ=180°﹣2(90°﹣∠FNQ)=2∠FNQ,
即无论点H在何处都有∠EHF=2∠FNQ.
21.解:(1)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°
∴∠EFD=∠BEF+30°=90°;
故答案为:90°;
(2)如图1,分别过点E,F作EM∥AB,FN∥AB,
∴EM∥AB∥FN,
∴∠B=∠BEM=30°,∠MEF=∠EFN,
又∵AB∥CD,AB∥FN,
∴CD∥FN,
∴∠D+∠DFN=180°,
又∵∠D=120°,
∴∠DFN=60°,
∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,
∴∠EFD=∠MEF+60°,
∴∠EFD=∠BEF+30°;
(3)如图2,过点F作FH∥EP,
由(2)知,∠EFD=∠BEF+30°,
设∠BEF=2x°,则∠EFD=(2x+30)°,
∵EP平分∠BEF,GF平分∠EFD,
∴∠PEF=∠BEF=x°,∠EFG=∠EFD=(x+15)°,
∵FH∥EP,
∴∠PEF=∠EFH=x°,∠P=∠HFG,
∵∠HFG=∠EFG﹣∠EFH=15°,
∴∠P=15°.
22.解:(1)如图1,
过点E作ER∥AB,
∵AB∥CD,
∴ER∥CD,
∵∠DCF=25°,∠E=20°,
∵CF平分∠ECD,∴∠DCF=∠FCE=25°,
∴∠CER=∠DCE=2∠DCF=50°,
∴∠BER=∠CER﹣∠CEB=30°,
∴∠ABE=∠BER=30°
答:∠ABE的度数为30°.
(2)如图2,分别过点E、F作AB的平行线ET、FL,
∵∠EBF=2∠ABF,∠CFB的2倍与∠CEB的补角的和为190°,
设∠ABF=α,则∠EBF=2α,
∴∠ABE=3α,∴∠BET=∠ABE=3α,
设∠CEB=β,
则∠DCE=∠CET=∠CEB+∠BET=3α+β,
∵CF平分∠ECD,
∴∠DCF=∠FCE=,
∴∠CFL=,∠BFL=∠ABF=α,
∴∠CFB=∠CFL﹣∠BFL=,
∴2×+180﹣β=190,
∴α=10,
∴∠ABE=30°.
答:∠ABE的度数为30°.
(3)如图3,过点P作PJ∥AB,
∵AB∥CD,
∴PJ∥CD,
∵PK平分∠BPH,
∴∠KPH=∠KPB=x,
∵HN∥PK,
∴∠NHP=x,
设∠MHN=y,
∴∠MHP=x+y,
∵HM平分∠DHP,
∴∠DHM=∠MHP=x+y,
∵∠DHQ=2∠DHN,
∴∠DHQ=2(x+y+y)=2x+4y,
∴∠PHQ=∠DHQ﹣∠DHP=(2x+4y)﹣(2x+2y)=2y,
∴∠HPJ=∠DHP=2x+2y,
∴∠BPJ=∠ABE=30°=2y,
∴∠PHQ=30°
答:∠PHQ的度数为30°.
23.解:(1)如图,延长DE交AB于H,
∵AB∥CD,
∴∠D=∠AHE=40°,
∵∠AED是△AEH的外角,
∴∠AED=∠A+∠AHE=30°+40°=70°,
故答案为:70;
(2)∠EAF=∠AED+∠EDG.
理由:∵AB∥CD,
∴∠EAF=∠EHC,
∵∠EHC是△DEH的外角,
∴∠EHG=∠AED+∠EDG,
∴∠EAF=∠AED+∠EDG;
(3)∵∠EAI:∠BAI=1:2,
∴设∠EAI=α,则∠BAE=3α,
∵∠AED=22°,∠I=20°,∠DKE=∠AKI,
又∵∠EDK+∠DKE+∠DEK=180°,∠KAI+∠KIA+∠AKI=180°,
∴∠EDK=α﹣2°,
∵DI平分∠EDC,
∴∠CDE=2∠EDK=2α﹣4°,
∵AB∥CD,
∴∠EHC=∠EAF=∠AED+∠EDG,
即3α=22°+2α﹣4°,
解得α=18°,
∴∠EDK=16°,
∴在△DKE中,∠EKD=180°﹣16°﹣22°=142°.
24.解:(1)如图1,延长EP交CD于M,
∵AB∥CD,
∴∠AEP=∠GMP,
∵∠EPG是△PGM的外角,
∴∠EPG=∠PMG+∠PGC=∠AEP+∠PGC;
(2)如图1,连接EG,
∵GE平分∠PEF,
∴∠PEG=∠FEG,
设∠AEP=α,∠PGC=β,则∠PGE=110°﹣α,∠EFG=2β,
∵AE∥CG,∠AEP+∠PGE=110°,
∴∠PEG+∠PGC=180°﹣110°=70°,即∠PEG=70°﹣β,
∵∠CGE是△EFG的外角,
∴∠FEG=∠CGE﹣∠EFG=β+(110°﹣α)﹣2β=110°﹣α﹣β,
70°﹣β=110°﹣α﹣β,
解得α=40°,
∴∠AEP=40°;
(3)如图2,∵EF平分∠PEB,
∴可设∠BEF=∠PEF=α,
∵AB∥CD,
∴∠GFE=∠BEF=α,
∴四边形PGFE中,∠PGF=360°﹣∠P﹣2α,
∴∠PGC=180°﹣(360°﹣∠P﹣2α)=∠P+2α﹣180°,
∵∠EFG是△FGH的外角,
∴∠FGH=∠EFG﹣∠EHG=α﹣∠EHG,
又∵QG平分∠PGC,
∴∠PGC=2∠FGH,
即∠P+2α﹣180°=2(α﹣∠EHG),
整理可得,∠P+2∠EHG=180°.
故答案为:∠P+2∠EHG=180°.
25.解:(1)如图1,∵DE、DF分别是∠CDO、∠CDB的平分线,
∴∠CDF=∠CDB,∠CDE=∠CDO,
∴∠EDF=(∠CDB+∠CDO)=90°,
又∵DF∥AO,
∴∠AED=90°,
∴DE⊥AO;
(2)如图2,连接OC,
∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠CDB是△COD的外角,∠AEC是△COE的外角,
∴∠CDB=∠COD+∠OCD,∠AEC=∠EOC+∠ECO,
∴∠CDB+∠AEC=∠COD+∠OCD+∠EOC+∠ECO=2∠DCE;
(3)图3中,∠CDB=∠AEC+2∠DCE;图4中,∠AEC=∠CDB+2∠DCE.理由:
如图3,∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠CDB是△ODG的外角,
∴∠CDB=∠DOG+∠DGO,
∵∠DGO是△CEG的外角,
∴∠DGO=∠AEC+∠C,
∴∠CDB=∠DOG+∠AEC+∠C=∠AEC+2∠DCE;
如图4,∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠AEC是△OEH的外角,
∴∠AEC=∠DOE+∠OHE,
∵∠OHE是△CDH的外角,
∴∠OHE=∠CDB+∠C,
∴∠AEC=∠DOE+∠CDB+∠C=∠CDB+2∠DCE.
26.解:(1)如图1,∵OP∥AE,
∴∠A=∠1,
∵∠BOP=58°,OB是∠AOP的角平分线,
∴∠AOP=2∠BOP=116°
∴∠1=180°﹣116°=64°,
∴∠A=∠1=64°;
(2)如图2,
∵OP∥AE,
∴∠POD=∠ADO=39°,
∵OB平分∠AOC,
∴∠AOB=∠BOC,
∵OD平分∠COP,
∴∠COP=2∠DOP=78°,
∴∠ABO﹣∠AOB=∠COP=78°;
(3)如图3,由(1)可知,∠ABO=(180°﹣m),∠AB1O=(180°﹣∠OBB1)=∠ABO=(180°﹣m),∠AB2O=(180°﹣m),…
则∠ABnO=.
27.解:(1)如图,设FG与NE交点为H点,AB与NE的交点I,
在△HNG中,∵∠G+∠HNG+∠NHG=180°
∴∠HNG=∠AIE=∠IHM+∠IMH=(∠E+∠EMF)+∠IMH=∠E+(∠EMF+∠IMH
)=∠E+∠AME
∠NHG=∠IHM=∠E+∠EMF=∠E+∠AME
∴∠G+∠HNG+∠NHG=∠G+(∠E+∠AME)+(∠E+∠AME)=180°
(∠G+2∠E)+∠AME=180°,即90°+∠AME=180°,
∴∠AME=60°;
(2)∠JPQ的度数不改变,
∵PQ平分∠MPN,NH平分∠PNC,
∴∠JPQ=∠JPN﹣∠MPN
=(∠ENC﹣∠MPN)
=(∠AOE﹣∠MPN)
=∠AME
=30°.
28.解:∵AD∥EF,
∴∠2=∠DAC,
∵∠1=∠2,
∴∠1=∠DAC,
∴∠GD∥AC,
∴∠BAG=∠C,
∵∠BAC=80°,∠B=∠C,
∴2∠C=180°﹣∠BAC=100°,
∴∠C=50°,
∴∠BDG=50°.
29.解:(1)∵AB∥CD,∠CDE=50°,
∴∠BED=∠CDE=50°,
∵EG平分∠DEB,
∴∠DEG=25°,
∵∠F=25°,
∴∠F=∠DEG=25°,
∴BF∥EG,
∵FB⊥BD,
∴EG⊥BD;
(2)由(1)得∠FBE=∠BEG=25°,
∵∠FBD=90°,
∴∠EBD=65°,
∵AB∥CD,
∴∠CDB=115°.
30.解:(1)∵射线CD∥AB,∠C=110°,
∴∠CAB=70°,∠BAD=∠EAD,
∵∠EAD=∠EDA,
∴∠EAD=∠BAD=∠EAB.
∵AF平分∠CAE,
∴∠FAD=∠FAE+∠EAD=∠CAB=×70°=35°;
(2)不变.
∵AB∥CD,∠C=110°,
∴∠CAB=70°.
当BD向右平移时,∠EAD增大,∠CAB不变,
∵∠EAD=∠EDA,∠AEC=∠EAD+∠EDA,
∴∠ADC:∠AEC=1:2;
(3)存在.
设∠BAD=∠EAD=∠EDA=x°,
∵由(1)知∠FAD=35°,
∴∠AFC=x°+35°.
∵AB∥CD,∠ABD=110°,
∴∠BDC=70°,
∴∠ADB=70°﹣x°,
∵∠AFC=∠ADB,
∴x°+35°=70°﹣x°,解得x=17.5°,
∴∠ADB=70°﹣17.5°=52.5°.
31.证明:连接EF.
∵FG⊥AC,HE⊥AC,
∴∠FGC=∠HEC=90°.
∴FG∥HE(同位角相等,两直线平行).
∴∠3=∠4(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4,
即∠DEF=∠EFC.
∴DE∥BC(内错角相等,两直线平行).
故答案为:HE,同位角相等,两直线平行;4,两直线平行,内错角相等;∠1+∠3,DEF,内错角相等,两直线平行.
32.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠EGF=∠AEG+∠GFC;
(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点N作HT∥GN,
则∠MHT=∠N=2α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+2β,
∠CGH=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,
∵AB∥CD,
∴∠AGH+∠CGH=180°,
∴90°+α+2α+3β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
33.(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵∠BCF+∠ADE=180°.
∴∠BCF+∠B=180°.
∴CF∥AB;
(2)解:如图2,过点E作EK∥AB,
∴∠BEK=∠ABE=40°,
∵CF∥AB,
∴CF∥EK,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
(3)∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=7:13,
∴设∠EBC=7x°,则∠ECB=13x°,
∵DE∥BC,
∴∠DEB=∠EBC=7x°,∠AED=∠ECB=13x°,
∵∠AED+∠DEB+∠BEC=180°,
∴13x+7x+100=180,
解得x=4,
∴∠EBC=7x°=28°,
∵∠EBG=∠EBC+∠CBG,
∴∠CBG=∠EBG﹣∠EBC=40°﹣28°=12°.
34.(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFE=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90﹣x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
35.证明:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°
∴∠ADF=∠BCF(同角的补角相等)
∴AD∥BC(同位角相等,两直线平行)
∵BE平分∠ABC
∴∠ABC=2∠ABE(角平分线定义)
又∵∠ABC=2∠E
∴∠ABE=∠E
∴AB∥EF(内错角相等,两直线平行)
∵AD∥BC
∴∠BAD+∠ABC=180°(两直线平行,同旁内角互补)
BE平分∠ABC,AE平分∠BAD
∴∠ABE=∠ABC,∠BAF=∠BAD
∴∠ABE+∠BAF=∠ABC+∠BAD=×180°=90°
∵AB∥EF(己证)
∴∠BAF=∠F(两直线平行,内错角相等)
∠ABE=∠E
∴∠E+∠F=90°(等量代换)
36.解:(1)AD∥EF,
理由:∵∠BDA+∠CEG=180°,∠BDA+∠CDA=180°,
∴∠CEG=∠CDA,
∴AD∥EF;
(2)AD平分∠BAC,
理由:∵∠EDH=∠C,
∴DH∥AC,
∴∠H=∠EGC,
∵∠F=∠H,
∴∠F=∠EGC,
∵AD∥EF,
∴∠BAD=∠F,∠CAD=∠EGC,
∴∠BAD=∠CAD,
∴AD平分∠BAC.
37.(1)解:∵AD∥BE,
∴∠CAD=∠3,
∵∠2+∠CAE=∠CAD,∠3=80°,
∴∠2+∠CAE=80°,
∵∠2=30°,
∴∠CAE=50°;
(2)证明:∵∠2+∠CAE=∠CAD=∠3,
∠1=∠2,∠3=∠4,
∴∠1+∠CAE=∠4,
即∠BAE=∠4,
∴AB∥DC.
38.解:(1)证明:∵∠BDA+∠CEG=180°,∠BDA+∠ADC=180°.
∴∠ADC=∠CEG,
∴AD∥EF;
(2)∠BAD和∠CAD相等,理由如下:
∵∠EDH=∠C,
∴DH∥AC,
∴∠H=∠CGH,
∵∠CGH=∠AGF,
∴∠H=∠AGF,
∵∠F=∠H,
∴∠F=∠AGF,
∵AD∥EF,
∴∠BAD=∠F,∠CAD=∠AGF,
∴∠BAD=∠CAD;
(3)∵FH⊥BC,
∴∠CEG=90°,
∵∠C=30°,
∴∠CGE=90°﹣30°=60°,
∴∠F=∠AGF=∠CGE=60°.
39.(1)证明:∵∠A+∠3=180°,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠ABD=180°,
∴∠D+∠CBD+∠CBA=180°,
∵∠D=80°,∠CBD=70°,
∴∠CBA=180°﹣∠D﹣∠CBD
=180°﹣80°﹣70°
=30°.
40.解:(1)证明:∵FG∥AE,
∴∠FGC=∠2,
∵∠1=∠2,
∴∠1=∠FGC,
∴AB∥CD;
(2)∵AB∥CD,
∴∠ABC+∠D=180°,
∵∠D=112°,
∴∠ABD=180°﹣112°=68°,
∵BC平分∠ABD,
∴∠ABC=ABD=34°,
∵AB∥CD,
∴∠C=∠ABC=34°.
所以∠C的度数为34°
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
