2021年春苏科版七年级数学下册7.2探索平行线的性质 平行线的性质自主学习同步训练1(Word版 附答案)
文档属性
| 名称 | 2021年春苏科版七年级数学下册7.2探索平行线的性质 平行线的性质自主学习同步训练1(Word版 附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 167.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 19:26:42 | ||
图片预览



文档简介
2021年苏科新版七年级数学下册7.2平行线的性质自主学习同步训练1(附答案)
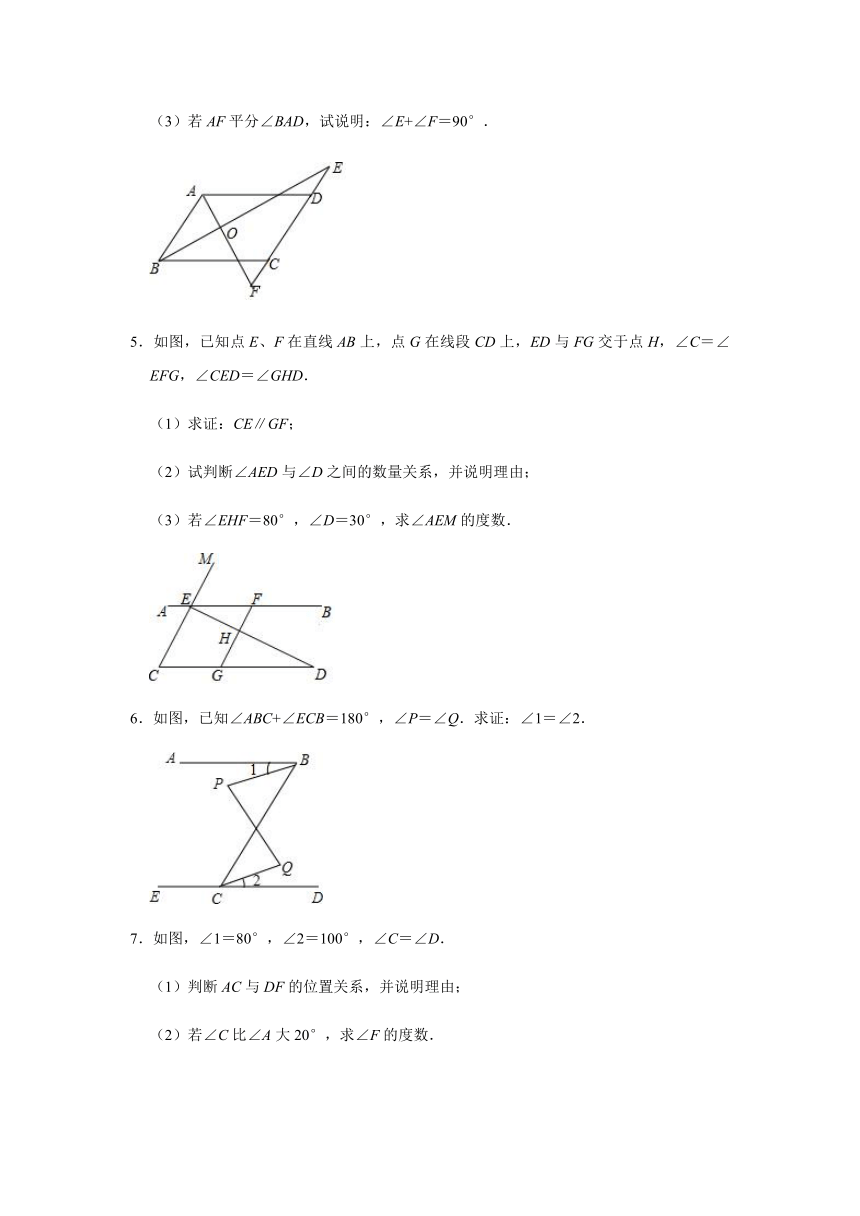
1.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系?加以证明;
(2)若∠CEF=70°,求∠ACB的度数.
2.如图,AB∥DG,AD∥EF.
(1)试说明:∠1+∠2=180°;
(2)若DG是∠ADC的平分线,∠2=138°,求∠B的度数.
3.如图,AB∥CD,∠ADC=∠ABC.求证:∠E=∠F.
4.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
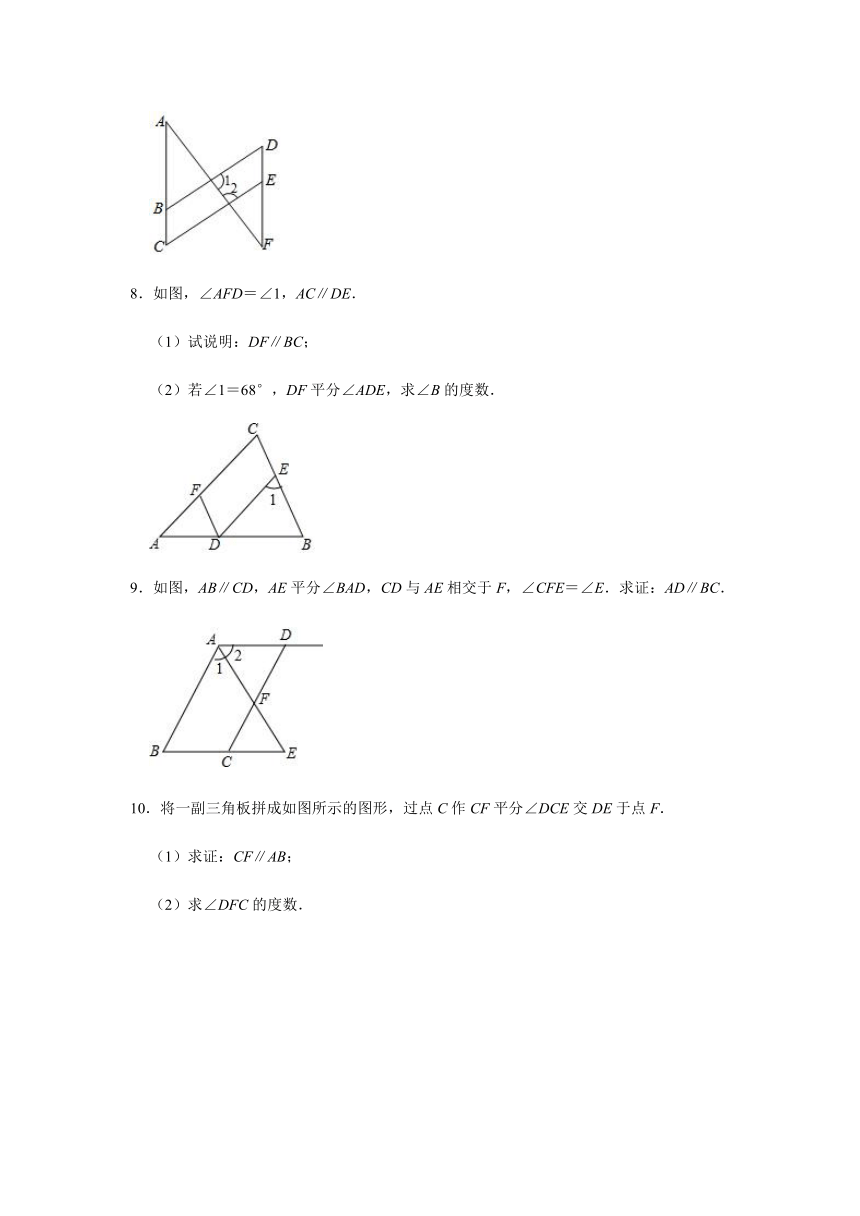
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
5.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
6.如图,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
7.如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断AC与DF的位置关系,并说明理由;
(2)若∠C比∠A大20°,求∠F的度数.
8.如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
9.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.
10.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
11.如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
12.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2
(1)求证:AB∥CD
(2)若∠D=∠3+50°,∠CBD=70°,求∠C的度数.
13.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求∠3的度数.
14.如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.
15.如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
16.如图,AE∥CF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若AD平分∠BDF,试说明BC平分∠DBE.
17.已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.
①求证:∠ABC=∠ADC;
②求∠CED的度数.
18.如图,已知BC∥GE,AF∥DE,∠1=50°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
19.如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
20.已知:如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB,
(1)求证:CE∥DF;
(2)若∠DCE=130°,求∠DEF的度数.
21.如图,AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE.
22.已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
23.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
24.如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
25.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
参考答案
1.解:(1)EF和AB的关系为平行关系.理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC﹣∠CBF=50°,
∵∠EFB=130°,
∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵∠CEF=70°,
∴∠ECD=110°,
∵∠DCB=70°,
∴∠ACB=∠ECD﹣∠DCB,
∴∠ACB=40°.
2.解:(1)∵AD∥EF,
∴∠BAD+∠2=180°,
∵AB∥DG,
∴∠BAD=∠1,
∴∠1+∠2=180°.
(2)∵∠1+∠2=180°且∠2=138°,
∴∠1=42°,
∵DG是∠ADC的平分线,
∴∠CDG=∠1=42°,
∵AB∥DG,
∴∠B=∠CDG=42°.
3.证明:∵AB∥CD,
∴∠ABC=∠DCF.
又∵∠ADC=∠ABC
∴∠ADC=∠DCF.
∴DE∥BF.
∴∠E=∠F.
4.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
5.解:(1)∵∠CED=∠GHD,
∴CE∥GF;
(2)∠AED+∠D=180°;
理由:∵CE∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=80°+30°=110°,
又∵CE∥GF,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.
6.证明:∵∠ABC+∠ECB=180°,
∴AB∥DE,
∴∠ABC=∠BCD,
∵∠P=∠Q,
∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
7.解:(1)AC∥DF,理由如下:
∵∠1=80°,∠2=100°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠ABD=∠C,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF;
(2)∵AC∥DF,
∴∠A=∠F,∠ABD=∠D,
∵∠C=∠D,∠1=80°,
∴∠A+∠ABD=180°﹣80°=100°,
即∠A+∠C=100°,
∵∠C比∠A大20°,
∴∠A=40°,
∴∠F=40°.
8.解:(1)∵AC∥DE,
∴∠C=∠1,
∵∠AFD=∠1,
∴∠C=∠AFD,
∴DF∥BC.
(2)∵∠1=68°,DF∥BC,
∴∠EDF=∠1=68°,
∵DF平分∠ADE,
∴∠ADF=∠EDF=68°,
∵DF∥BC,
∴∠B=∠ADF=68°.
9.证明:∵AE平分∠BAD,
∴∠1=∠2,
∵AB∥CD,∠CFE=∠E,
∴∠1=∠CFE=∠E,
∴∠2=∠E,
∴AD∥BC.
10.(1)证明:由题意知,△ACB是等腰直角三角形,且∠ACB=∠DCB=90°,
∴∠B=45°.
∵CF平分∠DCE,
∴∠DCF=∠ECF=45°,
∴∠B=∠ECF,
∴CF∥AB.
(2)由三角板知,∠E=60°,
由(1)知,∠ECF=45°,
∵∠DFC=∠ECF+∠E,
∴∠DFC=45°+60°=105°.
11.证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AB∥EF,
∴∠A=∠F.
12.(1)证明:∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNM=90°,
∴AE∥FG,
∴∠A=∠2;
又∵∠2=∠1,
∴∠A=∠1,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠CBD+∠3=180°,
∵∠D=∠3+50°,∠CBD=70°,
∴∠3=30°,
∵AB∥CD,
∴∠C=∠3=30°.
13.(1)证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠BCD.
又∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC.
(2)解:在Rt△BEF中,∠B=54°,
∴∠2=180°﹣90°﹣54°=36°,
∴∠BCD=∠2=36°.
又∵BC∥DG,
∴∠3=∠ACB=∠ACD+∠BCD=35°+36°=71°.
14.解:过点D作DG∥b,
∵a∥b,且DE⊥b,
∴DG∥a,
∴∠1=∠CDG=25°,∠GDE=∠3=90°
∴∠2=∠CDG+∠GDE=25°+90°=115°.
15.(1)解:
∵AP平分∠BAC,
∴∠CAP=∠BAP=α,
∵∠P=90°,
∴∠ACP=90°﹣∠CAP=90°﹣α;
(2)证明:
由(1)可知∠ACP=90°﹣α,
∵CP平分∠ACD,
∴∠ACD=2∠ACP=180°﹣2α,
又∠BAC=2∠BAP=2α,
∴∠ACD+∠BAC=180°,
∴AB∥CD;
(3)证明:
∵AP∥CF,
∴∠ECF=∠CAP=α,
由(2)可知AB∥CD,
∴∠ECD=∠CAB=2α,
∴∠DCF=∠ECD﹣∠ECF=α,
∴∠ECF=∠DCF,
∴CF平分∠DCE.
16.解:(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°﹣∠BDC=180°﹣35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,
∴∠A+∠ADC=180°,
又∵∠A=∠C,
∴∠C+∠ADC=180°,
∴BC∥AD.
(3)∵AE∥CF,
∴∠BDF=∠DBE.
∵BC∥AD,
∴∠ADB=∠DBC.
∵AD平分∠BDF,
∴∠ADB=∠BDF,
∴∠DBC=∠EBD.
∴BC平分∠DBE.
17.(1)证明:∵AE平分∠BAD,
∴∠BAE=∠EAD,
∵AD∥BC,
∴∠AEB=∠EAD,
∴∠BAE=∠BEA;
(2)①证明:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC;
②解:∵∠ADE=3∠CDE,设∠CDE=x°,
∴∠ADE=3x°,∠ADC=2x°,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴∠DAB=180°﹣2x°,
∵∠DAE=∠BAE=∠BEA=90°﹣x°,
又∵AD∥BC,
∴∠BED+∠ADE=180°,
∵∠AED=60°,
即90﹣x+60+3x=180,
∴∠CDE=x°=15°,∠ADE=45°,
∵AD∥BC,
∴∠CED=180°﹣∠ADE=135°.
18.解:(1)∵BC∥EG,
∴∠E=∠1=50°.
∵AF∥DE,
∴∠AFG=∠E=50°;
(2)作AM∥BC,
∵BC∥EG,
∴AM∥EG,
∴∠FAM=∠AFG=50°.
∵AM∥BC,
∴∠QAM=∠Q=15°,
∴∠FAQ=∠FAM+∠QAM=65°.
∵AQ平分∠FAC,
∴∠QAC=∠FA
Q=65°,
∴∠M
AC=∠QAC+∠QAM=80°.
∵AM∥BC,
∴∠ACB=∠MAC=80°.
19.解:(1)∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°;
(2)∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG.
20.(1)证明:∵∠1+∠2=180°,C,D是直线AB上两点,
∴∠1+∠DCE=180°,
∴∠2=∠DCE,
∴CE∥DF;
(2)解:∵CE∥DF,∠DCE=130°,
∴∠CDF=180°﹣∠DCE=180°﹣130°=50°,
∵DE平分∠CDF,
∴∠CDE=∠CDF=25°,
∵EF∥AB,
∴∠DEF=∠CDE=25°.
21.证明:∵AB∥CD,
∴∠1=∠6,
∵∠1=∠2,∠3=∠4,
∴∠3+∠6=∠4+∠2,
∵∠4=∠5,
∴∠3+∠6=∠2+∠5,
∵∠2+∠5+∠D=180°,
∴∠3+∠6+∠D=180°,
即∠BCD+∠D=180°,
∴AD∥BE.
22.解:BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF(同位角相等,两直线平行),
∴∠1=∠3,
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE,
∵DE⊥AC,
∴BF⊥AC.
23.解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°,
∴∠DCF=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.
24.证明:∵CF⊥AB,ED⊥AB,
∴DE∥FC(垂直于同一条直线的两条直线互相平行),
∴∠1=∠BCF(两直线平行,同位角相等);
又∵∠2=∠1(已知),
∴∠BCF=∠2(等量代换),
∴FG∥BC(内错角相等,两直线平行).
25.解:∵DE∥BC,∠AED=80°,
∴∠ACB=∠AED=80°(两直线平行,同位角相等),
∵CD平分∠ACB,
∴∠BCD=∠ACB=40°,
∵DE∥BC,
∴∠EDC=∠BCD=40°(两直线平行,内错角相等)
1.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系?加以证明;
(2)若∠CEF=70°,求∠ACB的度数.
2.如图,AB∥DG,AD∥EF.
(1)试说明:∠1+∠2=180°;
(2)若DG是∠ADC的平分线,∠2=138°,求∠B的度数.
3.如图,AB∥CD,∠ADC=∠ABC.求证:∠E=∠F.
4.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
5.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
6.如图,已知∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
7.如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断AC与DF的位置关系,并说明理由;
(2)若∠C比∠A大20°,求∠F的度数.
8.如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
9.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.
10.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
11.如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
12.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2
(1)求证:AB∥CD
(2)若∠D=∠3+50°,∠CBD=70°,求∠C的度数.
13.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求∠3的度数.
14.如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,求∠2的度数.
15.如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
16.如图,AE∥CF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若AD平分∠BDF,试说明BC平分∠DBE.
17.已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.
①求证:∠ABC=∠ADC;
②求∠CED的度数.
18.如图,已知BC∥GE,AF∥DE,∠1=50°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
19.如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
20.已知:如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB,
(1)求证:CE∥DF;
(2)若∠DCE=130°,求∠DEF的度数.
21.如图,AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE.
22.已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
23.如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
24.如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
25.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
参考答案
1.解:(1)EF和AB的关系为平行关系.理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC﹣∠CBF=50°,
∵∠EFB=130°,
∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵∠CEF=70°,
∴∠ECD=110°,
∵∠DCB=70°,
∴∠ACB=∠ECD﹣∠DCB,
∴∠ACB=40°.
2.解:(1)∵AD∥EF,
∴∠BAD+∠2=180°,
∵AB∥DG,
∴∠BAD=∠1,
∴∠1+∠2=180°.
(2)∵∠1+∠2=180°且∠2=138°,
∴∠1=42°,
∵DG是∠ADC的平分线,
∴∠CDG=∠1=42°,
∵AB∥DG,
∴∠B=∠CDG=42°.
3.证明:∵AB∥CD,
∴∠ABC=∠DCF.
又∵∠ADC=∠ABC
∴∠ADC=∠DCF.
∴DE∥BF.
∴∠E=∠F.
4.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
5.解:(1)∵∠CED=∠GHD,
∴CE∥GF;
(2)∠AED+∠D=180°;
理由:∵CE∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=80°+30°=110°,
又∵CE∥GF,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.
6.证明:∵∠ABC+∠ECB=180°,
∴AB∥DE,
∴∠ABC=∠BCD,
∵∠P=∠Q,
∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
7.解:(1)AC∥DF,理由如下:
∵∠1=80°,∠2=100°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠ABD=∠C,
∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF;
(2)∵AC∥DF,
∴∠A=∠F,∠ABD=∠D,
∵∠C=∠D,∠1=80°,
∴∠A+∠ABD=180°﹣80°=100°,
即∠A+∠C=100°,
∵∠C比∠A大20°,
∴∠A=40°,
∴∠F=40°.
8.解:(1)∵AC∥DE,
∴∠C=∠1,
∵∠AFD=∠1,
∴∠C=∠AFD,
∴DF∥BC.
(2)∵∠1=68°,DF∥BC,
∴∠EDF=∠1=68°,
∵DF平分∠ADE,
∴∠ADF=∠EDF=68°,
∵DF∥BC,
∴∠B=∠ADF=68°.
9.证明:∵AE平分∠BAD,
∴∠1=∠2,
∵AB∥CD,∠CFE=∠E,
∴∠1=∠CFE=∠E,
∴∠2=∠E,
∴AD∥BC.
10.(1)证明:由题意知,△ACB是等腰直角三角形,且∠ACB=∠DCB=90°,
∴∠B=45°.
∵CF平分∠DCE,
∴∠DCF=∠ECF=45°,
∴∠B=∠ECF,
∴CF∥AB.
(2)由三角板知,∠E=60°,
由(1)知,∠ECF=45°,
∵∠DFC=∠ECF+∠E,
∴∠DFC=45°+60°=105°.
11.证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AB∥EF,
∴∠A=∠F.
12.(1)证明:∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNM=90°,
∴AE∥FG,
∴∠A=∠2;
又∵∠2=∠1,
∴∠A=∠1,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠CBD+∠3=180°,
∵∠D=∠3+50°,∠CBD=70°,
∴∠3=30°,
∵AB∥CD,
∴∠C=∠3=30°.
13.(1)证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠BCD.
又∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC.
(2)解:在Rt△BEF中,∠B=54°,
∴∠2=180°﹣90°﹣54°=36°,
∴∠BCD=∠2=36°.
又∵BC∥DG,
∴∠3=∠ACB=∠ACD+∠BCD=35°+36°=71°.
14.解:过点D作DG∥b,
∵a∥b,且DE⊥b,
∴DG∥a,
∴∠1=∠CDG=25°,∠GDE=∠3=90°
∴∠2=∠CDG+∠GDE=25°+90°=115°.
15.(1)解:
∵AP平分∠BAC,
∴∠CAP=∠BAP=α,
∵∠P=90°,
∴∠ACP=90°﹣∠CAP=90°﹣α;
(2)证明:
由(1)可知∠ACP=90°﹣α,
∵CP平分∠ACD,
∴∠ACD=2∠ACP=180°﹣2α,
又∠BAC=2∠BAP=2α,
∴∠ACD+∠BAC=180°,
∴AB∥CD;
(3)证明:
∵AP∥CF,
∴∠ECF=∠CAP=α,
由(2)可知AB∥CD,
∴∠ECD=∠CAB=2α,
∴∠DCF=∠ECD﹣∠ECF=α,
∴∠ECF=∠DCF,
∴CF平分∠DCE.
16.解:(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°﹣∠BDC=180°﹣35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,
∴∠A+∠ADC=180°,
又∵∠A=∠C,
∴∠C+∠ADC=180°,
∴BC∥AD.
(3)∵AE∥CF,
∴∠BDF=∠DBE.
∵BC∥AD,
∴∠ADB=∠DBC.
∵AD平分∠BDF,
∴∠ADB=∠BDF,
∴∠DBC=∠EBD.
∴BC平分∠DBE.
17.(1)证明:∵AE平分∠BAD,
∴∠BAE=∠EAD,
∵AD∥BC,
∴∠AEB=∠EAD,
∴∠BAE=∠BEA;
(2)①证明:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC;
②解:∵∠ADE=3∠CDE,设∠CDE=x°,
∴∠ADE=3x°,∠ADC=2x°,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴∠DAB=180°﹣2x°,
∵∠DAE=∠BAE=∠BEA=90°﹣x°,
又∵AD∥BC,
∴∠BED+∠ADE=180°,
∵∠AED=60°,
即90﹣x+60+3x=180,
∴∠CDE=x°=15°,∠ADE=45°,
∵AD∥BC,
∴∠CED=180°﹣∠ADE=135°.
18.解:(1)∵BC∥EG,
∴∠E=∠1=50°.
∵AF∥DE,
∴∠AFG=∠E=50°;
(2)作AM∥BC,
∵BC∥EG,
∴AM∥EG,
∴∠FAM=∠AFG=50°.
∵AM∥BC,
∴∠QAM=∠Q=15°,
∴∠FAQ=∠FAM+∠QAM=65°.
∵AQ平分∠FAC,
∴∠QAC=∠FA
Q=65°,
∴∠M
AC=∠QAC+∠QAM=80°.
∵AM∥BC,
∴∠ACB=∠MAC=80°.
19.解:(1)∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°;
(2)∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG.
20.(1)证明:∵∠1+∠2=180°,C,D是直线AB上两点,
∴∠1+∠DCE=180°,
∴∠2=∠DCE,
∴CE∥DF;
(2)解:∵CE∥DF,∠DCE=130°,
∴∠CDF=180°﹣∠DCE=180°﹣130°=50°,
∵DE平分∠CDF,
∴∠CDE=∠CDF=25°,
∵EF∥AB,
∴∠DEF=∠CDE=25°.
21.证明:∵AB∥CD,
∴∠1=∠6,
∵∠1=∠2,∠3=∠4,
∴∠3+∠6=∠4+∠2,
∵∠4=∠5,
∴∠3+∠6=∠2+∠5,
∵∠2+∠5+∠D=180°,
∴∠3+∠6+∠D=180°,
即∠BCD+∠D=180°,
∴AD∥BE.
22.解:BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF(同位角相等,两直线平行),
∴∠1=∠3,
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE,
∵DE⊥AC,
∴BF⊥AC.
23.解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°,
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°,
∴∠DCF=50°,
∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.
24.证明:∵CF⊥AB,ED⊥AB,
∴DE∥FC(垂直于同一条直线的两条直线互相平行),
∴∠1=∠BCF(两直线平行,同位角相等);
又∵∠2=∠1(已知),
∴∠BCF=∠2(等量代换),
∴FG∥BC(内错角相等,两直线平行).
25.解:∵DE∥BC,∠AED=80°,
∴∠ACB=∠AED=80°(两直线平行,同位角相等),
∵CD平分∠ACB,
∴∠BCD=∠ACB=40°,
∵DE∥BC,
∴∠EDC=∠BCD=40°(两直线平行,内错角相等)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
